LM算法在二階過阻尼系統(tǒng)參數(shù)估計(jì)中的應(yīng)用

Application of LM Algorithm in Parameter Estimation for Second-order Over-damped System

李敏花　柏　猛　呂英俊

(山東科技大學(xué)電氣信息系，山東 濟(jì)南　250031)

LM算法在二階過阻尼系統(tǒng)參數(shù)估計(jì)中的應(yīng)用

Application of LM Algorithm in Parameter Estimation for Second-order Over-damped System

李敏花柏猛呂英俊

(山東科技大學(xué)電氣信息系，山東 濟(jì)南250031)

摘要：針對(duì)二階過阻尼系統(tǒng)傳遞函數(shù)的參數(shù)辨識(shí)問題，提出一種根據(jù)二階過阻尼系統(tǒng)階躍響應(yīng)估計(jì)系統(tǒng)傳遞函數(shù)未知參數(shù)的新方法。該方法首先求解出二階過阻尼系統(tǒng)的階躍響應(yīng)表達(dá)式，然后定義模型輸出與觀測(cè)數(shù)據(jù)的差值作為代價(jià)函數(shù)，將參數(shù)估計(jì)問題轉(zhuǎn)換為非線性最小二乘問題。通過采用Levenberg-Marquarat算法極小化代價(jià)函數(shù)，估計(jì)出系統(tǒng)未知參數(shù)。為確定參數(shù)估計(jì)的初值，給出采用兩點(diǎn)法的參數(shù)初值估計(jì)方法。仿真結(jié)果表明，在含有觀測(cè)噪聲的情況下，提出的方法能有效解決過阻尼二階系統(tǒng)未知參數(shù)的估計(jì)問題。

關(guān)鍵詞：二階過阻尼系統(tǒng)傳遞函數(shù)參數(shù)估計(jì)階躍響應(yīng)非線性最小二乘Levenberg-Marquarat算法觀測(cè)噪聲

Abstract：Aiming at the problem of parameter identification for transfer function of two order over damping system, a novel method for estimating unknown parameters in transfer function of the second order over-damped system in accordance with its step response is proposed. With this method, firstly, the expression of the step response of the second order over-damped system is solved, then defining the difference between the model output and observed data as the cost function, the issue of parameter estimation is converted into a nonlinear least square topic. The cost function is minimized through using Levenberg-Marquarat (L-M) algorithm, to estimate unknown parameters of the system. In order to determine that initial value for parameter estimation, the estimation method of initial value two-point method is given. The results of simulation demonstrate that the method proposed can effectively solve the problem for unknown parameter estimation of such system under observation noises exist.

Keywords：Second-order over-damped systemTransfer functionParameter estimationStep responseNonlinear least square

Levenberg-Marquarat algorithmObservation noise

0引言

在基于模型的控制系統(tǒng)設(shè)計(jì)中，建立系統(tǒng)動(dòng)態(tài)模型是控制器設(shè)計(jì)的前提,模型的精確程度直接影響所設(shè)計(jì)控制系統(tǒng)的性能。在眾多的系統(tǒng)模型中，二階系統(tǒng)模型被廣泛應(yīng)用于慣導(dǎo)系統(tǒng)[1]、化工過程、機(jī)電設(shè)備等系統(tǒng)的建模,在實(shí)際應(yīng)用中，獲得這些系統(tǒng)模型最有效的途徑是系統(tǒng)辨識(shí)。雖然近年來在采用系統(tǒng)辨識(shí)方法獲取二階系統(tǒng)傳遞函數(shù)的研究方面已取得較大進(jìn)展[1-4]，但對(duì)一些化工過程和無法實(shí)現(xiàn)頻繁啟動(dòng)的機(jī)電設(shè)備，現(xiàn)實(shí)的建模方法依然是通過系統(tǒng)階躍響應(yīng)數(shù)據(jù)獲取系統(tǒng)模型。目前，由階躍響應(yīng)曲線辨識(shí)二階系統(tǒng)傳遞函數(shù)參數(shù)的經(jīng)典方法主要有兩點(diǎn)法、相良節(jié)夫法、半對(duì)數(shù)法和面積法等[2]。但這些方法的精度受觀測(cè)噪聲的影響較大,對(duì)此，本文提出一種基于數(shù)據(jù)擬合的二階過阻尼系統(tǒng)參數(shù)辨識(shí)方法。該方法通過將二階系統(tǒng)的參數(shù)辨識(shí)問題轉(zhuǎn)換為階躍響應(yīng)數(shù)據(jù)的擬合問題，采用非線性最小二乘方法解決含有觀測(cè)噪聲情況下二階過阻尼系統(tǒng)的參數(shù)辨識(shí)問題。

1非線性最小二乘參數(shù)估計(jì)方法

1.1　算法原理

在不考慮時(shí)間滯后的情況下，典型二階過阻尼系統(tǒng)傳遞函數(shù)可表示為：

(1)

式中：T1和T2為時(shí)間常數(shù)，且T1≥T2。在零初始狀態(tài)下，二階過阻尼系統(tǒng)的單位階躍響應(yīng)可表示為：

(2)

假設(shè)在ti時(shí)刻，系統(tǒng)階躍響應(yīng)y(ti)的觀測(cè)值為z(ti)，且有：

z(ti)=y(ti)+v(ti)

(3)

式中：v(ti)為觀測(cè)噪聲，i=1，2，…，N。

令z(i)=z(ti)、y(i)=y(ti)、θ=[T1,T2]T，則二階系統(tǒng)未知參數(shù)θ的估計(jì)問題可轉(zhuǎn)化為如下函數(shù)的極小化問題：

(4)

式中：J(θ)為代價(jià)函數(shù)。

(5)

顯然，代價(jià)函數(shù)J(θ)的極小化問題是典型的非線性最小二乘問題。令fi(θ)=z(i)-y(i)，則式(5)可表示為：

(6)

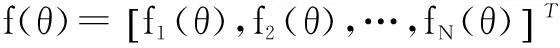
假設(shè)f(θ)具有連續(xù)的二階偏導(dǎo)數(shù)，則f(θ)在θ附近的Taylor展開可表示為：

f(θ+Δθ)=f(θ)+s(θ)Δθ+O(‖Δθ‖2)≈

f(θ)+s(θ)Δθ=l(Δθ)

(7)

式中：s(θ)為Jacobian矩陣。

(8)

將式(7)代入式(6)，可得：

(9)

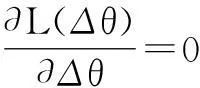
sT(θ)s(θ)Δθ=-sT(θ)f(θ)

(10)

當(dāng)sT(θ)s(θ)為正定矩陣時(shí)，求解式(10)可得經(jīng)典Guass-Newton方法迭代步長(zhǎng)：

(11)

當(dāng)s(θ)Ts(θ)為半正定矩陣時(shí)，為使式(10)有解，采用阻尼Guass-Newton方法可得：

(12)

式中：μ>0為阻尼系數(shù)。

一般情況下，對(duì)于算法的每一步迭代，希望在保證算法函數(shù)值有一定下降量的情況下，步長(zhǎng)盡可能大，以便盡快接近最優(yōu)點(diǎn)。因此，μ的取值非常關(guān)鍵。為解決μ的取值問題，本文采用Levenberg-Marquarat(LM)算法解決代價(jià)函數(shù)的極小化問題。LM算法結(jié)合了Guass-Newton算法和梯度下降法的優(yōu)點(diǎn)[5]，可較好地解決非線性最小二乘問題，被廣泛應(yīng)用于各類最優(yōu)化問題的求解[6-9]。在LM算法中，(k+1)次迭代的μ值取決于k次迭代和(k-1)次迭代J(θk)和J(θk-1)的值，即：

(13)

式中：λ>1為增長(zhǎng)因子，一般取λ=2或10。

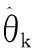
(14)

由上述參數(shù)迭代過程可見，采用式(14)估計(jì)二階系統(tǒng)未知參數(shù)時(shí)，需要設(shè)置參數(shù)初值。由于非線性最小二乘法為局部收斂，參數(shù)初值會(huì)直接影響算法的收斂，因此有必要考慮參數(shù)初值的估計(jì)問題[5]。

1.2　參數(shù)初值估計(jì)

為確定待辨識(shí)參數(shù)初值，本文采用兩點(diǎn)法計(jì)算二階系統(tǒng)參數(shù)[10]。該方法選取系統(tǒng)階躍響應(yīng)(2)中的兩個(gè)典型點(diǎn)，通過聯(lián)立方程組計(jì)算T1和T2的值。

對(duì)于二階過阻尼系統(tǒng)單位階躍響應(yīng)曲線，一般取y(t1)=0.4和y(t2)=0.8兩個(gè)點(diǎn)作為典型點(diǎn)。將這兩點(diǎn)代入式(2)，可得方程組：

(15)

該方程組的近似解為：

(16)

通過求解上式可得T1和T2的估計(jì)值。在求解過程中，對(duì)于二階系統(tǒng)，t1和t2應(yīng)滿足關(guān)系[10]：

(17)

綜上所述，本文提出的采用LM算法對(duì)二階過阻尼系統(tǒng)進(jìn)行參數(shù)辨識(shí)的方法步驟如下。

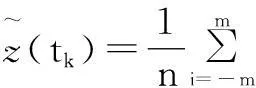
(2) 參數(shù)初值估計(jì)。取z2(tk)在0.4和0.8位置附近滿足式(17)的時(shí)間t1和t2，代入式(16)，求出T1和T2作為參數(shù)θ的初值，即θ0=[T1,T2]T。

(3) 設(shè)置阻尼系數(shù)初值μ0、增長(zhǎng)因子λ>1和迭代次數(shù)kmax。其中，本文取λ=10。

(4) 分別采用式(8)和式(12)計(jì)算sk(θ)和Δθk。

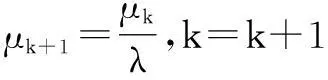
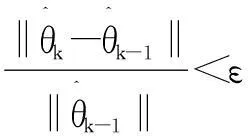
2仿真結(jié)果與分析

為檢驗(yàn)本文所提出二階過阻尼系統(tǒng)參數(shù)辨識(shí)方法的有效性，對(duì)以下典型二階過阻尼系統(tǒng)進(jìn)行參數(shù)辨識(shí)。

(1) 直流電機(jī)模型參數(shù)辨識(shí)

直流電動(dòng)機(jī)的數(shù)學(xué)模型可表示[11]：

(18)

式中：Tm和Tl分別為機(jī)電時(shí)間常數(shù)和電磁時(shí)間常數(shù)；Ce為直流電機(jī)在額定磁通下的電動(dòng)勢(shì)系數(shù)。試驗(yàn)中，模型取Ce=0.192 5，Tm=0.075，Tl=0.017，迭代次數(shù)kmax=20。參數(shù)辨識(shí)結(jié)果如表1和圖1所示。其中，表1為根據(jù)歸一化后直流電機(jī)階躍響應(yīng)得到的參數(shù)辨識(shí)結(jié)果。圖1為根據(jù)含有觀測(cè)噪聲數(shù)據(jù)辨識(shí)得到的系統(tǒng)模型與真實(shí)模型階躍響應(yīng)的比較結(jié)果。

表1　參數(shù)辨識(shí)結(jié)果

由試驗(yàn)結(jié)果可見，當(dāng)無觀測(cè)噪聲時(shí)，采用直流電機(jī)階躍響應(yīng)數(shù)據(jù)可準(zhǔn)確辨識(shí)出電機(jī)電磁時(shí)間常數(shù)和機(jī)電時(shí)間常數(shù)。當(dāng)觀測(cè)數(shù)據(jù)含有噪聲時(shí)，本文提出的算法依然可以較好地估計(jì)出電機(jī)時(shí)間常數(shù)，具有較高的參數(shù)估計(jì)精度。

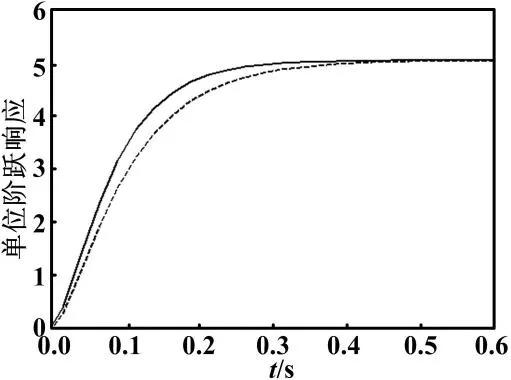
圖1　直流電機(jī)單位階躍響應(yīng)

(2) 雙慣性系統(tǒng)參數(shù)辨識(shí)

試驗(yàn)采用式(1)所示的雙慣性系統(tǒng)作為二階過阻尼系統(tǒng)。試驗(yàn)中，取T1=11，T2=3，kmax=20。采用單位階躍響應(yīng)數(shù)據(jù)得到的參數(shù)估計(jì)結(jié)果如表2所示，辨識(shí)模型與真實(shí)模型階躍響應(yīng)的比較結(jié)果如圖2所示。

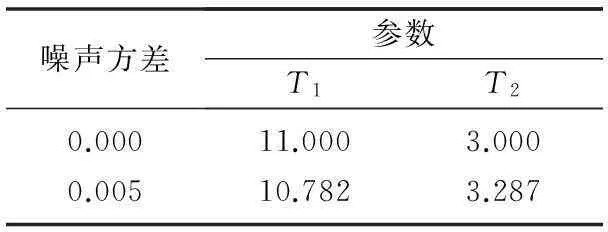
表2　參數(shù)估計(jì)結(jié)果

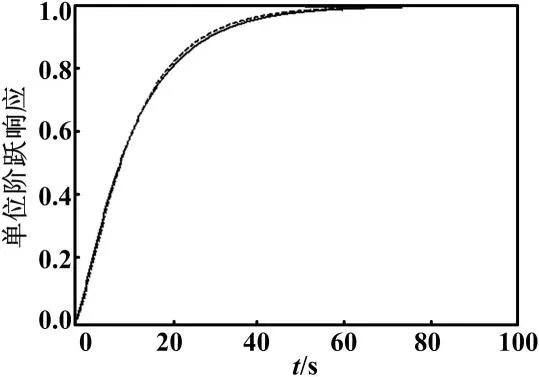
圖2　雙慣性系統(tǒng)單位階躍響應(yīng)

由試驗(yàn)結(jié)果表2和圖2可見，采用本文提出的方法可有效估計(jì)出具有較大時(shí)間常數(shù)的過阻尼系統(tǒng)參數(shù)。

雖然在含有觀測(cè)噪聲時(shí)系統(tǒng)參數(shù)的估計(jì)精度略低于無觀測(cè)噪聲時(shí)的情況，但辨識(shí)得到的系統(tǒng)模型依然具有較好的階躍響應(yīng)擬合精度。綜上所述，本文提出的方法可根據(jù)系統(tǒng)單位階躍響應(yīng)有效估計(jì)出二階過阻尼系統(tǒng)參數(shù)，適用于工業(yè)系統(tǒng)建模。

3結(jié)束語(yǔ)

本文提出的參數(shù)辨識(shí)方法是將二階系統(tǒng)參數(shù)辨識(shí)問題轉(zhuǎn)換為系統(tǒng)階躍響應(yīng)數(shù)據(jù)的非線性函數(shù)擬合問題，通過采用LM算法可有效解決參數(shù)估計(jì)中的非線性最小二乘問題。該方法適用于過程控制系統(tǒng)或無法實(shí)現(xiàn)頻繁啟動(dòng)的控制系統(tǒng)的模型辨識(shí)。由算法推導(dǎo)過程可見，該方法同樣適用于一階和二階欠阻尼系統(tǒng)的參數(shù)估計(jì)問題。在給定參數(shù)初值的情況下，該方法同樣適用于多變量系統(tǒng)的參數(shù)辨識(shí)問題。另外，提出的方法實(shí)現(xiàn)簡(jiǎn)單，適用性強(qiáng)，便于工程應(yīng)用。

參考文獻(xiàn)

[1] 胡鋼墩,李發(fā)澤.慣性系統(tǒng)的時(shí)域在線辨識(shí)[J].控制與決策,2010,25(1):133-136.

[2] 嚴(yán)德昆.二階過阻尼系統(tǒng)傳遞函數(shù)辨識(shí)的新方法[J].控制理論與應(yīng)用,2001,18(4):638-640.

[3] Bajarangbali,Somanath M.Relay based identification of systems[J].International Journal of Scientific & Engineering Research,2012,3(6):1-4.

[4] Soltesz K,Hagglund T,Astrom K J.Transfer function parameter identification by modified relay feedback[C]//Proceedings of the American Control Conference,2010:2164-2169.

[5] 張光澄,王文娟,韓會(huì)磊.非線性最優(yōu)化計(jì)算方法[M].北京:高等教育出版社,2005:146-168.

[6] Fan J.The modified Levenberg-Marquardt method for nonlinear equations with cubic convergence[J].Mathematics of Computation,2012,81(277):447-466.

[7] Sugihara T.Solvability-unconcerned inverse kinematics by the Levenberg-Marquardt method[J].IEEE Transactions on Robotics,2011,27(5):984-991.

[8] Chan K Y,Dillon T S,Singh J,et al.Neural-network-based models for short-term traffic flow forecasting using a hybrid exponential smoothing and Levenberg-Marquardt algorithm[J].IEEE Transactions on Intelligent Transportation Systems,2012,13(2):644-654.

[9] Kleefeld A,Reiβel M.The Levenberg-Marquardt method applied to a parameter estimation problem arising from electrical resistivity tomography[J].Applied Mathematics and Computation,2011,217(9):4490-4501.

[10]黃德先,王京春,金以慧.過程控制系統(tǒng)[M].北京:清華大學(xué)出版社,2011:39-44.

[11]阮毅,陳伯時(shí).電力拖動(dòng)自動(dòng)控制系統(tǒng)-運(yùn)動(dòng)控制系統(tǒng)[M].4版.北京:機(jī)械工業(yè)出版社,2010:26-29.

中圖分類號(hào)：TP273

文獻(xiàn)標(biāo)志碼：A

DOI:10.16086/j.cnki.issn1000-0380.201507024

山東省自然科學(xué)基金資助項(xiàng)目(編號(hào)：ZR2011FQ022、ZR2012FQ018)；

中國(guó)科學(xué)院自動(dòng)化研究所開放課題資助項(xiàng)目(編號(hào)：20140109)。

修改稿收到日期：2015-01-16。

第一作者李敏花(1981-)，女，2009年畢業(yè)于中國(guó)科學(xué)院自動(dòng)化研究所模式識(shí)別與智能系統(tǒng)專業(yè)，獲博士學(xué)位，副教授；主要從事機(jī)器人控制、圖像處理、機(jī)器視覺等方面的研究。