基于顯式算法的船體梁極限強度非線性有限元分析

李政杰，趙 南，司海龍，虞 昊

(中國船舶科學研究中心，江蘇無錫214082)

0 引言

隨著現代船舶的大型化發展，船體結構強度問題不斷凸顯，有關船體結構真實強度的極限強度和破損后的極限承載能力，近幾年來已受到越來越多的關注。多家船級社［1－3］的設計標準中已經規定了關于船體結構總縱極限強度的要求，未來向其他船型普及和貫徹極限強度要求的趨勢亦愈來愈明顯。

船體梁極限強度作為評價結構極限承載能力的重要指標，目前，其研究手段主要有直接計算法、逐步破壞法、理想結構單元法、實船事故調查和模型試驗、非線性有限元法6種。表1分別對各種計算方法進行了對比，通過對比可以看出非線性有限元法是計算和分析船體極限強度的一種強有力工具，能夠合理地處理結構的邊界條件、載荷形式、模型細節、單元類型等影響因素，可以綜合考慮結構的初始缺陷和材料的非線性特性，比較直觀地模擬結構屈曲崩潰的過程并清晰地反映其后屈曲特性。

船體梁極限強度非線性有限元計算中，隱式算法較為常見，但其計算過程需要多次迭代，存在收斂問題，增量步長較大，總的增量步數較少。隱式算法對增量步的大小沒有限制，增量步大小主要取決于求解精度和收斂條件，每個增量步上需要進行多次迭代，求解復雜非線性問題的計算代價較大。因此，有必要采用顯式算法，改變求解策略，提高計算效率。

1 顯示算法

顯式算法和隱式算法都是求解非線性問題強有力的工具。所謂顯式算法和隱式算法，是指求解策略的不同，即數學上的出發點不一樣。顯式算法中一般適用于求解應力波效果顯著或模擬時間非常短暫 (一般小于1 s)的分析，如高度不連續的高速的動力學分析、復雜的接觸分析、復雜的后屈曲分析、高度非線性分析的準靜態分析、邊界條件極度不連續的問題、材料磨損和材料失效等，其計算過程不需要迭代，不存在收斂問題，增量步很小，總的增量步很多，增量步的大小與模型的最大固有頻率有關，與載荷類型和載荷持續時間無關。

顯式算法一般采用中心差分法顯示地對運動方程在時間域上進行積分，利用上一步增量步的平衡方程動態地計算下一步增量步的狀態。顯示求解器的中心差分算子在每一增量步的開始時刻t滿足動態平衡方程，通過計算t時刻的加速度，將速度的計算結果推進到t+，將位移的計算結果推到t+Δt。每一增量步結束時刻的狀態完全由增量步開始時刻的位移、速度和加速度決定。

隱式算法是將一個分析步分解為多個增量步，載荷則以增量的形式逐步施加，在每個載荷增量步中都要進行一系列迭代，在每次迭代中使用上一次的迭代得到的修正剛度矩陣進行計算。這樣，對計算結果逐步修正，直到滿足平衡方程，達到收斂。在每一增量步內都需要對平衡方程組 (隱式表達式)進行迭代求解，每次都需要對非線性剛度矩陣求逆，計算成本相對較大，但是隱式算法的計算比較穩定，大多數時候是無條件的穩定，對步長的要求不高。

在計算復雜的船體梁極限強度時發現由于結構復雜，單元數量過多，或者材料的非線性、結構幾何非線性、邊界非線性等的影響運用隱式算法常常不收斂，得不到可靠地數值解。因此，可考慮使用動態分析近似模擬靜力加載過程，即準靜態分析，采用顯式算法進行求解。

假設結構的非線性靜態平衡方程為:

式中:P為載荷列陣;I為內力列陣。

顯示有限元法運用中心差分法對在時間上對運動方程進行積分，應用一個增量步的動力學條件計算下一個增量步的動力學條件。在增量步開始時，程序求解動力學平衡方程，表示為節點質量矩陣M和加速度u·的乘積等于節點的內力，即施加的外力P與內力I的差值:

在當前增量步開始時，假設是t時刻，計算加速度為:

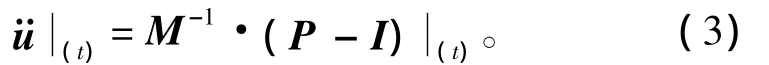
因為顯式算法總是采用對角的或者集中的質量矩陣，所以求解加速度并不復雜，不需要同時求解兩聯立方程。任何節點的加速度完全取決于節點質量和作用在節點的合力，使得節點計算成本非常低。

采用中心差分法對加速度在時間上進行積分，在計算速度的變化時假設加速度為常數。應用這個速度的變化值加上前一個增量步中點的速度確定當前增量步中點的速度:

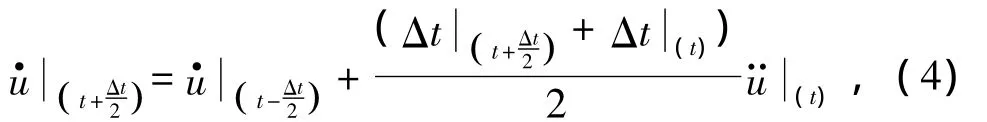
速度對時間的積分加上增量步開始時的位移來確定在增量步結束時的位移:

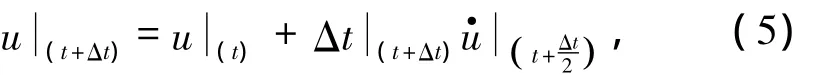
這樣，在增量開始時提供了滿足動力學平衡條件的加速度。得到了加速度，在時間上“顯式地”前推速度和位移。所謂“顯式”是指在增量步結束時的狀態僅依靠于該增量步開始前的位移、速度和加速度。為了得到精確的結果，需要假定在載荷隨時間增長非常慢，這樣在增量步中的加速度幾乎為零，這就是所謂的準靜態。下面給出顯示動力方法的總結:

1)節點計算

①動力平衡方程

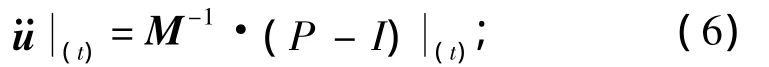
②對時間進行顯示積分

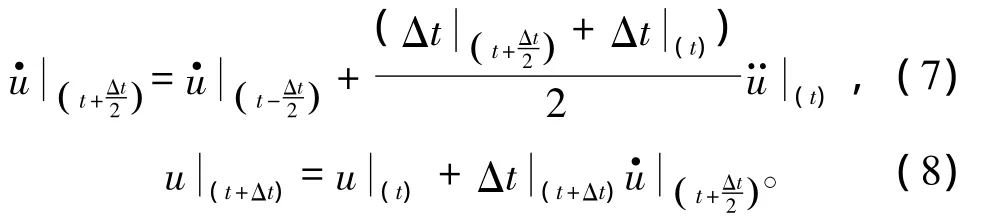
2)單元計算

②根據本構關系計算應力σ

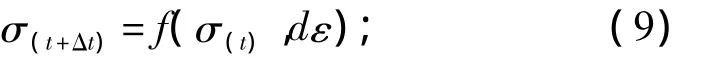
③ 集成節點內力I(t+Δt)，

3)設置時間t為t+Δt，返回到步驟1)。

2 顯示算法與隱式算法算例對比

利用大型通用軟件Abaqus，分別采用顯式算法和隱式算法對Nishihara箱型梁模型進行對比計算，并將計算結果與試驗值［4］比較，驗證和比較隱式算法和顯示準靜態算法在計算船體梁極限強度中的實用性和可靠性。

Nishihara箱型梁的結構尺寸如表2，采用理想彈塑性材料，模型兩端采用多點約束，兩主節點簡支，施加垂向角位移。假設焊接殘余拉壓應力影響相互抵消，忽略殘余應力影響;初始變形采用一階屈曲模態來模擬，幅值為1.48 mm。箱型梁的有限元模型如圖1所示。

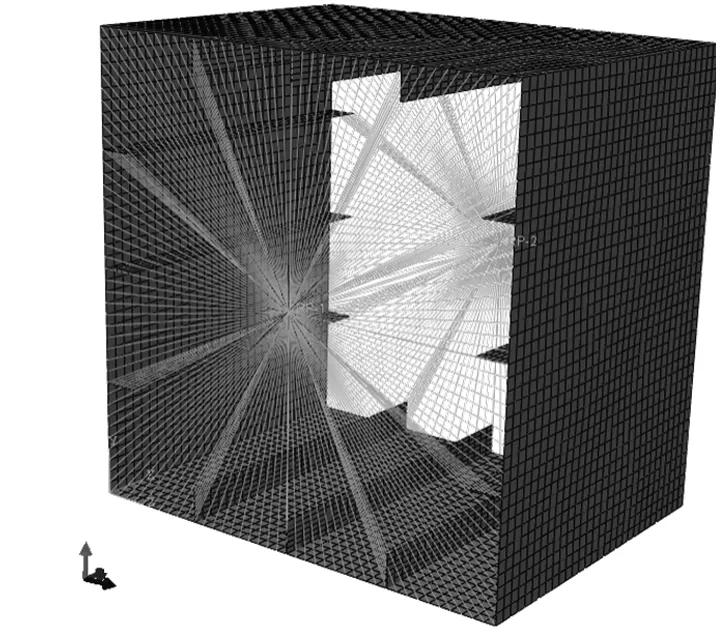
圖1 Nishihara箱型梁有限元模型Fig.1 The FEM model of Nishihara box girder

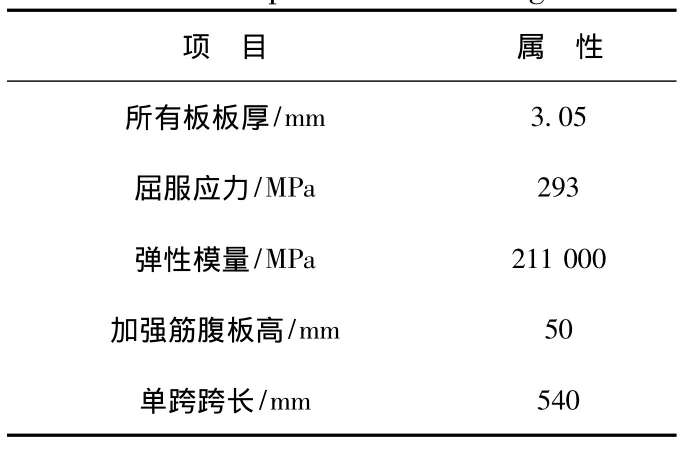
表2 箱型梁模型參數Tab.2 The parameter of box girder

圖2和圖3分別給出了隱式算法和顯式算法極限狀態下箱型梁應力云圖，對比兩圖可看出，2種應力分布云圖基本一致。

圖2 極限狀態應力分布云圖 (隱式算法)Fig.2 The stress tensor of ultimate state(implicit algorithm)

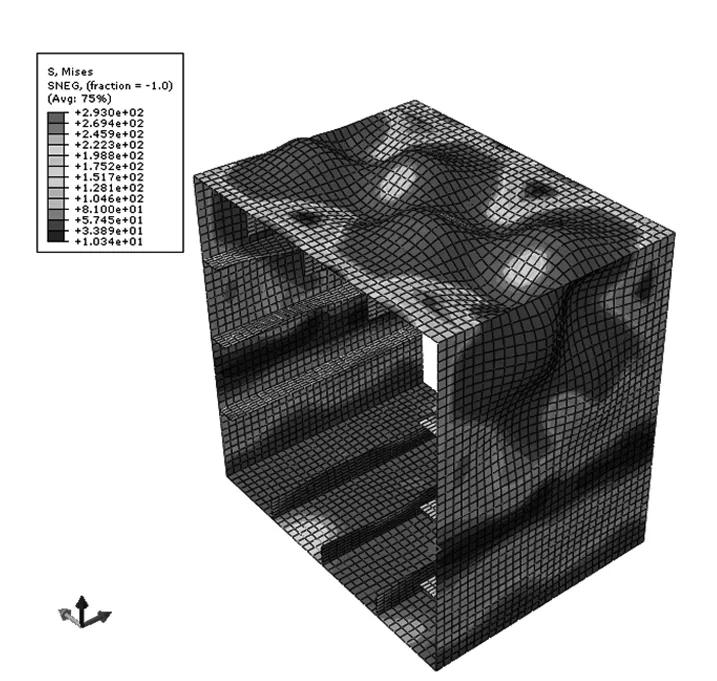
圖3 極限狀態應力分布云圖 (顯式算法)Fig.3 The stress tensor of ultimate state(explicit algorithm)

圖4給出了2種算法的載荷－位移曲線，2條彎矩－轉角曲線基本一致，在達到峰值點之前，結構處于線性狀態，兩曲線重合;達到峰值后，進入塑性的部件逐漸增加，顯式算法存在著能量損耗，與靜態分析存在細微差別，由此表現出來結構的后屈曲性能存在稍微差別。總體而言，兩者計算的結果比較一致。

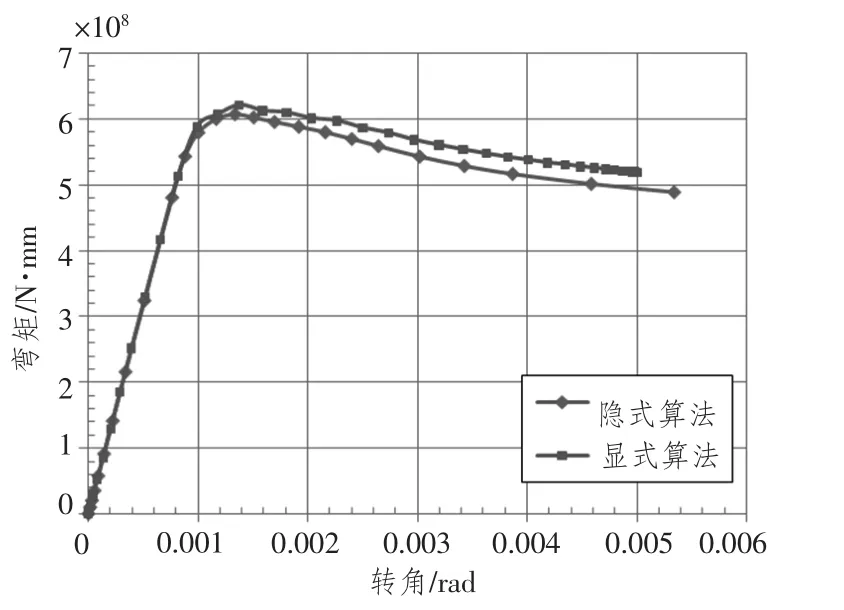
圖4 不同算法彎矩－轉角曲線Fig.4 Bending moment-angle curve of different algorithms

表3給出了2種算法的計算結果及試驗值。隱式算法與試驗結果比較的相對誤差為3.06%，顯式算法與試驗結果比較的相對誤差為5.44%;顯式算法相對隱式算法計算結果稍大，這是由于顯式算法屬于準靜態求解，其求解步長稍大，以致結果存在稍許誤差;而顯式算法求解的時間約為隱式求解時間的一半，其計算效率較高。當結構較為復雜時，隱式算法的計算時間將大大增加。

表3 箱型梁計算結果對比 (108 N·mm)Tab.3 The calculate result of box girder comparison(108N·mm)

對比分析2種計算的結果:隱式算法的計算精度較高，但其計算效率較低;顯式算法計算精度相對隱式算法稍低，但也滿足工程設計需要，其計算效率較高。當結構較為復雜時，隱式算法的收斂性較差，往往不能得到收斂的結果，造成計算失敗;顯式算法其收斂性較好，選擇適當的計算步長，能夠得到滿足要求的收斂解。綜合考慮計算的精度和效率，基于顯式算法的船體梁極限強度計算具有較高的優勢。

3 目標實船計算

Dow's 1/3 test hull模型［5］具有較高的代表性，許多學者對其進行了對比計算，其結果常被用來檢驗計算方法的精度和適用性。Dow試驗模型尺寸如圖5所示。

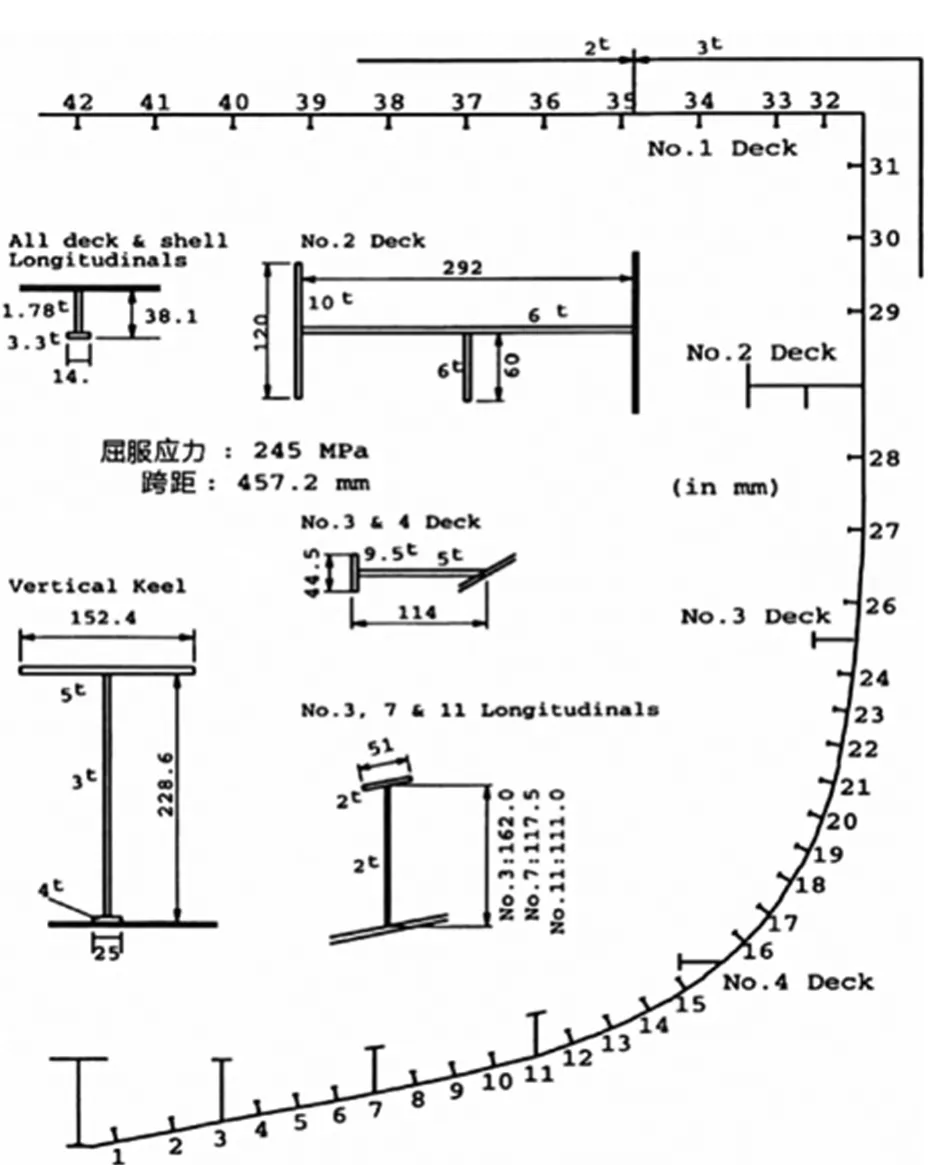
圖5 Dow's test hull剖面Fig.5 The section of Dow's test hull

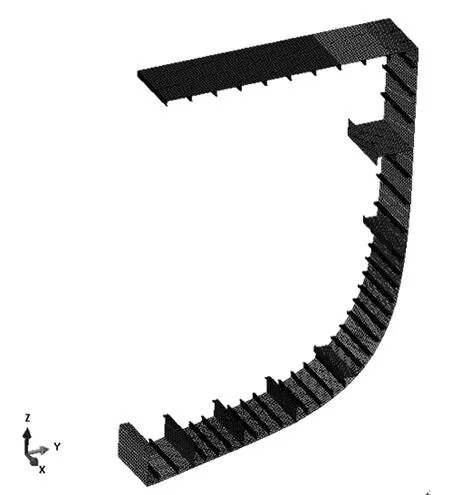
圖6 有限元模型Fig.6 The FEM model

運用顯式算法，采用單跨模型計算其極限承載能力。模型初始變形形狀采用其一階模態，其變形幅值為試驗測得變形量;忽略殘余應力的影響，其有限元模型如圖6所示。采用理想彈塑性材料，模型兩端采用多點約束，兩主節點簡支，施加垂向轉角位移。

圖7和圖8分別給出了Dow模型中拱和中垂2種極限狀態下的應力分布云圖，圖9給出了模型的端面彎矩－轉角曲線。

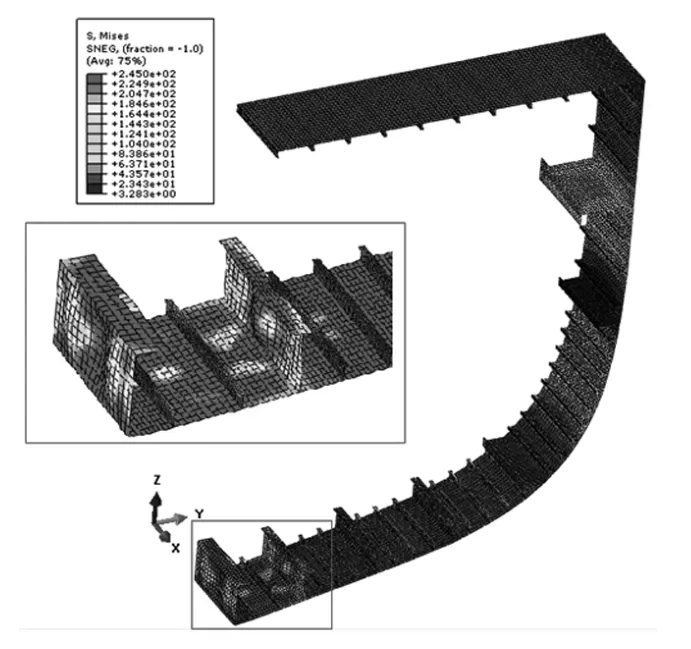
圖7 中拱極限狀態下應力分布云圖Fig.7 The stress tensor of hog ultimate state

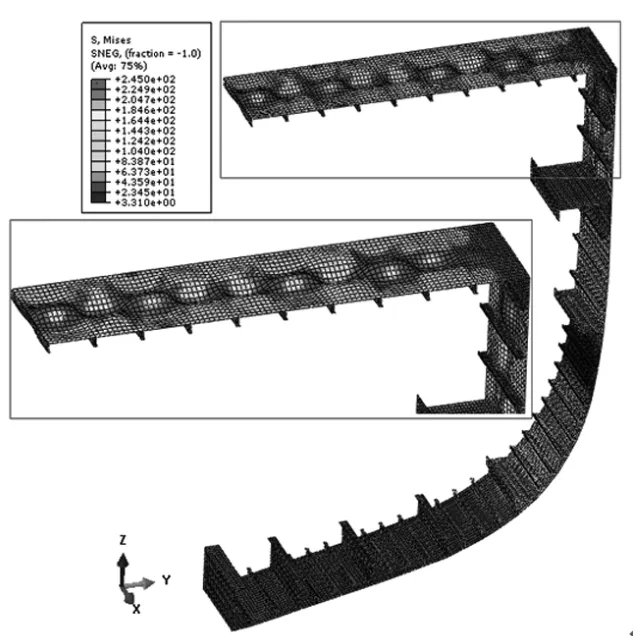
圖8 中垂極限狀態下應力分布云圖Fig.8 The stress tensor of sag ultimate state

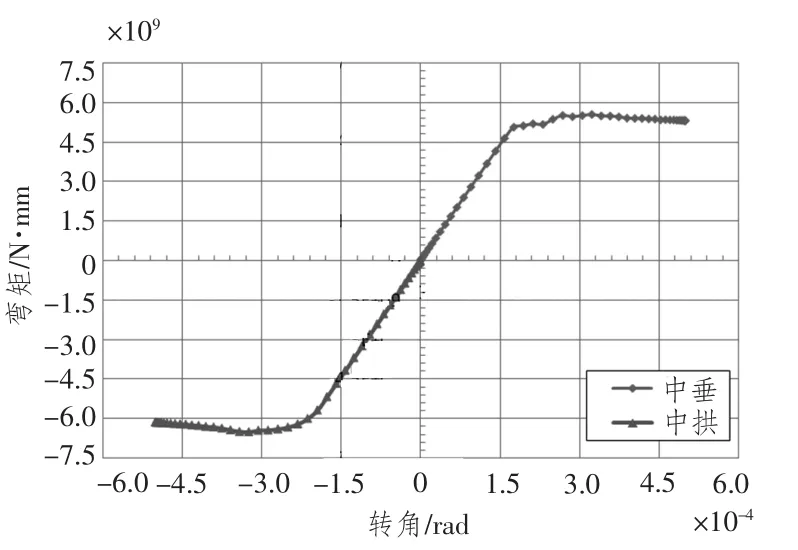
圖9 Dow模型 (1/2)彎矩－轉角曲線Fig.9 Bending moment-angle curve of Dow model(1/2)

表4給出了2種極限狀態下模型的極限強度值，并與其他學者的計算結果進行比較。顯示計算的結果稍微偏大，這是因為采用1/2對稱模型，約束強化結構，并且未考慮殘余應力的影響。

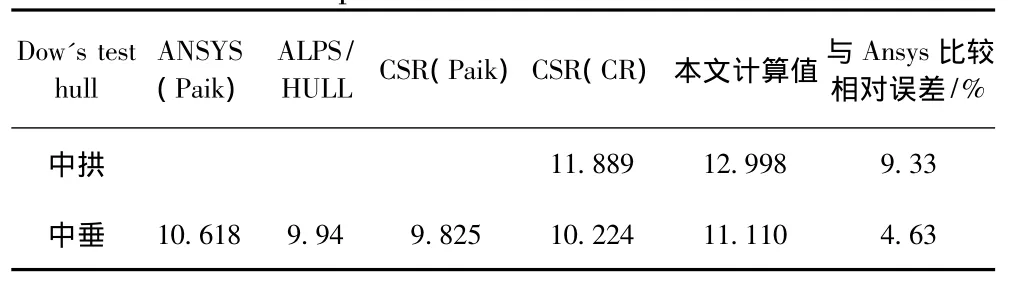
表4 Dow's test hull計算結果比較Tab.4 The comparison for the result of Dow's test hull

4 結語

本文對有限元計算中的顯示算法進行了介紹，并采用顯式算法和隱式算法對Nishihara模型的極限強度的計算結果進行對比分析，發現顯式算法具有較好的精度且計算效率較高;基于顯式算法對Dow船體梁模型的極限強度進行計算，并與相關研究結果比較，結果表明該方法具有良好的計算精度，可以用于實船的極限強度分析，為船體結構的設計提供參考。

［1］ IACS．Common Structural Rules for Bulk Carriers［S］．2008．

［2］ ABS Rules for Building and Classing Steel Vessel Rules［S］．Houston，2013．

［3］ DNV Rules for Classification of Ships［S］．Norway，2013．

［4］ Nishihara S．Ultimate longitudinal strength of midship cross section［J］．Naval Arch．Ocean Eng，1984，22:200 －214．

［5］ ISSC report of special task committee VI．2，ultimate hull girder strength．In:Ohtsubo H， Sumi Y， editors．Proceedings of the 14th international ship and offshore structures congress，Nagasaki，Japan;October 2000．