復合材料螺旋槳雙向流固耦合計算

楊 光，熊 鷹，黃 政

(海軍工程大學艦船工程系，湖北武漢430033)

0 引言

復合材料從問世以來就備受關注，最初被應用于航空航天領域，當今在船舶領域也得到了重視，并逐漸開始將復合材料應用于螺旋槳上。因其較輕的比重、超強的耐腐蝕性、良好的非磁性能、獨特的彎扭耦合特性和優異的阻尼性能，使得復合材料螺旋槳較傳統金屬材料螺旋槳在性能方面體現出諸多優勢［1］。傳統的金屬螺旋槳在進行水動力計算時，并不考慮變形，視為剛性體，但復合材料螺旋槳在水中運轉時，會產生較大變形，這與金屬材料螺旋槳有很大不同，因此對復合材料螺旋槳進行設計和性能預報時，要考慮流場作用下槳葉的變形和槳葉的變形對周圍流場的相互影響。Lin等［2－3］采用渦格法 (VLM)結合有限元方法對復合材料螺旋槳進行水彈性分析，但并未考慮流體與結構相互作用的影響;Young［4］采用邊界元法結合有限元法對復合材料螺旋槳進行流固耦合計算;海軍工程大學孫海濤［5－6］采用低階面元法結合有限元法建立了考慮流體結構相互作用的迭代求解算法;張帥［7］采用弱耦合的方法對某系列螺旋槳進行流固耦合運算。

在以往的研究中，采用流固耦合方法對水動力性能進行計算時大多基于勢流理論，沒有考慮流體的粘性作用，而且流固耦合大多是單向的，并不考慮流體和結構的相互作用。本文以DTMB4381槳為研究對象，考慮流體與結構的相互作用，采用基于粘性流理論的計算流體力學方法結合有限元軟件對不考慮鋪層結構的玻璃纖維復合材料螺旋槳和鎳鋁青銅螺旋槳分別進行雙向流固耦合計算，研究材料對螺旋槳水動力性能和結構特性的影響。

1 數值計算方法

1.1 流體力學控制方程

質量守恒定律和動量守恒定律是流體流動現象的基本守恒定律。由于計算機內存和速度的限制，直接求解三維非穩態N－S方程是不能被普遍推廣的，因此采用Reynolds平均法對N－S方程進行時均化處理。時均形式的N－S方程多出了Reynolds應力項，需要引入湍流模型使方程組封閉。

質量守恒方程:

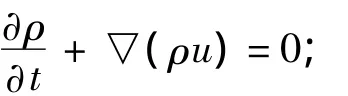
Reynolds方程:

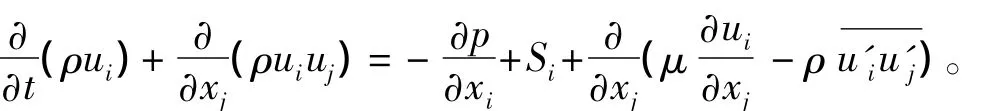
式中:ρ為液體密度;u為速度矢量;p為液體壓力;Si為源項。

1.2 流固耦合控制方程

在固定坐標系下，螺旋槳以恒定轉速繞著旋轉軸運轉的運動方程如下:

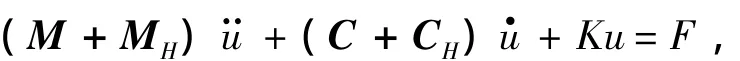
阻尼在結構振動中是一個重要參數，但在實際中要完全反映結構的阻尼特性很困難，在本文中將結構阻尼特性簡化，采用Rayleigh阻尼

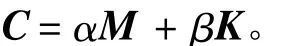
式中:α為質量比阻尼系數;β為剛度比阻尼系數系數，可通過試驗確定。

2 計算模型

本文以DTMB4381槳為研究對象，DTMB4381為5葉槳，槳葉直徑為0.305 m，設計進速系數為J=0.889。螺旋槳的材料分別為鎳鋁青銅合金和玻璃纖維，本文中玻璃纖維不考慮鋪層結構，視為各向同性。

2.1 流體計算模型

本文采用ICEM CFD建立流體計算域模型，為了提高計算效率，流體計算采用1/5單通道模型，如圖1所示。X軸負方向為來流方向，采用動滑移網格技術將計算域分為靜止域與旋轉域兩部分，旋轉域模型如圖2所示，2個流域的交界面應用GGI技術連接，本文網格劃分采用六面體網格，為了能夠更好地捕捉槳葉周邊流場的流動情況，在槳葉周圍需要加密網格，確保值在300以內，本文取小于150來確定邊界層尺度。最終，網格數約為1 400 000。網格質量保持在0.2以上。

圖1 單通道流體計算域Fig.1 Computation domain of fluid

圖2 旋轉域Fig.2 Rotating domain

為了確保流固耦合計算能夠成功，先不考慮流固耦合作用，采用CFX流體計算軟件對此單通道模型進行水動力計算。采用SST湍流模型，殘差設為10－7，轉速設為600 r/min，通過改變來流速度，得到進速系數在J=0.4～1.0工況下的水動力性能，并與鎳鋁青銅螺旋槳的敞水試驗值進行對比，得到推力系數、轉矩系數10、效率η的最大誤差分別為5.3%、5.6%、1.9%，誤差在工程應用允許范圍內，驗證了此單通道模型可以用來對復合材料螺旋槳進行雙向流固耦合計算。

2.2 結構計算模型

通過Matlab編程，根據DTMB4381槳型值得到槳葉各半徑處的三維坐標點，然后導入到SolidWorks建模軟件中建立螺旋槳實體模型。本文采用單通道計算模型，因此結構計算只需取單個實體槳葉模型，采用Ansys Mechanical自帶網格劃分模塊對槳葉模型進行實體網格劃分，并在葉梢及葉根等處進行局部加密，最終實體網格數為6 474，如圖3所示。在葉根處設置固定約束，設置槳葉旋轉速度為600 r/min。為了實現流體計算結果與固體結構計算結果在流固耦合面上相互交換傳遞，分別設置槳葉壓力面和吸力面為流固耦合面。分別設置螺旋槳材料為鎳鋁青銅合金和玻璃纖維。為了體現復合材料螺旋槳的阻尼特性，在設置玻璃纖維材料時，增加了對Rayleigh阻尼系數的設置，設置α=3，β=0。2種材料參數如表1所示。

表1 材料參數Tab.1 Material property

圖3 槳葉有限元模型Fig.3 Finite element mesh of blade

2.3 流固耦合求解

在Workbench平臺上，通過Transient Structural模塊以及CFX流體計算模塊之間的數據傳遞實現流固耦合計算。結構模塊和流體計算模塊中設置螺旋槳轉速為n=600 r/min，通過改變來流速度得到進速系 數 J = 0.4，0.5，0.6，0.7，0.8，0.889，0.9，1.0的不同工況。湍流模型選擇SST，設置來流入口的邊界條件為速度入口，出口設置為壓力出口邊界條件，相對壓力設置為0，流域的左右兩邊界設置為周期性邊界條件，遠場設置為開放式邊界條件。時間步長取為0.05 s，流體計算以及結構計算的殘差均取為0.000 1。水動力性能計算結果和結構性能計算結果通過多場求解器MFX進行耦合迭代，直到滿足殘差要求計算停止。

3 計算結果分析

3.1 水動力結果分析

通過雙向流固耦合計算得到鎳鋁青銅合金和玻璃纖維螺旋槳在不同進速系數下的水動力性能，如表2所示。比較雙向流固耦合計算得到的鎳鋁青銅合金螺旋槳水動力性能與敞水試驗值，如圖4所示，得到推力系數、轉矩系數、效率與敞水試驗值的最大誤差分別為5.4%，5.8%，1.9%，誤差滿足工程應用的要求。結果基本與不考慮耦合的水動力性能基本一樣，驗證了工程中將金屬槳視為剛性槳假設的合理性。誤差產生原因有以下幾點:本文采用單通道計算模型，并沒有考慮槳轂對流場的影響;而且單通道模型也沒有考慮槳葉之間的相互干擾。

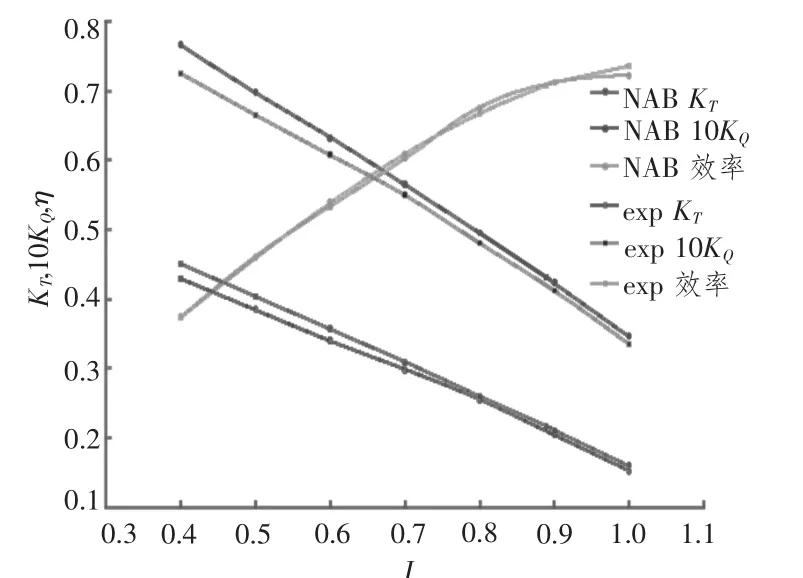
圖4 4381耦合水動力性能與試驗值對比Fig.4 Comparison of 4381 FSI hydrodynamic performance with experimental results

通過比較鎳鋁青銅合金和玻璃纖維螺旋槳水動力性能的雙向流固耦合結果可知，2種材料螺旋槳的水動力性能比較接近。但從下文可知，各向同性的玻璃纖維螺旋槳的變形量比鎳鋁青銅螺旋槳高一個數量級，導致這種結果的原因可能是玻璃纖維螺旋槳并沒有考慮鋪層結構，復合材料為各向同性，導邊到隨邊的變形較為均勻。玻璃纖維螺旋槳的推力系數、轉矩系數在J=0.4～1.0工況下均大于鎳鋁青銅合金螺旋槳，并且隨著進速系數的增加，差值逐漸減小;玻璃纖維螺旋槳的效率在進速系數J=0.4～0.9工況下均低于鎳鋁青銅合金螺旋槳;在J=1.0工況下，玻璃纖維螺旋槳效率較鎳鋁青銅合金螺旋槳略有增加。推力系數、轉矩系數、效率在進速系數J=0.4時相差最大，相對差值分別為0.78%，1.04%，0.26%。雖然各向同性的玻璃纖維材料對螺旋槳水動力性能影響不大，但由結果可知通過選擇合理的鋪層方式以及材料體系能夠改善螺旋槳的水動力性能。

表2 螺旋槳水動力性能Tab.2 Hydrodynamic performance of propeller

3.2 結構計算結果分析

計算收斂后得到了2種材料螺旋槳在不同進速系數下的變形情況。由圖5可得，在相同轉速下，2種材料螺旋槳的最大變形量隨著進速系數的增加而減小，并且玻璃纖維螺旋槳的最大變形量較鎳鋁青銅合金螺旋槳高一個數量級。圖6與圖7分別為2種材料螺旋槳不同進速系數下的最大變形，為了使變形更加明顯，經過適當的放大處理。由變形云圖可知2種材料螺旋槳的最大變形均出現在葉梢部位，變形量由葉根至葉梢沿徑向逐漸增加，而且2種材料螺旋槳在同一半徑處沿著槳軸方向導邊變形量要大于隨邊，使槳葉向隨邊傾斜，引起了側斜角的增加，改變了各半徑處螺距分布。槳葉由于受到水的推力，向船首方向傾斜，使槳葉產生了縱傾。若不考慮誘導速度，某半徑處槳葉剖面的速度多邊形如圖8所示，根據玻璃纖維螺旋槳變形情況可得，在相同轉速、相同進速下，水動力螺距角β保持不變，槳葉螺距角θ變大，導致攻角K變大，因此，在相同進速系數下，玻璃纖維螺旋槳的推力及扭矩比鎳鋁青銅合金螺旋槳有所增加，導致水動力性能的變化。

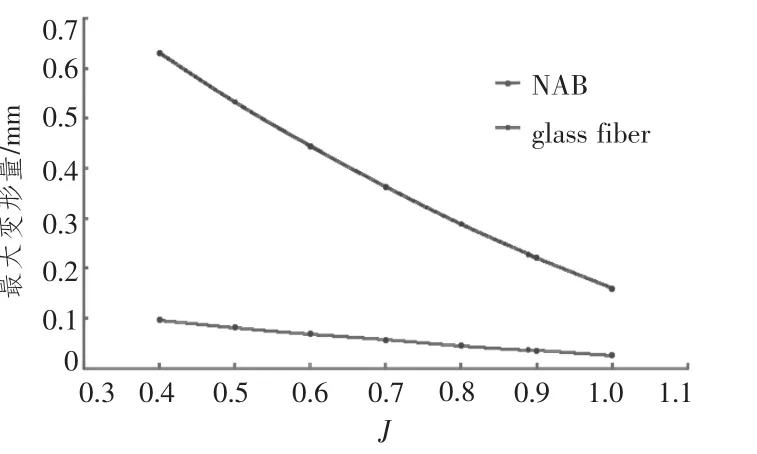
圖5 不同進速系數下螺旋槳最大變形Fig.5 Maximum deformation at different J

圖6 玻璃纖維螺旋槳變形Fig.6 Total deformation distribution of glass fiber blade

圖7 鎳鋁青銅合金螺旋槳變形Fig.7 Total deformation distribution of NAB blade

圖8 葉元體的速度多邊形Fig.8 Flow around a blade section

圖9為2種材料不同進速下最大等效應力的對比。由圖可知，玻璃纖維螺旋槳在進速系數J=0.4～1.0工況下的等效應力均大于鎳鋁青銅合金螺旋槳，隨著進速系數的增加，2種材料螺旋槳的最大等效應力逐漸減小。雖然玻璃纖維螺旋槳的變形量較鎳鋁青銅合金螺旋槳高一個數量級，但其彈性模量較鎳鋁青銅合金小，導致玻璃纖維螺旋槳的等效應力略大于鎳鋁青銅合金螺旋槳。根據圖10和圖11可得，2種材料DTMB4381螺旋槳所受最大應力均出現在葉根中心位置處，而且應力沿著徑向逐漸減小。因此在對復合材料螺旋槳進行鋪層設計時，要著重增強葉根處的承載強度。

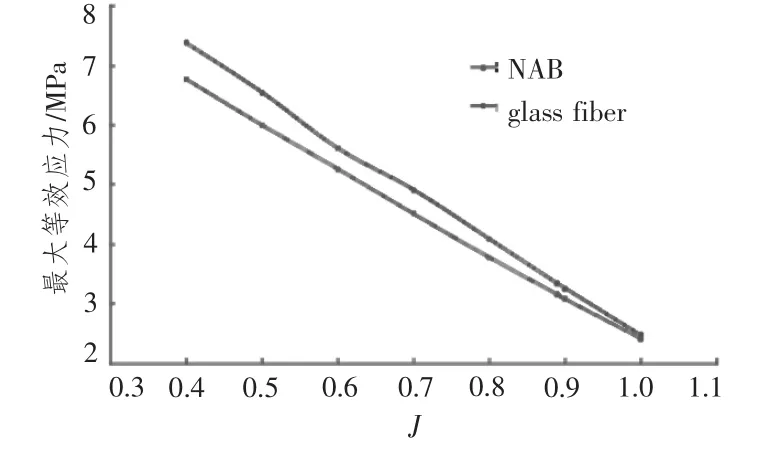
圖9 不同進速系數下螺旋槳最大應力Fig.9 Maximum stress at different J

圖10 玻璃纖維螺旋槳應力分布Fig.10 Stress distribution of glass fiber blade

圖11 鎳鋁青銅合金螺旋槳應力分布Fig.11 Stress distribution of NAB blade

4 結語

本文采用計算流體力學方法結合有限元結構計算軟件，選用DTMB4381槳為研究對象，賦予玻璃纖維和鎳鋁青銅合金2種不同的材料屬性，分別在不同進速系數工況下進行雙向流固耦合計算，計算得到了不同材料螺旋槳的水動力性能和結構特性，通過比較分析得出如下結論:

1)考慮鎳鋁青銅合金螺旋槳的微小變形，對其進行雙向流固耦合計算，得到了推力系數、轉矩系數、效率等水動力參數，并與敞水試驗值進行對比，誤差較小，驗證了本文雙向流固耦合方法的可行性。

2)通過計算得到了不同材料螺旋槳結構特性的一般規律，纖維材料螺旋槳所受等效應力要大于傳統的金屬材料螺旋槳，并且等效應力由葉根至葉梢沿徑向逐漸減小，因此在設計復合材料螺旋槳時要注意葉根部位承載強度的加強。復合材料螺旋槳具有獨特的彎扭耦合特性，運轉時螺旋槳的縱傾、側斜以及螺距分布均有改變，若能有效利用復合材料螺旋槳的彎扭耦合特性，對提高螺旋槳效率、減少空泡等有十分重要的作用。

3)通過比較不同材料螺旋槳的流固耦合特性可得，纖維復合材料影響螺旋槳水動力性能和結構特性，通過優選鋪層方式以及材料能夠有效地提高螺旋槳效率。因此復合材料螺旋槳必須考慮流體與結構的耦合作用。

［1］ 駱海民，洪毅，魏康軍，等．復合材料螺旋槳的應用、研究及發展［J］．纖維復合材料，2012，1(3):3 －6．LUO Hai-min，HONG Yi，WEI Kang-jun，et al．The application and study and development of composite propeller［J］．Fiber Composites，2012，1(3):3 －6．

［2］ LIN G．Comparative stress-deflection analyses of a thickshell composite propeller blade［R］．David Taylor Research Center，DTRC/SHD －1373 －01，1991a．

［3］ LIN G．Three-dimensional stress analyses of a fiberreinforced composite thruster blade［C］//symposium on Propellers/shafting Society of Naval Architects and Marine Engineers．Virginia Beach，VA，USA，1991b．

［4］ YOUNG Y L．Fluid-structure interaction analysis of flexible composite marine propellers［J］．Journal of Fluids and Structures，2008，24(6):799 －818．

［5］ 孫海濤，熊鷹．考慮變形的螺旋槳水動力及變形特性研究［J］．哈爾濱工程大學學報，2013，34(9):1108 －1118．SUN Hai-tao，XIONG Ying．Study on hydrodynamic and deformation performance of propellers considering the blade deformation［J］．Journal of Harbin Engineering University，2013，34(9):1108 －1118．

［6］ 孫海濤，熊鷹．槳葉變形對復合材料螺旋槳水動力性能影響［J］．華中科技大學學報，2013，41(6):81 －85．SUN Hai-tao，XIONG Ying．Effect of blade deformation of a composite propeller on its hydrodynamic performance［J］．Journal of Huazhong University of Science and Technology，2013，41(6):81 －85．

［7］ 張帥，朱錫，周振龍，等．易變形船舶螺旋槳流固耦合特性分析［J］．海軍工程大學學報，2014，26(1):48 －53．ZHANG Shuai，ZHU Xi，ZHOU Zhen-long，et al．Fluidstructure interaction characteristics for flexible marine propellers［J］．Journal of Naval University of Engineering，2014，26(1):48 －53．