雙股線幾何強力模型的建立及其影響因素

黃 偉，汪 軍，2

(1.東華大學紡織學院，上海 201620;2.東華大學紡織面料技術教育部重點實驗室，上海 201620)

紗線結構的研究開始于20世紀30年代，落后于纖維和織物，到50年代才有了較為明顯的進展［1］。在分析紗線結構時，由于其復雜性和多重性，所以往往需要從纖維排列的理想狀態(tài)入手，建立紗線理想的幾何模型［2］。其中一些研究者從理論角度上的研究既系統(tǒng)又詳盡。理論成果包括Platt［3－4］提出了紗線張力應變與纖維張力應變的關系;Hearle［5］考慮拉伸力、橫向力與外側收縮的作用影響，推導了張壓應力在紗線不同位置上的關系表達;后來Nachane［6］從單紗段的短片段受力分析入手認為，單紗中的張力分量和剪切分量共同貢獻了紗線的伸長，推導了能較好符合實驗趨勢的雙股線張力拉伸方程;此后他通過進一步研究推導出理想加捻復合長絲紗關于載荷、伸長和比模量的公式［7］，比前人的研究在公式預測上與實驗數據更加接近。本文研究運用該方法建立了關于雙股線結構的理想幾何模型，并在此基礎上研究股線捻度和單紗之間的作用力與其強力的關系。

1 股線強力增強效應

本文研究的對象股線作為其在結構上的體現，是由2根及以上的單紗(長絲或短纖紗)并合加捻而成，其中雙股線是最簡單的股線種類，如圖1所示(θ為捻回角，rf為單紗半徑)。經多項實驗和生產數據所得，加捻是股線增強效應的主要因素［8］，這種股線強力超過組成單紗強力之和的現象稱為股線增強效應。對于這種現象的本質研究，國內外也有許多研究成果予以論證。通過實驗數據與理論上對股線強力的增強效應影響因素分析得到，加捻能使纖維間的抱合和交互作用增強，從而使斷裂不同時性降低，在低捻和長絲紗中尤為明顯。纖維間作用力的增強直接體現為纖維間摩擦力的增加，從而增強整體紗線的強力，但當捻度增加到一定程度后，過大的單紗傾斜角使纖維軸向分力減小，影響其強力的有效利用，因此在捻度和橫向壓力的雙重影響下，紗線的強力在隨捻度增加的過程中存在極大值，此時紗線的捻系數被稱為臨界捻系數，而這種現象在股線加捻的過程中同樣存在。

圖1 雙股線幾何模型Fig.1 Geometric model of ply yarn.(a)Longitudinal section;(b)Cross section

但是關于股線強力的研究目前大都停留在借助實驗來探尋數據變量之間的規(guī)律，缺乏定量分析。從常見的紗線參數入手，建立了關于雙股線的幾何模型，分析了單紗短片段在拉伸載荷下的拉伸行為;然后將股線捻度與單紗之間的摩擦力作為影響股線強力的主要因素，最終以較少的變量參數推導了股線的強力表達式，并證明了股線具有類似于單紗加捻時臨界捻系數的存在。

2 模型建立及求解

考慮到長絲股線的強力組成主要由其單紗性能及單紗之間因加捻彎曲而產生的抱合力決定，故分別研究單紗性能對股線拉伸行為的影響與拉伸時抱合力引起的單紗之間摩擦力對強力貢獻的情況，方法上遵循經典力學上物理變量的關系。

2.1 條件假設

雙股長絲紗拉伸強力對股線與單紗捻比變化不顯著，故可忽略單紗捻度的存在;且股線的拉伸行為類似于單紗［9］。建立理想模型如圖1所示，并作如下假設:1)單紗為1根連續(xù)長絲紗，截面圓形，沿長度方向均勻，且2根單紗性質相同;2)單紗路徑為等螺旋線，離股線軸線距離不變，傾斜角不變，即捻度沿軸線方向不變;3)考慮為低捻環(huán)境下，忽略因加捻程度不同而引起的單紗預伸長的影響，捻回角與單紗線密度隨加捻過程及拉伸過程中的變化;4)在單紗拉伸伸長過程中，紗線應力與應變的關系遵循胡克定律，即拉伸模量為定值;5)因加捻而使單紗之間產生的抱合力在單紗長度方向上處處相等。

2.2 模型構成

對股線的拉伸強力和增強效應影響因素分析之后可得，股線總強力由2部分組成:一是假設為遵循胡克定律而線性增加的拉伸力;二是在拉伸時因加捻產生的單紗間相互作用力，在此體現為單紗之間摩擦阻力，體現在公式關系即為:

式中:Tt為股線總強力;Ty為股線拉伸力;fy為摩擦阻力。以下分別推導等式右邊的變量表達式。

2.3 模型求解

1)根據連續(xù)介質力學理論結合假設條件，拉伸力的基本公式為:

式中:Ay為紗線橫截面面積;εy為斷裂應變;Ey為股線拉伸模量。

據圖1所示，rf為單紗半徑，則雙股線截面情況為

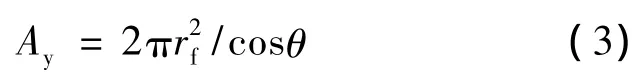
Ey是由單紗模量和捻回角確定的，如圖2所示。假設紗線承受載荷2T的作用，每根長絲沿紗軸方向承受T的載荷，分解而得的拉伸分力Tcosθ和剪切分力Tsinθ共同導致了紗線的伸長。則在一個螺線捻度內的單紗長度Lf貢獻給沿紗軸上的伸長為

又因為在一個捻度內單紗長度Lf與股線長度Ly存在Ly=Lfcosθ的關系，則股線應變△Ly/Lf為

則據式(2)，Ty=2T，拉伸模量為

式中:Y為單紗彈性模量;K為單紗剪切模量;θ為股線捻回角。

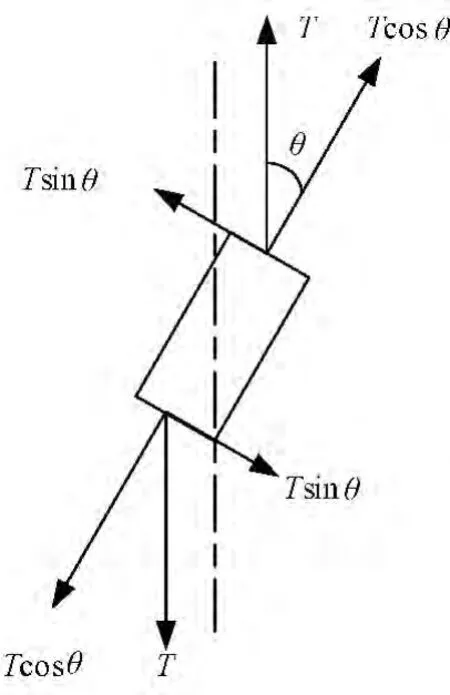
圖2 短片段上力的分解Fig.2 Directions of forces acting on an element in Nachane's study

2)復合紗線中2組成分之間摩擦阻力的計算方法［10］如下:

式中:μ為摩擦因數;N為徑向壓力;α為抱合系數;S為接觸面積。

徑向壓力即單紗因加捻彎曲產生的向心壓力，關系如圖3所示［11］，則可得到以下關系式:

又因為當 φ 很小時，sinφ/2 ≈ φ/2;φ=l/ρ，ρ =r/sin2θ，則

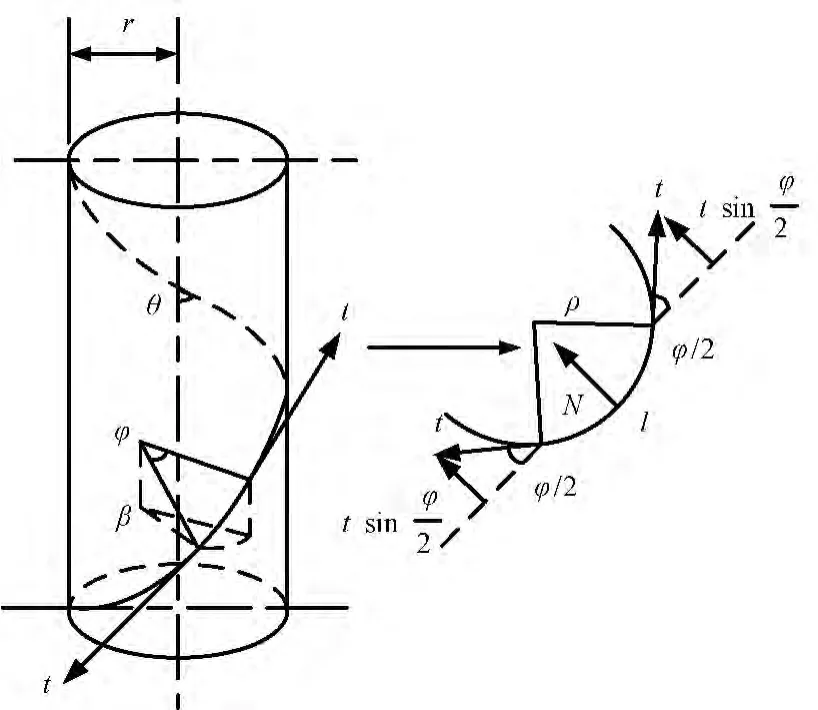
圖3 單紗對紗線向心壓力的分解Fig.3 Centripetal force decomposition

式中，t為所受張力，φ為包圍角，r為離軸線距離，β為橫截面上l轉過的角度。

在本文研究中，t=Ttcosθ/2，β=π，則

將各個關系代入式(1)，則模型的最終表達式為:

3 分析與討論

根據式(13)可看出，等式右邊具體參數為單紗半徑rf、股線捻回角 θ、拉伸應變 εy、抱合系數 α、單紗拉伸模量Y、單紗剪切模量K。關于參數對最終股線總強力的影響分析如下。

3.1 拉伸與剪切模量的影響

據式(13)所知，單紗模量對股線總強力的影響是體現在股線拉伸模量Ey上的，而Ey/Y為股線與單紗的模量比，體現單紗雙股捻合后整體模量的變化，所以比較不同拉伸模量Y和剪切模量K對Ey/Y的影響即可，4種不同材料的模量屬性見表1。在式(6)中，捻回角θ取π/12，經由MatLab計算并繪圖結果如圖4所示。從圖中可看出，單紗加捻成股線結構后，整體拉伸模量會有一定比例的減小。結果顯示，在捻回角相同的情況下，不同材料組成的單紗拉伸模量與剪切模量的比值越大，其總體模量減小的比例越大，則對應合股的紗線的抗拉能力則越差。

表1 材料屬性Tab.1 Material properties

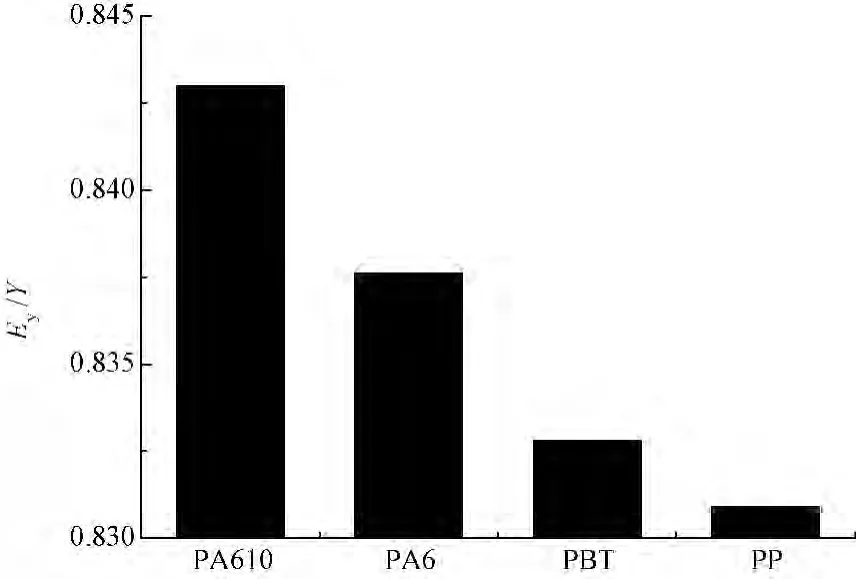
圖4 股線單紗模量之比與材料的關系Fig.4 Relationship between material type and modulus ratio of ply yarn and single yarn

3.2 細密度的影響

紗線的強力一般與其細密度呈正相關趨勢，即細密度越大，截面范圍內能承受的纖維根數越多，則紗線強力越高。而化纖單紗支數與其直徑的表達式［13］如下:

式中，df為單紗直徑，δ為單紗密度，Ne為英制支數。由式(13)可知，股線強力隨單紗直徑的平方呈線性增加關系，結合上式可得出，紗線的強力與單紗的支數呈簡單的反比關系，符合一般認識。

3.3 抱合系數的影響

抱合系數用來反映纖維之間抱合程度的參數，據式(5)可計算單紗之間的摩擦力。在紡織紗線領域，一般系數取值為0.4～0.6［10］。本文研究考慮了2根單紗界面摩擦力的因素，即在拉伸過程中界面存在相對滑動的趨勢(未發(fā)生相互滑移的情況下)。圖5示出不同抱合系數對股線總強力的影響情況(材料為 PA6，直徑為0.2591 mm，由式(14)確定，應變取0.25，捻回角為π/12)。

圖5 抱合系數與總強力的關系Fig.5 Relationship between cohesion factor and total strength

經由MatLab計算并繪圖結果顯示，抱合系數對股線強力的影響是正相關的，即抱合系數α越大，單紗之間的摩擦力越大，最終體現在對總強力的貢獻越大，所占比例較拉伸部分影響較小，最大情況下不超過總強力的10%。

3.4 捻回角的影響

加捻是股線增強效應最主要的因素，而捻回角的大小是描述加捻程度的客觀指標。以雙股線材料PA6，直徑為0.2591 mm，應變0.25為例，描述股線強力、拉伸力和摩擦力隨捻回角增加的變化情況，經由MatLab計算并繪圖，結果如圖6所示。

圖6 總強力、拉伸力和摩擦力隨捻回角的變化情況Fig.6 Total strength，tensile strength and friction changes along with ply yarn's twist angle

結果表明:拉伸力隨著捻回角的增大，股線總體拉伸模量不斷減小，而摩擦力則從0開始逐漸增大，在31°附近達到最大，隨后逐漸減小;而當捻回角在12°附近時，股線的強力出現極大值，這類似于單紗加捻時會出現臨界捻系數，此現象在此也得到了證明。最終對捻度增強效應的解釋為:若只考慮軸向力的影響，捻度的改變對強力無增強作用;若將由于加捻作用引起的單紗間摩擦力考慮進來，則在加捻到一定程度之前，總強力會有一定的增強效果，并可從公式關系上定量確定雙股線的臨界捻系數大小。

3.5 單紗變化的影響

3.1 小節(jié)只討論了單紗的變化對股線拉伸模量的影響關系，若將這種關系放寬到影響整體股線強力時，類似于3.4中只討論一種材料，結合式(6)、(14)，及表1中的單紗材料屬性，經由MatLab計算并繪圖給出了當抱合系數為0.5時，同一應變下(0.25)其強力隨捻回角的變化情況，如圖7所示。

圖7 單紗變化對總強力的影響Fig.7 Effect of single yarn types on total strength

結果顯示，4種不同材料組成的股線總強力都呈現出如圖6所示的趨勢，即隨著加捻程度的加大，單紗之間抱合力的增加趨勢大于因單紗取向分力減小的趨勢，其總體強力會呈現出增大的趨勢，但隨著取向角度不斷增大，摩擦力也呈現出如圖6的衰減趨勢，而取向分力下降趨勢更加顯著，其結果導致總強力出現極大值后的不斷減小。

通過上述研究發(fā)現，單紗的性質和股線的結構共同決定著股線的性質，本文研究采用較少的可調參數推導了關于雙股線強力的數學模型，能用來量化解釋股線中的單紗和股線結構對其總強力的影響情況，參數包括單紗半徑rf、股線捻回角θ、拉伸應變εy、抱合系數α、單紗拉伸模量Y、單紗剪切模量K，這些參數與整體股線的強力有著密切的關系。而最終的模型也能夠用來分析已生產的成品股線性能，可用來描繪單紗的變化對股線拉伸行為的影響，通過單紗模量及其他參數可用來預測加捻過程中股線達到最大強力時的捻度水平，同時可量化分析單紗的變化對股線強力的影響情況。

4 結論與展望

本文研究從雙股線模型的幾何配置出發(fā)，認為股線捻度的變化及單紗之間作用力共同決定了股線的強力，經研究與推導發(fā)現如下關系及結論:1)在理想紗線模型的基礎上，建立了雙股線理想模型的幾何配置，并給出模型的假設條件;2)分析了單紗短片段在拉伸載荷下軸向和徑向的力學狀態(tài)對拉伸行為的作用后，得出其拉伸模量上與單紗模量的關系式;3)將單紗之間的抱合力考慮為組成股線強力的一部分，推導了在單紗無滑移情況下股線強力的表達式，定量分析討論了單紗性能參數及加捻程度對股線最大強力的影響情況;4)最終模型能夠用來分析成品股線性能;描繪單紗變化對股線拉伸行為和產品強力的影響;通過較少的參數就可用來預測加捻過程中股線達到最大強力時的捻度水平。

將來進一步的研究將考慮初始預應力及加捻引起的捻縮現象對單紗及最終強力的影響;將單紗具體化為束纖維、加捻長絲紗或短纖紗;在實驗驗證與修正方面的工作，也會同期進行。

［1］ CORBMAN B P.Textile，Fiber to Fabric［M］.6nd ed.New York:McGraw-Hill Book Co，1983:Chapter 3.

［2］ RIDDLE E R.Preliminary considerations in a plan of work to develop fiber-yarn models ［C］//Proc Engineered fiber selection mini conference.Raleigh:Raleigh cotton incorporated，1988:161.

［3］ PLATT M M.Mechanics of elastic performance of textile materials:part III:some aspects of stress analysis of textile structures-continuous-filament yarns［J］.Text Res J，1950，20:1－15.

［4］ PLATT M M.Mechanics of elastic performance of textile materials:part IV:some aspects of stress analysis of textile structures-staple fiber yarns［J］.Text Res J，1950，20:51.

［5］ HEARLE JWS， GROSBERGP， BACKERS.Structural Mechanics of Fibers， Yarns and Fabrics［M］.New York:John Wiley ＆ Son Inc，1969:175－207.

［6］ NACHANE R P，KRISHNA IYER K R.Yarn tension as a function of extension:a new approach［J］.Text Res J，1987，57:279 －282.

［7］ NACHANE R P. Yarntensionasafunctionof extension:anew approach-application to an ideal twisted multifilament yarn［J］.Text Res J，1990，60:128－136.

［8］ 聶毓洪，袁斌鈺.股線中單紗幾何配置和股線強力的力學分析［J］.紡織學報，2006，27(7):19－22.NIE Yuhong，YUAN Binjue.Geometric disposition of the single yarns and mechanical analysis of strength in ply yarn［J］.Journal of Textile Research，2006，27(7):19－22.

［9］ PALANISWAMY N K，PEER Mohamond A.Effect of single yarn twist and ply to single yarn twist ratio on strength and elongation of ply yarns［J］.Journal of Applied Polymer Science.2008，98(5):2245－2252.

［10］ 安降龍，郁崇文.賽絡紡復合紗線結構及其拉伸力學模型［J］.東華大學學報:自然科學版，2010，36(1):15－20，25.AN Xianglong，YU Chongwen.Mechanical model of sirospun composite yarn［J］. Journal of Donghua University:Natural Science Edition，2010，36(1):15－20，25.

［11］ 任家智.紡紗原理［M］.北京:中國紡織出版社，2002:133.REN Jiazhi.Principles of Spinning［M］.Beijing:China Textile＆ Apparel Press，2002:133.