基于最小二乘法和遞推最小二乘法的雷達伺服跟蹤系統建模
李 紅(1.合肥工業大學,安徽合肥 230009;2.中國電子科技集團公司第38研究所,安徽合肥 230088)
?
基于最小二乘法和遞推最小二乘法的雷達伺服跟蹤系統建模
李紅1,2
(1.合肥工業大學,安徽合肥230009;2.中國電子科技集團公司第38研究所,安徽合肥230088)
摘要:雷達伺服轉臺的精確建模是實現高性能控制的基礎,傳統的機理建模準確性有待提高。設計并實現了雷達伺服轉臺的系統辨識實驗,對所得現場數據應用最小二乘(Least Squares)和遞推最小二乘算法(Recursive Least Squares algorithms),獲得雷達伺服轉臺的傳遞函數模型。
關鍵詞:雷達;伺服系統;系統建模;最小二乘算法
0 緒論
雷達伺服系統作為雷達的重要組成部分,是一種精密伺服系統,其技術水平的高低直接影響到跟蹤精度乃至整個雷達的性能。對系統的模型結構和參數有確定的認知是實現對被控對象的精確控制的基礎。目前對雷達伺服系統進行建模,多采用機理建模,此方法的優點是思路清晰、理論成熟[1-3]。但由于轉動慣量、摩擦、齒輪間隙等結構因素的影響[4],機理建模所得模型與實際系統有較大出入;另外投入使用后設備會在各方面發生很大變化,理論數據的可靠性將值得質疑。文[5]以機理建模的方法得到雷達伺服系統穩定平臺直流力矩電機驅動器的結構框圖;文[6]列寫電壓方程、運動方程、轉矩方程,可得到各個軸的傳遞函數。本文在機理建模的基礎上,對雷達三軸穩定平臺進行系統辨識建模,建立離散脈沖傳遞函數描述系統的輸入輸出關系。
1 辨識算法的基本原理
1.1最小二乘法
最小二乘類參數辨識方法包括最小二乘及其他改進算法,其中最小二乘法最基本,應用廣泛。本文以雷達伺服轉臺的方位角度控制系統為研究對象,對該單輸入單輸出(Single Input Sin?gle Output,SISO)系統進行建模和參數辨識研究,如圖1所示。
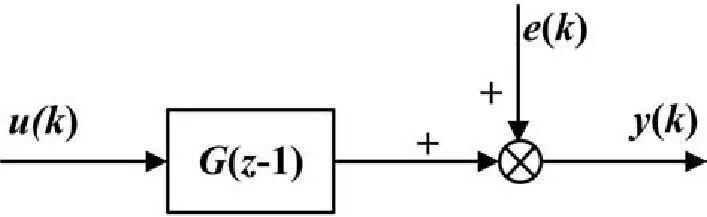
圖1 SISO過程的辨識
記錄可測的輸入u(k)和輸出y(k)數據序列;用過程模型,即脈沖傳遞函數G(z-1)用來描述過程的輸入輸出特性,通常,其中A(z-1)和B(z-1)分別為階數na,nb的多項式。不確定因素的影響歸結為附加噪聲e(k),則
A(z-1)y(k)=B(z-1)u(k)+e(k),變成最小二乘格式y(k)=h'(k)θ+e(k),其中:
h(k)=[-y(k-1),…,-y(k-na),u(k-1),…,u(k-nb)]'
θ=[a1,a2,…,ana,b1,b2,…,bnb]'
對于k=1,2,3,…,L,方程構成線性方程組,寫作yL=HLθ+eL
yL=[y(1),y(2),…,y(L)]',eL=[e(1),e(2),…,e(L)]'。
對于ARX模型,取準則函數J(θ):
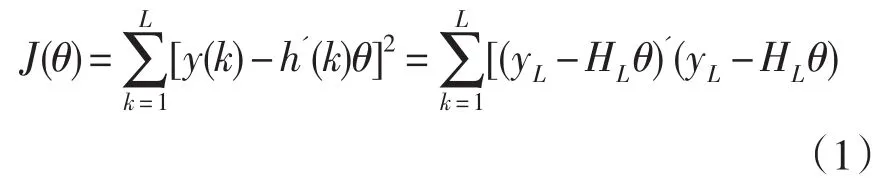

1.2遞推最小二乘法
最小二乘法遞推算法RLS(recursive least squares)的基本思想可以概括成[9]:當前估計值?(k ) =上一步估計值?(k+1 ) +當前修正值。
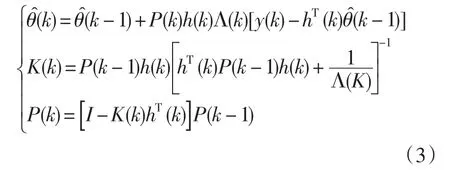
計算過程中可能出現舍入誤差,為了保證p(k)的對稱性,有時把上組式子中的第三式寫為:
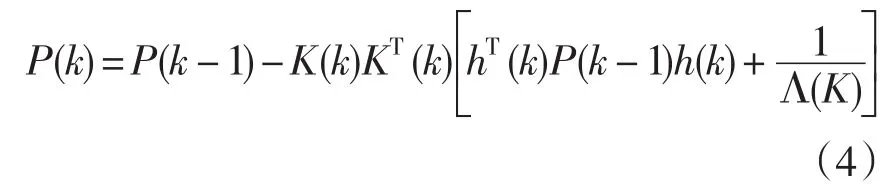
遞推計算需要事先選定初始參數θ?(0)和P(0),可根據一批數據利用一次性完成算法預先求得,也可直接取:
P(0)=α2I,α為充分大的實數,?(0)=ε,ε為充分小的實向量。(5)
2 辨識試驗的設計
2.1先驗知識的獲取
作為常見的軍用產品,雷達伺服系統的非線性一般在設計的過程中即被嚴格控制,并采用電流負反饋環路、高精度線性檢測元件等手段克服其非線性的影響。所以本系統的非線性程度降到了最低程度。同上原因,可認為本系統是SISO的線性時不變系統。表1寫出了原有系統的各重要性能指標。
2.2輸入信號的選擇
為了滿足參數辨識和建模的要求,輸入信號必定存在一定的約束條件。首先,在辨識時間內雷達伺服系統的過程動態必須被輸入信號持續激勵,或者說,在實驗期間輸入信號必須充分激勵過程的所有模態[9]。其次,為了避免進入非線性區,輸入信號的幅度或功率幅度不宜過大;但也不能太小,以免數據所含的信息量下降,直接影響辨識的精度。實驗初期采用的是幅值為3°的階躍,但在應用最小二乘法(1)式進行辨識時,出現病態矩陣無法求逆,可用最小二乘的遞推算法進行求解。本實驗選擇了偽隨機信號M序列(線性移位寄存器序列)作為辨識輸入信號。將4級移位寄存器輸出的邏輯0和邏輯1變換成3°和-3°的階躍序列,如圖2所示。
2.3采樣時間和辨識時間的選取
對連續時間進程進行辨識時,輸入輸出信號需經過采樣處理。采樣時間的選擇直接影響辨識模型的結構與精度,除需滿足采樣定理外,必須統籌考慮控制器精度、計算和存儲能力、辨識算法計算時間、執行機構響應速度等因素。本文系統辨識試驗中選取的采樣時間為0.01秒。
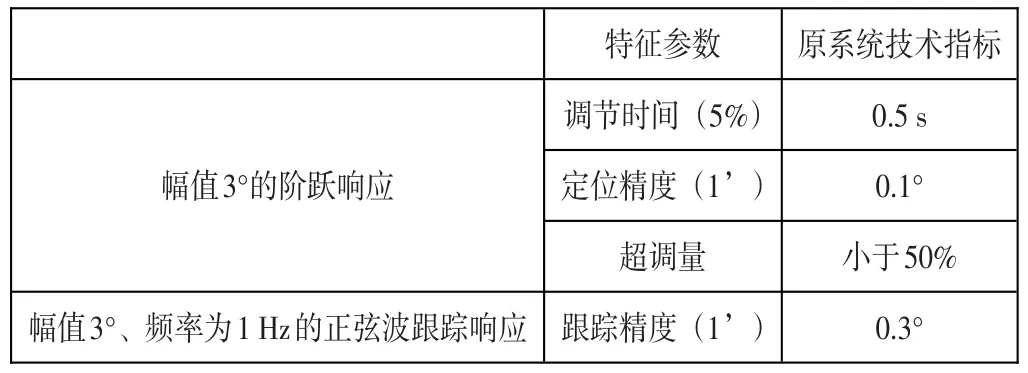
表1 原系統的階躍響應技術指標
辨識時間的選取即數據長度的選定。現有系統的調整時間為0.5秒,即階躍響應0.5秒后,系統基本處于穩定狀態。考慮到留有余地、數據錄取系統的方便性及適應具體辨識算法,辨識時間初步選定為12秒,其中前2秒為階躍前零過程,后10秒為階躍響應過程。
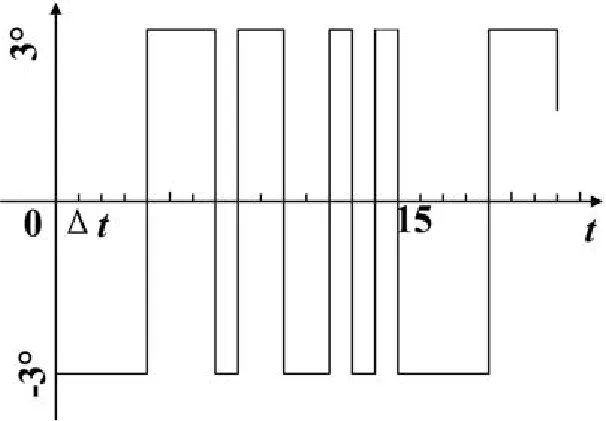
圖2 4級M序列變換成幅值為3°和-3°的序列
3 雷達伺服跟蹤系統結構介紹[5]
機載SAR穩定平臺直流力矩電機驅動器由位置環、穩定環、速度環和電流環的四閉環系統共同組成。雷達伺服系統中,速度環路是一個重要的內環路,它不僅能夠提高系統的低速平穩性,擴大系統的調速范圍,且能夠增強系統抵抗負載擾動的能力。
4 辨識結果
雷達伺服轉臺的傳遞函數模型結構如下:
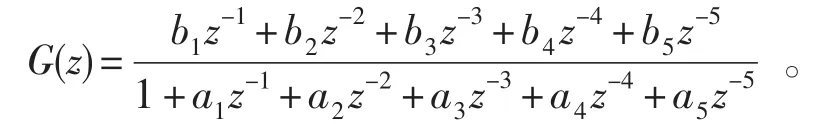
4.1最小二乘法辨識結果
輸入為M序列一次完成最小二乘的辨識結果:a1=-4.031 0,a2=6.621 0,a3=-5.631 0,a4=2.523 0,a5=-0.481 4,b1=0.010 5,b2=0.013 8,b3=-0.050 4,b4=0.018 9,b4=0.007 2。
4.2遞推最小二乘法辨識結果
最小二乘一次完成算法占用大量內存,不適合在線辨識。為減少計算量及所占數據存儲量,應用遞推最小二乘參數的辨識過程如圖3所示。初始值直接按式(5)選定,最終輸出結果:a1=-4.016 3,a2=6.573 7,a3=-5.572 3,a4=2.488 6,a5=-0.473 6,b1=0.010 5,b2=0.013 9,b3=-0.050 0,b4=0.018 4,b4=0.007 1。
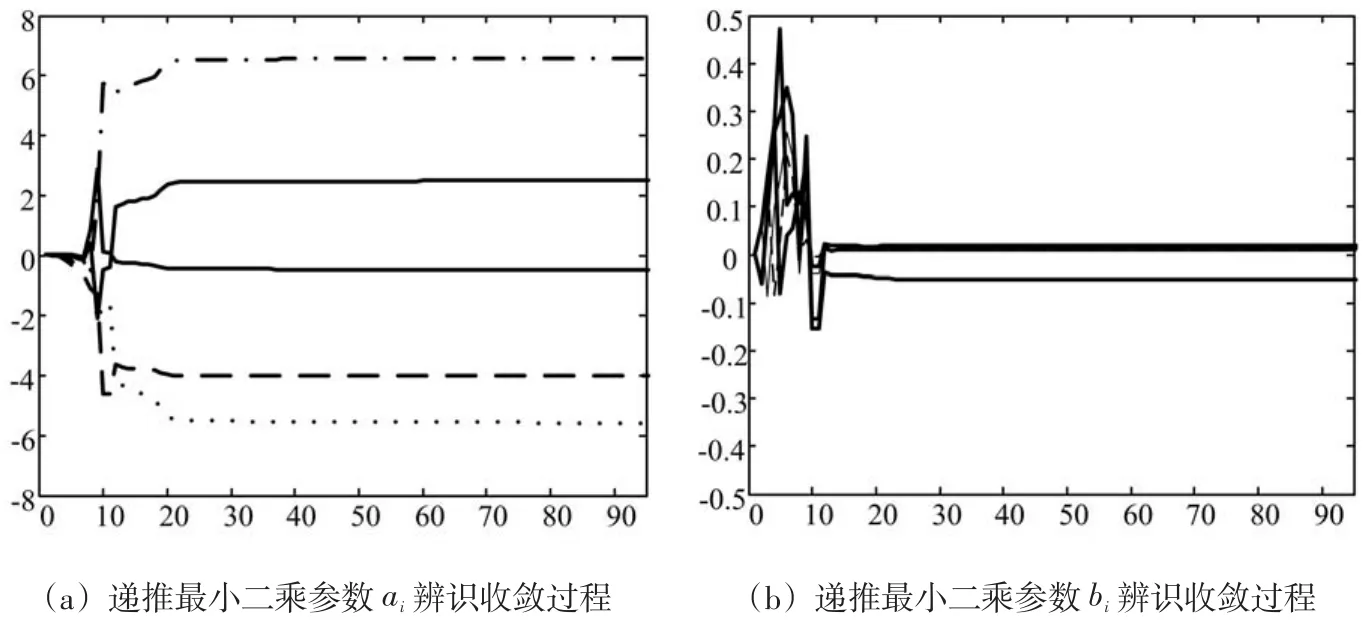
圖3 遞推最小二乘參數的辨識
5 結論
本文設計并實現了雷達伺服轉臺的系統辨識實驗,對輸入輸出現場數據應用最小二乘算法和遞推最小二乘算法進行處理,在機理分析的基礎上對雷達伺服系統進行參數辨識建模,獲得其五階線性脈沖傳遞函數模型。該模型可真實的反應雷達伺服系統的輸入輸出關系,為精確的控制器設計奠定基礎,為提高雷達跟蹤性能創造了理論條件。
參考文獻:
[1]潘高峰,周江.船載雷達伺服系統的建模與仿真[J].電子工程師,2007,33(6):7-9.
[2]李蘭,房建成,韓潮.基于SIMULINK的慣性平臺穩定系統的建模與仿真[J].中國慣性技術學報,2005,13(2):19-23.
[3]薛輝,李萍.基于MCU+EPLD的雷達天線轉臺通用伺服系統設計[[J].機電工程技術,2013(7):60-62.
[4]李正大,陳光達,馬洪波.結構因素對雷達伺服系統性能影響及其測試研究[J].現代電子技術,2008,266(3):33-36.
[5]王振收.機載SAR穩定平臺直流力矩電機驅動器[J].現代雷達,2006,28(3):70-75.
[6]熊峰.機載雷達伺服系統研究與仿真[J].電訊技術,2003(2):1-4.
[7]·I lyas Eker,Open-loop and closed-loop experimental on-line identification of a three-mass electromechanical system,Mechatronics[J]. 2004(14):549-565.
[8]Ivan Markovsky,Sabine Van Huffel,Overviewoftotal least-squares methods[J]. Sig?nal Processing,2007(87):2283-2302.
[9]侯媛彬,汪梅,王立琦.系統辨識及其MATLAB仿真[M].北京:科學出版社,2004.
(編輯:阮毅)
The Identification and Simulation of Radar Servo-System Based on the Least Squares Method and Recursive Least Squares
LI Hong1,2
(1. Hefei University of Technology,Hefei230009,China;2. The 38th Research Institute of CETC,Hefei230088,China)
Abstract:The precise modeling of the radar servo system is the basis of high performance controller. The precision of traditional mechanism model needs to be improved. Based on the system identification theory,the Least Squares and Recursive Least Squares algorithms are used to obtain transfer function model of the radar servo system.
Key words:radar;servo system;system identification;least squares algorithm
作者簡介:李紅,男,1980年生,碩士研究生,高級工程師。研究領域:天線伺服系統、穩定平臺和機載環境控制系統。已發表論文4篇。
收稿日期:2015-05-12
DOI:10. 3969 / j. issn. 1009-9492. 2015. 11. 006
中圖分類號:TN953
文獻標識碼:A
文章編號:1009-9492 ( 2015 ) 11-0023-03

