磁懸浮開關磁阻電機懸浮系統自抗擾逆系統解耦控制

李雪林，孫玉坤

(1.江蘇聯合職業技術學院 揚州商務分院，揚州225001;2.江蘇大學，鎮江212013)

0 引 言

開關磁阻電動機可以在極速、低功耗的條件下運行，但是電機在極速下運行的主要問題是電機的機械軸承容易磨損，機械摩擦會使轉子承受很大的摩擦阻力，并且會使電機相關部件發熱，發熱到一定程度時會使電機氣隙變得不再均勻，從而破壞電機的動態特性，電機的效率降低，影響并減少電機及裝備的使用年限［1］。為應對此問題，日本電機研究專家展開了磁懸浮開關磁阻電動機(以下簡稱BSRM)相關技術的探究。BSRM 的特點是沒有特殊的機械軸承來支撐轉子，而是通過磁懸浮技術將轉子運行在穩定的懸浮狀態［2-5］，將機械磨損這個電機軸承常見的問題解決了。

電機轉子的懸浮保持穩定是BSRM 研究的關鍵，其中包括懸浮控制的非線性耦合和徑向兩自由度上的耦合及轉矩調節這兩方面研究，迄今為止，在軸承徑向上的相關解耦研究已有初步的進展［6-8］，但這些研究均設定電機主繞組電流ima為一常數，把轉矩設定在運行于理想狀態。事實上，轉矩動態變化一直在進行，由此，怎樣讓轉矩動態變化時電機ima的攝動對懸浮系統的穩定運行與控制不產生影響，是一個亟待解決的問題。

神經網絡系統的優點是非線性逼近能力和容錯性，將此應用在對懸浮系統與轉矩之間解耦研究中［9］，但神經網絡的缺點是訓練繁瑣復雜。本文對懸浮系統解耦時采用逆系統的簡便特點，再利用自抗擾控制器對被控對象數學模型的不依賴特性和優秀的抗干擾能力［10-12］，設計了BSRM 懸浮系統的自抗擾逆系統解耦控制方法。該方法將主繞組電流的攝動視為懸浮系統的外擾，將懸浮系統用逆系統反饋線性化進行解耦，使其成為兩個相對獨立的子系統，最后采用自抗擾控制器(以下簡稱ADRC)作為徑向位置控制器對復合偽線性系統進行綜合，擴張狀態器對主繞組電流的攝動進行實時補償，從而把轉矩動態變化對懸浮控制的干擾消除，使懸浮系統穩定運行。該控制策略的有效性和可行性得到了仿真試驗驗證。

1 磁懸浮開關磁阻電機懸浮系統控制模型

設磁懸浮開關磁阻電機轉子的α 方向的徑向位置為xα，β 方向的徑向位置分別xβ;設ima為主繞組電流;isa1和isa2為 徑向力繞組電流。轉子的徑向力公式如下［6］:

式中:Kf1，Kf2表示系統兩個懸浮力系數，由磁懸浮開關磁阻電機實際參數代表，表達式參見文獻［6］。

由牛頓第二定律得出轉子在徑向力方向下的控制模型表達式:

式中:m 為轉子質量;mg 為轉子所受重力。

把式(1)代入式(2)，徑向力控制模型改寫:

根據式(3)可知，系統是復雜的有兩個輸入和兩個輸出的強耦合系統。

2 磁懸浮開關磁阻電機懸浮系統控制模型的解析逆系統

對于改寫的徑向力控制模型式(3)，設定狀態變量:

且

輸入系統變量:

且

輸出系統變量:

且從而得出系統的狀態方程和輸出方程分別為:

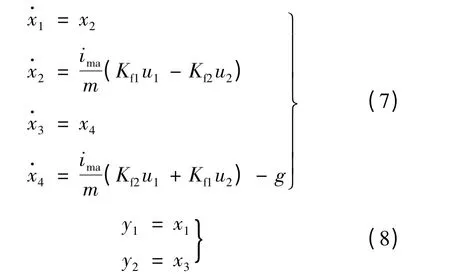
利用可逆性對模型進行分析，利用求導對輸出方程進行運算，使方程中出現輸入變量。再通過式(7)和式(8)推得:

其Jacobi 矩陣:

根據rank=2，得出矩陣A 是非奇異矩陣，由階數α=(2，2)，2 +2 =4，由于系統是4 階矩陣，從而系統是可逆的。

將逆系統理論的狀態反饋線性化方法應用于系統，令:

求解式(11)，得到狀態反饋算法:

通過式(12)所表達的系統狀態的反饋關系，由磁懸浮開關磁阻電機徑向力的控制式(3)可推出無耦合偽線性系統:

3 懸浮系統的ADRC 逆系統解耦控制

3.1 ADRC 的結構及工作原理

自抗擾控制器對被控對象不需要精確的數學模型，對被控對象模型攝動和外界干擾的疊加進行實時估算，并動態補償的一種非線性控制器，跟蹤微分器(TD)和擴張狀態觀測器(ESO)及非線性狀態誤差反饋(NLSEF)是自抗擾控制器(ADRC)的三個主要部分。常設定二階受控系統作示例，圖1 為ADRC 的結構［10］。

圖1 自抗擾控制器結構框圖

跟蹤微分器的作用是產生過渡過程然后選出其各階微分信號，即此過程中y*(t)會產生1 個輸出v1(t)和另1 個輸出v1(t)的微分信號v2(t)。y*(t)的跟蹤信號是v1(t)，這是一個光滑過渡過程。

y(t)對擴張狀態觀測器產生信號1 z1(t)，信號2 z2(t)，信號3 z3(t)，可以看出y(t)的跟蹤信號為信號1 z1(t)，信號1 z1(t)的微分信號為信號2 z2(t)，對系統模型攝動和外界干擾疊加的估算為信號3 z3(t)，對擾動起補償作用的是z3(t)/b 的反饋。

非線性狀態誤差反饋利用z1(t)與v1(t)的誤差e1(t)及z2(t)與v2(t)的誤差e2(t)來產生控制信號u0(t)，u0(t)與z3(t)/b 相減形成最終控制量u(t)。

3.2 ADRC 逆系統解耦控制

由式(13)可以判斷，系統經解耦和線性化后，磁懸浮開關磁阻電機懸浮系統在徑向上取得了控制的獨立性，然而主繞組電流ima產生的干擾卻沒有有效去除，并且主繞組電流的干擾具有不確定性;另外，外力擾動對懸浮系統控制有無法忽略的影響。所以，對系統懸浮系統采用自抗擾控制來設計控制算法，把主繞組電流ima引起的攝動視為系統的一種外擾，利用ESO 進行實時補償。由于懸浮系統經逆系統方法反饋線性化為兩個相對獨立的偽線性子系統，因而把ima引起的攝動影響分為兩部分，用w1(ima)和w2(ima)分別表示攝動對兩個獨立子系統的影響，控制系統結構如圖2 所示。

由于徑向位置兩自由度對稱，以x*α自由度為例，給出自抗擾控制器各部分算法如下:

TD 方程:

圖2 BSRM 的自抗擾逆系統解耦控制結構圖

ESO 方程:

式中:

α1，α2，α3，δ2，bα，bt01，bt02，bt03為可調參數。

NLSEF 方程:

式中:α4，α5，δ3，bt1，bt2為可調參數。

4 仿真試驗研究

以磁懸浮開關磁阻電動機實驗機為仿真對象，利用仿真軟件MATLAB 中Simulink 及模糊邏輯工具箱進行控制系統的解耦仿真試驗。實驗機各相關參數如表1 所示。

表1 BSRM 參數

4.1 控制系統性能試驗和解耦分析

為驗證系統的控制性能，對電機轉子的起浮過程進行研究，設定轉子α 軸徑向起始位移為-20 μm，圖3 為α 軸徑向位移起浮特性圖。由仿真分析可知，系統沒有超調，動態響應快，調節迅速，顯示良好的動態性能。

圖3 α 軸徑向位移起浮特性圖

為進一步檢驗解耦控制的性能，系統設定不同的時刻進行變化，在初始時刻t=0 時徑向α 軸位移給定從-18 μm 變化到0，t=3 ms 時徑向β 軸位移給定從0 變化到20 μm，其解耦控制效果由圖4(a)和4(b)所示。從而判定一個輸出只受一個輸入影響，相互沒有影響，動態解耦性能非常好。

圖4 自抗擾逆系統解耦控制效果

4.2 ima攝動試驗

設定磁懸浮開關磁阻電動機主繞組電流ima由5 A 變5.5 A，顯然，系統模型將出現較大擾動。圖5為ima變化后徑向α 軸位移起浮特性圖。對比圖3可見，在ima發生較大攝動后，徑向α 軸位移起浮特性曲線幾乎沒有變化，從而驗證了自抗擾控制器突出的抗干擾特性，說明利用非線性自抗擾控制能夠消除數學模型和系統參數的攝動。該試驗同時間接驗證了自抗擾逆系統解耦控制策略解耦效果不依賴于被控制對象數學模型的特性。

圖5 ima變化后徑向α 軸位移起浮特性

5 結 語

自抗擾控制器是一種新型的不依賴于被控制對象數學模型的非線性控制器，具有很強的魯棒性和抗干擾性。結合自抗擾控制和逆系統方法的優點，利用自抗擾控制器來消除系統數學模型和參數的攝動，逆系統方法來進行解耦線性化，設計了BSRM 系統的自抗擾逆系統解耦控制策略。仿真結果驗證了該控制策略的有效性。本文研究可知，為了消除逆系統方法依賴于被控制對象精確數學模型的缺點，可以采用一些合適的不依賴于被控制對象數學模型、對模型攝動具有較強適應性的非線性控制器與逆系統方法相結合，對BSRM 系統進行解耦控制。

［1］ 謝寶昌，任永德. 磁懸浮電機及其應用的發展趨勢［J］. 微電機，1999，32(6):28 -30.

［2］ 竹本，鈴木.改進的無軸承開關磁阻電動機的分析［C］//International Conference IEMD’99，1999:773 -775.

［3］ 竹本，千葉.一種新的無軸承開關磁阻電機采用方波電流控制方法［C］//IEEE 電力工程協會冬季會議，2000(1):375 -380.

［4］ 竹本，千葉.無軸承開關磁阻電機的確定方波電流超前角的方法［J］.IEEE 工業應用，2001，37(6):1702 -1709.

［5］ 竹本，千葉.前饋減振補償無軸承磁開關磁阻電動機［C］//第七國際研討會，2000:395 -400.

［6］ 劉羨飛，孫玉坤，磁懸浮開關磁阻電機徑向位置解耦及仿真研究［J］.系統仿真學報，2007，19(7):1527 -1530.

［7］ 李雪林，孫玉坤，磁懸浮開關磁阻電機模糊補償逆系統解耦控制［J］.電機與控制應用，2009(5):16 -20.

［8］ 張 亮，孫玉坤，基于微分幾何的磁懸浮開關磁阻電機徑向力的變結構控制［J］.中國電機工程學報，2006，26(19):121 -126.

［9］ 孫玉坤，任元.BSRM 懸浮力與旋轉力的神經網絡逆解耦控制［J］.中國電機工程學報，2008，28(9):81 -85.

［10］ 韓京清. 自抗擾控制器及其應用［J］. 控制與決策，1998，13(1):19 -23.

［11］ 韓京清. 從PID 技術到“自抗擾控制”技術［J］. 控制工程，2002，9(3):13 -18.

［12］ 黃一，張文革.自抗擾控制器的發展［J］. 控制理論與應用.2002，19(4):485 -492.