基于二次小波去噪的FastICA盲源分離研究*

趙 奎 黃高明

(海軍工程大學電子工程學院 武漢 430033)

?

基于二次小波去噪的FastICA盲源分離研究*

趙 奎 黃高明

(海軍工程大學電子工程學院 武漢 430033)

論文針對含噪聲混合信號分離問題,提出了三步處理法,首先采用小波濾波進行去噪處理,再采用快速獨立分量分析(FastICA)盲源分離技術實現混合信號的分離,最后對分離后的信號二次使用小波濾波處理。仿真實驗結果表明,該方法能夠很好地分離含噪混合信號,從分離前后的波形及平均信噪比對照,去噪性能和分離效果良好。

小波濾波; 獨立分量分析; 波形; 平均信噪比

Class Number TN911

1 引言

盲源分離(Blind Sources Separation,BSS)技術是20世紀90年代中后期迅速發展起來的一種功能強大的信號處理方法,在不能應用參考信號或信號模型的前提下估計出原始信號。盲源分離作為人工神經網絡、統計信號處理、信息理論相結合的產物,現已成為眾多領域中研究與發展的重要課題,特別是在生物醫學、語音與通信、圖像處理、地球科學、計量經濟學、文本數據挖掘等方面均有突出貢獻[1]。

FastICA的盲源分離技術即是從觀測到的混合信號中提取、恢復出無法直接觀測的每個原始信號的過程,“盲”即是指源信號未知,并且混合系統特性也未知或是僅知道其少量先驗知識(如非高斯性、循環平穩性、統計獨立性)這兩方面。該技術更適合于復雜電磁環境下的信號分離。傳統的ICA算法在解決無噪或低噪情況下的混疊時,分離性能很優越,但當噪聲較大時,分離效果則不好。

然而,復雜電磁環境下的信號往往是疊加有噪聲的,小波變換可以將原始混合信號分解為一系列的近似分量和細節分量,信號噪聲主要表現在信號的細節分量上。使用一定的閾值處理細節分量后,再經過小波重構就可以得到較平滑的與原始信號近似的信號。本文使用小波變換對各帶噪混合信號進行預去噪處理,然后用FastICA的方法對去噪后的混合信號進行分離,最后再進行一次去噪處理,最終得到各個信號。仿真結果表明,此方法取得了較好帶噪混疊信號分離。

2 帶噪混疊信號模型

根據背景噪聲與信號關系,噪聲可分為加性噪聲和非加性噪聲。對于某些非加性噪聲而言,可以通過相關變換轉換為加性噪聲。例如,某些與信號相關的量化噪聲可以通過偽隨機噪聲擾動的方法轉換為與信號獨立的加性噪聲。

信號處理中的加性噪聲可以分為周期噪聲、脈沖噪聲、寬帶噪聲等,寬帶噪聲來源廣泛,它和信號在時域和頻域上都基本重合,只有在沒有信號階段,噪聲分量才單獨存在,因此對噪聲的消除比較困難[2]。

論文中考慮的帶噪混疊信號中的噪聲均視為加性寬帶高斯白噪聲,其線性瞬時混疊信號模型為

x(t)=As(t)+n(t)

(1)

其中,x(t)=[x1(t),x2(t),…,xm(t)]T為m維觀測信號;s(t)=[s1(t),s2(t),…,sm(t)]T是m維未知信號;A為未知混疊方陣;n(t)=[n1(t),n2(t),…,nm(t)]T為m維加性高斯白噪聲。

3 分離過程

整個過程中,首先利用小波變換對帶噪混疊信號xm(t)進行去噪處理,得到盡量“純凈”的信號ym(t)。然后對ym(t)進行去均值和預白化處理,再采用FastICA算法對去噪后并預處理的混合信號進行分離,得到分離信號,此時,再次應用小波濾波對分離后的信號進行濾波處理。

圖1 分離流程圖

3.1 小波去噪處理

小波變換具有多分辨率的特點,在時域和頻域都具有表征信號局部特征的能力,適合分析非平穩信號。

在小波去噪處理中需要注意以下問題[3]:

1) 處理方法。軟閾值法和硬閾值法是小波消噪閾值處理的兩種方法。其中軟閾值處理方法能夠使估計信號具有和原始信號同樣的光滑性,并且獲得的信號不會產生附加振蕩;而硬閾值處理方法通常會使估計信號產生振蕩,并且信號欠光滑性。

2) 閾值選取。噪聲是一種隨機信號,其方差未知,實際去噪過程中必須先對閾值進行估計,閾值估計方法有:(1)固定閾值(sqtwolog)選擇;(2)基于史坦(Stein)的無偏釋然估計原理的自適應閾值選擇;(3)啟發式閾值選擇;(4)極大極小閾值選擇。

3) 小波基選擇。小波函數具有多樣性,經驗與理論的分析表明,去噪的效果隨著小波函數的變化而改變,信號的效果與小波函數的正則性及基函數波形與數據的結構相似程度有關。對稱性好的小波不產生相位畸變,正則性好的小波易于獲得光滑的重構曲線和圖像,選擇對稱性和正則性均較好的小波系進行去噪能得到更好的去噪效果。

4) 小波分解層數確定。不同分解層數去噪效果不一樣,合理選擇分解層數。

此文中采用基于對稱延拓法小波進行三層分解并用啟發式軟閾值進行小波系數閾值化處理。啟發式軟閾值法去噪更加徹底,能夠將混疊噪聲有效濾除,而且估計信號具有和原始信號相同的光滑性,并且得到的信號不會產生附加振蕩。

3.2 快速獨立分量分析算法

快速獨立分量分析(FastICA)算法的計算過程運用了批處理的方法,但計算時運用了自適應處理方法,可以說是兩種方法的結合。每次分離只提取一個源信號,接著將其從原始數據中去掉,然后對剩下的數據進行下一輪提取,可以采用Gram-Schmidt正交分解來實現。

對所有ICA問題都要作一定的假設和約束:

1) 源信號si(i=1,2,…,m)都是零均值的實隨機變量,且在任意時刻相互統計獨立。

2) 源信號數m和觀測信號數n之間存在關系m≤n。

3)si(i=1,2,…,m)中只允許一個源信號滿足高斯分布。

4) 對各源信號的概率分布略有些先驗知識。例如,某些音樂信號具有超高斯(super-Gassian)特性(如拉普拉斯分布)。

用向量wi表示第i次投影時的投影向量,則信號分離模型為

(2)

式(2)中zi(t)是提取的第i個分離信號。投影向量wi需要選擇使投影后數據間獨立性最大的向量。并由大數定理可知,幾個相互獨立的隨機變量之和也趨近于高斯分布。因此,提取的信號非高斯性達到最大時,信號間的獨立性也最大。信號的非高斯性可用負熵來衡量,定義為任意概率密度函數和具有相同方差的高斯密度函數間的K-L散度:

=Hg(z)-H(y)≥0

(3)

根據非高斯最大化準則,將概率密度函數p(z)展開為

(4)

式(4)中:pg(z)是具有相同方差的高斯分布;F(i)(z)是滿足如下條件的函數:

(5)

(6)

一般取N等于1和2,即取函數F(1)(z)和F(2)(z),F(1)(z)用來表示對稱性,概率密度函數的非對稱性,F(2)(z)用來表示在原點左右的雙峰性。此時,負熵可按下式進行計算:

J(z)≈w1{E[F(1)(z)]}2+w2{E[F(2)(z)]

-E[F(2)(v)]}2

(7)

式(7)中:v與y具有相同方差的零均值高斯隨機變量。當概率密度對稱時可化簡J(z)為

J(z)=E[F(2)(z)]-E[F(2)(v)]

(8)

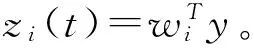
J(z)=E[F(2)(z)]-E[F(2)(v)]+β/2(‖wi‖2-1)

(9)

對wi求導,有

(10)

函數f(z)是F(2)(z)的導數。當進入穩態時,式(10)所示導數為零,即

γE[tf(wiTt)]+βwi=0

(11)

對式(11)進行牛頓迭代法求解,迭代公式為

(12)

t是球化后的數據,近似有

E[ttTf′(wiT(k)t)]≈E[f′(wiT(k)t)]

(13)

將式(13)代入式(12)并化簡可得快速獨立分量分析算法:

(14)

當對多個源信號進行提取時,一般只需選取不同wi(0),進行迭代即可,但為了保證每次提取的都是尚未提取過的源信號,需要在迭代前進行正交化,目的是把已提取分量去掉。

綜上所述:基于負熵的快速獨立分量分析算法步驟為

1) 解球化矩陣W;

2) 任取wi(0),規定‖wi(0)‖=1;

3) 迭代,wi(k+1)=E[tf(wiT(k)t)]-E[f′(wiT(k)t)];

4) 正交化,并且歸一化wi(k+1)=wi(k+1)/‖wi(k+1)‖;

5) 若wi不收斂,跳轉步驟3),直至求解完成。

4 仿真結果分析

實驗中包含了四組含噪信號,采樣點數均設定為800點,將小波濾波后與FastICA算法用于盲信號分離有下圖2為四組原始信號。假定矩陣A為方陣,在Matlab中矩陣A線性混合這四組即將分離的信號,查詢得A為如下矩陣:

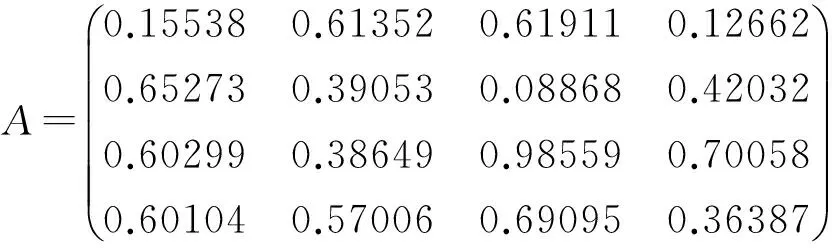
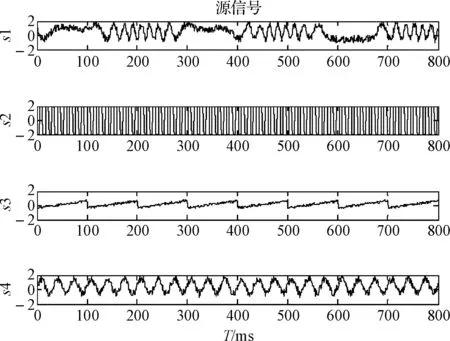
圖2 四組原始信號

圖3 觀察的混合信號

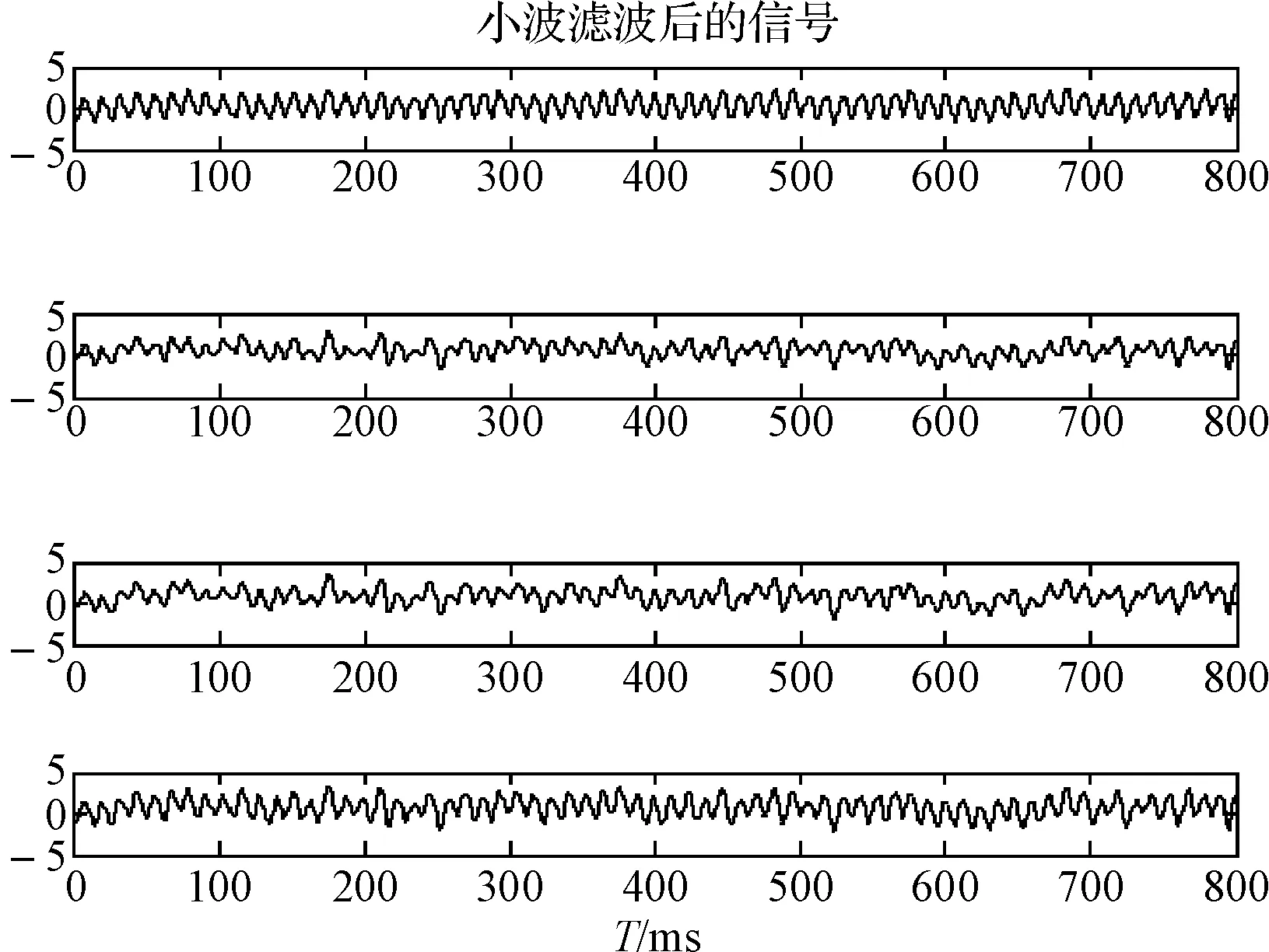
圖4 小波濾波后的混合信號

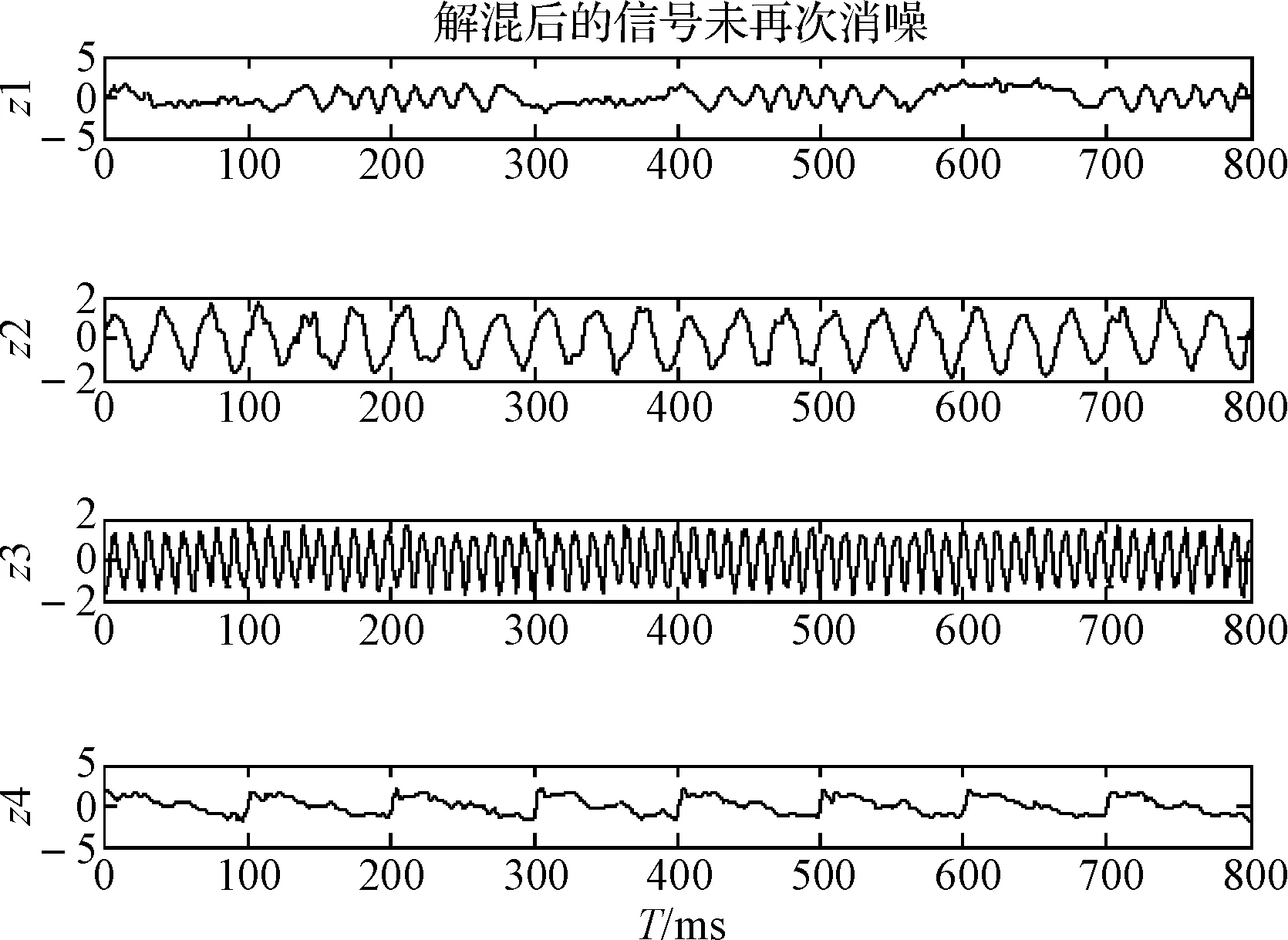
圖5 分離后未再次去噪的信號

圖6 分離后再次小波去噪

由圖3和圖4可以得出圖4中經過小波濾波后的信號明顯變得比圖3中的信號噪聲降低很多,由圖2(s1、s2、s3、s4)為原始信號和圖5(z1、z2、z3、z4)為分離出來的信號,其中原始信號s1、s2、s3、s4分別對應于分離后的信號z1、z3、z4、z2,信號的順序作了一定調整,信號的大小和幅度也作了相應調整,但不礙于信號識別。

可以求得相似矩陣G相似矩陣G理想情況應為單位矩陣,可以看出G矩陣每行每列都有一個元素1,其余位置上的元素很小,可以近似看作0,并且可以得知矩陣存在一定誤差,這也說明了原始信號s1、s2、s3、s4與分離信號z1、z2、z3、z4的對應關系和它們之間存在的誤差。總的來說,可以得出應用小波濾波和FastICA算法分離得到的信號與原始信號相似度很高,可以得出結果。

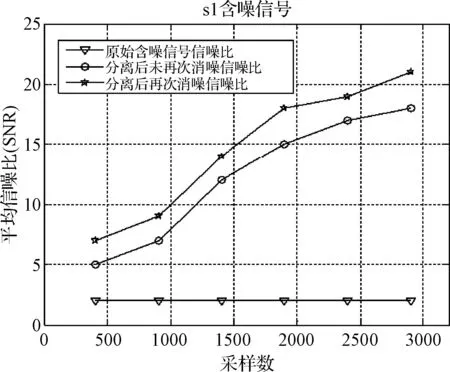
圖7 s1信號采樣點數與平均信噪比

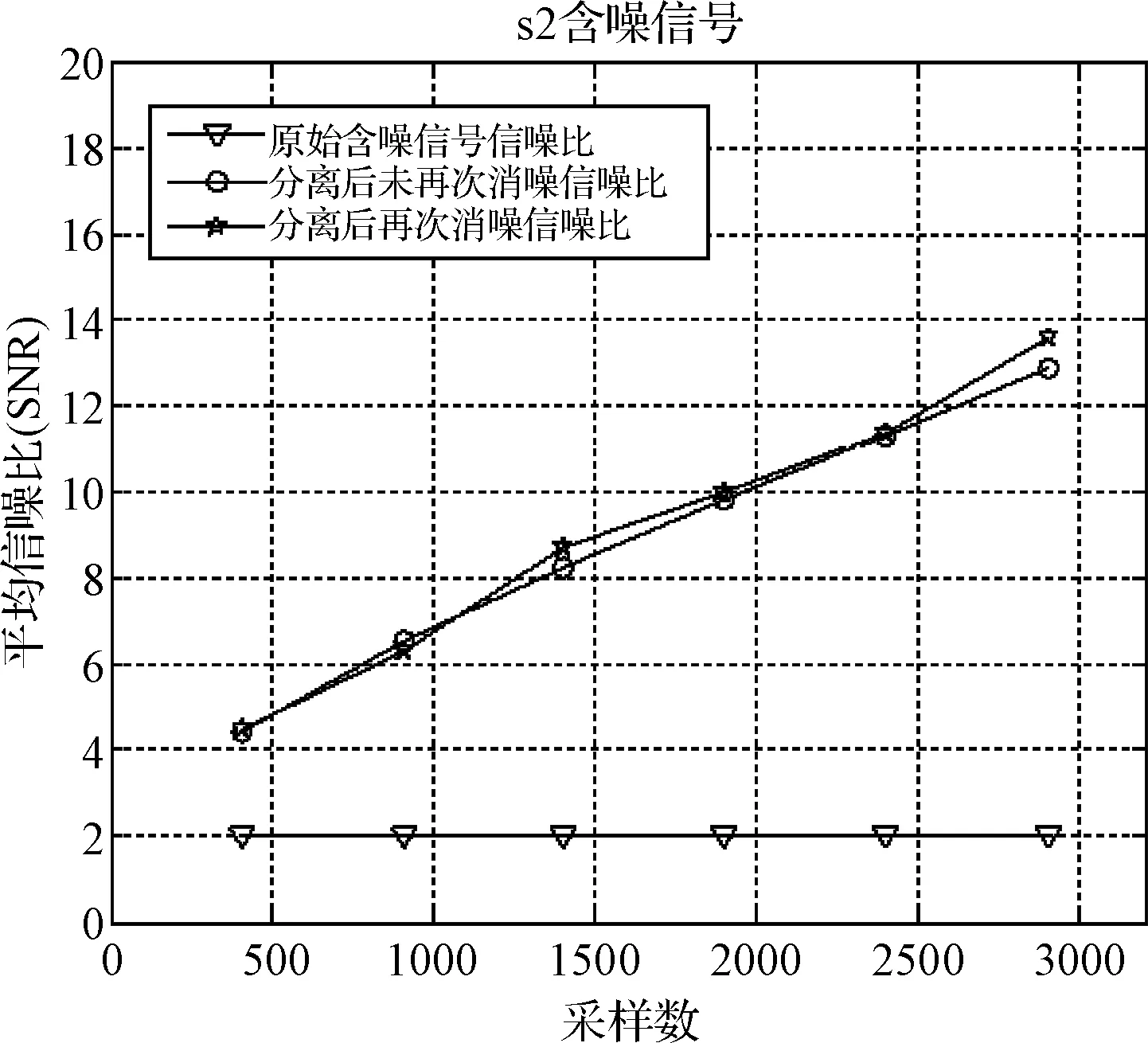
圖8 s2信號采樣點數與平均信噪比

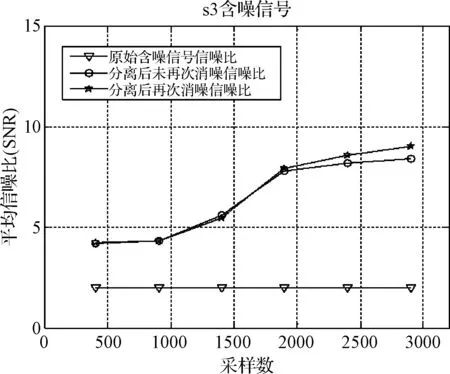
圖9 s3信號采樣點數與平均信噪比

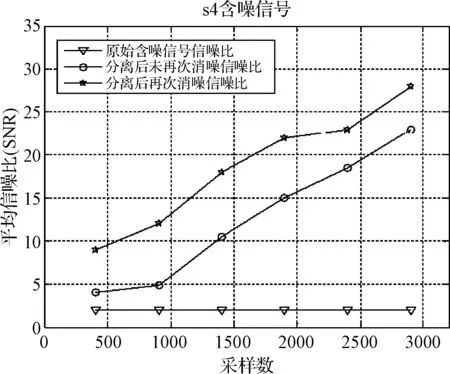
圖10 s4信號采樣點數與平均信噪比

進行500次實驗,通過分析各含噪信號不同階段的平均信噪比來量化該系統的性能。可以分別得到四個原始含噪信號信噪比、分離后未再次去噪信噪比和分離后再次去噪信噪比曲線圖。對比可以得出:經過一次去噪處理和二次去噪處理的信號信噪比明顯比原始含噪信號信噪比大幾至幾十dB,但二次去噪處理性能優劣程度與原始信號形式有一定關系,并且隨著采樣點數增加進行去噪處理后的信號信噪比有逐漸增大的趨勢。

5 結語

本文介紹了基于小波濾波的自適應快速獨立分量分析算法過程,并且應用于四個獨立信號的盲分離,先通過小波濾波使混合信號盡可能平滑,然后通過FastICA算法分離濾波后的混合信號,再次使用小波濾波,通過從分離前后的波形比較及平均信噪比的比較,說明基于二次小波濾波的自適應快速獨立分量分析算法是一種較好的信號分離方法,可以在語音盲信號分離中進行推廣,具有一定的發展潛力。

[1] 史習智.盲信號處理—理論與實踐[M].上海:上海交通大學出版社,2008:1-85.

[2] 劉琚,孫建德,許宏吉.盲信號處理理論與應用[M].北京:科學出版社,2013:117-119.

[3] 韋力強.基于小波變換的信號去噪研究[D].長沙:湖南大學,2007:14-15.

[4] 馬曉紅,殷福亮,陸曉燕,等.基于小波變換的傳聲器陣列語音增強方法[J].大連理工大學學報,2003,43(4):511-515.

[5] Hyvarinen A, Karhunen J, Oja E. Independent Component Analysis[M]. New York: Wiley,2001:147-161,293-304,391-406.

[6] 彭玉華.小波變換與工程應用[M].北京:科學出版社,1999:59-62.

[7] Potamitis I, Fakotakis N, Kokkinakis G. Speech enhancement using the sparse code shrinkage technique[C]//Proceedings of the IEEE International Conference on Acoustic, Speech and Signal Processing,2001:621-624.

[8] Cardoso J F, Souloumiac A. Blind beamforming for non-Gaussian signals[J]. IEEE Proceeding-F,1993,140(6):362-370.

[9] Kotani M, Shirata Y, Maekawa S, et al. Application of independent component analysis to feature extraction of speech[C]//Proceeding of the IEEE International Joint Conference on Neural Networks,1999:2981-2984.

[10] 孫守宇.盲信號處理基礎及應用[M].北京:國防工業出版社,2010.

[11] 萬堅,涂世龍,廖燦輝,等.通信混合信號盲分離理論與技術[M].北京:國防工業出版社,2012.

[12] 余先川,胡丹.盲源分離理論與應用[M].北京:科學出版社,2011.

[13] 李正周.Matlab數字信號處理與應用[M].北京:清華大學出版社,2008.

[14] 陳懷琛.數字信號處理教程—Matlab釋義與實現[M].北京:電子工業出版社,2004.

[15] 薛年喜.Matlab在數字信號處理中的應用[M].第2版.北京:清華大學出版社,2008.

FastICA Blind Source Separation Based on Secondary-wavelet Denoising

ZHAO Kui HUANG Gaoming

(School of Electronic Engineering, Naval University of Engineering, Wuhan 430033)

A three-step method about noise mixed signal separation is put forward in this paper, the wavelet filter de-noising processing method and the fast independent component analysis(FastICA) blind sources separation technique to are used realize the separation, then the wavelet filtering method is used again to the separated signals. The simulation results show that the technique performs well in signal separation by comparing the waves and signal to noise ratio before and after separation and it has good denoising performance and separation effect.

wavelet filter, independent component analysis, waveform, average signal noise ratio

2014年12月5日,

2015年1月26日

趙奎,男,碩士研究生,研究方向:信號與信息處理。黃高明,男,教授,博士生導師,研究方向:盲信號處理。

TN911

10.3969/j.issn1672-9730.2015.06.011