基于最小二乘算法的OFDM信道估計*

黃 波 王 琦 徐強輝

(中國船舶重工集團公司第七二二研究所 武漢 430250)

?

基于最小二乘算法的OFDM信道估計*

黃 波 王 琦 徐強輝

(中國船舶重工集團公司第七二二研究所 武漢 430250)

作為一種高效的傳輸技術,正交頻分復用(OFDM)正被廣泛地應用于下一代無線通信系統。論文采用一種OFDM系統中低復雜度的最小二乘(LS)信道估計算法,該算法采用在頻域上插人梳狀導頻數據,通過仿真,證明了該算法在瑞利衰落多徑信道中的優越性。同時,仿真也表明,當信道變化過快時,該算法的優越性將變得不再顯著。

正交頻分復用技術; 最小二乘; 信道估計

Class Number TN929.531

1 引言

正交頻分復用技術(Orthogonal Frequency Division Multiplexing,OFDM)是多載波調制(Multi-Carrier Modulation,MCM)的一種。其主要思想是:將信道分成若干正交子信道,將高速數據信號轉換成并行的低速子數據流,調制到在每個子信道上進行傳輸[1]。正交信號可以通過在接收端采用相關技術來分開,這樣可以減少子信道之間的相互干擾ICI。每個子信道上的信號帶寬小于信道的相關帶寬,因此每個子信道上的可以看成平坦性衰落,從而可以消除符號間干擾。而且由于每個子信道的帶寬僅僅是原信道帶寬的一小部分,信道均衡變得相對容易。在向B3G/4G演進的過程中,OFDM是關鍵的技術之一,可以結合分集、時空編碼、干擾和信道間干擾抑制以及智能天線技術,最大限度地提高了系統性能[2]。包括以下類型:V-OFDM,W-OFDM,F-OFDM,MIMO-OFDM,多帶-OFDM。

由于接收端的相干解調需要信道估計,因此信道估計是OFDM系統的關鍵技術之一,信道估計的方法主要分為三類:基于導頻的估計、盲估計和半盲估計[3]。考慮算法的復雜度,實際的OFDM系統中通常采用的信道估計方法都是基于導頻的確知性估計算法,即在發射數據流中插入導頻信號,接收端提取導頻從而得到導頻上的信道響應,再利用插值的方法估計其它數據載波位置上的信道響應。

本文采用多徑衰落的信道模型,主要研究了基于頻域插入梳狀導頻的最小二乘(LS)信道估計算法[4～6],并且分析比較了在不同多徑數的情況下LS信道估計與沒有信道估計的結果。

2 OFDM系統結構

以OFDM方式實現的多載波調制如圖1所示。輸入數據經過QAM調制得到一個復數的數據序列X[0],X[1],…,X[N-1]。經過串并變換后的N個并行QAM符號X[0],X[1],…,X[N-1]對應N個子載波上傳輸的符號,也就是OFDM調制器輸出信號s(t)的離散頻率分量。這N個頻率分量經過逆DFT變換后成為s(t)的時域抽樣值,逆DFT可利用IFFT高效實現。IFFT所產生OFDM符號由長度為N的序列x[n]=x[0],x[1],…,x[N-1]組成,其中

(1)

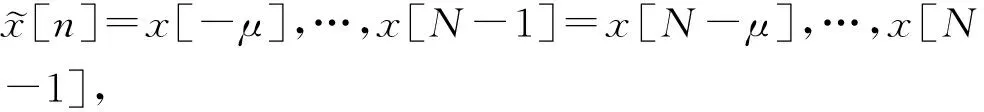
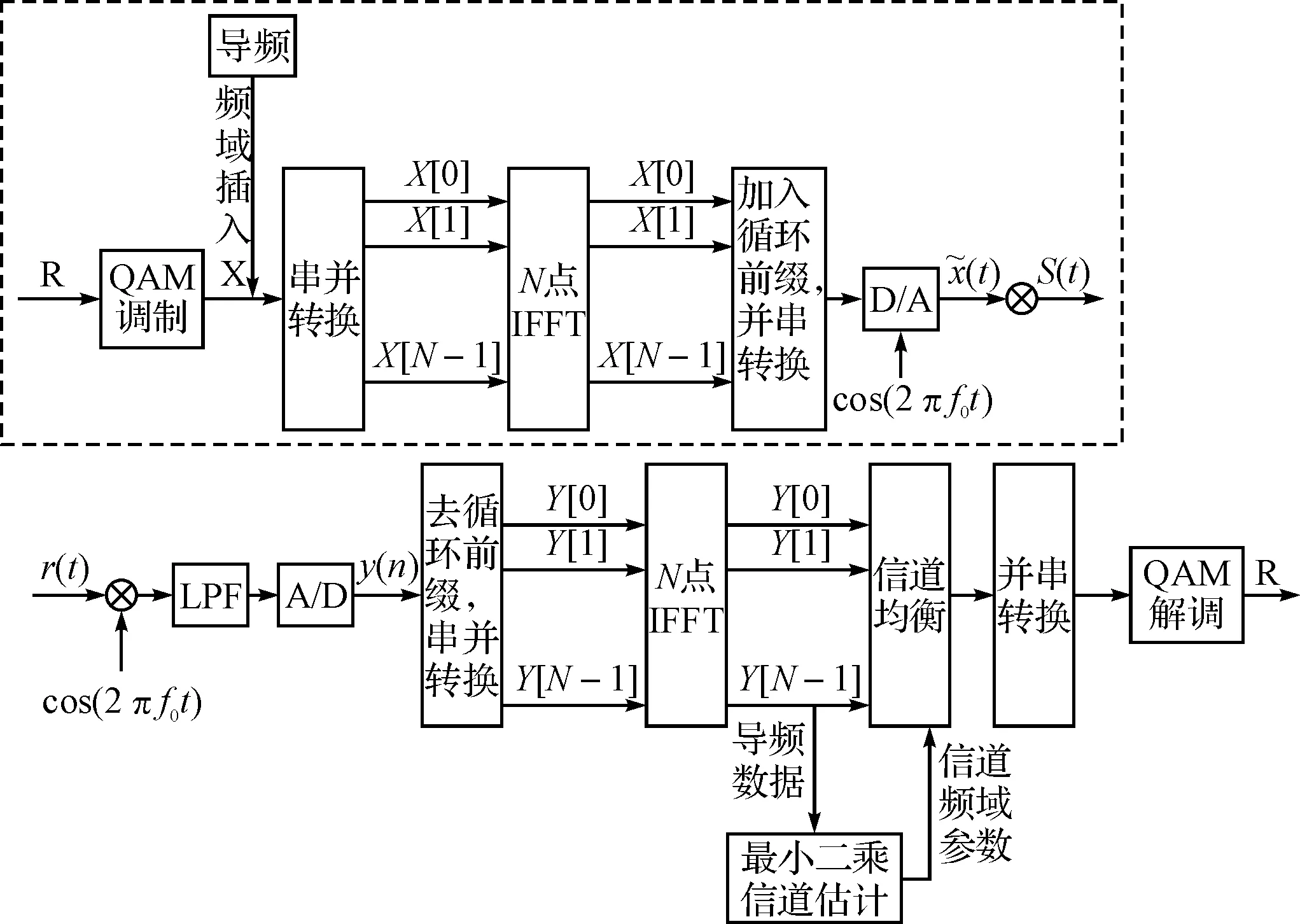
圖1 OFDM系統框圖

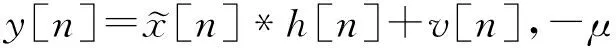
OFDM系統將帶寬信道分解為相互正交的一組窄帶子信道,每個子信道上傳輸不同的QAM符號。這種分解不需要已知信道增益H[i],i=0,…,N-1,如同把頻率響應為H(f)的連續時間信道分割為正交信道時也不需要知道H(f),只要把發送信號的頻譜分割為不相重疊的子帶。解調器將Y[i]除以信道增益H[i]就可以復原QAM符號,這個過程也叫頻域均衡。

3 基于頻域插入導頻的OFDM信道估計

在OFDM系統中,頻域的信道估計算法,大都是基于導頻的信道估計算法[7～8]。導頻插入方式不同,其應用環境就不同,傳輸業務也存在一定的差異。目前,主要有兩類導頻插入方式:一是根據抽樣定理,在時頻二維空間上插入梳狀導頻,即按照一定規律將導頻分布在整個時頻空間上;二是訓練符號的方式,即在某些符號的所有子載波上都插入導頻,而在隨后的一些符號中插入極少的導頻甚至不插入導頻[9]。采用訓練符號的導頻插入方式,往往只是在開始發送一些訓練符號,這就要求信道在相當長的時間內變化較小,甚至不變,即所謂準靜止信道、慢衰落信道。由此可見,這種方法較適用于恒參信道、WLAN信道等。同時,由于在訓練符號內所有子載波都用來發送導頻符號,所以可選用低階的信道估計算法。如果信道中有較大的多普勒頻移[10],信道變化較快,則不能選用插入訓練符號的導頻插入方式,而應在整個信號的時頻空間內插入梳狀導頻信號。這種情況下,還應考慮所插入導頻的數量問題。從可靠性角度考慮,插入的導頻符號越多,估計就越準確,極端情況就是只發送導頻符號;但若從傳輸有效性角度來考慮,插入的導頻越多,有效數據的傳輸速率就越低,且在發送能量一定的條件下降低了有效信噪比,所以應插入盡可能少的導頻信號[11]。因此,實際系統中應在準確度和傳輸有效性之間取得折衷,根據具體情況選擇恰當的導頻插入方式。

本文考慮的是無線多徑衰落信道[12],信道的變化較快,因此選取的是基于頻域插入梳狀導頻的信道估計方法。

如圖1虛線部分所示,信源發出的二進制信息經過信道編碼和交織以后成組地映射成QPSK或QAM信號,插入頻域導頻數據塊之后,頻域有效數據和導頻一起經過IFFT變換成為時域數據和時域導頻,然后加上循環前綴CP,經過D/A發送出去。接著發送信號通過頻率選擇性多徑衰落信道,接收信號經過A/D和去CP,再進行FFT變換,得到:

Y=XH+W

(2)

式(2)中H是頻域信道矩陣,X是頻域發射信號矩陣,Y為頻域接收信號矩陣,W為加性白高斯噪聲矩陣。若要將信號恢復出來,必須得到準確的H的信息,即進行信道估計。基于頻域的信道最小二乘估計為

(3)

4 系統參數

本文選取的信道模型是帶多普勒頻移的瑞利衰落無線多徑信道,采用頻域插入梳狀導頻的方式,利用LS算法來進行信道估計,其中系統參數設置如表1所示。

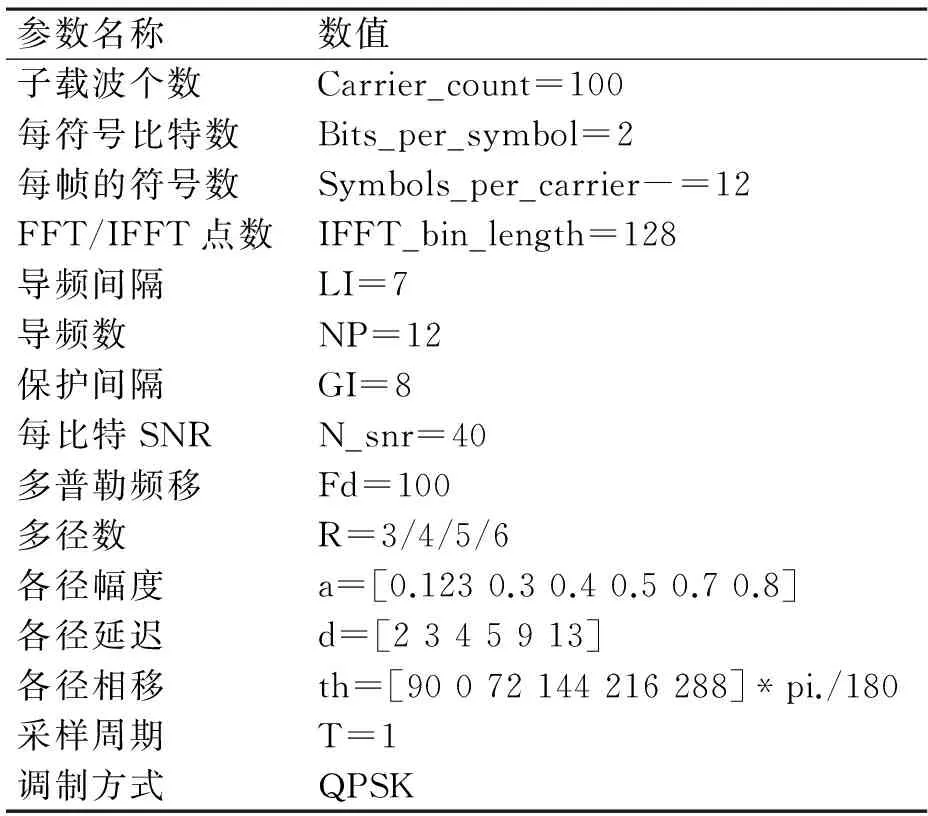
表1 系統參數表

5 仿真結果

本文的仿真結果如圖2所示,由圖2(a)可以看出,利用LS方法進行信道估計的系統誤碼率比沒有信道估計的系統誤碼率有明顯的減小。比較圖2中的(a)、(b)、(c)可以發現,隨著多徑數量的增加,不管有無信道估計,系統的誤碼率都明顯增加,并且隨著多徑數量的增加,LS信道估計相對于無信道估計的方法所獲得的系統誤碼率的減少逐漸變得不明顯,圖2(a)中,當多徑數為3時,LS相比無信道估計的方法獲得的誤碼率的提升達到兩個數量級;圖2(b)中,當多徑數為4時,LS相比無信道估計的方法獲得的誤碼率的提升只有一個數量級;圖2(c)中,當多徑數為5時,LS相比無信道估計的方法獲得的誤碼率的提升甚至不到一個數量級。觀察圖2(d)可以發現,當多徑數為6時,LS信道估計的性能甚至比無信道估計的系統性能更差。

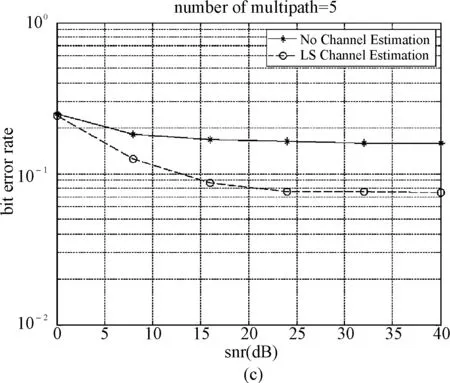
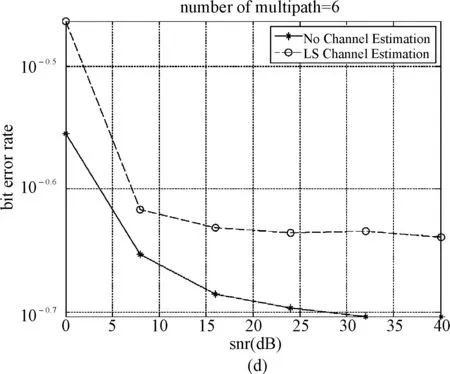
圖2 LS信道估計與無信道估計的誤碼率比較

6 結語

本文研究了OFDM系統中利用LS方法進行信道估計的技術,通過仿真得出,當多徑數在一定范圍內時,LS信道估計的方法比無信道估計的方法的誤碼率低,隨著多徑數目的增加,LS方法的優勢逐漸減弱,而當多徑數達到一定程度時,LS方法的性能甚至變得比無信道估計要差,說明此時的信道變化太快,按照原有的方式已經難以進行信道估計了。

[1] Linglong Dai, Zhaocheng Wang, Zhixing Yang. Time-Frequency Training OFDM with High Spectral Efficiency and Reliable Performance in High Speed Environments[J]. IEEE Journal on Selected Areas in Communications,2012(30):695-707.

[2] Changyong Shin, Heath R. W., Powers E. J. Blind Channel Estimation for MIMO-OFDM Systems[J]. IEEE Transactions on Vehicular Technology,2007(56):670-685.

[3] 張繼東,鄭寶玉.基于導頻的OFDM信道估計及其研究進展[J].通信學報.2003,24(11):116-124.

[4] Muck M., de Courville M., Duhamel P. A pseudorandom postfix OFDM modulator-semi-blind channel estimation and equalization[J]. IEEE Transactions on Signal Processing,2006(54):1005-1017.

[5] Tomasin, S., Butussi, M. Analysis of interpolated channel estimation for mobile OFDM systems[J]. IEEE Transactions on Communications,2010(58):1578-1588.

[6] 鄭濟均,林競力,朱維樂.基于T-MMB標準的OFDM信道均衡技術[J].電子科技大學學報,2011,40(5):682-685.

[7] 姜俊迪,林如儈.一種OFDM時域導頻插入的最小二乘估計方法[J].電子測量技術,2008,31(1):34-37.

[8] Die Hu, Xiaodong Wang, Lianghua He. A New Sparse Channel Estimation and Tracking Method for Time-Varying OFDM Systems[J]. IEEE Transactions on Vehicular Technology,2013(62):4648-4653.

[9] 劉偉鋒,樊濱溫.基于小波去噪的OFDM信道估計技術研究[J].計算機仿真,2013,30(8):185-189.

[10] 黃敏,李兵兵.基于整體最小二乘的聯合信道估計及OFDM信號檢測算法[J].電子與信息學報,2014(6):1448-1453.

[11] 解永生,汪明亮,周磊磊.線性時變信道下OFDM系統的加窗信道估計[J].華南理工大學學報(自然科學版),2013,41(5):43-47.

[12] Ming Liu, Crussiere, M., Helard, J. A Novel Data-Aided Channel Estimation With Reduced Complexity for TDS-OFDM Systems[J]. IEEE Transactions on Broadcasting,2012(58):247-260.

OFDM Channel Estimate Based on Least Square Algorithm

HUANG Bo WANG Qi XU Qianghui

(No. 722 Research Institute of CSIC, Wuhan 430250)

OFDM(Orthogonal Frequency Division Multiplexing) is being widely used in the next generation of wireless communication systems as an efficient transmission technology. In this paper, a low complexity LS(least squares) channel estimation algorithm which inserting comb pilot data in the frequency domain is proposed in OFDM system. Simulation results prove the superiority of the algorithm in Rayleigh multipath fading channel. Meanwhile, the simulation results also show that the superiority of this algorithm will become no longer significant when the channel changes too fast.

OFDM, least square, channel estimate

2014年12月7日,

2015年1月25日

黃波,男,工程師,研究方向:無線通信。王琦,男,碩士,工程師,研究方向:艦船通信系統。徐強輝,男,工程師,研究方向:無線通信。

TN929.531

10.3969/j.issn1672-9730.2015.06.015