基于PEEC理論的線纜建模方法*

周 磊 孫艷超 林 健 劉 振

(1.海裝合同監督管理部 北京 100841)(2.中船重工第七二二研究所 武漢 430205)

?

基于PEEC理論的線纜建模方法*

周 磊1孫艷超2林 健2劉 振2

(1.海裝合同監督管理部 北京 100841)(2.中船重工第七二二研究所 武漢 430205)

隨著艦船上設備的增多,用于設備間通信的連接線纜的相互耦合越來越不可忽視。部分元等效電路方法(PEEC)作為一種場路結合的方法,通過場的方法提取等效電路參數,形成等效電路模型,進而進行相應的電路仿真計算。將PEEC方法應用于線纜建模,可以準確而高效地提取其等效電路模型,完成線纜的仿真計算。文章簡述了PEEC方法的基本原理,并針對線纜的結構特點,對基本PEEC方法進行了相應的改進使其更加適用于線纜的等效電路建模。

部分元等效電路方法; 簡單線纜結構; 等效電路模型; 等效電位系數

Class Number TP391

1 引言

部分元等效電路方法的提出最初是為了解決實際應用中的電磁兼容問題、互連問題和封裝問題。它是一種能夠解決電路和電場混合問題的全波算法,可以同時應用于時域和頻域。文獻[1～3,7～8]中應用PEEC方法解決了各種問題,證明此方法的廣泛性和靈活性。

隨著艦船上設備的增多,用于設備間通信的連接線纜的相互耦合越來越不可忽視。然而由于線纜的長度相對于截面尺寸過大,使得完全基于場理論的方法(如FDTD、MoM等)計算線纜間串擾耦合的效率不高。PEEC是一種場路結合的方法,通過場的方法提取等效電路參數,形成等效電路,進而用路的方法進行相應的仿真計算,因而將其應用于線纜可以準確而高效地計算出線纜上的傳導信號及線纜間的串擾耦合。

在應用PEEC方法對電磁兼容問題進行建模和求解時,對物體進行網格剖分是首要也是關鍵的一步,這很大程度決定了所建模型的精確度。對線纜進行建模時,由于線纜的截面尺寸小于剖分單元尺寸,只需沿著線纜長度方向進行一維剖分,因此使用基本PEEC方法效率并不高。本文針對簡單線纜結構提出一種新方法來計算部分電位系數。這種方法能夠很大程度上提高建模效率減少求解時間,同時不降低原有PEEC方法的精度。

2 基本PEEC方法理論

將磁矢量表達式和電位表達式代入電場積分方程,可得下式[9]:

(1)

=Plm(ω)Qm(ω) forl=1,…,Ns

(2)

因此,Ns個面單元的電位與其電荷的關系可以用下式表示(在頻率點ω):

Φ(ω)=P(ω)Q(ω)

(3)

式(2)應用伽略金法則后,可以寫成:

(4)

每一項都代表了體單元Vi上的壓降,上式可以寫為

(5)

其中:

(6)

Lp,in為體單元i和n之間的部分電感。

式(5)用矩陣形式可以表示為

-AΦ(ω)-RIL(ω)-jωLP(ω)IL(ω)-V0(ω)=0

(7)

其中Φ(ω)表示定點到無窮遠處的電位值,IL(ω)為支路電流,矩陣A為連接矩陣[2]。電路方程(3)和(7)分別表示電場耦合和磁場耦合,由此可以得到部分元等效電路。

3 一種高效的等效電位系數計算方法

網格剖分對于有效精確的PEEC建模來說是關鍵的一步,因為它決定了電路網絡的復雜度。未知數的數量,這些直接影響所建等效電路模型的求解時間。PEEC方法中,導體內部的剖分體單元為長方體,導體表面的剖分面單元為長方形,單元的尺寸由最大頻率決定。通常為了保證PEEC模型的穩定性,規定最大剖分尺寸為最小波長的1/20[10]。

剖分網格中的節點為等效電路中的節點。為了減少總的節點數量,建立高效的PEEC模型,剖分時要保證不同方向的節點共用。為此,剖分時采用邊緣體單元尺寸為內部體單元一半的方法,并保證導體外表面的面單元與體單元相差半個單元尺寸。圖1顯示了體單元剖分、面單元剖分和節點的放置。

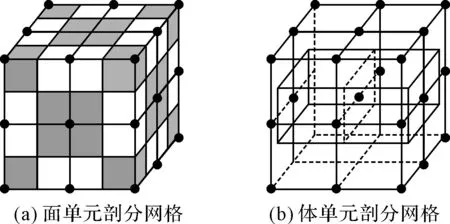
圖1 簡單結構導體剖分

本文主要研究基于PEEC方法對簡單線纜結構進行建模求解,進而得到線纜上的信號值或線纜間的串擾值。以簡單的微帶線模型為例,由于截面尺寸小于剖分單元尺寸,只需沿其長度方向進行一維網格剖分即可,如圖2所示。

注:實線為電感分割線,虛線為電容分割線
圖2 微帶線的網格剖分

取一個中間的體單元為例,如圖3(a)所示,其包括四個節點。根據基本PEEC方法,要使容性支路和感性支路兼容,需要將其剖分成四個體單元,由此得到四個感性支路,如圖3(b)所示。可見,這種剖分方式得到的等效電路較復雜,求解時間也會相對較長。為了改進基本PEEC方法,使之能夠有效地對線纜結構建模,引入等效電位系數的概念。基于計算等效電位系數,可得到改進后的單元等效電路如圖3(c)所示,所建PEEC模型得到了很大程度的簡化。

(a)示例體單元

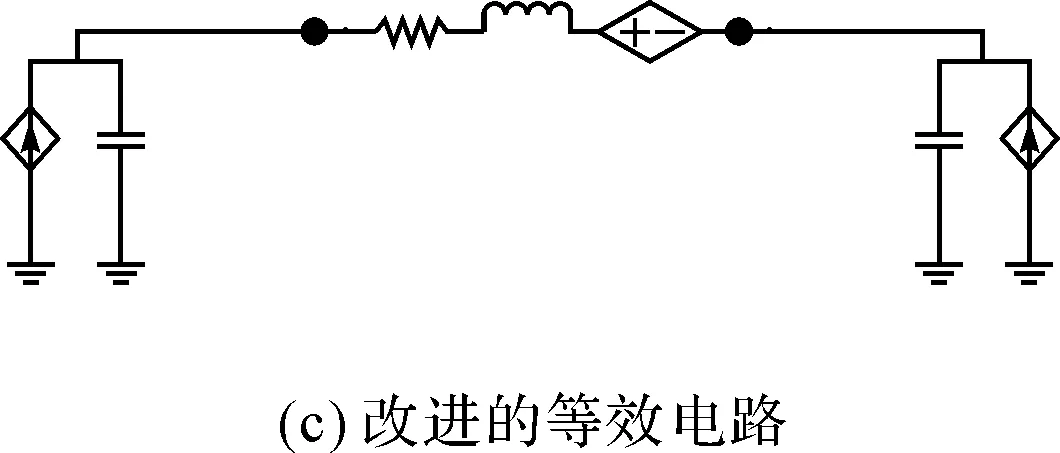
圖3 體單元的不同等效電路

等效電位系數方法是通過將體單元的四個面考慮為一個整體,計算整體的電位系數實現的。體單元的四個面的電位相等,而其電荷為每個面的電荷之和,關系如下式:

Φeq=Φ1=Φ2=Φ3=Φ4

(8)

Qeq=Q1+Q2+Q3+Q4

(9)

其中Φ1,Φ2,Φ3,Φ4分別代表體單元四個不同面的電位;Q1,Q2,Q3,Q4分別代表體單元四個不同面的電荷,Φeq、Qeq分別為等效單元的電位和電荷。

根據電位與電荷的關系,對于任意體單元有式(10)的關系:

Φ=PQ

(10)

其中P為電位系數矩陣。

等效電位系數的計算可以通過引入降階矩陣R來實現。定義RV為電位矩陣的降階矩陣;定義RQ為電荷矩陣的降階矩陣,且存在關系式:

(11)

設降階前的電位矩陣為Φ;降階前的電荷矩陣為Q;降階后的等效單元的電位矩陣為Φeq,降階后的等效單元的電荷矩陣為Qeq。

可得到下列等式:

Φeq=RVΦ

(12)

Q=RQQeq

(13)

根據電位與電荷的關系(式(10)),推導式(12)、式(13)可得:

(14)

進而可得等效電位系數矩陣的關系式:

(15)

其中Peq表示等效電位體單元的等效電位系數矩陣。

4 簡單應用實例

下面以簡單的平行帶狀線纜結構為例,如圖4所示,使用基于等效電位系數的PEEC方法對其進行建模并使用改進結點法求解其線端的信號值,通過將求解結果與CST軟件的仿真結果對比,驗證所提方法的正確性及高效性。

圖4 簡單的帶狀線纜結構示意圖

當設置所加電流源為1A時,可得到PEEC等效模型的求解結果如圖5所示,CST仿真結果如圖6所示。

圖5 平行雙線的PEEC求解結果

圖6 平行雙線的CST仿真結果

由于CST仿真需設置參考地面,所以與PEEC模型求解結果有微小偏差。由圖5、圖6任取相同橫坐標的兩點,比較其縱坐標的結構,可知結果誤差小于1%,可驗證所建PEEC模型的正確性。使用PEEC方法對線纜進行建模及分析與CST相比,整個分析過程所需時間僅為CST的20%左右,對于計算機內存的需求也遠小于CST,所以PEEC方法對于線纜建模并求解傳導信號或線纜之間的串擾值是有絕對優勢的。

5 結語

本文通過提出等效電位系數的概念,改進了基于基本PEEC理論的線纜建模方法,使PEEC建模效率顯著提高,同時在不降低精度的情況下簡化了等效電路模型,進而節約了求解資源及求解時間。文章最后通過簡單帶狀線的例子證明了所提出方法的正確性。

[1] A. E. Ruehli. Equivalent Circuit Models for Three Dimensional Multi-conductor Systems[J]. IEEE Transactions on Microwave Theory and Techniques,1974,22(3):216-221.

[2] G. Antonini. The partial element equivalent circuit method for EMI, EMC and SI analysis[J]. ACES Newsletter,2006,21(1):8-32.

[3] H. Heeb, A. Ruehli. Three-Dimensional Interconnect Analysis Using Partial Element Equivalent Circuits[J]. IEEE Transactions on Circuits and Systems,1992,38(11):974-981.

[4] G. Antonini, A. Orlandi, A. Ruehli. Analytical Integration of Quasi-Static Potential Integrals on Non-Orthogonal Coplanar Quadrilaterals for the PEEC Method[J]. IEEE Transactions on Electromagnetic Compatibility,2002,44:399-403.

[5] V. Akcelik, B. Jaramaz, O. Ghattas. Nearly orthogonal two-dimensional grid generation with aspect ratio control[J]. Journal of Computational Phyics,2001,171:805-821.

[6] Song, Z., D. Su, F. Duval, et al. Model order reduction for PEEC modeling based on moment matching[J]. Progress In Electromagnetics Research,2011,114:285-299.

[7] Z. F. Song, F. Dai, D. L. Su, et al. Reduced PEEC Modeling of Wire-ground Sructures Using a Selective Mesh Approach[J]. Progress In Electromagnetics Research,2012,123:355-370.

[8] L. K. Yeung, K.-L. Wu. Generalized partial element equivalent circuit(PEEC) modeling with radiation effect[J]. IEEE Trans. Microwave Theory Tech.,2011,59:2377-2384.

[9] A. Alparslan, M. Aksun, K. Michalski. Closed-form Green’s functions in planar layered media for all ranges and materials[J]. IEEE Trans. Microwave Theory Tech.,2010,58:602-613.

[10] Wang S, He J, Zhang B, et al. A Time-Domain Multiport Model of Thin-Wire System for Lightning Transient Simulation[J]. IEEE Transactions on Electromagnetic Compatibility,2010,52(1):128-135.

A Method for Cable Modeling Method Based on PEEC

ZHOU Lei1SUN Yanchao2LIN Jian2LIU Zhen2

(1. Contract Supervision and Management Department of PLAN Equipment Department, Beijing 100841) (2. No. 722 Research Institute of CSIC, Wuhan 430205)

With the increase of equipment on ships, the electromagnetic coupling between cables which used for communication among devices cannot be ignored. PEEC is a complex method of field and circuit. In PEEC, parameters are extracted from the analysis of field to obtain equivalent circuit. By simulating the circuit, signal of cables can be calculated accurately and efficiently. In this paper, the basic principle of PEEC is introduced, and in order to improve the calculation efficiency and accuracy in PEEC model for cables, some improvements are made in PEEC method based on the structural characteristics of cables.

PEEC method, simple cable structures, equivalent circuit model, equivalent capacitance

2014年12月14日,

2015年1月29日

周磊,男,工程師,研究方向:裝備采購管理、艦船總體、通信。孫艷超,女,助理工程師,研究方向:艦船通信系統設計。林健,男,助理工程師,研究方向:艦船通信系統設計。

TP391

10.3969/j.issn1672-9730.2015.06.022