基于管制員工作負荷的扇區容量評估方法研究*

任 民 閃 樂

(1.海軍指揮學院二系 南京 210016)(2.南京航空航天大學民航學院 南京 210016)

?

基于管制員工作負荷的扇區容量評估方法研究*

任 民1閃 樂2

(1.海軍指揮學院二系 南京 210016)(2.南京航空航天大學民航學院 南京 210016)

為準確評估某一空域容量,論文提出一種基于人類動力學測定管制員工作負荷的方法,該方法通過對管制員通信工作負荷特性進行分析,確定管制員工作過程屬于典型人類動力學,符合冪律分布。在此基礎上,利用多元線性回歸基本模型建立了基于管制員工作負荷的扇區容量評估模型。最后通過案例分析驗證了扇區容量評估模型的準確性。

空中交通管理; 容量評估; 人類動力學

Class Number V355.1

1 引言

終端空域的空中交通管制服務是由管制員來實施進行的,準確地評估管制員工作負荷是確定空域容量的基礎[1]。目前在該領域主要針對以下三個方面進行管制員工作負荷研究:第一是通過對管制員的生理狀態指標和行為種類數目的監測。由于難以確定眾多生理和行為指標的重要程度、各指標之間的關聯性等,導致評估工作較難實現[2]。第二是通過觀察和問卷形式的主觀測評管制員工作負荷,但該方法存在難以度量主觀精神工作負荷的局限性[3]。第三是通過評估不同的空域復雜程度下的管制指揮,獲取管制員工作負荷的水平。該方法對不同空域下的交通特征進行研究,進而確定管制員的工作負荷水平[4]。

除上述三種管制工作負荷研究外,理解和掌握空中交通系統中管制行為的動力學規律,可為確定管制員工作負荷準確評估提供依據,也是實現空域容量預測的前提和基礎。本文結合現有人類動力學方面的研究成果,將其運用到管制員的工作負荷中,提出基于人類動力學的終端容量評估方法。

2 管制員通信工作負荷的人類動力學分析

冪律分布及各種包含冪律分布的擴展分布形式是人類動力學中普遍存在的分布形式[5]。數學上,隨機變量X的概率密度函數如果可用如下公式表示:

f(x)=Cx-α

(1)

則稱變量X服從冪律分布。式中α是一個常量,被稱為冪律分布的冪指數或標度參數,冪律分布是一類特殊的重尾分布形式,它具有多種多樣的表現形式并廣泛存在于眾多學科領域之中[5]。

經過研究表明[6],線性裝箱法需要大量數據支撐且要求的箱體寬度要很精確,而這在實際應用中很難實現(通常應用中設置的箱體寬度比較隨機),故其在求解過程中的不是最優的;對數裝箱法雖然解決了數據需求方面的問題,但仍然對箱體寬度的選擇有較高要求;累積分布函數擬合法對變量的累積分布函數進行分析,避免了選擇箱體的問題,但其仍不能直接求得α的值,而是通過求α+1得到α的值,其中難免會形成一定的誤差;而極大似然估計法則可避免上述問題,故本文采用極大似然估計法進行求解,具體過程如下。

對常數C做歸一化處理,歸一化方程為

(2)

若α>1,則上式可簡化為

(3)

則冪律分布方程為

(4)

給出由n個xi組成的集合{xi},則分布中xi出現的概率與下數成正比:

(5)

該數稱之為數據集的似然值。而真正想得到的是基于集合{xi}的α的概率值,由貝葉斯定律可知:

(6)

數據的先驗概率P(x)是固定的——在集合{xi}中為1,其他時候為0。通常認為,在沒有任何不滿足該條件的情況下,指數α的先驗概率P(α)是統一的,即一個常數。因此,P(α|x)∝P(x|α)。為方便起見,通常使用極大似然函數L的對數值logL來代替的P(α|x)對數值,它們在數值上是相等的,其中:

(7)

現在通過α的極大似然估計值來計算最可能的α值。由于L是個單調增的函數,令δL/δα=0,可得:

(8)

或者

(9)

定義1 管制事件為一段連續的包含一條或多條管制指令(包括給機長發布指令和聽機長復述指令)的語音通話。

其中,相鄰管制事件間的間隔時間X是本文主要研究對象。通過對具體空域的錄音數據分析可以得到連續管制事件的間隔時間,并按上述方法求得相應的α值,即可求得對應管制員通信工作負荷的人類動力學函數。

依據冪律函數的性質,由公式:

(10)

求得樣本的數學期望E(X),則該扇區一小時內管制事件的發生頻率為3600/E(X)。

3 基于人類動力學的終端容量預測

終端空域由若干扇區構成,而每個扇區中管制事件的發生必然與該扇區空域內的航空器數量有關,即當空域內無航空器時,管制事件就不會發生。據此,本文利用多元線性回歸分析的方法來建立各扇區的容量評估模型,最后通過綜合評定來確定整個終端空域的預測容量值(由于航路的聯系各扇區間相互關聯,終端空域容量不是簡單的將各扇區容量值相加求和得到)。多元線性回歸的基本模型為

y=β1X1+β2X2+…+βnXm+e

(11)

通過對原始數據集的分析和整理,共提取如下模型求解變量:某時段管制事件發生的次數、對應時段扇區各走廊口進出港及飛越航空器的數量、對應時段扇區內進出港及飛越航空器的數量。回歸模型的響應變量為某時段管制事件發生的次數。經線性回歸分析及求解,綜合評價了預測變量對模型的貢獻作用,本文最終選擇了三個預測變量:即對應時段扇區內的進場航空器數量、離場航空器數量和飛越航空器數量。

定義2 因變量y為單位時間內管制事件發生的次數,自變量x1、x2、x3分別為單位時間內空域中的進、離場及飛越航空器的數量。

建立的回歸方程如式(2):

y=β1x1+β2x2+β3x3+e

(12)

通過對前文所述扇區的數據的采集與處理,可以獲得回歸方程中需要的各變量值,利用多元線性回歸法可以求得相應的回歸方程。根據得到的回歸方程,分析扇區內的管制員工作負荷,并參照DORATASK方法[7]評估扇區的容量。由于DORATASK方法設定了80%的閾值標準,則評估時間內的管制事件發生頻率變為2880/E(X)。以此作為約束條件,帶入已知的回歸方程,從而確定對應扇區的空域容量。

4 算例分析

提取由成都終端空域某扇區的錄音數據分析得到1000個連續管制事件的間隔時間,通過對這些數據觀察可知管制事件具有陣發性,即在某些時段會集中發生,間隔時間短,發生的頻率高(如8h～11h、14h～17h、19h～21h),而其余時段則有較長的間歇時間。這樣的分布是符合實際的工作情況的,管制事件高發時段恰恰為實際運行單位的繁忙時段。

對已知數據進行分析,采用極大似然估計法并按照公式(9)計算得出冪指數α=2.55,并用已知冪指數為2.55的理論曲線和數據的散點圖進行類比。其分布情況及密度分布情況如圖1和圖2所示。由圖2可以明顯的觀察到管制事件間隔時間的密度分布具有明顯的重尾特性,說明其的確符合冪律分布。

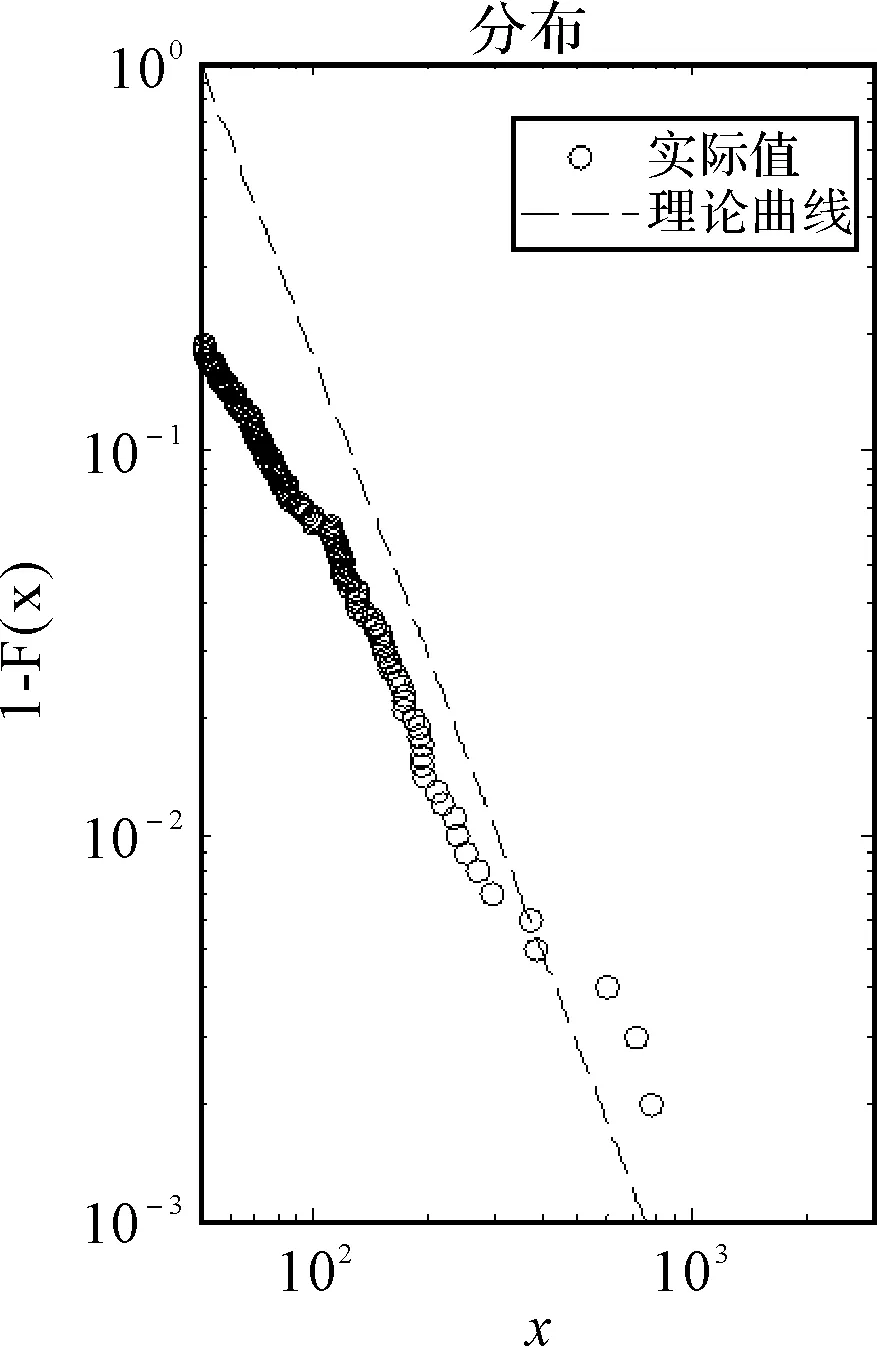
圖1 管制事件時間間隔的分布

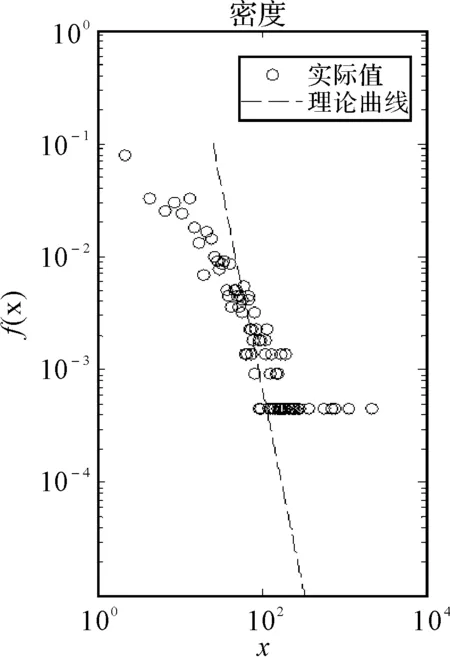
圖2 管制事件時間間隔的密度分布

經過進一步的擬合得到該樣本下的管制事件的密度函數為

f(x)=122.36x-2.55

(13)

由式(10)計算得E(X)=47.21s,則該扇區一小時內管制事件的發生頻率為3600/47.21≈76次/小時。

分析回歸方程中需要的各變量值,其中部分樣本數據如表1所示(表中數據持續時間段均為1小時)。

對總體樣本進行回歸分析,根據多元線性回歸分析的結果,確定最終的模型為

y=1.385x1+2.768x2+1.75x3

(14)

從回歸模型的系數來看,離場航空器對管制事件的發生次數影響最大,其次是飛越航空器對管制事件的影響。考慮到實際管制中區域管制室的指揮席管制員的大部分精力用于指揮從進近扇區移交過來的離場航空器,以及對飛越航空器進行扇區之間的移交,故回歸模型中系數的大小關系是合理的。

考慮成都區域雷達管制指揮席管制員的實際工作情況,可以發現管制事件是其工作的重心,與航空器之間的語音通信占據了其工作時間中的絕大部分,這部分工作包括給機長下達相關機動指令和聽機長對指令進行復述。除此之外,管制員在實際工作中還涉及很少一部分諸如拖拽標牌等主觀負荷,由于受到各管制員的行為習慣影響,所表現的主觀性較強,所以沒有在回歸模型中考慮這些因素。最后,現在實施的是雷達管制,指揮席管制員還需關注雷達顯示屏,只要管制區域內有航空器,按照規定管制員必須對其進行監視。由于監視活動很多時候是與管制事件同時發生的,故可認為管制事件中已包含此部分負荷,所以本文的模型中沒有考慮監視活動的影響。

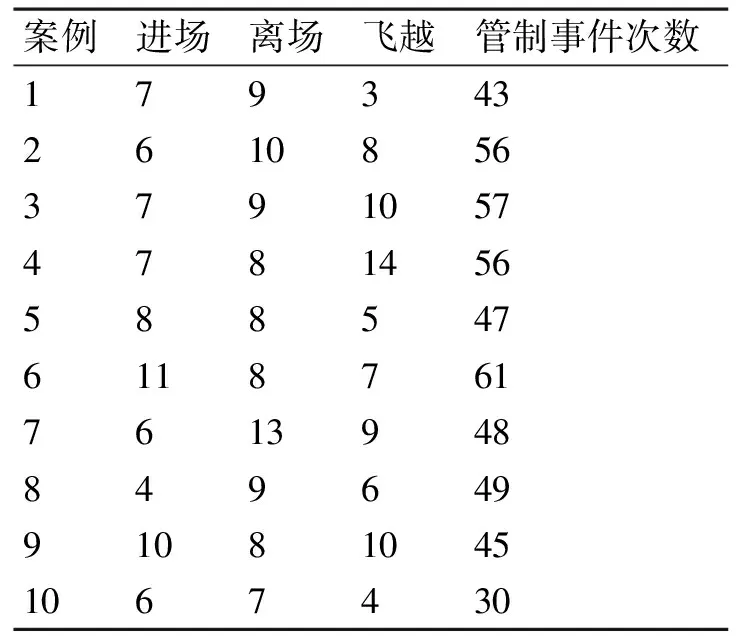
表1 部分管制事件及對應架次數據

根據得到的回歸模型(14),可以分析扇區內的管制員工作負荷。由于DORATASK方法設定了80%的閾值標準,則評估時間內的管制事件發生頻率變為2880/47.2.1≈61次/小時。

根據實際運行情況,設定進離場比例為1∶1,進離場總架次分別從25架次/小時到37架次/小時,分別計算扇區內飛越的航空器占扇區內總航空器數量的30%、40%、50%時對應的管制事件的發生次數,可得出如下結論:

1) 飛越數量占扇區內所有飛機數量的30%時,運行容量為30架次/小時;

2) 飛越數量占扇區內所有飛機數量的40%時,運行容量為31架次/小時;

3) 飛越數量占扇區內所有飛機數量的50%時,運行容量為32架次/小時。

同樣的,用此方法考察終端空域中的各個扇區,即可得到對應扇區的運行容量值,最后綜合考慮機場容量和最先達到飽和的扇區等容量限制因素,利用加權求和的方法獲得終端空域的運行容量值。

5 結語

本文研究了基于管制員工作負荷的扇區容量評估問題,將人類動力學的相關研究運用到管制員工作負荷評估研究中,并運用回歸分析的方法建立了整套的容量評估模型。與以往的研究相比較,本文簡化了模型,考慮了飛越航空器對扇區容量的影響,并簡化了數據的統計工作,增加了模型的可操作性和普適性。最后,結合成都地區的數據,驗證了模型的可行性,評估結果是合理的。

[1] 2012年全國民航運輸指標統計公報[R].中國民用航空局,2012.

[2] Doc9426-AN/924. Manual for air traffic service plan[S]. International civil aviation organization,2010.

[3] Zhou T, Kiet H A T, Kim B J, et al. Role of activity in human dynamics[J]. Europhysics Letters,2008,82(2):105-108.

[4] Clauset A, Shalizi C R, Newman M E J. Power-law distributions in empirical data[DB/OL]. [2013-11-10]. http://arxiv.org/abs/0706.1062v2.

[5] Wikipedia. Pareto_distribution[DB/OL]. [2013-11-10]. http://en.wikipedia.org/wiki/Pareto_distribution.

[6] Hong W, Han X P, Zhou T, et al. Heavy-tailed statistics in short-message communication[J]. Chinese Physics Letters,2009,26(2):132-136.

[7] 中國民航局空中交通管理局,IB-TM-2009-008,空域建模與評估實施方法指導材料[S].中國民航局空中交通管理局,2009.

[8] 彭文華,衛平凡,劉國光.基于效能的艦炮武器系統RMS指標設計方法[J].艦船電子工程,2010,30(1):172-174.

[9] 張兆寧,王莉莉.空中交通流量管理理論與方法[M].北京:科學出版社,2009:79.

The Evaluating Method of Sector Capacity Based on the Workload of ATC

REN Ming1SHAN Le2

(1. Second Department, Navy College of Command, Nanjing 210016) (2. Civil Aviation College, Nanjing University of Aeronautics and Astronautics, Nanjing 210016)

In order to accurately evaluate airspace capacity, a method was proposed to measure the workload of atc based on human dynamics, the work process of atc was determined to belong to the typical human dynamics by analyzing the characteristics of atc communication workload, and according with power law distribution. On this basis, the evaluation model of sector capacity was established by using multiple linear regression model based on the workload of atc. In the end, the accuracy of the model was verified by the case analysis.

air traffic management, capacity assessment, human dynamics

2015年4月8日,

2015年5月26日

任民,男,副教授,研究方向:兵種指揮、航空兵管制運行。閃樂,男,碩士研究生,研究方向:新一代空管自動化系統。

V355.1

10.3969/j.issn.1672-9730.2015.10.008