系泊纜等效水深截?cái)帱c(diǎn)處動(dòng)力響應(yīng)

洪文淵，張火明, 管衛(wèi)兵，高文軍，陳陽(yáng)波

(1.中國(guó)計(jì)量學(xué)院 計(jì)量測(cè)試工程學(xué)院，浙江 杭州 310018;

2.國(guó)家海洋局第二海洋研究所 衛(wèi)星海洋環(huán)境動(dòng)力學(xué)國(guó)家重點(diǎn)實(shí)驗(yàn)室，浙江 杭州 310012)

系泊纜等效水深截?cái)帱c(diǎn)處動(dòng)力響應(yīng)

洪文淵1，張火明1, 管衛(wèi)兵2，高文軍1，陳陽(yáng)波1

(1.中國(guó)計(jì)量學(xué)院 計(jì)量測(cè)試工程學(xué)院，浙江 杭州 310018;

2.國(guó)家海洋局第二海洋研究所 衛(wèi)星海洋環(huán)境動(dòng)力學(xué)國(guó)家重點(diǎn)實(shí)驗(yàn)室，浙江 杭州 310012)

摘要：考慮海洋平臺(tái)懸鏈線式系泊纜的非線性特性，采用集中質(zhì)量法建立系泊纜的運(yùn)動(dòng)方程，分別應(yīng)用時(shí)域和頻域分析方法研究系泊纜上若干節(jié)點(diǎn)的動(dòng)力響應(yīng)。分析上端點(diǎn)運(yùn)動(dòng)為正弦波動(dòng)和隨機(jī)波動(dòng)2種情況對(duì)應(yīng)的系泊纜有代表性節(jié)點(diǎn)的動(dòng)力響應(yīng)。獲得了系泊纜不同位置的等效水深截?cái)帱c(diǎn)處的動(dòng)力響應(yīng)與上端點(diǎn)的對(duì)應(yīng)規(guī)律，為進(jìn)一步研究主動(dòng)式混合模型試驗(yàn)方法提供了技術(shù)支持。

關(guān)鍵詞：系泊纜；截?cái)帱c(diǎn)；動(dòng)力響應(yīng)；集中質(zhì)量法

0引言

海上油氣資源的開(kāi)采逐步轉(zhuǎn)向深海，海洋平臺(tái)的工作水深變得越來(lái)越深。為獲得這些深海平臺(tái)的水動(dòng)力性能，通常需要進(jìn)行物理模型試驗(yàn)，而現(xiàn)有海洋工程水池的尺度卻無(wú)法容納按照常規(guī)縮尺比制作的深海平臺(tái)系統(tǒng)，此時(shí)需要采用混合模型試驗(yàn)方法[1-2]，根據(jù)全水深系統(tǒng)設(shè)計(jì)制作等效的截?cái)嘞挡聪到y(tǒng)進(jìn)行模型試驗(yàn)。混合模型試驗(yàn)方法可以分為被動(dòng)式和主動(dòng)式2種方式。由于被動(dòng)式混合模型試驗(yàn)方法存在一些難以克服的缺點(diǎn)[3]，目前希望通過(guò)主動(dòng)式方法來(lái)獲得深海平臺(tái)系統(tǒng)的水動(dòng)力性能參數(shù)。

主動(dòng)式混合模型試驗(yàn)方法的基本原理如圖1所示。該方法根據(jù)水池所能模擬的深度在其池底用1套計(jì)算機(jī)伺服機(jī)構(gòu)實(shí)時(shí)模擬出系泊纜/立管在截?cái)帱c(diǎn)處的運(yùn)動(dòng)和受力，其優(yōu)點(diǎn)是能夠直接通過(guò)模型試驗(yàn)去獲得所需的結(jié)果。

圖1　主動(dòng)式混合模型試驗(yàn)示意圖Fig.1　Schematic active style hybrid model testing

要實(shí)現(xiàn)主動(dòng)式混合模型試驗(yàn)方法，其首要的工作是要精確計(jì)算截?cái)帱c(diǎn)處的運(yùn)動(dòng)和受力情況，通常有多種方法可供選擇，本文選取理論簡(jiǎn)單、編程方便、應(yīng)用廣泛的集中質(zhì)量法[4]。很多國(guó)內(nèi)外專家學(xué)者基于該方法得到了一些有意義的結(jié)論[5-8]。

本文針對(duì)海洋平臺(tái)懸鏈線式的系泊纜，忽略一些影響較小的因素，主要考慮流體阻力和幾何特性等非線性因素，在此基礎(chǔ)上采用集中質(zhì)量法對(duì)非線性、多自由度的系泊纜動(dòng)力特性進(jìn)行研究，為主動(dòng)式混合模型試驗(yàn)以及國(guó)內(nèi)海洋平臺(tái)的發(fā)展提供一定技術(shù)支持和幫助。

1系纜動(dòng)力分析數(shù)學(xué)模型

采用集中質(zhì)量法對(duì)懸鏈線式系泊纜索建立數(shù)學(xué)模型，這里僅考慮系纜在xoz平面下的形變(見(jiàn)圖2)，以海平面上指向浮體的方向?yàn)閤軸正方向，垂直于海平面向上為z軸正方向。將系纜分為N段，則總共N+1個(gè)節(jié)點(diǎn)。除去上下2個(gè)端點(diǎn)，其余節(jié)點(diǎn)的質(zhì)量為前后2段系纜單元重量和的一半，根據(jù)系纜節(jié)點(diǎn)受力分析，由牛頓第二定律可得到第j個(gè)節(jié)點(diǎn)的運(yùn)動(dòng)方程如下[9]：

(1)

(2)

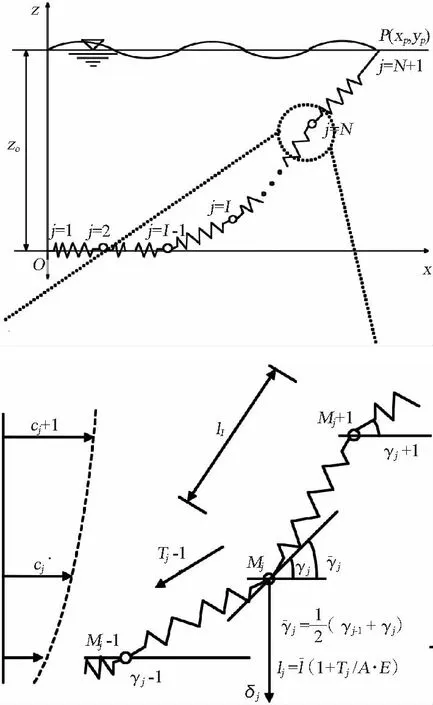
圖2　系泊纜集中質(zhì)量模型Fig.2　Model of lumped-mass mooring line

(3)

(4)

式中：Dc為系纜元的直徑；lj為系纜元的長(zhǎng)度；Tj為第j和j+1個(gè)節(jié)點(diǎn)之間系纜元的張力；γj為第j個(gè)節(jié)點(diǎn)與水平方向的夾角；σj為第j個(gè)節(jié)點(diǎn)的修正后的重量；fdxj和fdzj分別為作用在第j個(gè)節(jié)點(diǎn)上的水平和垂直方向的流體阻力，可用Morrision公式[10]求得：

(5)

式中：Cdt為垂向和切向阻力系數(shù)；unj和utj為相對(duì)速度分量；Cdx和Cdz分別為浮筒或重物對(duì)應(yīng)的阻力系數(shù)；Arx和Arz分別為浮筒或重物在x軸和z軸方向上的投影面積。若無(wú)浮筒或重物，劃線部分不計(jì)。

運(yùn)動(dòng)方程(1)和(2)的求解過(guò)程中存在數(shù)值積分，選用Houbolt差分格式[11]求解，若標(biāo)記n為當(dāng)前值，記n+1為下一計(jì)算時(shí)間步長(zhǎng)后的值，則速度和加速度的差分記作：

(6)

解方程時(shí)所需的初始值取為靜平衡狀態(tài)時(shí)纜索形狀和張力，采用文獻(xiàn)[12]方法計(jì)算得到。本文就上述理論編寫(xiě)計(jì)算系泊動(dòng)力的C++程序，并對(duì)下面的算例進(jìn)行了驗(yàn)證計(jì)算。給定系泊纜的等效直徑為0.005 99 m，系泊纜長(zhǎng)9 m，水深3 m，纜索的彈性模量為2.107×1010N/m3，初始預(yù)張力為28.488 6 N，海水的密度為1 030 kg/m3，時(shí)間步長(zhǎng)為0.02 s，水流速度為0.5 m/s。當(dāng)給定上端點(diǎn)的激勵(lì)為x軸方向上的簡(jiǎn)諧運(yùn)動(dòng)時(shí)，將程序計(jì)算結(jié)果和文獻(xiàn)[13]中的試驗(yàn)結(jié)果進(jìn)行比較(見(jiàn)圖3)，發(fā)現(xiàn)二者符合程度較好，整體趨勢(shì)、大小都非常吻合。

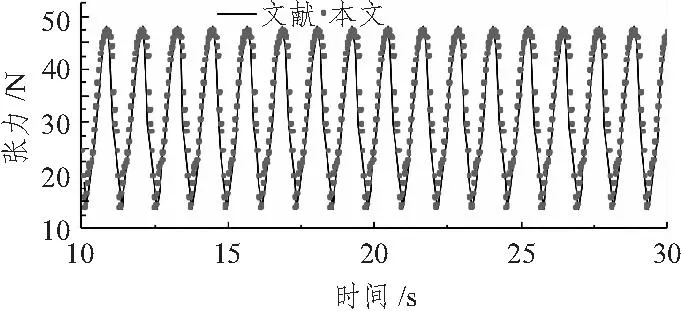
圖3　計(jì)算結(jié)果驗(yàn)證圖Fig.3　Validation figure of calculation results

2算例分析

2.1　算例描述

以一工作水深320 m的FPSO系泊纜為研究對(duì)象，給定系泊纜的長(zhǎng)度1 040 m，初始預(yù)張力3.0×105N，海水密度1 025 kg/m3，平均水流速度1 m/s。從錨碇到浮體系纜樁按材質(zhì)的不同將纜索分為3種分段，各材質(zhì)分段的局部分段數(shù)分別為60，32，12，總共N=104段；包括上端點(diǎn)，總共105個(gè)集中質(zhì)量點(diǎn)，并假設(shè)每段的質(zhì)量都集中在2個(gè)端點(diǎn)上；等效直徑分別為126 mm，101.6 mm和101.6 mm，纜索的彈性模量為分別為9.339 1×1010N/m2，1.1×1011N/m2和1.1×1011N/m2；每段纜長(zhǎng)度為10 m，時(shí)間步長(zhǎng)Δt=0.000 1 s。每段系泊纜受重力、浮力及流體阻力等外作用的影響。這里假設(shè)海底水平，計(jì)算得到系纜在靜平衡狀態(tài)下的形狀如圖4所示，前60個(gè)節(jié)點(diǎn)基本處于躺底狀態(tài)，因此下面將主要針對(duì)第60個(gè)以后的節(jié)點(diǎn)進(jìn)行分析。靜平衡狀態(tài)下的張力如圖5所示。

圖4　系泊纜靜態(tài)形狀Fig.4　Static shape of mooring line

圖5　系泊纜靜態(tài)張力Fig.5　Static tension of mooring line

2.2　數(shù)值試驗(yàn)及結(jié)果分析

2.2.1上端點(diǎn)的運(yùn)動(dòng)為正弦波情況

給定浮體上端點(diǎn)的運(yùn)動(dòng)為X=Asin(ωt)(A為振幅)，定義系泊纜第i(i=1,2,3,…,N+1)個(gè)節(jié)點(diǎn)對(duì)應(yīng)的張力頻率響應(yīng)函數(shù)為RAO，即

(7)

其中，Si(ω)為張力對(duì)應(yīng)的功率密度譜函數(shù)，如果已經(jīng)獲知上端點(diǎn)張力的功率譜，那么可以由該式計(jì)算出纜索相應(yīng)節(jié)點(diǎn)的張力譜，再通過(guò)頻域時(shí)域轉(zhuǎn)換就可以獲知其時(shí)域中張力時(shí)歷，這對(duì)主動(dòng)式混合模型試驗(yàn)方法很有幫助，該方法在實(shí)施過(guò)程中需及時(shí)獲取截?cái)帱c(diǎn)處運(yùn)動(dòng)及受力情況。取系泊纜上第75，83，92和100個(gè)節(jié)點(diǎn)作為代表進(jìn)行計(jì)算，這些點(diǎn)可假想為主動(dòng)式混合模型試驗(yàn)方法中等效水深截?cái)帱c(diǎn)，當(dāng)振幅A=1 m時(shí)，得到對(duì)應(yīng)張力T的頻率響應(yīng)曲線如圖6所示，可以看出，第75，83，92和100個(gè)節(jié)點(diǎn)走勢(shì)大致相同，在頻率900 rad/s之前，整體呈上升趨勢(shì)，隨后開(kāi)始下降，頻率大于1 000 rad/s之后，四者形態(tài)都呈現(xiàn)出平穩(wěn)的趨勢(shì)。圖7反映的是在不同頻率下上端點(diǎn)張力最大值和最小值的變化趨勢(shì)，分別計(jì)算A=1 m，A=15 m和A=32 m三種情況，可以看出，隨著系泊纜頂端運(yùn)動(dòng)時(shí)歷的運(yùn)動(dòng)幅值增大，系泊纜對(duì)應(yīng)的最大張力和最小張力的變化幅度也變大。而隨著頻率的增大，3種振幅情況下張力的大小也都呈現(xiàn)出單調(diào)遞增的趨勢(shì)。

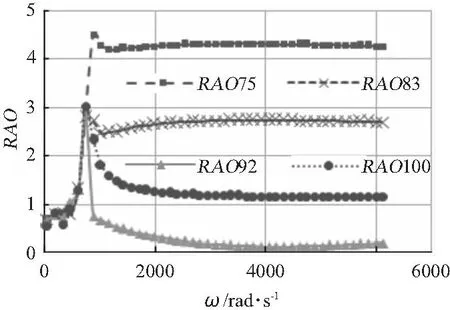
圖6　張力T的頻率響應(yīng)曲線Fig.6　Frequency response curve of T

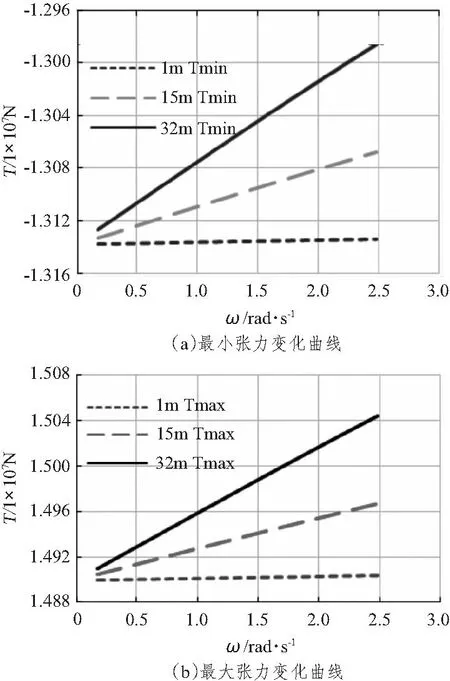
圖7　張力-頻率曲線Fig.7　Tension-Frequency curve

2.2.2上端點(diǎn)的運(yùn)動(dòng)為隨機(jī)波情況

浮體上端點(diǎn)的運(yùn)動(dòng)采用類似于隨機(jī)波浪的數(shù)值方法生成[14]，公式如下：

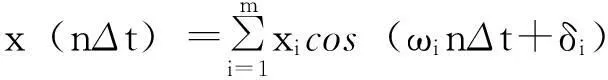
(8)

γexp[-(Tpf-1)2/2σ2]。

(9)

式中：S(f)為譜密度，m2/s；α為能量尺度參數(shù)；f為波頻，Hz；g為重力加速度，m/s2；Tp為譜峰周期，s；fp=1/Tp；γ為譜峰升高因子。當(dāng)f>fp時(shí)，σ為0.09；f

功率譜曲線如圖8所示，上端點(diǎn)的運(yùn)動(dòng)時(shí)歷曲線如圖9所示。

圖8　波浪譜曲線Fig.8　Wave spectrum curve

圖9　上端運(yùn)動(dòng)時(shí)歷曲線Fig.9　Time shifts curve of endpoint

分別選第75,83,92和100個(gè)節(jié)點(diǎn)進(jìn)行計(jì)算分析，在已知上端點(diǎn)的運(yùn)動(dòng)情況下，分別計(jì)算得到對(duì)應(yīng)各截?cái)帱c(diǎn)處的張力時(shí)歷曲線，如圖10所示。

圖10　截?cái)帱c(diǎn)對(duì)應(yīng)的張力時(shí)歷曲線圖Fig.10　Time tension curve of truncated points

同時(shí)計(jì)算得到如圖11所示的一系列張力譜對(duì)比圖。從圖中可看出，不同節(jié)點(diǎn)對(duì)應(yīng)的系泊纜的張力譜與系泊纜上端點(diǎn)的張力譜趨勢(shì)基本相同，總的來(lái)說(shuō)，越靠底部的節(jié)點(diǎn)其譜峰值和譜包絡(luò)面積就越小。圖12給出了各個(gè)節(jié)點(diǎn)在不同情況下的運(yùn)動(dòng)軌跡，可以看出，雖然給定上端點(diǎn)的運(yùn)動(dòng)為水平單一方向上的運(yùn)動(dòng)，但水下系泊纜各節(jié)點(diǎn)的運(yùn)動(dòng)存在著橫縱2個(gè)方向上的運(yùn)動(dòng)，雖然各個(gè)節(jié)點(diǎn)的運(yùn)動(dòng)狀態(tài)都不一樣，但其整體運(yùn)動(dòng)范圍卻都非常接近。

圖11　系泊纜各截?cái)帱c(diǎn)張力功率譜密度函數(shù)Fig.11　Tension power spectral density functions of each　truncated point of the mooring line

圖12　系泊纜各截?cái)帱c(diǎn)運(yùn)動(dòng)軌跡Fig.12　Motion tracks of each truncated point of the mooring line

3結(jié)語(yǔ)

本文基于集中質(zhì)量法對(duì)系泊纜的動(dòng)力特性進(jìn)行分析，同時(shí)建立了時(shí)域運(yùn)動(dòng)方程，用C++語(yǔ)言編寫(xiě)了相應(yīng)的計(jì)算機(jī)程序。研究了2種不同起步算法對(duì)系泊纜有代表性節(jié)點(diǎn)的動(dòng)力特性的影響，同時(shí)分析了系泊纜不同節(jié)點(diǎn)(假想截?cái)帱c(diǎn))的動(dòng)力響應(yīng)與上端點(diǎn)之間的對(duì)應(yīng)關(guān)系。研究結(jié)果表明：

1)集中質(zhì)量法用于該問(wèn)題行之有效；

2)不同節(jié)點(diǎn)對(duì)應(yīng)的系泊纜張力譜與系泊纜上端點(diǎn)張力譜趨勢(shì)基本相同，越靠底部的節(jié)點(diǎn)其譜峰值和譜包絡(luò)面積就越小；

3)雖然各個(gè)節(jié)點(diǎn)的運(yùn)動(dòng)狀態(tài)都不一樣，但是其整體運(yùn)動(dòng)范圍卻都非常接近。

在進(jìn)一步工作中可選擇繃緊式系泊系統(tǒng)作為研究對(duì)象，能夠更好的為主動(dòng)式混合模型試驗(yàn)方法中系泊纜等效水深截?cái)帱c(diǎn)處的動(dòng)力響應(yīng)模擬提供技術(shù)支持。

參考文獻(xiàn)：

[1]STANSBERG C T,ORMBERG H,ORITSLAND O.Challenges in deep water experiments:hybrid approach[J].Journal of Offshore Mechanics and Arctic Engineering,2002,124:90-96.

[2]張火明,楊建民,肖龍飛.深海海洋平臺(tái)混合模型試驗(yàn)技術(shù)研究與進(jìn)展[J].中國(guó)海洋平臺(tái),2004,19(5):1-6.

ZHANG Huo-ming,YANG Jian-min,XIAO Long-fei.A view on the hybrid model test technique for deep sea platform[J].China Offshore Platform,2004,19(5):1-6.

[3]盛振邦,肖龍飛.深海海洋平臺(tái)混合模型試驗(yàn)技術(shù)[J].上海造船,2003(1):12-14.

SHENG Zhen-bang,XIAO Long-fei.Hybrid model test technique for deep sea platform[J].Shanghai Shipbuliding,2003(1):12-14.

[4]唐友剛,張若瑜,程楠,等.集中質(zhì)量法計(jì)算深海系泊沖擊張力[J].天津大學(xué)學(xué)報(bào),2009,42(8):696-701.

TANG You-gang,ZHANG Ruo-yu,CHENG Nan,et al.Analysis of snap tension of deep water mooring with lumped mass method[J].Journal of Tianjin University,2009,42(8):696-701.

[5]HUANG S,VASSALOS D.Snap loading of marine cables[C]//The Proceedings of the International Offshore and Polar Engineering Conference.International Society of Offshore and Polar Engineers,1994:304-310.

[6]RAMAN-NAIR W,BADDOUR R E.Three-dimensional dynamics of a flexible marine riser undergoing large elastic deformations[J].Multibody System Dynamics,2003,10(4):393-423.

[7]聶孟喜,王旭升,張琳.單錨腿系泊系統(tǒng)動(dòng)力響應(yīng)的時(shí)域計(jì)算方法[J].海洋工程,2004,22(2):58-61.

NIE Meng-xi,WANG Xu-sheng,ZHANG Lin.An time domain approach to computing dynamic response of a single anchor[J].The Ocean Engineering,2004,22(2):58-61.

[8]程楠.集中質(zhì)量法在深海系泊沖擊張力計(jì)算中的應(yīng)用研究[D].天津:天津大學(xué),2008.

CHENG Nan.Study on application of lump-mass method to calculating snap mooring tension in the deep sea[D].Tianjin：Tianjin University,2008.

[9]COZIJN J L,BUNNIK T H J.Coupled mooring analysis for a deep water CALM buoy[C]//ProcConf Offshore Mech and ArctEng,2004.

[10]聶孟喜,王旭升,王曉明，等.風(fēng)、浪、流聯(lián)合作用下系統(tǒng)系泊力的時(shí)域計(jì)算方法[J].清華大學(xué)學(xué)報(bào)(自然科學(xué)版),2004,44(9):1214-1217.

NIE Meng-xi,WANG Xu-sheng,WANG Xiao-ming,et al.Time domain approach for computing the mooring force of a mooring system subject to wind, waves and currents[J].Journal of Tsinghua University(Science and Technology),2004,44(9):1214-1217.

[11]張雄,王天舒.計(jì)算動(dòng)力學(xué)論[M].北京：清華大學(xué)出版社,2007：140-207.

ZHANG Xiong,WANG Tian-shu.Computational dynamics[M].Beijing：Tsinghua University Press,2007：140-207.

[12]張火明，張曉菲，楊建民.基于優(yōu)化思想的多成分系泊纜靜力特性分析[J].艦船科學(xué)技術(shù),2010,32(10):114-121.

ZHANG Huo-ming,ZHANG Xiao-fei,YANG Jian-min.Static characteristic analysis of multi-component mooring line based on optimization thinking[J].Ship Science and Technology,2010,32(10):114-121.

[13]NAKAJIMA T.On the dynamic analysis of multi-component mooring lines[C].The 14thAnnual Offshore Technology Conference,1982.

[14]蘇一華，楊建民，肖龍飛.深海平臺(tái)試驗(yàn)中水深截?cái)嘞挡蠢|動(dòng)力特性對(duì)比分析[J].海洋工程,2009,27(1):17-21.

SU Yi-hua,YANG Jian-min,XIAO Long-fei.A comparative analysis of dynamic characteristics of truncated mooring lines in deepwater platform model test[J].The Ocean Engineering,2009,27(1):17-21.

[15]俞聿修.隨機(jī)波浪及其工程應(yīng)用[M].大連: 大連理工大學(xué)出版社,2000.

YU Yu-xiu.Random wave and its applications to engineering[M].Dalian：Dalian University of Technology Press,2000.

The dynamic response analysis of the equivalent water depth truncated point of the mooring line

HONG Wen-yuan1,ZHANG Huo-ming1,Guan Wei-bing2,GAO Wen-jun1,CHEN Yang-bo1

(1.College of Metrology and Measurement Engineering, China Jiliang University,Hangzhou 310018,China;

2.State Key Laboratory of Satellite Ocean Environment Dynamics,Second Institute of Oceanography,

State Oceanic Administration,Hangzhou 310012,China)

Abstract：In this paper, considering the nonlinear characteristics of the sea platform catenary mooring line, the equations of the mooring line motion are formulated by using lumped-mass method and the dynamic response of some points on mooring line is investigated by the time and frequency domain analysis method. The dynamic response of the representative point on the mooring line is analyzed by giving two different corresponding upper endpoint movements which are sine wave excitation and random wave excitation. The corresponding laws of the dynamic response between the equivalent water depth truncated points at different locations and the upper endpoint are obtained, which can provide technical support for further study of the active hybrid model testing technique.

Key words：mooring line;truncated point;dynamic response;lumped-mass method

作者簡(jiǎn)介：洪文淵(1989-)，男，碩士研究生，研究方向?yàn)榱黧w檢測(cè)與仿真技術(shù)。

基金項(xiàng)目：國(guó)家自然科學(xué)基金資助項(xiàng)目(51379198)；浙江省青年科學(xué)家培養(yǎng)計(jì)劃資助項(xiàng)目(2013R60G7160040)

收稿日期：2013-12-31； 修回日期： 2014-02-25

文章編號(hào)：1672-7649(2015)01-0023-06

doi：10.3404/j.issn.1672-7649.2015.01.005

中圖分類號(hào)：P751

文獻(xiàn)標(biāo)識(shí)碼：A