一種螺旋槳參數化建模方法

張以良，熊　鷹，時立攀

(海軍工程大學 艦船與海洋工程系，湖北 武漢 430033)

一種螺旋槳參數化建模方法

張以良，熊鷹，時立攀

(海軍工程大學 艦船與海洋工程系，湖北 武漢 430033)

摘要：對螺旋槳進行優化時，需要建立起優化計算的樣本空間，即要實現初始槳的參數化建模。本文基于貝塞爾曲線擬合原理編程實現了螺旋槳的參數化建模，對螺旋槳的徑向參數分布分別用一條貝塞爾曲線進行擬合，曲線的控制點通過遺傳算法尋優求得。文中以4382槳為例，對其進行參數化建模，討論了三、四、五、六階貝塞爾曲線的擬合效果，發現三階貝塞爾曲線擬合光順性最好、擬合平均誤差可以控制在0.3%以內，而且控制點個數較少，最適合擬合螺旋槳徑向參數分布。最后通過調整三次貝塞爾曲線控制點的位置調整了原槳葉的幾何形狀，得到光順性較好的新槳葉模型，表明該參數化建模方法合理。

關鍵詞：螺旋槳；參數化建模；貝塞爾曲線；遺傳算法

0引言

隨著船舶向大型化、快速化發展，船舶對螺旋槳綜合性能的要求越來越高。傳統的圖譜設計和理論設計方法在進行螺旋槳設計時均無法綜合考慮螺旋槳的各性能要求，設計出的槳往往達不到綜合性能的最優。因而，通過智能優化算法對螺旋槳的綜合性能進行優化的研究越來越多[1-2]。對螺旋槳進行優化時，需要建立起優化計算的樣本空間，即要對初始槳的幾何形狀形成一種較為合理的參數化表達方式，以便通過參數調整自動生成幾何形狀不同的螺旋槳。該表達方式必須滿足以下2個原則：一是準確描述初始槳形狀，且表達參數的個數不能過多，否則優化時間過長、優化效果不理想；二是必須保證生成的樣本空間中的螺旋槳幾何形狀光順。

對螺旋槳幾何形狀進行描述的普遍方法是給出其幾何參數表，通過公式轉換可將這些參數轉換為三維空間坐標點，將其導入三維軟件可以建立螺旋槳的幾何模型[3]。幾何參數表給出了螺旋槳的剖面翼型和徑向參數分布，徑向參數包括弦長、螺距、總縱傾、側斜、最大厚度、最大拱度。可以考慮在保持剖面翼型不變的情下，對其徑向參數分布進行擬合，進而調整擬合曲線形狀從而實現對螺旋槳幾何形狀的調整。

貝塞爾曲線擬合可以在滿足上述2條原則的情況下實現徑向參數分布的擬合。每條n階貝塞爾曲線的形狀由n+1個控制點進行控制[4]，控制點個數對于優化可以接受。并且，貝塞爾曲線的控制點對整條曲線具有較強的全局控制能力[5]，改變一個控制點會使整條曲線的形狀發生調整。這種性質可以保證調整后徑向參數分布的合理性，即可以保證調整后的槳葉模型的光順性。每個控制點可進行(X和Y)2個方向的變化，這樣，螺旋槳的幾何形狀就由控制點的位置來進行控制，實現螺旋槳的參數化建模。尋求擬合曲線控制點位置是參數化建模的關鍵，本文利用遺傳算法，用優化的手段尋得了控制點位置，擬合的效果和精度令人滿意。

1貝塞爾曲線

貝塞爾曲線模型由雷諾汽車公司的法國工程師Bezier于1962年提出，在幾何設計中有廣泛的應用[6-8]。1條貝塞爾曲線由控制多邊形確定，并且具有插值控制多邊形首末控制點的性質[9]。1條三次貝塞爾曲線及其控制多邊形如圖1所示。

圖1　三次貝塞爾曲線及其控制多邊形Fig.1　Three order bezier curve and the control polygon

n階貝塞爾曲線方程的矩陣形式如下[10]：

P(u)=[(1-u)nn(1-u)n-1u…

(1)

式中：u為參數，u∈[0,1]；Vi為控制點，i=0,1,2,…,n。

2基于遺傳算法的控制點求解

遺傳算法不依賴于問題所屬的具體領域，提供了一種求解非線性、多模型、多目標等復雜系統優化問題的通用框架[11]，應用非常廣泛[12-13]。本文利用Matlab專門設計的遺傳算法與直接搜索工具箱(GADS)尋求擬合貝塞爾曲線的控制點，得到了很好的效果。

2.1　優化變量的選取

由貝塞爾曲線插值控制多邊形首末控制點的性質可知，一條貝塞爾曲線的首末控制點即為要擬合數據點的首末端點。本文選取首末以外的控制點的X和Y坐標的變化量為優化變量，新的控制點坐標為原控制點坐標與其對應的變化量之和。

2.2　目標函數的建立

GADS總是試圖尋找適應度函數的最小值，本文以擬合曲線與對應半徑處原參數值誤差的絕對值的最大值為目標函數：

f(x)=max(abs(FP-P))。

(2)

式中：x為變量，此處為要求的2個控制點X和Y坐標的變化量；P為原各半徑處參數的值；FP為擬合曲線上對應原各半徑處參數的值。

2.3　約束條件的設置

為保證生成的曲線不會出現纏繞等不合理的現象，需要對生成的控制點的位置進行限制，約束條件為：

0≤VX1≤VX2≤…VXi-1≤VXi≤1。

(3)

式中VXi為擬合曲線控制點的X坐標值

當出現不符合式(3)所示的情況時，取目標函數的值等于100，就可以保證最終得到的擬合曲線的合理性。

3不同階次貝塞爾曲線的擬合比較

本文分別用3~6階貝塞爾曲線擬合了4382槳的徑向參數分布，觀察擬合曲線形狀判斷其光順性，用擬合最大誤差E和擬合平均誤差Ea來對擬合效果進行定量分析，其定義如下：

E=max(abs(FP-P))，

(4)

(5)

式中：P為原各半徑處參數的值；FP為擬合曲線上對應原各半徑處參數的值；n為擬合數據點的個數。

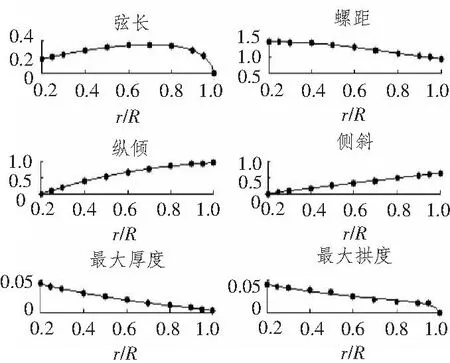
圖2　三階貝塞爾曲線擬合效果Fig.2　The fitting of three order bezier curve

圖3　四階貝塞爾曲線擬合效果Fig.3　The fitting of four order bezier curve

圖4　五階貝塞爾曲線擬合效果Fig.4　The fitting of five order bezier curve

圖5　六階貝塞爾曲線擬合效果Fig.5　The fitting of six order bezier curve

各階貝賽爾曲線擬合效果如圖2~圖5所示，觀察可發現，3~6階貝塞爾曲線都比較準確地擬合了原徑向參數點。其中，3階貝塞爾曲線擬合的光順性最好。4階貝塞爾曲線在擬合最大厚度分布時，擬合曲線在葉根附近出現了凸點。5階貝塞爾曲線在擬合最大拱度分布時，曲線光順性明顯變差。6階貝塞爾曲線擬合縱傾、最大厚度和最大拱度時光順性都比較差。

圖6　三階貝塞爾曲線擬合誤差Fig.6　The fitting error of three order bezier curve

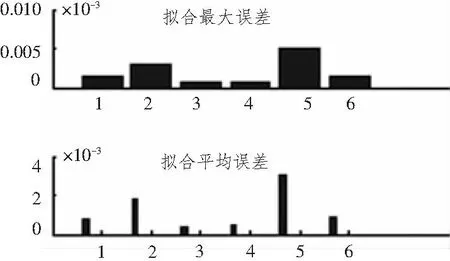
圖7　四階貝塞爾曲線擬合誤差Fig.7　The fitting error of four order bezier curve

圖8　五階貝塞爾曲線擬合誤差Fig.8　The fitting error of five order bezier curve

圖9　六階貝塞爾曲線擬合誤差Fig.9　The fitting error of six order bezier curve

圖6~圖9顯示了不同階次貝塞爾曲線的擬合最大誤差和擬合平均誤差，橫坐標1~6分別表示弦長分布、螺距分布、縱傾分布、側斜分布、最大厚度分布和最大拱度分布擬合。4階和6階貝塞爾曲線的擬合最大誤差明顯高于3階和5階貝塞爾曲線。3階和5階貝塞爾曲線的擬合最大誤差均可控制在0.4%以內，3階貝塞爾曲線的擬合平均誤差在0.3%以內，5階貝塞爾曲線的擬合平均誤差在0.2%以內。

綜上所述，3階貝塞爾曲線擬合的光順性最好，其擬合誤差僅略低于5階貝塞爾曲線，完全能夠滿足一般工程計算的需求。且貝塞爾曲線控制點個數隨其階次增加而增加，沒有必要采用高于3階的貝塞爾曲線進行徑向參數分布的擬合。故本文選用3階貝塞爾曲線進行徑向參數分布的擬合，實現螺旋槳的參數化建模。

44382槳的參數化建模

用三次貝塞爾曲線對4382槳進行參數化的建模，得到的控制點矩陣如下：

V=

(6)

矩陣V從第1列~第6列分別對應于擬合弦長、螺距、總縱傾、側斜、最大厚度、最大拱度的徑向分布曲線的控制點。每1列的前4個數據和后4個數據分別為第1~第4個控制點的X和Y坐標值。

進行優化時，不同優化算法用不同的方法會對控制點進行調整，從而生成優化計算的樣本空間。為驗證該方法的可行性，現對控制點進行一次調整，調整矩陣如下：

(7)

調整后的控制矩陣

Va=V+x。

圖10　調整前后的徑向參數分布Fig.10　Radial parameters distribution before　and after adjustment

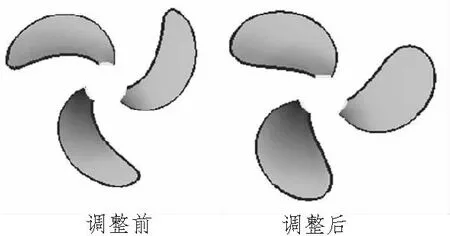
圖11　調整前后的螺旋槳三維模型Fig.11　Three-dimensional model of the propeller before　and after adjustment

調整前后的徑向參數分布如圖10所示，調整后的各徑向參數分布曲線仍具有良好的光順性。利用三維軟件建立調整前后的螺旋槳三維模型，如圖11所示，調整后的槳葉形狀合理，并且具有良好的光順性。這都表明本文提出的螺旋槳的參數化建模方法可行。

5結語

本文討論了3~6階貝塞爾曲線擬合螺旋槳徑向參數分布的效果，利用遺傳算法尋求貝塞爾曲線的控制點，發現3階貝塞爾曲線擬合光順性最好、最大擬合誤差在0.4%以內，擬合平均誤差在0.3%以內，而且控制點個數最少，最適合擬合螺旋槳徑向參數分布。最后利用三次貝塞爾曲線實現了4382槳的參數化建模，通過調整控制點的位置調整了原槳葉的幾何形狀，得到了光順性較好的新槳葉模型，表明該參數化建模方法合理有效，為今后螺旋槳的優化打下了基礎。

參考文獻：

[1]王超，熊鷹，何苗,等.粒子群算法在大側斜螺旋槳側斜分布優化中的應用[J].上海交通大學學報,2012，46(3)：398-409.

WANG Chao,XIONG Ying,HE Miao,et al.Application of particle swarm optimization theory in skew distribution of highly skewed propeller[J].Journal of Shanghai Jiao Tong University，2012，46(3)：398-409.

[2]余龍.基于CFD技術的導管螺旋槳自動優化設計技術研[J].水動力學研究與進展,2013,28(4)：438-444.

YU Long.Research on automatic optimization of ducted propeller design based on CFD techniques[J].Chinese Jounal of Hydrodynamics，2013,28(4)：438-444.

[3]唐英，王志堅，楊凱.基于UG二次開發的船用螺旋槳參數化建模方法與實現[J].船舶工程，2010，32(4):52-55.

TANG Ying，WANG Zhi-jian，YANG Kai.Parametrical modeling method and implementation of marine propeller based on UG software[J].Ship Engineering，2010，32(4)：52-55.

[4]朱心雄.自由曲線曲面造型技術[M].北京：科學出版社，2000.

[5]RONALD G.An integrated introduction to computer graphics and geometric modeling[M].CRC Press，2011.

[6]熊運陽.貝塞爾曲線的表示集及其應用[C]//第六屆全國幾何設計與計算學術會議，2013.

XIONG Yun-yang.The expression and application of bezier curve[C]//CSIAM Geometric Design & Computing，2013.

[7]付鵬飛.貝塞爾曲線在汽車設計中的運用[J].企業技術開發，2012，31(26)：46-47，91.

FU Peng-fei.The application of bezier curve on automobile design[J].Technological Development of Enterprise，2012，31(26)：46-47，91.

[8]尚仁操，喬渭陽.基于參數法和貝塞爾曲線的渦輪葉片造型及其優化[J].機械設計與制造，2007(8).

SHANG Ren-cao，QIAO Wei-yang.Turbine blade design and optimization based on the combination of parametric-bezier curve[J].Machinery Design and Manufacture，2007(8).

[9]施法中.計算機輔助幾何設計與非均勻有理B樣條[M].北京：高等教育出版社，2001.

[10]吉貝·德芒熱，讓皮爾·晡熱.曲線與曲面的數學[M].王向東，譯.北京：商務印書館,2000.

[11]雷英杰，張善文，李繼武，等.MATLAB遺傳算法工具箱及應用[M].西安：西安電子科技大學出版社，2005.

[12]黃樹權.基于遺傳算法的螺旋槳性能優化研究[D].大連：大連理工大學,2009.

HUANG Shu-quan.The research of optimization design of propeller performance based on genetic algorithm[D].Dalian：Dalian University of Technology，2009.

[13]任超，吳偉，黃征凱，等.基于遺傳算法的RBF神經網絡在GPS高程擬合中的應用[J].測繪科學，2013，38(2)：77-79.

REN Chao，WU Wei，HUANG Zheng-kai，et al.Application of RBF neural network to GPS elevation fitting based on genetic algorithm[J].Science of Surveying and Mapping，2013，38(2)：77-79.

A method of propeller parametric modelling

ZHANG Yi-liang,XIONG Ying,SHI Li-pan

(Department of Naval Architecture，Naval University of Engineering，Wuhan 430033，China)

Abstract：A method of propeller parametric modeling is needed to establish the sample space for optimization calculation in propeller optimization. Propeller parametric modeling is realized by programing based on the principle of bezier curve fitting. Every radial parameter distribution of the propeller is fitted by a bezier curve. The control points can be exactly found by genetic algorithm. Parametric modeling of propeller 4382 is established by the method, and the fitting effects of three, four, five and six order bezier curve are discussed. The fitting fairness of three order bezier curve is the best, and the mean error is less than 0.3%. Finally, the original geometry of the propeller is adjusted by adjusting the control points of the curve. The geometry of the propeller after adjustment is fairing, the result shows that the method is reasonable.

Key words：propeller;parametric modeling;bezier curve;genetic algorithm

作者簡介：張以良(1990-)，男，碩士研究生，研究方向為船舶與海洋結構物設計流體力學。

基金項目：海洋工程國家重點實驗室研究基金資助項目(1106)

收稿日期：2013-11-13； 修回日期： 2013-12-02

文章編號：1672-7649(2015)01-0034-05

doi：10.3404/j.issn.1672-7649.2015.01.007

中圖分類號：U644.33

文獻標識碼：A