基于混沌分析法的艦船電力系統穩定性研究

馬洪濤

(江蘇海事職業技術學院，江蘇 南京 211170)

基于混沌分析法的艦船電力系統穩定性研究

馬洪濤

(江蘇海事職業技術學院，江蘇 南京 211170)

摘要：對艦船電力系統進行分析建模，并根據電力系統模型狀態的非線性混沌特征，結合模型幅值擾動參數，分析出混沌現象產生的原因和影響因素。在此基礎上，有針對性地利用自適應反演算法在模型中引入適當的控制器，有效地避免電力系統運行中因干擾進入混沌震蕩狀態，保證了艦船電力系統的正常運行和艦船的安全穩定。研究結果表明，即使艦船電力系統出現混沌現象時，也可以根據其特征狀態進行有效的穩定性控制，保持艦船的綜合性能。

關鍵詞：混沌分析；電力系統；穩定性

0引言

艦船噸位的增加和艦船結構設計的復雜給艦船設備制造提出了更高要求。隨著電力電子技術、信息技術、計算機技術的廣泛應用，大量的艦船設備中都嵌入了這些新技術以完善綜合控制系統的智能型和靈敏性。在艦船控制系統中，尤其是電力系統扮演著艦船生命力的角色，成為艦船綜合性能評價的關鍵[1-2]，因此，對艦船電力系統的研究也隨著認識程度不斷深入。在艦船動力系統中，因電力電子器件的物理特性會造成電力系統工作的非線性震蕩現象產生，這些現象在一定程度上影響著艦船性能的穩定。而非線性中的混沌現象由于其無規則、無周期、無目的性給艦船的運行帶來威脅。因此對艦船電力系統的混沌現象進行研究，最大限度地進行預防控制，保持系統的整體穩定，有著極為重要的價值和意義。考慮到艦船電力系統的混沌現象與陸地的電網電力結構不同，具有環境濕度大、空間容量小和電子器件集成度高的特點，本文選擇在電力系統具體工作的數學模型基礎上，動態性地對其工作中的混沌擾動現象進行針對性研究，為艦船電力系統的穩定運行、避免混沌現象的出現提供有價值的研究成果和經驗借鑒。

1電力系統裝置

1.1　電力裝置設備

艦船電力系統在正常條件下，主要依靠內部的電網系統向各個電力裝備供電，系統主要由供電裝置、傳輸裝置和負載組成，按照一定的結構方式形成一個系統整體，以提供給艦船各個用電設備使用。艦船的用電設備按照不同的設備類型可分為機械電力設備、照明電力設備、遠洋防衛設備及生活用電設備等。這些設備需要統一的供電系統的運行以保證正常的供應，無論在什么情況下，電力系統的故障都是對艦船性能的損害，所以，電力系統的穩定對艦船的使用和性能狀態的作用很大，對艦船電力系統的穩定性研究意義重大[3]。

1.2　系統的混沌現象

研究人員從電力系統的分析中發現，在電力系統運行過程中，因電子器件非線性的震蕩造成了系統的無規則性，進而引發混沌震蕩，需要采取措施和方法避免該震蕩發生。隨著艦船結構的復雜和武器裝備控制的精密，發電機組也不斷增多以維持足夠的能量，電力系統的穩定性日益重要。一旦電力系統的供應出現混沌震蕩的偏差，對艦船的性能有致命影響，所以需要根據電力系統運行的狀態參數進行分析，以避免混沌震蕩的現象出現，從機理上消除電力系統的非線性混沌現象，保障艦船電力系統的穩定性。

2艦船電力系統數學模型

2.1　發電機數學模型的建立

艦船電力系統在運行時，因系統電子器件的特性不可避免的出現非線性混沌狀態，然而這種狀態并非無法解決，隨著計算機技術的發展和現代化的系統性仿真軟件的出現，可以通過對艦船電力系統建立相應的數學模型進行技術分析，為艦船電力系統中出現的混沌現象的發生機理分析提供了可能。其結構組成如圖1所示。

圖1　系統結構圖Fig.1　System structure diagram

通過對圖1中各環節進行建模，對電力系統的運行特征、功率狀態等進行推導就可以定量地進行模型分析，在建立數學模型時，將上述結構簡化為電機系統的磁導率為恒值，電機的轉子對稱，且電機的定子繞組空間位置在方向是為互相120°，電機通風器不影響電機工作產生的電感，同時為了方便進一步的優化，系統設置2組電機系統，則圖1磁鏈結構方程如下：

電壓表示如下：

則基值為：

轉化得到的定子和轉子電壓方程分別為：

在上述方程的基礎上，電磁轉矩方程如下：

Te=ψdiq-ψqid，

則轉子方程為:

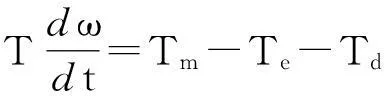
其中功角δ和功角速度ω的關系如下：

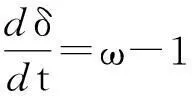
該公式即為電力系統運行的各環節數學模型。

2.2　混沌現象分析

艦船電力系統隨著艦船綜合性能的提高而逐漸復雜[4]。因此，對艦船電力系統中的低頻振蕩與混沌震蕩等非線性現象進行研究具有非常重要的實際意義。混沌現象在電力系統中的出現，具有無周期和不規則性[5]。在系統運行穩定時也有可能發生，對艦船的穩定性造成極大的危害。當系統運行中任何干擾因素且存在阻尼現象，系統的狀態為：

上式中設置在某時刻的初始條件，對該系統狀態的分析可以引入雅克比矩陣：

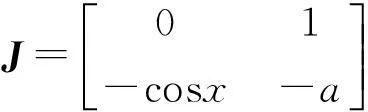
上式可根據參數的值求出系統的穩定點，如在時刻t時，參數C取值在[-4,4]區間，分別取x(1)=(arcsinc,0),x(2)=(π-arcsinc,0)。 在系統受到擾動時，穩定點在混沌分析中稱作吸引子，參數C在區間的變化相圖如圖2所示。

圖2　C變化相圖Fig.2　C phase diagram of the change

從圖2可看出，系統在吸引子附近及偏離吸引子的區域的特征有著明顯的不同，當系統取初始值(0.4,0.2)，且參數c=0.2時的時域圖曲線如圖3所示。

圖3　系統時域圖Fig.3　Time domain chart of system

由圖3可知，當系統在初始條件下，系統運行出現非線性混沌性震蕩時，由于吸引子因素的存在，系統會通過自身的調節以重新回歸正常，而保持正常的方法便是在模型狀態中設置合理的參數值，參數值確定可以根據雅克比矩陣的特征方程值來計算。因此在電力系統數學模型中，分析混沌現象并保證系統的穩定就需要選取合適的穩定點作為吸引子進行判據分析，當系統模型中選取的初始值在吸引子附近時便可保證電力系統運行處于收斂穩定的狀態。

3基于混沌分析的艦船電力系統穩定性研究

3.1　艦船電力系統的非線性模型

當對電力系統模型進行分析時，需要轉移到艦船電力系統是一個封閉的與外界不聯系的系統[6]。其運行的非線性特征可以非線性模型為基礎分析，艦船電力系統都是多機組同時維持艦船電力的供應，為簡化模型分析，現以2臺發電機組進行模型狀態分析(見圖4)。

圖4　發電機模型Fig.4　Generator model

圖中：E1∠δ1，E2∠δ2為電壓，Xd1和Xd2為電抗，R為電阻。

發電機的數學模型為

式中：Hi為轉動慣量；Di為阻尼系數。現令

則當2發電機進行并聯工作時，可推導出模型公式為：

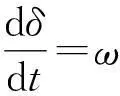
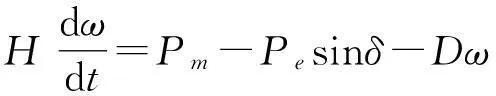
在系統運行時存在擾動，若擾動功率為：

ΔPe=ΔP·Pecos(βt)，

則模型可進一步推出：

3.2　基于混沌現象的系統穩定性研究

本文對艦船電力系統的混沌分析采用基于反演的自適應算法，根據需要合理的設計一個判別狀態特征的自適應控制器以對電力系統的狀態行為進行預判并有效控制。

3.2.1反演自適應控制法

基于反演的自適應控制法的控制器設計原理即是在原擾動狀態的非線性模型方程基礎上加上一個輸入變量u， 則擾動狀態方程變為：

α1(x)=-k1x(k1>0)，

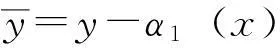
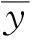
現定義李雅普諾夫函數為：

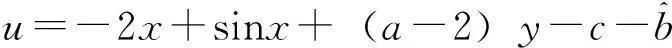
其中k>0。

在假如自適應參數控制器后，系統非線性動態模型為：

進一步轉化后：

為了保證擾動幅值參數變量b在參數估計逼近調整后系統保持在穩定狀態下，現取李雅普諾夫函數為：

則

3.2.2仿真分析

仿真分析中，為保證結果與實際運行狀態間的逼近，選取參數a=0.4，c=0.2，頻率γ=0.8，并在系統狀態出現非線性混沌震蕩時及時加入自適應控制器u，更進一步分析系統的隨后狀態特征變化。在該仿真中，取幅值擾動參數b=1.3，功角δ和功角速度ω在系統運行時的狀態如圖5和圖6所示。

圖5　功角δ的狀態曲線Fig.5　State curve of power angle δ

圖6　功角速度ω狀態曲線Fig.6　State curve of angle velocity ω

從圖5和圖6可知，當b=1.3，系統的前100s時，電力系統處于混沌狀態；在假如自適應控制器u后系統逐漸趨于穩定，艦船電力系統的非線性混沌震蕩得到很好的控制，系統運行達到了理想的狀態。該仿真實現了對系統幅值擾動參數干擾的有效處理，說明反演的自適應控制法可以在艦船電力系統中進行應用，以抑制混沌震蕩。

4結語

通過對幅值擾動對動力系統狀態影響的模型分析可以看出，頻率固定時，系統的幅值可能導致系統出現混沌現象，在利用反演算法有效引入自適應

控制器后，系統重新回歸平衡狀態。因此在艦船電力系統運行時，根據系統模型的分析可以對擾動因素選取合適的控制器參數保證系統處于穩定的運行區間，有效的避免陷入非線性的混沌狀態，保證艦船的安全和可靠。

參考文獻：

[1]徐成剛，梁世清.基于RHR算法的艦船電力系統混沌振蕩參數計算[J].艦船科學技術,2013,35(8):86-91.

XUCheng-gang,LIANGShi-qing.CompdtationofchaoticoscillationparameterinshippowersystembasedonRHRalgorithm[J].ShipScienceandTechnology,2013,35(8):86-91.

[2]賈宏杰,余貽鑫,李鵬，等.電力系統混沌現象與不同失穩模式之間的關系[J].中國電機工程學報,2003,23(2):1-4.

JIAHong-jie,YUYi-xin,LIPeng,etal.Relationshipsofpowersystemchaosandinstabilitymodes[J].ProceedingoftheCSEE,2003,23(2):1-4.

[3]張衛東, 張偉年.電力系統混沌振蕩的參數分析[J].電網技術,2000,24(12):17-20.

ZHANGWei-dong,ZHANGWei-nian.Analysisofparametersforchaoticpowersystem[J].PoulerSystemTechnology,2000,24(12):17-20.

[4]李文磊.不確定混沌電力系統的魯棒自適應跟蹤控制[J].電機控制學報，2007,11(2):170-173.

LIWen-lei.Robustadapativecontrolofchaoicpowersystenwithuncertainty[J].ElectricMachinesandControl,2007,11(2):170-173.

[5]黎古雄.基于混沌的電力系統模型研究[J].信息科學技術,2010(11):190-191.

LIGu-xiong.Researchonsystemmodelofelectricpowerbasedonchaos[J].ScienceandTechnologyInformation,2010(11):190-191.

[6]王渙文.艦船電力系統及自動裝置[M].北京:科學出版社,2004.

Research on the stability of ship power system based on chaos analysis method

MA Hong-tao

(Jiangsu Maritime Institute,Nanjing 211170,China)

Abstract：This paper build the analysis modeling about ship power system first, and according to the characteristics of nonlinear chaotic model state of power system, combined with the model amplitude perturbation parameters, we analysis of causes and influencing factors of chaos phenomenon. On the basis of this, we use of adaptive inverse algorithm of introducing an appropriate controller in the model, it can effectively avoid power system to enter into chaotic state of shock and ensure safe and stable operation of the ship and the normal of shipboard power system. The results of the study show that, shipboard power system can effectively control the stability of the state according to its characteristics, to maintain the comprehensive performance of the ship, even if the chaos phenomenon exists.

Key words：chaos analysis；power system；comprehensive performance

作者簡介：馬洪濤(1978-)，男，碩士，講師，主要研究方向為控制理論與控制工程。

收稿日期：2014-05-12； 修回日期： 2014-07-03

文章編號：1672-7649(2015)01-0152-05

doi：10.3404/j.issn.1672-7649.2015.01.032

中圖分類號：U664.14

文獻標識碼：A