無色卡爾曼濾波目標跟蹤算法的尺度參數調整*

王建宏 許 鶯 熊朝華

(信息系統工程重點實驗室 南京 210007)

?

無色卡爾曼濾波目標跟蹤算法的尺度參數調整*

王建宏 許 鶯 熊朝華

(信息系統工程重點實驗室 南京 210007)

利用無色卡爾曼濾波算法來研究目標跟蹤過程中非線性隨機系統的狀態估計問題。在無色卡爾曼濾波算法過程中,目標狀態的估計依賴于兩個設計參數——尺度參數和方差矩陣式。針對尺度參數的不同選擇將會影響整個目標狀態估計的性能質量。為此論文提出構造四種不同的最優化性能準則函數,通過對此準則函數的最小化來迭代地自適應選擇尺度參數。這四種準則函數從所使用觀測信息的不同和尺度參數優化選擇的計算復雜度來體現其各自的特性。最后通過仿真算例來驗證論文所提出的無色卡爾曼濾波目標跟蹤算法的尺度參數自適應調整策略。

目標跟蹤; 無色卡爾曼濾波; 尺度參數; 自適應調整

Class Number TP301.6

1 引言

目標跟蹤的目的是利用傳感器的觀測數據來估計目標的運動參數,包括目標的位置和速度等信息。目標跟蹤可定義為已知目標的先驗模板信息,在視頻序列中連續獲取目標運動信息(如位置、速度、尺寸等)的過程。目標跟蹤是計算機視覺領域的一項具有挑戰性的技術難點,目標跟蹤技術與目標檢測、識別技術密切相關。通常在實際工程應用中,需首先對感興趣的目標進行檢測,精確捕獲目標之后即轉化為自動跟蹤模式,在跟蹤過程中不斷對目標形態、尺度、運動規律等信息進行分析,對目標屬性進行評估、分類、識別。無論在軍事或者民用領域,目標跟蹤技術都發揮著舉足輕重的作用。

目標跟蹤算法根據算法結構的不同可分為:基于區域的目標跟蹤算法、基于特種的目標跟蹤算法、基于變形模板的目標跟蹤算法和基于貝葉斯濾波理論的目標跟蹤算法。對于基于貝葉斯濾波理論的目標跟蹤算法是將目標跟蹤問題建模成基于貝葉斯理論的最優估計問題,即將目標跟蹤過程視為已知目標狀態的先驗概率,在獲取目標新的觀測量后迭代求取目標狀態最大后驗概率的過程。

卡爾曼濾波理論是現代濾波理論建立的標志,對于系統呈現線性特性,且噪聲為高斯分布,卡爾曼濾波算法可得到系統狀態的最小均方誤差估計,該估計為最優濾波值。卡爾曼濾波算法首次在最優濾波理論中引入現代控制理論的狀態空間思想,系統的動態模型及觀測模型對應于狀態轉移方程與觀測方程,可以處理時變系統,且由于該算法是一種迭代遞推計算,易于在計算機上實現。然而卡爾曼濾波算法的約束條件過于嚴格,其要求系統必須是線性的,系統噪聲必須為參數已知的高斯噪聲。針對卡爾曼濾波算法的上述缺點,提出可應對非線性系統的無色卡爾曼濾波算法。無色卡爾曼濾波算法的核心思想是無色變換,該算法認為狀態的概率密度分布可通過能完全表達密度函數的均值和方差的有限個樣本點來描述,通過直接使用狀態或測量的非線性方程映射這些樣本點,加權求和得到更新的均值和方差。采用無色卡爾曼濾波可得到比經典卡爾曼濾波更好的濾波特性。

目標跟蹤是強調對目標狀態的融合估計與預測對被跟蹤目標進行在線建模,獲得準確的當前目標狀態,并對未來一段時域內目標狀態進行預測。本文采用無色卡爾曼濾波算法在一系列σ點處研究非線性隨機系統的狀態估計問題。因目標跟蹤的位置依賴于兩個設計參數——用來確定σ點分布的尺度參數和確定σ點選擇的方差矩陣分解。為分析尺度參數的選擇策略,提出不同自適應調整的準則函數及降低調整計算復雜度的方法。

2 系統描述

動態系統可建模成含有隱性狀態的狀態空間模型,其隱性狀態的部分信息可通過觀測量來獲取。狀態矢量可能包含有移動目標平臺的位置、速度和加速度等物理量,觀測量可采用慣性陀螺等傳感器來測取。考慮離散時間的非線性隨機系統為

(1)

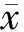
對式(1)所示的非線性隨機系統進行濾波處理的目的是要從觀測數據中推斷出若干關于狀態的估計值。在貝葉斯理論框架下,狀態估計值可在所獲取的觀測數據條件下,計算或近似狀態矢量的后驗概率分布,此分布對應觀測量下的條件概率密度函數。貝葉斯非線性濾波中的無色卡爾曼濾波算法是在狀態空間中傳播地得到一系列點,在每次時間更新步驟時都需匹配高斯分布。

目標狀態估計的設計常依賴于某個指定的性能準則函數的最小化來實現,如常見的最小均方誤差準則為

(2)

式中Zk表示直至時刻k處的所有觀測數據集,即:

Zk=[z0z1…zk]T

(3)

式(3)所示的條件均值的解析計算式通常是難以直接計算出來的,但對于其中的期望運算可采用隨機采樣算法來近似實現。若所考慮的系統為線性系統時,式(3)所示的條件期望形式的結果即為經典的卡爾曼濾波算法。而對于非線性系統,線性結構形式下未知參數的辨識需要額外的假設條件。

3 無色卡爾曼濾波算法

無色卡爾曼濾波算法遞推地計算濾波和預測過程下的均值和方差矩陣。設:

xa,b=[xaxa+1…xb]T

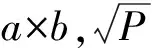
將無色卡爾曼濾波算法的具體實施過程可歸納如下:

Step 1:(初始化)設置時間瞬時刻k=0,定義先驗初始條件為預測均值和預測方差矩陣為

(4)

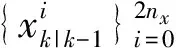
(5)

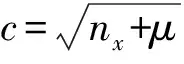
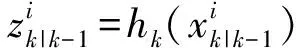
計算近似的觀測預測二階矩為

(6)

關于均值和方差矩陣的濾波估計為

(7)

其中濾波增益Kk定義為

(8)

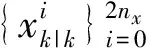
(9)

仍然在每一個σ點處,由非線性函數fk變換可得:

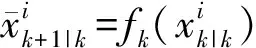
(10)

計算近似的狀態預測二階矩為

(11)

令k=k+1,繼續算法轉到Step 2。

4 尺度參數調整

尺度參數的設計依賴于包含無色變換中某些待估計量的最優化準則函數。因在無色卡爾曼濾波算法的目標狀態估計中,沒有實際真實量可獲得,對于狀態估計而言唯一可獲取的信息僅為觀測數據序列,此局限性更加強調了尺度參數的自適應調整的重要性。此節中極大似然準則和其余的另外三種準則函數都依次采用來得到尺度參數估計值。對于此四種準則函數,在無色卡爾曼濾波算法中,前兩種準則函數對應于概率密度函數形式;后四種準則函數則屬于高階矩的范疇。基于概率密度函數的準則函數的計算需要事先已知狀態和觀測噪聲的概率密度函數p(wk)和p(vk)。

1) 尺度參數極大似然準則

(12)

若預測概率密度函數p(xk|Zk-1)和觀測概率密度函數p(zk|xk)=pwk(zk-hk(xk))都為近似的高斯分布時,則有:

2) 尺度參數極大后驗概率準則

(14)

其中的后驗概率密度函數定義為

pxk|Zk(xk|Zk,μ)=p(zk|xk)p(xk|Zk-1)

×p(zk|Zk-1,μ)

(15)

3) 尺度參數最小化觀測預測誤差平方

當采用觀測預測誤差平方作為最小化的準則函數時,取觀測預測誤差平方為

(16)

對應的準則函數為

(17)

4) 尺度參數的最小化規范觀測預測誤差平方

(18)

式(17)或式(18)的優點在于規范化觀測預測誤差,此規范化過程可作用于不同的方差值,以實現觀測數據序列間的強線性相關性。

為尋找到式(12)、式(14)、式(16)和式(18)的最優化閉環解析解,可采用數值優化算法來實現此目標。通常可選擇較為成熟的數值網格法或全局自適應性。數值網格法覆蓋了一個可行的優化區域[μmin,μmax]。μ即可利用等空間網格劃分等分點來獲取。在等空間網格點處估計最優化函數,選擇取到最大化或最小化的網格點,作為首選的尺度參數估計值μ*。在全局自適應隨機搜索最大化算法中,尺度參數的最小值可設置為自適應區間的下界,即μmin=0。此值可保證無色變換后隨機變量的方差矩陣為正定形式。自適應區間的上界值可由設計者選擇,最常見的上界值μmax設置為某種概率值水平,即隨機變量x位于區域的概率。

(19)

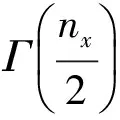
μmax=-2log(1-P*)-2

(20)

無色卡爾曼濾波目標跟蹤算法的尺度參數自適應調整過程可歸納如下,在該算法過程中采用最大化后驗概率準則形式。

Step 1:(初始化)設置μmin=0,由式(20)計算μmax,設非線性測度的門限值為T,時間瞬時刻的初始值為k=0,定義先驗初始條件的預測均值和方差矩陣分別為

Step 2:(尺度參數調整)設計尺度參數為

(21)

式(21)中λmax(zTPk|k-1z)表示矩陣zTPk|k-1z的最大特征值,采用最優化方法所得到的尺度參數值作為此步驟2中的尺度最優值。

Step 3:(濾波)實施無色卡爾曼濾波算法中的濾波步驟,并代入步驟2中的最優尺度參數估計值μk。

Step 4:(預測)實施無色卡爾曼濾波算法中的預測步驟,并代入步驟2中的最優尺度參數估計值μk。

令k=k+1,繼續算法轉到Step 2。

5 仿真算例

考慮跟蹤一個連續時間白噪聲加速度運動模型,目標的狀態定義為

(22)

即目標狀態中包含有x方向和y方向上的位置和速度,此時的維數為nx=4,構成的運動方程為

xk+1=Fxk+Gwk

(23)

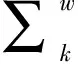
(24)

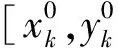
(25)

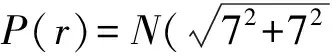
(26)

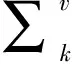
關于目標狀態估計的性能與無色卡爾曼濾波算法中的門限值間的關系見圖1所示。由圖1中而得三條曲線可知;對于較高的信噪比時,尺度參數的自適應調整并沒有帶來性能上的改善;而對于較低和中等信噪比,卻有較好的性能改善效果。

6 結語

對非線性隨機系統的目標狀態估計問題,研究無色卡爾曼濾波算法的尺度參數自適應調整策略。通過無色近似誤差來分析尺度參數,分別構造四種不同的性能準則函數,采用數值優化算法來設計尺度參數,而不是固定于某個特定的尺度參數值。為減小計算復雜度,如何僅根據觀測的局部非線性系統來設計尺度參數值是下步的研究主題。

圖1 均方誤差根與信噪比間的關系曲線

[1] 王林,王楠,朱華勇.一種面向多無人機協同感知的分布式融合估計方法[J].控制與決策,2010,25(6):814-820.

[2] 王林.多無人機協同目標跟蹤問題建模與優化技術研究[D].長沙:國防科學技術大學,2011:120-140.

[3] A. Chiuso. The role of vector autoregressive modeling in predictor based subspace identification[J]. Automatica,2007,43(6):1034-1048.

[4] Yosi B A. Distributed decision and control for cooperative UAV using ad hoc communication[J]. IEEE Transaction on Control Systems Technology,2008,16(3):511-516.

[5] Chen W H. Nonlinear disturbance observer enhanced dynamic inversion control of missiles[J]. Guidance Control and Dynamics,2003,26(1):161-166.

[6] Fabrizio Giulietti. Dynamics and control of different aircraft formation structures[J]. Aeronautical,2004,108(10):117-124.

[7] Fabrizio Giulietti. Dynamics and control issues of formation flight[J]. Aerospace Science and Technology,2005,36(9):65-71.

[8] Karimoddini A. Hybrid three dimensional formation control for unmanned helicopters[J]. Automatica,2013,49(2):424-433.

[9] Innocenti M. Management of communication failures in formation control with communication relays[J]. Journal of Aerospace Computing Information and Communication,2004,11(1):19-35.

[10] Rezaec H. Motion synchonization in unmanned aircrafts formation control with communication relays[J]. Common Nonlinear Science Number Simulate,2013,38(18):744-756.

Adaptation of Scaling Parameter for Unscented Kalman Filter Target Tracking Algorithm

WANG Jianhong XU Ying XIONG Zhaohua

(Science and Technology on Information Systems Engineering Laboratory, Nanjing 210007)

The state estimation problem of the nonlinear stochastic systems is studied by means of the unscented Kalman filter algorithm from target tracking process. In the unscented Kalman filter algorithm, the state estimation is influenced by two design parameters — the scaling parameter and a covariance matrix. Because the choice of scaling parameter may lead to the increased quality of the state estimation. So here the four different criterion functions are constructed, and the scaling parameter is chosen adaptively by minimizing one criterion function. The property of each four criterion functions is shown from their own different observed information and computation complexity. Finally, the efficiency and possibility of the adaptation of scaling parameter for unscented Kalman filter target tracking algorithm is confirmed by the simulation example results.

target tracking, unscented Kalman filter, scaling parameter, adaptation

2015年4月9日,

2015年5月27日

部委級資助項目(863計劃)(編號:2013SYAB321)資助。

王建宏,男,博士,副教授,研究方向:系統辨識。許鶯,女,碩士,研究員,研究方向:飛行控制。熊朝華,男,博士,研究員,研究方向:電子對抗。

TP301.6

10.3969/j.issn.1672-9730.2015.10.011