Phase2軟件在隧洞開挖圍巖支護時機中的應用
何 欣,曹懷園,劉永智,劉潔玉
(中國電建集團西北勘測設計研究院有限公司,西安 710065)
文章編號:1006—2610(2015)03—0049—05
Phase2軟件在隧洞開挖圍巖支護時機中的應用
何 欣,曹懷園,劉永智,劉潔玉
(中國電建集團西北勘測設計研究院有限公司,西安 710065)
新奧法支護理論允許圍巖變形,“適時”支護,能夠保證圍巖穩定的前提下,減少支護措施。文章利用phase2軟件,引入應力釋放法和彈性模量折減法解決“適時”的問題,將新奧法理論應用于德爾西水電站工程引水隧洞支護結構設計中,采用量化、清晰易懂的方式證明了合理地選擇支護時機可以優化支護結構、減少工程投資,對隧洞工程支護結構設計具有實際意義。
隧洞;支護時機;新奧法;位移;Phase2;德爾西水電站
0 前 言
地下洞室工程廣泛地應用于水利水電工程中,其中圍巖穩定問題是地下洞室最突出的工程問題。人們開始探索地下洞室的支護設計理論,早在19世紀初,學者認為只有襯砌作為受力結構,承受上部圍巖荷載,襯砌厚度設計偏大。20世紀60年代,新奧法作為新興的隧道設計方法得到關注,新奧法理論[1-2]是“合理”支護時機最初的理論基礎,最佳支護時機的確定,使我們在確保圍巖穩定和節約支護材料的工作中充滿自信。然而如何確定支護時機成為工程中的難點。
在德爾西水電站引水隧洞圍巖穩定計算中,我們應用了Phase2軟件提供的2種確定支護時機的方法,并對比其與及時支護時3種不同情況下圍巖變形和噴錨支護結構受力情況,為地下洞室開挖圍巖穩定分析提供參考和建議。
1 支護時機確定的相關理論
1.1 “允許位移量”的確定
新奧法的基本觀點:把巖體視為連續介質,根據巖體具有的黏性、彈性、塑性的物理性質,并利用洞室開挖后圍巖應力重分布而產生的變形到松動破壞有一個時間效應的動態特點,“適時”地采用薄壁柔性支護結構(以錨噴為主要手段),與圍巖緊密貼合起來共同工作,從而調動并充分利用了天然圍巖的自身承載能力,以達到洞室圍巖穩定的目的。
目前,人們正在進行各種努力以尋求一種具體量的表示方法來清楚地表達“適時”這個概念。研究發現通過圍巖“允許變形量”可以確定支護時機,但是,洞室的位移受到多種因素的影響。就某一工程而言,當地質條件、洞室形狀與尺寸、施工方法等確定時,主要受到2個因素的影響:
(1) “空間效應”,即掌子面約束作用所產生的影響。距掌子面越近,影響越大,距掌子面越遠,影響越小,到達某種距離后影響基本上可以消除。
(2) “時間效應”,通常指掌子面約束作用解除后,變形隨時間而增大的這一現象。
以上2個因素對一般巖體來說,前者占90%以上,后者占不到10%,所以人們開始探索允許釋放位移量和掌子面進尺之間的關系。 隨后經過很多學者探索,2003年,Unlu and Gercek[3]通過大量實驗提出了能準確反映圍巖塑性、而且塑性區影響的隧道位移隨開挖面(掌子面)的變化曲線——LDP曲線,公式如下:
(1)
(2)
(3)
(4)
式中:RP為隧洞中心到塑性區最外邊緣的距離,m;u0為掌子面的徑向位移,m;Rt為隧洞半徑,m;X為開挖斷面到掌子面的距離,m;umax為最大徑向位移,m。
1.2 應力釋放法和彈性模量折減法理論
巖體在開挖過程中,開挖荷載是隧洞施工期的主要荷載。實際的巖體開挖過程是開挖巖體部分的應力釋放過程,對于開挖的模擬可以簡單地假定為在邊界上施加保持圍巖單元位移不變的外力荷載的反作用力,即工程所謂的“反轉作用力”[4],亦即在開挖邊界上作用與原有支撐力相反的荷載來模擬開挖。各次開挖后地應力釋放產生的等效結點荷載為:
(5)
式中:σj為第j-1次開挖引起地應力重分布后的應力場;[Bi]為開挖單元i的幾何矩陣;a為地應力釋放系數。
根據文獻[5]的研究成果,在對隧道開挖二維模擬過程中,彈塑性力學特征參數(變形模量E、泊松比μ,內粘結力c、內摩擦角φ等)對洞室位移變化影響的靈敏度分析顯示,變形模量對位移的影響是占絕對優勢的,因而在二維仿真模擬分析過程中,將應力釋放的綜合因素可以通過變形模量的變化近似地體現出來,即彈性模量折減法。
2 分析思路
本文基本分析思路如下:
(1) 針對德爾西水電站引水隧洞Ⅲ(D)類圍巖通過式(4)計算出位移隨掌子面的變化曲線——LDP曲線,進而計算出“允許變形量”,即最佳支護時機,亦即圍巖在達到“允許變形量”之前無需支護,是通過“允許變形量”來控制支護時機;
(2) 通過應力釋放和彈性模量折減方法模擬隧洞開挖、洞周位移緩慢變形的過程,求出隨應力釋放以及彈性模量折減位移變化過程曲線,根據計算出的“允許變形量”尋找對應的應力釋放系數和折減彈性模量,此為“適時”的支護時機,即在此時,施加錨噴支護;
(3) 對比及時支護和適時支護圍巖變形和噴錨支護結構受力情況。
3 工程應用
德爾西水電站主要由首部樞紐、引水系統、發電系統和輸變電系統組成。引水系統主要建筑物包括進水口、引水隧洞、調壓井和壓力管道。引水隧洞直徑為4.1~4.9 m,全長約8 553.5 m。
引水隧洞巖體工程質量類別為Ⅱ類(A+B)、Ⅲ類(C+D)和Ⅳ類(E),本文選取具有代表性的Ⅲ(D)類圍巖進行分析。圍巖參數見表1,支護材料參數見表2。

表1 圍巖計算選取參數表

表2 支護材料力學參數表
3.1 模型建立
本文采用Phase2軟件進行計算,Phase2軟件是 Rocscience 公司開發的專門模擬地下巖體開挖工程應力及應變的二維有限元軟件,其分析步驟分3個階段,即前處理、求解和后處理。同其它有限元軟件相比,該軟件具有建模簡單、網格劃分容易和后期處理功能強大等特點,尤其在模擬地下洞室開挖時有突出優勢,可以模擬隧洞開挖及開挖后對圍巖和支護結構的影響。
由于引水隧洞布置在左岸雄厚的山體中,一般隧洞埋深100~500 m,取平均埋深為300 m,根據海姆假說[6],如果巖體是理想的塑性體,而且埋深較大,巖體就處于近似靜水壓力狀態,應力的大小等于其上覆巖體的自重,而且巖體中各個方向的應力均相等。所以,圍巖初始地應力場為σ1=σ2=σ3=γh=8MPa
模型模擬范圍取5倍洞徑,模型邊界為全約束位移邊界條件(見圖1)。模型計算采用Mohr-coulomb準則。

圖1 計算模型圖
3.2 最佳支護時機確定
(1) 應力折減法
首先采用20個計算階段進行應力折減計算,通過不同的計算階段進行應力折減,從而實現隧洞應力逐步釋放,最終得出位移隨應力釋放的變化曲線。計算模型如圖2。
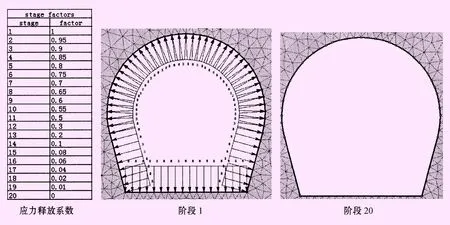
圖2 應力折減法計算模型圖
此處計算階段是人為定義的,計算階段主要是為了表示隧洞應力釋放過程。定義的計算階段越多,則應力釋放過程模擬越細致。本文定義20個計算階段來實現隧洞開挖后圍巖的應力釋放過程,其中階段1表示圍巖應力沒有釋放,即圖2中應力釋放系數為1;中間階段應力釋放系數逐漸遞減,直到最后一個階段,本文中階段20表示隧洞應力釋放完成,即圖2中應力釋放系數為0。
通過計算得知,最大位移發生在底拱,計算出底拱最大徑向位移umax=5.16 mm和隧洞中心到塑性區最外邊緣的距離RP=3.478 m,如圖3和圖4。


圖3 圍巖位移圖
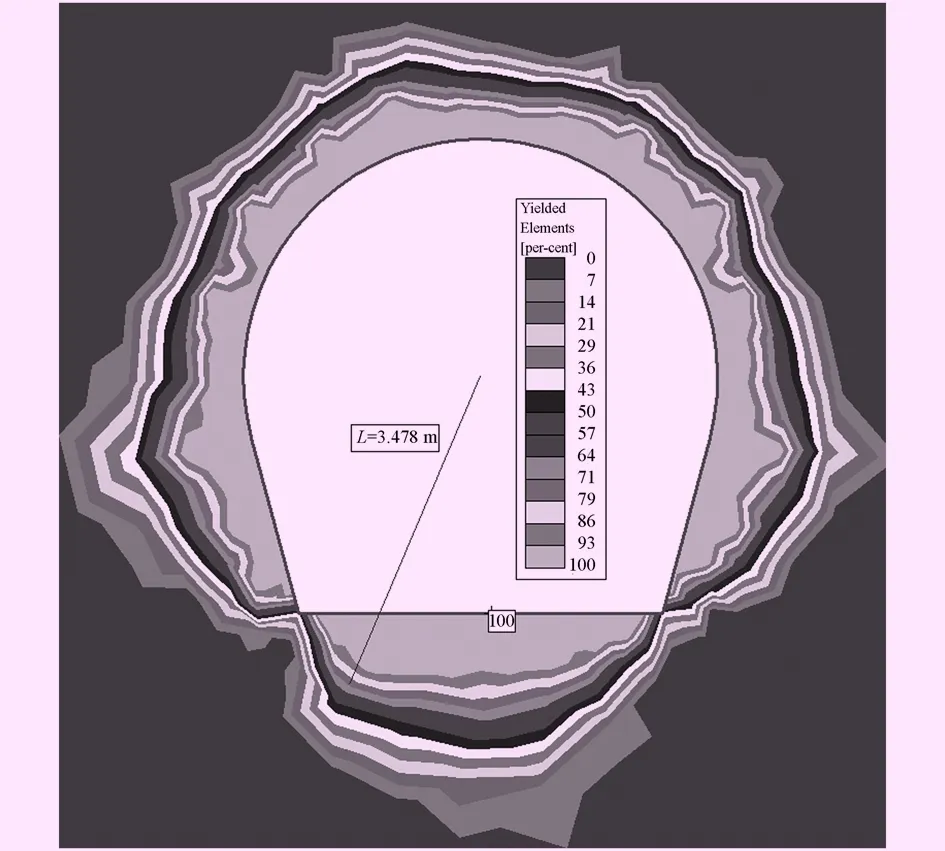
圖4 圍巖塑性區圖

圖5 LDP曲線圖
由LDP曲線可見,開挖斷面到掌子面的距離越大,隧洞變形越小,通過這一方法可評估距掌子面一定距離處洞壁位移的收斂情況、應力釋放程度及所需的支護力,借此來控制圍巖變形和支護壓力。

由底拱最大位移隨應力釋放階段變化(見圖6)可以看出,在應力釋放11~12階段之間,接近12階段,隧洞底拱徑向位移接近允許釋放位移2.72 mm,即應力折減系數取0.3~0.5時,為最佳支護時機。
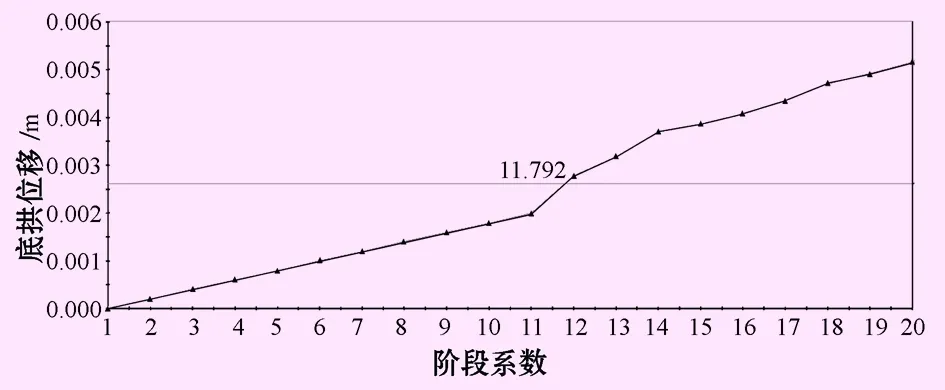
圖6 不同階段的底拱最大位移變化曲線(應力折減)
對應力折減系數進行0.3~0.5之間的細化,得出底拱最大位移隨計算階段的變化曲線,見圖7,找到最佳支護階段為14~15,應力釋放系數最終確定為0.31。

圖7 不同階段的底拱最大位移變化曲線(應力細化后)
(2) 彈性模量折減法
允許釋放位移和前面計算方法一樣,同樣可以得出允許釋放位移為2.72 mm。
上節應力折減系數為0.31,鎖定開挖部分圍巖彈性模量折減系數接近0.31,所以對彈性模量進行3 000~2 000 MPa之間的細化計算,模型如圖8。
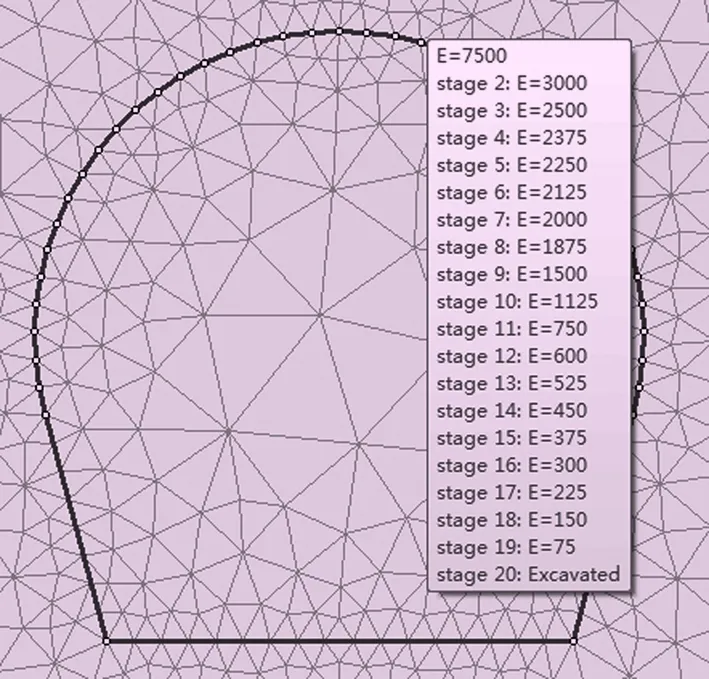
圖8 彈性模量折減模型圖
采用圖8中彈性模量折減方式,底拱最大位移隨階段變化曲線(如圖9),找到最佳支護階段為2~3,接近第3階段,最終確定開挖部分圍巖的彈性模量折減為2 600 MPa。

圖9不同階段的底拱最大位移變化曲線(彈性模量折減)
4 不同支護時機特性對比
(1) 特性對比
通過計算,分別得出應力折減法和彈性模量折減法的圍巖支護時機,與及時支護相比,圍巖的位移、塑性區分布以及支護結構的受力情況,總結如下:
1) 位移情況。開挖釋放后,洞周位移向洞內變形,且位移呈現環狀分布趨勢,從內向外逐漸減小,位移范圍在0~5 mm之間,由于頂拱是拱形,受力條件較好,同時頂拱施作錨桿支護,最大位移位于底拱,不同支護時機的底拱位移最大值見表3。
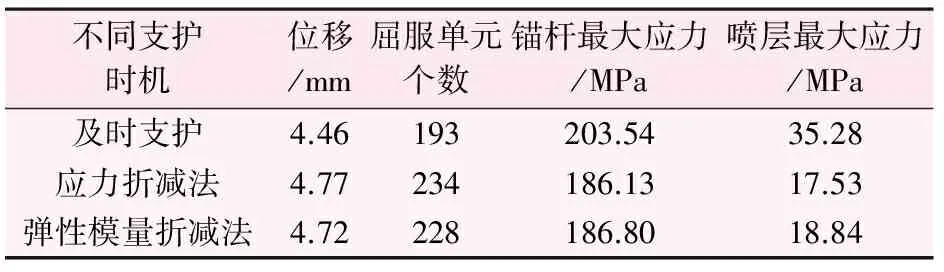
表3 不同支護時機結果對比圖表
2) 塑性區情況。開挖釋放后,洞周塑性區呈現環狀分布,但是由于頂拱是拱形,受力條件較好,同時頂拱施作錨桿支護,下部邊墻和底拱塑性區厚度大于頂拱塑性區厚度,塑性區厚度在0~0.7 m之間,不同支護時機的塑性屈服單元個數見表3。
3) 支護結構的受力情況。施作錨噴支護后,錨桿應力從洞周向外均勻遞減,錨桿受力范圍20~204 MPa,錨桿受力最大部位位于洞周頂拱;噴層軸力沿著洞周分布比較均勻,軸力范圍在0.5~3 MN之間,噴層彎矩圖分布情況為頂拱彎矩較小,邊墻下部彎矩大,彎矩范圍在-0.03~0.02 MN.m,噴層最大應力部位位于邊墻下部。不同支護時機錨桿應力和噴層應力最值見表3。
(2) 優化結論
1) 及時支護能夠及時阻止圍巖開挖后的變形和塑性區的擴展,其位移和屈服單元數相對于其他2種支護時機的較小,但是適時支護的位移和塑性區增大范圍較小,不會引起圍巖的破壞;
2) 及時支護情況下支護結構承擔了圍巖開挖后所有荷載,所以其支護結構受力明顯大于其他2種支護時機,而且噴層的受力超過了噴層的抗壓強度21 MPa,需要采用加厚噴層等支護措施;其他2種支護時機的支護結構受力較小,滿足錨桿和噴層的受力要求,因此采用適時支護可以優化支護結構;
3) 應力釋放法和彈性模量折減法的圍巖位移及支護結構受力基本相當,證明了采取任意一種方法進行合理支護時機模擬都可以達到優化支護結構的目的。
5 結 語
最佳支護時間點在工程上是節約工程材料降低工程造價的理想點,這一時刻可以保證工程材料最省和工程造價最低。本文通過德爾西水電站Ⅲ(D)類圍巖段隧洞開挖圍巖穩定性數值模擬,采用量化、清晰易懂方式向咨詢工程師解釋了引水隧洞圍巖支護時機的問題,并證明了合理地選擇支護時機可以優化支護結構,彌補了以往圍巖最佳支護時機的不確定性、不準確性和經驗性的缺點,使洞室開挖支護的優化設計和安全性評價成為可能。
[1] 韓瑞庚.地下工程新奧法[M].北京:科學出版社,1987.
[2] 劉長武.煤礦軟巖巷道的錨噴支護同新奧法的關系[J].中國礦業,2000,1(1):61-64.
[3] Hoek,E.,Carranza-Torres,C.,Diederichs,M.S.and Corkum.Integration of geothechical and structural design in tunnelling[C]//Proceedings University of Minnesota 56th Annual Geotechnial Engineering Conference.Minneapoils,29 February 2008,1-53.
[4] 王偉.獅子坪水電站不良地質隧洞開挖方式與支護參數優化研究[D].武漢:武漢理工大學,2007.
[5] 陳方方.地下洞室彈塑性仿真反分析研究[D].西安:西安理工大學,2004.
[6] 王樹洪.高地應力高外水壓隧洞圍巖穩定和支護結構研究及應用[D].南京:河海大學,2004.
[7] R. K. Goel,Bhawani Singh, Rock mass classification[M].ELsevier Science Ltd., 1999.
Application of Phase 2 Software in Support Time of Surrounding Rock in Tunneling
HE Xin, CAO Huai-yuan, LIU Yong-zhi, LIU Jie-yu
(POWERCHINA Xibei Engineering Corporation Limited, Xi'an 710065,China)
New Austrian tunneling method allows deformation of surrounding rock, support is provided at Proper Time. Under the precondition of securing stability of surrounding rock, support measures is decreased. In this paper, Proper Time is determined by application of stress release method and elastic module reduction method through Phase 2 software. Accordingly, theory of new Austrian tunneling method is applied in design of support structure of the headrace tunnel of Delsi Hydropower Project. By application of quantitive, clear and simple means, it verifies that the proper support time allows to optimize support structure and reduce investment as well. This is practical for the design of support structure of tunneling works.
tunnel; support time; new Austrian tunneling method (NATM); displacement; Phase 2; Delsi Hydropower Project
2015-04-15
何欣(1987- ),女,陜西省戶縣人,助理工程師,主要從事水工和巖土設計工作.
TV222.2;TV554
A
10.3969/j.issn.1006-2610.2015.03.014

