陶瓷材料維氏壓痕形貌仿真與實驗分析

王家梁，馬德軍，陳 偉，黃 勇，白盟亮

(1裝甲兵工程學院 機械工程系，北京 100072； 2總裝備部 西安軍事代表局，西安 710065)

?

陶瓷材料維氏壓痕形貌仿真與實驗分析

王家梁1，馬德軍1，陳 偉1，黃 勇1，白盟亮2

(1裝甲兵工程學院 機械工程系，北京 100072； 2總裝備部 西安軍事代表局，西安 710065)

基于有限元數值分析模型對陶瓷材料維氏壓入過程中產生的壓痕形貌進行仿真。以Si3N4和ZrO2兩種典型陶瓷材料為例，對其有限元仿真壓痕與實驗測量壓痕的對角線半長和維氏硬度進行對比，結果表明，Si3N4和ZrO2的有限元仿真壓痕與實驗測量壓痕對角線半長分別相差0.39%和-0.53%，維氏硬度分別相差-2.7%和4.2%。隨著壓頭與材料間的摩擦因數由0變化至0.5，有限元仿真壓痕與實驗測量壓痕的對角線半長分別相差0.28%和0.27%，維氏硬度分別相差0.14%和0.21%。此外，應用本方法對其他幾種典型陶瓷材料(Al2O3,ZTA,SiC,Silica)維氏壓入有限元仿真計算值與實驗真實測量值進行了對比，其壓痕對角線半長分別相差1.14%,-0.57%,-0.89%,0.41%，維氏硬度分別相差-2.24%,1.12%,1.85%,-0.86%。據此可知，陶瓷材料維氏壓痕形貌可由有限元數值仿真方法獲得，從而解決了陶瓷材料維氏硬度測試過程中因壓痕不夠清晰導致的測量數據不準問題，為下一步探索基于儀器化壓入響應識別陶瓷材料維氏硬度以及其他各力學性能參數提供技術基礎。

陶瓷材料；有限元仿真；壓痕對角線半長；維氏硬度；摩擦因數

維氏硬度測試作為一種快速檢測材料力學性能的簡便方法，其值能夠一定程度上反映出材料的彈塑性性能[1-5]，一直以來受到國內外研究學者的廣泛關注[6-10]。特別是對于陶瓷材料，斷裂韌性作為衡量陶瓷脆性或韌性的重要力學性能指標，其值的準確測量一直以來是國內外研究人員普遍關注的熱點和難點。然而，傳統壓痕法測試陶瓷材料斷裂韌性的諸多公式中(Evans公式[11]、Lawn公式[12]、Anstis公式[13]、Niihara公式[14]、JISR1607—1990公式[15])，普遍需要對維氏壓痕對角線半長及維氏硬度進行準確測量，由于肉眼對壓痕形貌進行觀測不可避免的會對測試結果引入因人為因素導致的誤差，特別是對壓痕形貌識別較困難的材料而言(如熔融硅材料，壓痕形貌如圖1所示)，測量結果往往誤差較大。

為此，本工作以Si3N4和ZrO2兩種典型陶瓷材料為例，基于有限元數值分析模型對兩種材料維氏壓痕形貌進行仿真，并與壓痕實驗測量結果進行比較。從而驗證陶瓷材料維氏壓痕形貌仿真方法的有效性，解決陶瓷材料維氏硬度測試過程中因壓痕不夠清晰導致的測量數據不準問題，為下一步探索基于儀器化壓入響應識別陶瓷材料維氏硬度以及其他各力學性能參數提供技術基礎。

圖1 熔融硅維氏壓痕形貌Fig.1 Vickers impression morphology of fused silica

1 維氏壓入壓痕形貌仿真

標準的四棱錐Vickers壓頭面角為136°，其對Si3N4和ZrO2兩種陶瓷材料進行的維氏壓入產生的壓痕形貌如圖2所示。

圖2 兩種陶瓷材料維氏壓入壓痕形貌 (a)Si3N4壓痕形貌；(b)ZrO2壓痕形貌Fig.2 Vickers indentation impression morphology of two kinds of ceramic materials (a)impression morphology of Si3N4;(b)impression morphology of ZrO2

應用商用有限元軟件Abaqus[16]建立維氏壓入三維有限元模型，為降低計算成本，根據模型對稱性可以取Vickers壓頭的八分之一建立模型進行分析(如圖3所示)，被壓材料也定義為與壓頭對稱性相符的八分之一模型。

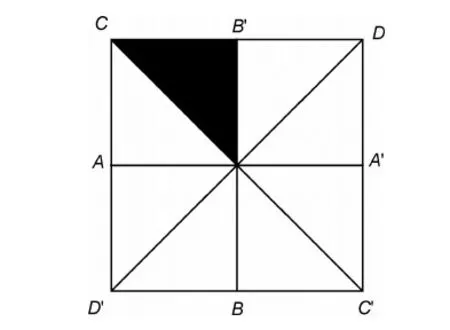
圖3 Vickers壓頭建模示意圖Fig.3 Schematic diagram of Vickers indenter modeling

對于有限元模型的網格劃分，靠近壓頭尖端的局部網格劃分精細，遠離壓頭的區域劃分較為稀疏。考慮到本工作建立的有限元模型主要針對壓痕對角線進行計算，特別對被壓材料的壓痕對角線區域網格進行精細劃分，如圖4所示。通過網格收斂性分析和遠場無關性分析，最終確定壓頭和被壓材料共劃分215382個四面體單元和54720個六面體單元。根據儀器化壓入方法[17,18]獲得的Si3N4和ZrO2兩種陶瓷材料的彈塑性參數作為有限元數值仿真的材料屬性進行輸入，其中Si3N4的彈性模量E=304GPa，泊松比為v=0.2，屈服強度σy=7800MPa，硬化指數n=0；ZrO2的彈性模量E=228GPa，泊松比為v=0.2，屈服強度σy=5700MPa，硬化指數n=0。金剛石Vickers壓頭定義為彈性體，其中彈性模量E=1141GPa，泊松比v=0.07。壓頭和被壓材料的接觸摩擦因數分別取f=0，0.15，0.3，0.5。整個陶瓷材料維氏壓入仿真計算采用非線性大變形理論。

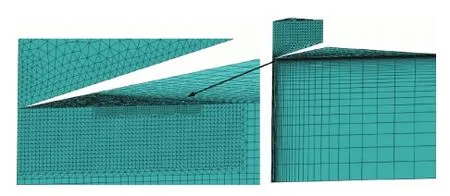
圖4 陶瓷材料維氏壓入三維有限元模型圖Fig.4 3D finite element model of Vickers indentation in ceramic materials

對于壓痕對角線半長的仿真結果識別，關鍵在于確定壓頭卸載、材料回彈完全恢復后的壓痕邊緣有限元節點位置，該位置必然為各節點連線的曲率最大點。因此，本工作確定壓痕邊緣有限元節點位置主要分為兩步：第一步，當壓頭以最大壓入載荷Pm壓入陶瓷材料至最大壓入深度hm時，確定出此時八分之一模型沿壓痕對角線方向的對稱面處壓頭與被壓材料表面的接觸節點A(此節點位置可由接觸應力值確定)，如圖5所示；第二步，當壓頭完全卸載后，識別接觸節點A的位置坐標，從而得到壓痕對角線半長的有限元數值仿真結果。

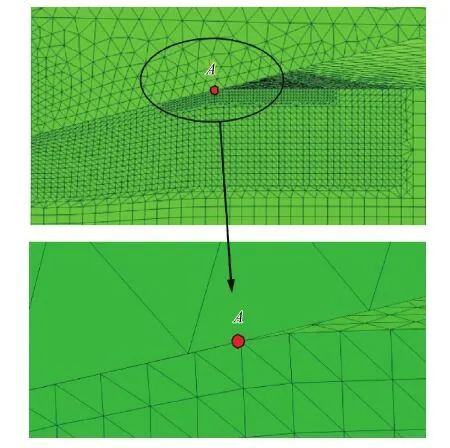
圖5 最大壓入深度對應的沿壓痕對角線方向壓頭與 被壓材料接觸節點(A)位置示意圖Fig.5 Schematic diagram of the maximum contact node position(A) between indenter and material of impression along the diagonal direction corresponding to the maximum indentation depth

基于上述有限元數值仿真方法，對兩種陶瓷材料進行維氏壓痕形貌的有限元數值仿真，固定壓頭最大壓入深度hm=5μm，針對不同接觸面摩擦因數對應的兩種陶瓷材料維氏壓痕對角線半長a和維氏硬度HV的仿真計算值如表1,2所示。

由表1，2可以看出，不同接觸面摩擦因數(f=0，0.15，0.3，0.5)對兩種陶瓷材料壓痕對角線半長和 維氏硬度的影響極小，其中，Si3N4和ZrO2的壓痕對角線半長差別分別為0.28%和0.27%，維氏硬度差別分別為0.14%和0.21%。由此可知，本工作所采用的有限元數值仿真方法對陶瓷材料壓痕對角線半長和維氏硬度的識別不受接觸摩擦因數的影響，具有一定的可靠性，從而有望解決陶瓷材料維氏硬度測試過程中因壓痕不夠清晰導致的測量數據不準問題。

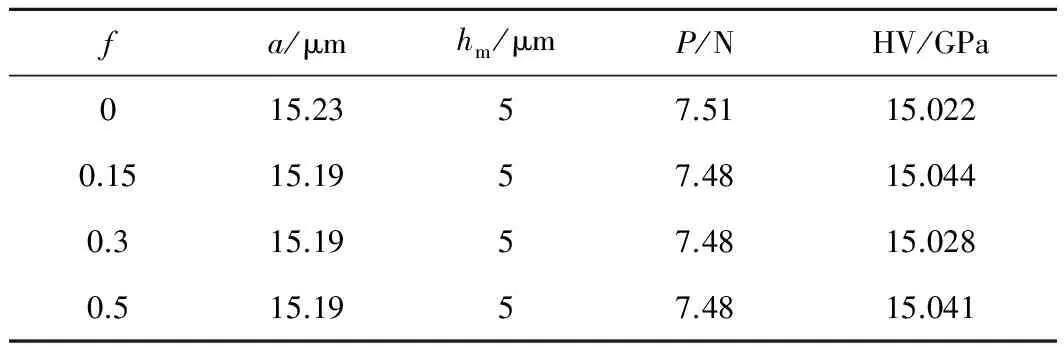
表1 不同接觸面摩擦因數對應的Si3N4材料維氏壓痕對 角線半長和維氏硬度有限元仿真結果

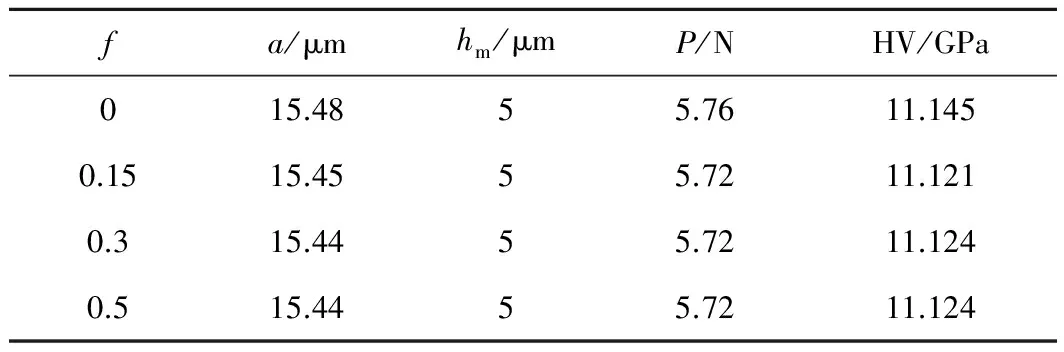
表2 不同接觸面摩擦因數對應的ZrO2材料維氏壓痕對角線半長和維氏硬度有限元仿真結果

2 維氏壓入實驗

按照國家標準GB/T 21838.1—2008[19]的要求委托中國建筑材料科學研究總院陶瓷科學研究院制備Si3N4和ZrO2兩種陶瓷材料的壓入標準試樣塊。其中，Si3N4和ZrO2試樣均采用高純(原料純度≥99.9%)超細粉料通過等靜壓成型方法制得，其試樣致密度分別大于99%和98%，密度分別為3.21g/cm3和6.02g/cm3。采用自主研制的具有完全自主知識產權的高精度宏觀儀器化壓入儀[20]對兩種材料進行維氏壓入實驗，所用四棱錐Vickers壓頭的面角已經過標定。加載階段的加載速率為0.5N/s，在保證壓痕形貌能夠準確識別的情況下，本實驗取最大壓入載荷為100N；保載30s；卸載階段的卸載速率與加載速率保持一致，為0.5N/s。按照上述壓入要求，重復實驗10次，壓痕之間保持適當距離，避免實驗結果相互干擾。利用光學顯微鏡，對兩種陶瓷材料維氏壓入實驗獲得的壓痕形貌進行觀測，各壓痕參數量取數據分別見表3，4所示。

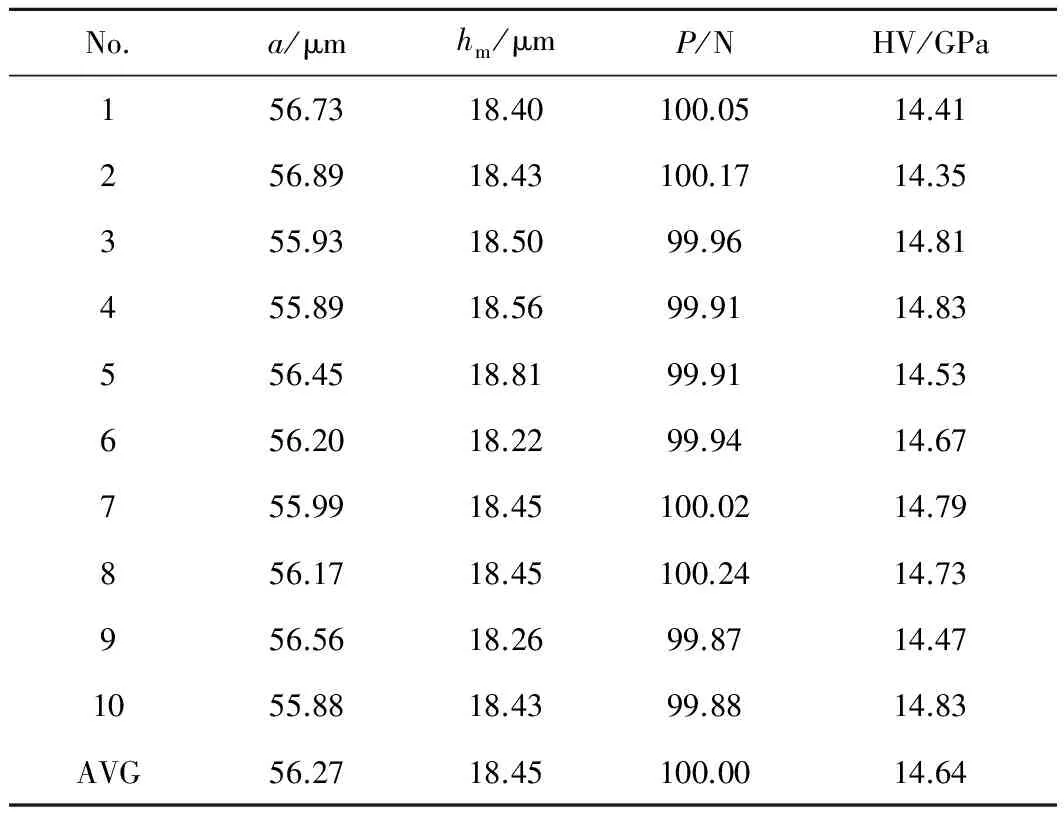
表3 Si3N4材料維氏壓入實驗獲得的壓痕對角線半長和維氏硬度測量值

3 結果分析

由于維氏壓入過程中，Si3N4和ZrO2兩種陶瓷材料與金剛石壓頭的實際接觸摩擦因數f難以確定，且考慮到前文所述摩擦因數對壓痕對角線半長的影響極小，本研究取接觸面摩擦因數f=0.15對應的兩種陶瓷材料維氏壓入有限元仿真獲得的壓痕對角線半長和維氏硬度與實驗真實測量值進行對比，結果分別見表5，6所示。其中，a，hm，HV分別為有限元仿真獲得的壓痕對角線半長、最大壓入深度和維氏硬度，a′，hm′，HV′分別為實驗所測真實壓痕對角線半長、最大壓入深度和維氏硬度。

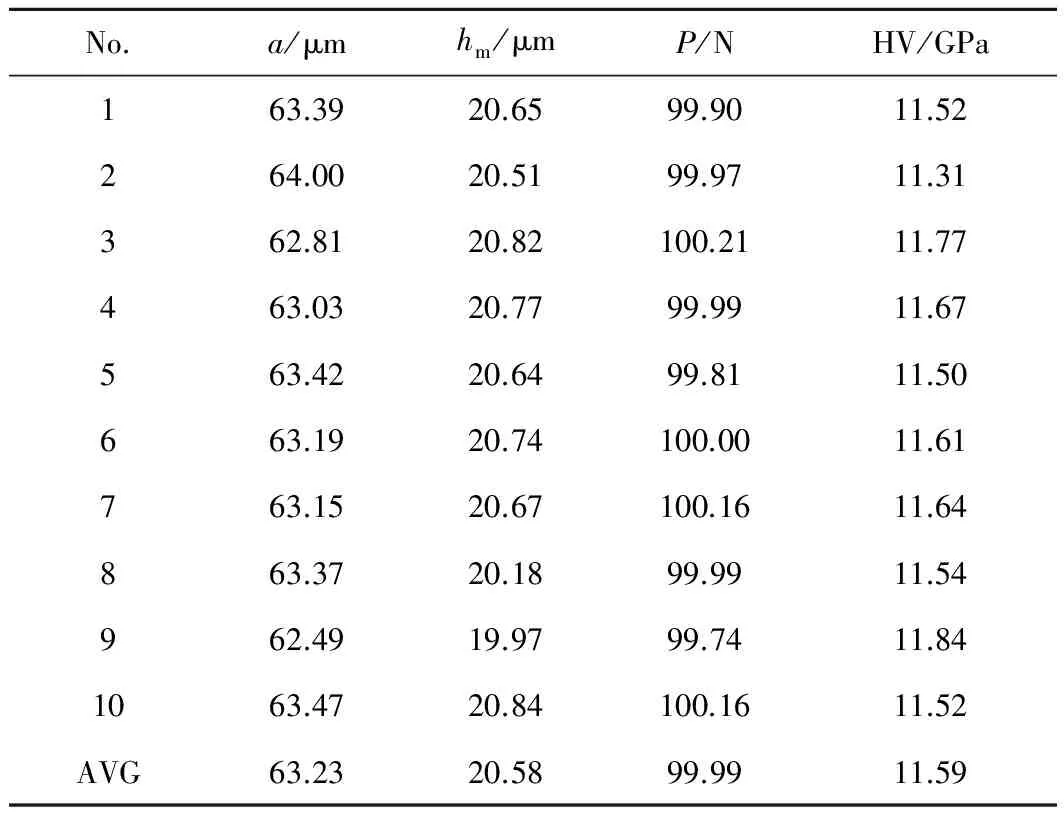
表4 ZrO2材料維氏壓入實驗獲得的壓痕對角線半長和維氏硬度測量值

由表5，6可知，本工作所采用的有限元仿真方法識別的Si3N4和ZrO2壓痕對角線半長與實驗真實測量值分別相差0.39%和-0.53%，維氏硬度分別相差-2.7%和4.2%。鑒于兩種材料的壓痕仿真識別結果與真實測量值偏差較小，且維氏硬度偏差值與維氏硬度測量最大允許誤差(±2%)[21]相當，從而說明利用有限元數值方法對陶瓷材料壓痕形貌的仿真計算具有一定的可靠性。

表7是應用本方法對其他幾種典型陶瓷材料維氏壓入有限元仿真計算值與實驗真實測量值的對比結果。其中，Al2O3(原料純度≥99.99%) 、ZTA(原料純度≥99.99%的25%ZrO2和75%的Al2O3)和SiC(原料純度≥98%)由中國建筑材料科學研究總院陶瓷科學研究院提供，其密度分別為3.95，4.28，3.10g/cm3，Silica試樣是由寶山鋼鐵股份有限公司提供的納米壓入儀用標準樣品(國標編號：GSB03-2496—2008)，原料純度≥99.9%，密度為2.20 g/cm3。在保證壓痕形貌能夠準確識別的情況下，本實驗分別取Al2O3，ZTA，SiC，Silica的最大壓入載荷為100，100，100，0.25N。

表5 Si3N4材料維氏壓入有限元仿真計算值與實驗真實測量值對比數據

表6 ZrO2材料維氏壓入有限元仿真計算值與實驗真實測量值對比數據

表7 幾種典型陶瓷材料維氏壓入有限元仿真計算值與實驗真實測量值對比數據[17，18]

由表7中數據可知，Al2O3，ZTA，SiC，Silica的仿真最大壓入深度hm分別為17.70，16.80，18.92，1.50μm時，仿真壓痕對角線半長與實驗真實測量值分別相差1.14%，-0.57%，-0.89%，0.41%，維氏硬度分別相差-2.24%，1.12%，1.85%，-0.86%。據此充分說明本方法對不同彈性模量、不同硬度的陶瓷材料均具有一定的有效性。

4 結論

(1)有限元數值方法對陶瓷材料壓痕對角線半長和維氏硬度的識別不受接觸摩擦因數的影響。隨著壓頭與材料間的摩擦因數由0變化至0.5，有限元仿真壓痕與實驗測量壓痕的對角線半長差別分別為0.28%和0.27%，維氏硬度差別分別為0.14%和0.21%。

(2)應用本方法所測材料的壓痕仿真識別結果與真實測量值偏差較小。其中，Si3N4和ZrO2的有限元仿真壓痕與實驗測量壓痕對角線半長差別分別為0.39%和-0.53%，維氏硬度差別分別為-2.7%和4.2%。其他幾種典型陶瓷材料(Al2O3，ZTA，SiC，Silica)維氏壓入有限元仿真計算值與實驗真實測量值進行了對比，其壓痕對角線半長分別相差1.14%，-0.57%，-0.89%，0.41%，維氏硬度分別相差-2.24%，1.12%，1.85%，-0.86%。從而說明利用有限元數值方法對陶瓷材料壓痕形貌的仿真計算具有一定的可靠性。

(3)陶瓷材料維氏壓痕形貌仿真方法對解決陶瓷材料維氏硬度測試過程中因壓痕不夠清晰導致的測量數據不準問題具有一定的可行性，為下一步探索基于儀器化壓入響應識別陶瓷材料維氏硬度以及其他各力學性能參數提供技術基礎。

[1] TABOR D. The Hardness of Metals[M].Oxford: Clarendon Press,1952.

[2] OLIVER W C, PHARR G M. An improved technique for determining hardness and elastic modulus using load and displacement sensing indentation experiments[J]. J Mater Res, 1992, 7(6):1564-1583

[3] CHANG Y T, CHANG C M. Relationship between hardness, elastic modulus and the work of indentation[J]. Appl Phys Lett,1998, 73(5):614-616.

[4] FAN G J, JIANG W H, LIU F X, et al. The effects of tensile plastic deformation on the hardness and Young’s modulus of a bulk nanocrystalline alloy studied by nanoindentation[J]. J Mater Res, 2007, 22(5):1235-1239.

[5] SUN Y, WANG Q M. Analysis of the elastic-plastic indentation properties of materials with varying ratio of hardness to Young’s modulus[J].Acad J XJTU,2008, 20(3):178-182.

[6] KENJI S, TSUYOSHI H, TAKAYUKI K. Elastic properties and Vickers hardness of optically transparent glass-ceramics with fresnoite Ba2TiSi2O8nanocrystals[J]. Mater Res Bull, 2011, 46(6):922-928.

[7] GONG J H, WU J J,GUANG Z D. Examination of the indentation size effect in low-load Vickers hardness testing of ceramics[J]. J Eur Ceram Soc,1999, 19(15):2625-2631.

[8] SEUNG K K, JU Y K, CHAN P P, et al. Conventional Vickers and true instrumented indentation hardness determined by instrumented indentation tests[J]. J Mater Res, 2010, 25(2):337-343.

[9] SHABDAD S A, McCABE J F M, BULL S, et al. Hardness measured with traditional Vickers and Martens hardness methods[J]. Dent Mater,2007, 23(9):1079-1085.

[10] PAN X F, ZHANG H,ZHANG Z F, et al. Vickers hardness and compressive properties of bulk metallic glasses and nanostructure-dendrite composites[J]. J Mater Res,2005, 20(10):2632-2638.

[11] EVANS A G, CHARLES E A. Fracture toughness determination by indentation[J]. J Am Ceram Soc, 1976, 59(7-8): 371-376.

[12] LAWN B R, EVANS A G, MARSHALL D B. Elastic/plastic indentation damage in ceramics: the median/radial crack system[J]. J Am Ceram Soc, 1980, 63(9-10): 574-581.

[13] ANSTIS G R, CHANTIKUL P, LAWN B R, et al. A critical evaluation of indentation techniques for measuring fracture toughness I：direct crack measurements[J]. J Am Ceram Soc, 1981,64(9): 533-538.

[14] NIIHARA K, MORENA R HASSELMAN D P H. Evaluation ofKICof brittle solids by the indentation method with low crack-to-indent ratios[J]. J Mater Sci Lett, 1982,l(1): 13-16.

[15] Minister of International Trade and Industry. JISR1607—1995. Testing Methods for Fracture Toughness of High Performance Ceramics[S]. Tokyo: Japanese Standards Association,1990.

[16] ABAQUS 6.10/CAE User’s Manual[Z]. Dassault Systems Simulia Corp Providence, RI,USA, 2010.

[17] 馬德軍.材料力學性能儀器化壓入測試原理[M].北京:國防工業出版社,2010.

[18] 郭俊宏.材料彈塑性參數儀器化壓入識別方法與測試技術研究[D].北京:裝甲兵工程學院, 2013.

[19] 中國鋼鐵工業協會.GB/T 21838.1—2008金屬材料硬度和材料參數的儀器化壓痕試驗第1部分:試驗方法[S]. 北京:中國標準出版社,2008.

[20] 馬德軍,宋仲康,郭俊宏,等.一種高精度壓入儀及金剛石壓頭壓入試樣深度的計算方法[P].CN Patent: CN102288500A, 2011-12-21.

[21] 國家冶金工業局.GB/T 4340.2—1999金屬維氏硬度試驗第2部分:硬度計的檢驗[S].北京:中國標準出版社,1999.

Simulation and Experimental Analysis on Vickers Indentation Morphology of Ceramic Materials

WANG Jia-liang1,MA De-jun1,CHEN Wei1,HUANG Yong1,BAI Meng-liang2

(1 Department of Mechanical Engineering,Academy of Armored Force Engineering,Beijing 100072,China;2 Xi’an Military Representatives Bureau, the General Armaments Department,Xi’an 710065,China)

The indentation morphology of ceramic materials caused by the Vickers indentation process was simulated based on the finite element analysis model. Take two kinds of ceramic materials (Si3N4and ZrO2) for example, the indentation diagonal half-length and the Vickers hardness from finite element simulation and that from the experimental measurement were compared. The results show that the difference between Si3N4and ZrO2in indentation diagonal half-length from finite element simulation and experimental measurement is 0.39% and -0.53% respectively, the difference in Vickers hardness is -2.7% and 4.2%. With the friction coefficient between the indenter and the material changes from 0 to 0.5, the difference in indentation diagonal half-length from finite element simulation and experimental measurement is 0.28% and 0.27%, the difference in Vickers hardness is 0.14% and 0.21%. In addition, apply this method to compare the Vickers indentation finite element simulation values of other typical ceramics materials (Al2O3,ZTA,SiC and Silica) with the experimental measurement values, the difference of indentation diagonal half-length is 1.14%, -0.57%, -0.89% and 0.41% respectively, the difference in Vickers hardness is -2.24%, 1.12%, 1.85% and -0.86% respectively. It can be seen that the Vickers indentation morphology of ceramic materials can be derived by the finite element numerical simulation method, thereby this method can solve the problem of indentation measurement data inaccuracies, which caused by unclear indentation in the process of indentation method to measuring the Vickers hardness of ceramic materials. This method provides the technical foundation for further exploration based on the response of instrumented indentation to identify the Vickers hardness and any other mechanical properties of the ceramic materials.

ceramic material;finite element simulation;indentation diagonal half-length;Vickers hardness;friction coefficient

10.11868/j.issn.1001-4381.2015.11.012

TQ174.75

A

1001-4381(2015)11-0071-06

2014-07-30；

2015-04-30

王家梁(1986—)，男，博士研究生，主要從事材料力學性能測試方法研究，聯系地址：北京市豐臺區長辛店杜家坎21號裝甲兵工程學院機械工程系(100072)，E-mail:wjllongman@126.com