基于混合人工魚群優化SVR的交通流量預測

姚衛紅，方仁孝，張旭東

（大連理工大學 計算機科學與技術學院，遼寧 大連 116024）

0 引 言

準確、可靠的道路交通流量信息是智能交通系統中交通控制和信息管理的重要組成部分.在每天的車輛出行高峰時段，不準確的交通流量信息會增加出行者時間，造成道路擁堵、能源消耗和環境污染，所以高峰時段準確的交通流量預測就顯得尤為重要［1－3］.

傳統的交通流量預測模型有基于數學測定方法的自回歸移動平均方法（ARIMA）模型、卡爾曼濾波模型和非線性回歸模型［4］.這些模型有計算簡單、速度快的優點，但是它們不能處理交通流量信息的不確定性和非線性的復雜特征.目前常用的交通流量預測模型有基于知識發現的智能模型，如模糊理論、小波理論和ANN 人工神經網絡［5］.ANN 模型由于其無先驗性地解決高復雜度問題的良好性能在交通流量預測領域取得了一定的成果.但ANN 是基于經驗風險最小化的，存在收斂速度慢和訓練誤差非凸的問題，難以求得最優解［3］.

支持向量機（SVM）最早是為了解決模式識別和分類問題的，隨著Vapnik的ε不敏感損失函數的引入，SVM 開始用于解決非線性回歸估值問題，稱之為支持向量回歸（SVR）.SVR 能很好地解決小樣本、非線性和高維的問題，已經成功地用于交通系統領域的預測［2－3］.然而，SVR 模型不能得到準確的預測結果是因為SVR 模型中參數組合C、ε和σ的值設置得不準確.傳統的人工選擇和網格遍歷的方法存在主觀經驗判斷和尋優時間長的缺點，并不能得到好的效果，但是運用智能的選擇進化算法（如ACO、PSO 和AFS 等）優化SVR參數能選擇到合適的回歸參數［6－7］.每 種 智能進化算法都有各自的優缺點.研究表明，采用混合優化算法比采用單一優化算法能取得更好的預測結果［8－9］.

本文針對AFS算法的初始參數設置較多和步長因子的設置對尋優性能的影響的缺點，提出采用PSO 算法公式改進AFS算法，減小步長因子對AFS算法的影響，并且引入混沌機制初始化魚群位置，來進行SVR 的參數選擇，建立混沌粒子群人工魚群混合優化SVR 的CPSOAFS－SVR交通流量預測模型.

1 SVR 模型

SVR 的核心思想是基于結構風險最小化原則，通過定義一個非線性映射將輸入數據集映射到高維特征空間，在這個高維特征空間存在一個線性函數f能夠明確地表示輸入數據集和輸出數據集之間的非線性關系.SVR 函數定義如下：

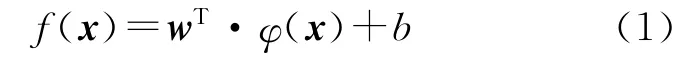
式中：f決定預測值，φ（·）為映射函數，x為輸入數據向量，w和b分別為高維特征空間中的向量和常數，兩者的值可以通過下式求得：

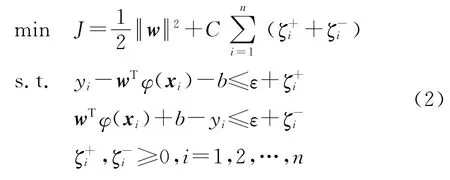
式中：C為懲罰系數，ε為不敏感損失函數的最大誤差系數，ζ＋i和ζ－i為松弛系數，n為輸入數據的樣本個數.SVR 致力于求解高維特征空間的最優超平面，使得輸入輸出數據集之間的整體誤差最小.

通過求解上述帶不等式約束的二次優化問題，可以得到式（1）中的參數向量w的值：

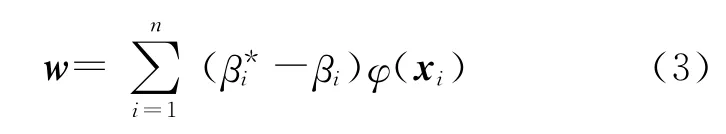
其中β＊i和βi分別為運用拉格朗日乘子法求解二次優化問題的拉格朗日系數.最后SVR 問題就得到如下方程：

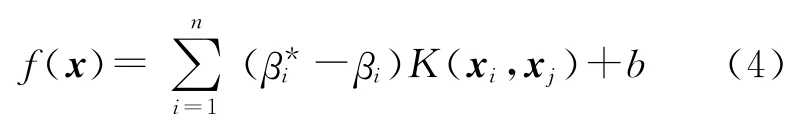
其中K（·）為計算高維特征空間中的兩個輸入向量內積的核函數.本文采用Gauss函數K（xi，xj）＝exp（－xi－xj2／2σ2）作為模型的核函數.

SVR 模型中參數組合C、ε和σ的值的選擇影響預測的精度，所以建立優化的交通流量預測模型就需要選取最優的參數組合來最小化實際值和預測值之間的誤差［7］.

2 CPSOAFS－SVR 預測模型

2.1 AFS算法

人工魚群（AFS）算法是由李曉磊于2003年提出的通過模擬自然界中魚群的行為得到的一種群智能優化算法［10］.每條人工魚代表D維空間中的一個點xi，人工魚個體所在位置的適應度為Fi，本文的交通流量預測致力于Fi最小化.兩條人工魚之間的距離為xi－xj，其他的參數包含魚群個數n、視野v、步長s和擁擠度δ.每條人工魚通過模擬魚的覓食、聚群、追尾和隨機行為尋找最優適應度來進行搜索優化過程.

（1）覓食行為

覓食行為是人工魚趨向較優適應度的基本行為.其計算公式為

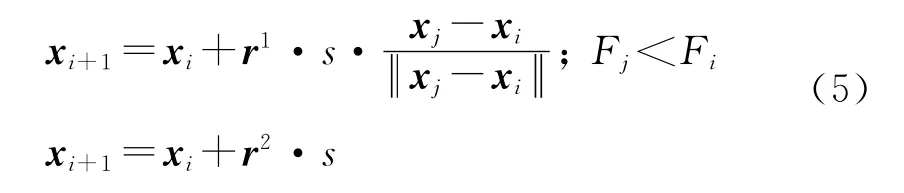
式中：r1和r2分別代表隨機變量區間［0，1］和［－1，1］，xi代表第i條人工魚位置信息，Fj為xi在視野范圍內隨機移動到另一位置xj的適應度.若反復嘗試若干次后，仍不滿足前進條件，則隨機移動一步.

（2）聚群行為

聚群行為是人工魚個體在游動過程中為了趨利避害，自然地聚集成群向鄰居中心移動的行為.其計算公式為

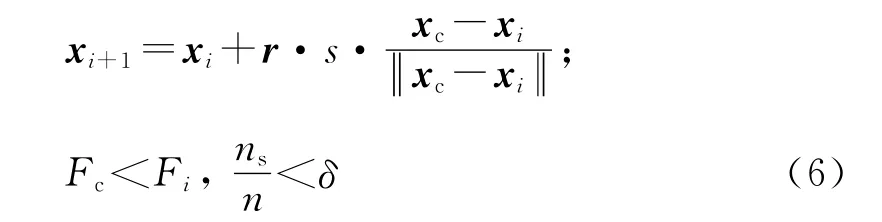
其中ns為當前視野范圍內的鄰居數目，xc代表所有鄰居的聚集群體的中心位置.當xc的適應度優于當前xi位置的適應度，并且魚群不太擁擠時，xi就向中心位置移動.否則，執行覓食行為.

（3）追尾行為

追尾行為是一種向著附近的有更優適應度的人工魚移動的行為.其計算公式為

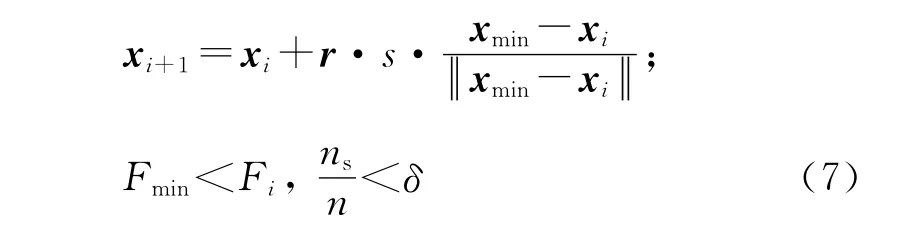
其中xmin代表視野范圍內的最優適應度的人工魚所在位置.當xmin的適應度優于當前xi位置的適應度，并且魚群不太擁擠時，xi就向最優適應度位置移動.否則，執行覓食行為.

另外，AFS算法設置了公告牌來記錄最優狀態和當前迭代的最優人工魚位置信息.

2.2 PSO 算法

PSO 算法是一種廣泛用于解決數值優化問題的群智能優化算法.PSO 算法假設解空間內的每個位置為一個粒子，每個粒子具有由被優化函數確定的適應度，同時每個粒子按照一定的搜索規則和較優適應度方向對自身的速度及位置進行調整來求得最優解.PSO 算法的速度和位置更新公式為

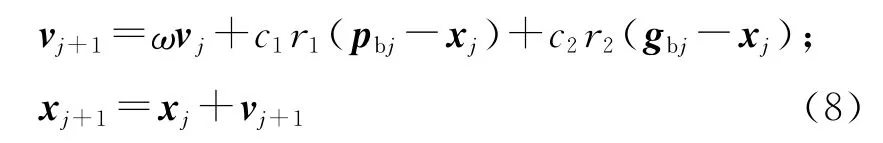
式中：vj為粒子當前速度，vj＋1為更新后的粒子速度，ω為 速 度 慣 性 權 重，c1和c2為 加 速 系 數，r1和r2為區間（0，1）內的隨機數，xj和xj＋1分別為粒子的當前位置和更新后的位置，pbj為粒子當前自身最優位置，gbj為粒子當前全局最優位置.

2.3 PSO 算法公式改進AFS算法

AFS算法初始參數的設置對算法性能有一定的影響.AFS算法的步長因子限制了人工魚個體的移動步長，如果步長太小就將個體魚限制在較小搜索空間，增大了尋優時間；如果步長太大，則可能找不到最優值.并且步長因子依賴于人工魚之間距離的計算，對算法性能影響較大［10－11］.

針對上述步長因子對AFS算法性能影響的問題，本文使用PSO 算法公式改進AFS算法，以減小步長因子對AFS 算法性能的影響.AFS 算法中魚的覓食、聚群和追尾行為的式（5）、（6）和（7）修改為如下新的公式：

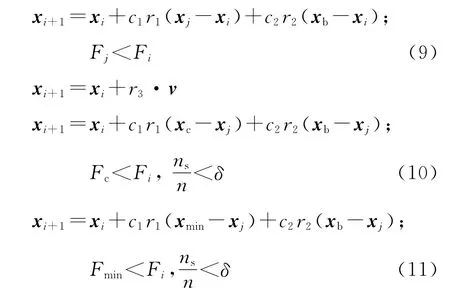
這樣AFS算法中的人工魚個體就可以像PSO算法中的粒子一樣，只依賴于視野因子而不依賴于步長因子進行游動行為的選擇，尋求最優解.

2.4 混沌機制

混沌（chaotic）是非線性系統中普遍存在的現象，具有確定性和遍歷性的特點.在群智能算法中，混沌機制的運用能夠提高種群的多樣性，進而避免算法出現過早收斂現象，增大搜索到全局最優的性能［7，12］.本文選取Logistic映射方法混沌初始化人工魚群位置，從而尋求SVR 參數全局最優組合.選取的混沌初始化映射方法公式為

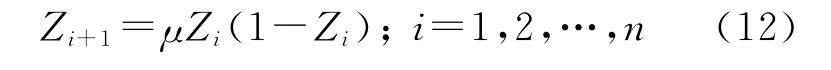
其中μ為控制參數，對系統狀態起關鍵作用.當μ＝4時，系統處于完全混沌狀態.

2.5 CPSOAFS－SVR模型

本文運用PSO 公式機制優化AFS的混合優化算法優化SVR，建立了混沌粒子群人工魚群混合優化SVR 的CPSOAFS－SVR 交通流量預測模型.模型具體流程如圖1所示.具體實現步驟如下：

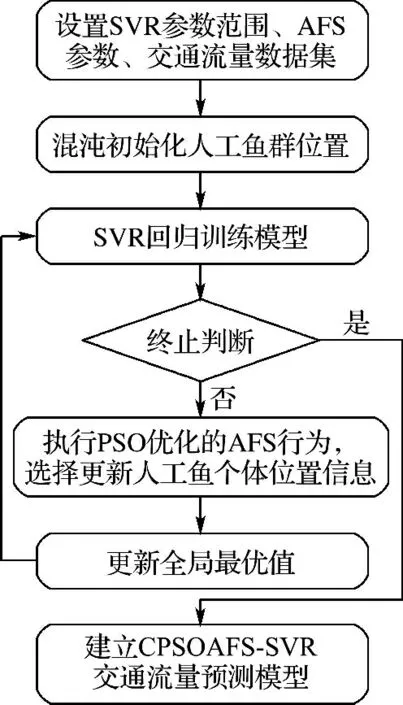
圖1 CPSOAFS－SVR 交通流量預測模型Fig.1 CPSOAFS－SVR traffic flow forecasting model

步驟1 數據集設置和參數初始化.將交通流量數據分為訓練集和測試集，進行數據預處理.設置SVR 的參數C、ε和σ的取值范圍以及PSO和AFS算法的初始參數.混沌初始化人工魚群位置.

步驟2 計算魚群的初始適應度.根據訓練集訓練SVR 模型，選出當前最優并記錄初始全局最優的人工魚的狀態，即參數組合（C，ε，σ）.

步驟3 人工魚行為選擇.每條人工魚分別執行混合魚群算法的覓食、聚群、追尾和隨機行為，更新人工魚個體的位置信息，保存全局最優值以及對應的SVR 參數組合.

步驟4 算法的終止判斷.判斷是否達到魚群的最大迭代次數，若不滿足則迭代次數加1，跳轉至步驟3繼續執行；若滿足則輸出魚群的最優適應度和最優值對應的SVR 參數組合，建立CPSOAFS－SVR交通流量預測模型，并用于測試集的回歸測試，檢驗測試性能.

3 仿真實驗及結果

本文分別采用混沌PSO 優化SVR（CPSOSVR）模型和混沌AFS 優化SVR（CAFS－SVR）模型作為參考模型，進行對比仿真實驗.

3.1 數據集準備

本文采用加利福尼亞高速公路性能評估系統（PeMS）采集的實際交通流量數據作為實驗數據來源，數據樣本時間間隔為5 min.實驗選取1d中的早6：00～10：00 的交通流量作為實驗數據集.實驗數據采用工作日情境下的5個站點數據，每個站點的訓練集有576個數據，預測第25d的48個數據.

實驗采用歷史時間序列的交通流量數據預測未來時刻的交通流量.設xi（t）為路段i上t時刻的交通流量，實驗采用前5個時間段的交通流量xi（t－5）、xi（t－4）、xi（t－3）、xi（t－2）和xi（t－1）作為輸入，xi（t）作為模型的預測輸出［3］.

3.2 評價指標和參數設置

為綜合比較各模型的仿真實驗結果和預測性能，實驗采用均方誤差ems、平均絕對百分誤差emap和均方根誤差erms共3個評價指標：

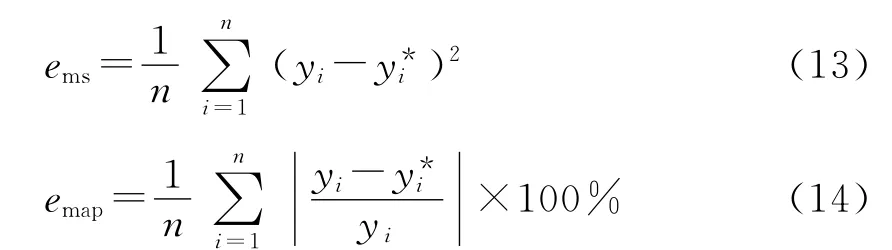
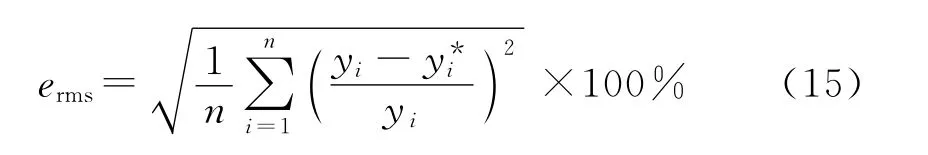
其中yi表示實際值，y＊i表示預測值，n為測試樣本個數.評價指標值越小，預測性能越好.

實驗的初始參數設置如表1所示.混合PSOAFS優化算法中參數與PSO 和AFS算法中的相同.

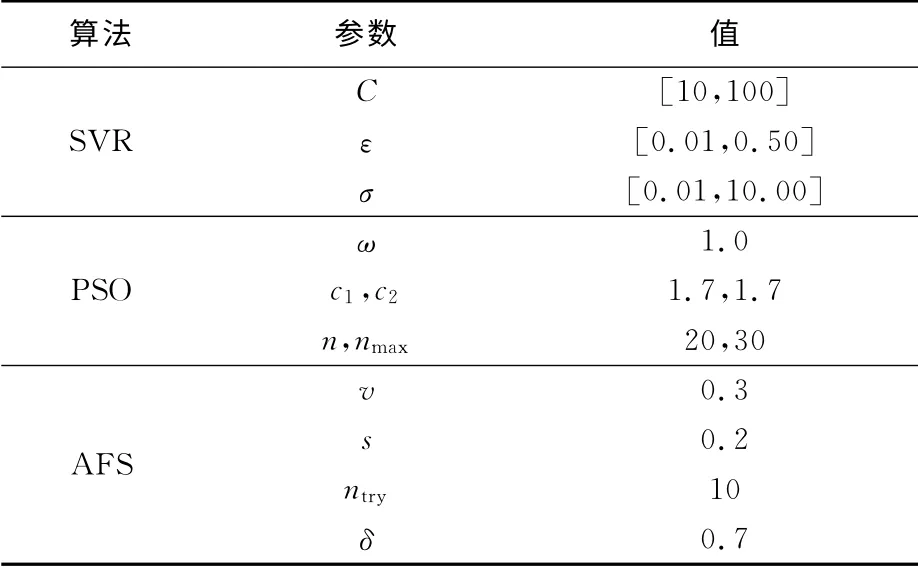
表1 初始參數設置Tab.1 Initial parameter settings

3.3 實驗結果和分析

本實驗 利 用libsvm－3.17 Matlab工具箱［13］實現了基于上述各算法優化支持向量回歸的交通流量預測模型.表2給出了站點1各個模型下選取的SVR 的參數C、ε和σ的最優組合.

表2 站點1各個模型的參數優化結果Tab.2 Parameter optimization results for each model on site 1

圖2顯示了站點1 的測試樣本在CPSOSVR、CAFS－SVR 和CPSOAFS－SVR模型下的預測值與實際值，表3給出了3個對比模型的評價結果.如圖2和表3所示，CPSO－SVR 和CAFS－SVR 模型預測結果相近，而本文提出的CPSOAFS－SVR 模 型 比CPSO－SVR 和CAFSSVR 模型的emap分別減小了8.9%和8.1%，提高了預測精度，證明了CPSOAFS－SVR 模型的準確性.

更一般的，分別對5個站點的數據集進行實驗，因為emap最能反映預測性能，所以表4給出了5個站點的emap.結果顯示，在不同站點的測試數據集情況下，CPSOAFS－SVR 模型都有最優的預測結果，其emap平均值為4.108%，比CPSO－SVR模型（emap平均值為4.312%）和CAFS－SVR 模型（emap平均值為4.274%）分別 減小了5.0%和4.0%，從而證明了CPSOAFS－SVR 模型的健壯性.

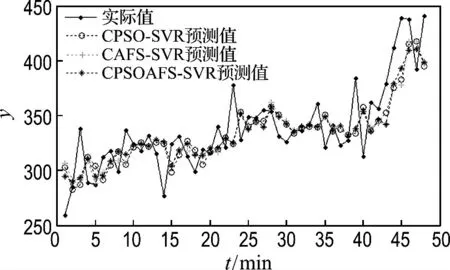
圖2 站點1各個模型的實際值與預測值Fig.2 Actual and predicted values for each model on site 1

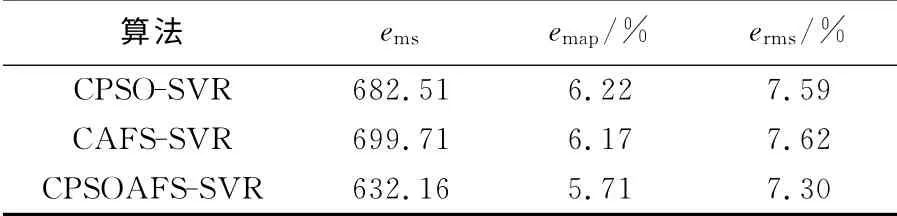
表3 站點1各個模型的評價結果Tab.3 Evaluation results for each model on site 1

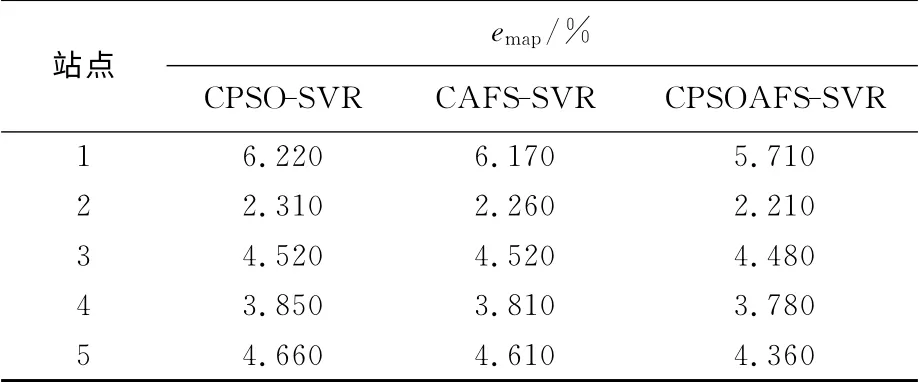
表4 5個站點的emap結果對比Tab.4 Comparison of 5sites′emapresults

4 結 語

準確的交通流量預測對交通控制系統是至關重要的，特別是在針對車流高峰期避免碰撞和提高交通效率方面.本文提出將基于混沌初始化機制的混合人工魚群算法優化SVR 的預測方法，應用到交通流量預測領域來研究模型的可行性.仿真結果表明，提出的CPSOAFS－SVR 交通流量預測模型比單一的PSO 和AFS 優化SVR 模型有更好的預測性能.模型良好的預測結果歸功于用PSO 算法減小了AFS 算法中步長因子的影響，從而選出更優的SVR 參數組合，并且混沌初始化機制的運用能夠更好地搜索解空間，取得最優預測值.未來將研究一些其他的混合群智能優化算法來更有效地解決交通流量預測問題.

［1］ Vlahogianni E I，Karlaftis M G，Golias J C.Shortterm traffic forecasting：Where we are and where we′re going［J］.Transportation Research Part C ：Emerging Technologies，2014，43：3－19.

［2］ 姚智勝，邵春福，高永亮.基于支持向量回歸機的交通狀態短時預測方法研究［J］.北京交通大學學報，2006，30（3）：19－22.YAO Zhi－sheng，SHAO Chun－fu，GAO Yongliang.Research on methods of short－term traffic forecasting based on support vector regression［J］.Journal of Beijing Jiaotong University，2006，30（3）：19－22.（in Chinese）

［3］ Castro－Neto M，Jeong Y S，Jeong M K，etal.Online－SVR for short－term traffic flow prediction under typical and atypical traffic conditions ［J］.Expert Systems with Applications，2009，36（3Part 2）：6164－6173.

［4］ Smith B L，Williams B M，Keith Oswald R.Comparison of parametric and nonparametric models for traffic flow forecasting ［J］.Transportation Research Part C：Emerging Technologies，2002，10（4）：303－321.

［5］ Vlahogianni E I，Karlaftis M G，Golias J C.Optimized and meta－optimized neural networks for short－term traffic flow prediction：A genetic approach［J］.Transportation Research Part C ：Emerging Technologies，2005，13（3）：211－234.

［6］ Hong W C，Dong Y，Zheng F，etal.Forecasting urban traffic flow by SVR with continuous ACO［J］.Applied Mathematical Modelling，2011，35（3）：1282－1291.

［7］ Hong W C.Traffic flow forecasting by seasonal SVR with chaotic simulated annealing algorithm［J］.Neurocomputing，2011，74（12－13）：2096－2107.

［8］ Fang N，Zhou J，Zhang R，etal.A hybrid of real coded genetic algorithm and artificial fish swarm algorithm for short－term optimal hydrothermal scheduling［J］.International Journal of Electrical Power and Energy Systems，2014，62：617－629.

［9］ 姚祥光，周永權，李詠梅.人工魚群與微粒群混合優化算法［J］.計算機應用研究，2010，27（6）：2084－2086，2102.YAO Xiang－guang，ZHOU Yong－quan，LI Yongmei.Hybrid algorithm with artificial fish swarm algorithm and PSO ［J］.Application Research of Computers，2010，27（6）：2084－2086，2102.（in Chinese）

［10］ 李曉磊.一種新型的智能優化方法——人工魚群算法［D］.杭州：浙江大學，2003.LI Xiao－lei.A new intelligent optimization method—artificial fish school algorithm ［D］.Hangzhou：Zhejiang University，2003.（in Chinese）

［11］ Tsai H C，Lin Y H.Modification of the fish swarm algorithm with particle swarm optimization formulation and communication behavior ［J］.Applied Soft Computing Journal，2011，11（8）：5367－5374.

［12］ LI Ming－wei，Hong Wei－chiang，KANG Hai－gui.Urban traffic flow forecasting using Gauss－SVR with cat mapping，cloud model and PSO hybrid algorithm［J］.Neurocomputing，2013，99：230－240.

［13］ Chang C C，Lin C J.LIBSVM：A library for support vector machines［J］.ACM Transactions on Intelligent Systems and Technology，2011，2（3）：27.