2缸發動機平衡機理研究及懸置系統優化設計

余良渭， 上官文斌， 唐穎， 李錦庭

(1. 華南理工大學機械與汽車工程學院， 廣東 廣州 510641； 2. 上汽通用五菱汽車股份有限公司， 廣西 柳州 545007)

?

·設計計算·

2缸發動機平衡機理研究及懸置系統優化設計

余良渭1， 上官文斌1， 唐穎2， 李錦庭2

(1. 華南理工大學機械與汽車工程學院， 廣東 廣州 510641； 2. 上汽通用五菱汽車股份有限公司， 廣西 柳州 545007)

以2缸發動機為研究對象，分析發動機曲柄活塞機構的運動規律，推導發動機在實際工作時產生的不平衡激勵力和力矩，研究2缸發動機的旋轉慣性力和往復慣性力的平衡方法，對一臺2缸發動機在不同平衡條件下產生的激勵進行數值模擬。在此基礎上，建立2缸發動機懸置系統優化模型，以懸置系統的固有頻率、能量解耦率和懸置動反力為優化目標，用序列二次規劃法進行多目標的優化，對一臺2缸柴油機進行了懸置系統優化設計。分析結果表明該優化方法可以有效減少發動機傳遞給車身的激勵。

2缸發動機； 平衡機理； 懸置系統； 多目標優化

目前轎車向著輕量化和燃油經濟化的方向發展，2缸發動機在轎車、微型車上的應用將越來越普及。但2缸發動機的平衡性較差，發動機本身的激振力較大，對整車的平順性不利。

要減小2缸發動機的激振力，需要減小發動機自身不平衡激勵。發動機的曲柄活塞機構工作時產生的旋轉慣性力可以通過在曲軸上相應位置加裝平衡重來平衡，而活塞運動的往復慣性力無法通過曲軸上的平衡重完全平衡，需要通過外加平衡軸來平衡[1]。 Karabulut[2]用一個3自由度的動態模型對一臺2缸四沖程發動機進行數值模擬，總結了曲軸上平衡質量的確定方法；Kim[3]提出平衡軸上平衡質量的大小、安裝位置的優化策略。另一方面，懸置系統的設計會很大程度地影響發動機傳遞給車身的振動大小。通過優化懸置的剛度、安裝位置和角度，可以使2缸機自身激勵傳遞給車身的力最小。上官文斌等從系統的固有頻率和能量解耦率出發，深入研究了動力總成懸置系統的設計及優化方法[4-7]。Akei等的研究表明，發動機懸置的剛度及安裝布置對懸置系統的整體減振性能有明顯影響[8]，而使用序列二次規劃法(SQP)進行懸置系統的優化設計可以有效減弱發動機經懸置傳遞給車身的力[9-10]。

本研究分析了2缸發動機缸體所受的不平衡激勵力(矩)，研究曲軸上加平衡重及平衡軸的平衡機理，分析2缸發動機懸置系統在不同平衡條件下產生的自身激勵；針對某2缸柴油機，以其懸置系統固有頻率、能量解耦率、懸置動反力為優化目標，以懸置的三向剛度和安裝位置為控制變量，建立2缸機懸置系統的多目標優化模型，得到懸置剛度及安裝位置的優化結果。

1 2缸發動機平衡性分析

每個缸內曲柄連桿機構的運動可以分為曲柄繞曲軸的旋轉運動和活塞、連桿沿氣缸內壁的往復運動。發動機缸體受到曲柄旋轉運動產生的旋轉慣性力、活塞組件往復運動產生的往復慣性力、缸內氣體燃燒的氣體力三者的共同作用。

單個曲柄連桿機構的旋轉慣性力Fr、往復慣性力Fj(見圖1)為

Fr=mrrω2,Fj=mjrω2(cosα+λcos2α)。

(1)

式中：ω為曲軸轉動的圓頻率；r為曲柄半徑;mr為每缸位于曲柄銷中心并繞曲軸軸線的旋轉運動質量；mj為每缸位于活塞銷中心沿氣缸中心線的往復運動質量；α為曲拐轉角；λ=r/l為連桿比，l為連桿大小頭的中心距。往復慣性力包括一階往復慣性力Fj1和二階往復慣性力Fj2兩部分：

Fj1=mjrω2cosα，Fj2=mjrω2λcos2α。

(2)

對于常見的2缸發動機，其曲柄分布見圖2，發動機坐標系的X軸沿曲軸中心線，指向發動機前端，Z軸平行于氣缸軸線，指向缸蓋，Y軸根據右手定則確定。

兩個缸的旋轉慣性力分別為Fr,1，Fr,2，大小相等，方向沿各自的曲柄，其合力Fr∑的大小為

Fr∑=|Fr，1+Fr，2│=2mrω2。

(3)

兩個缸的一階往復慣性力為Fj1，1，Fj1，2，二階往復慣性力為Fj2，1，Fj2，2，其大小分別為

Fj1，1=mjrω2cosα，Fj1，2=mjrω2cos(α-360°),

(4)

Fj2，1=mjrω2λcos2α，
Fj2，2=mjrω2λcos(2α-720°)。

(5)

兩個缸的一階往復慣性力合力Fj1∑、二階往復慣性力合力Fj2∑的大小為

Fj1∑=|Fj1，1+Fj1，2│=2mjrω2·cosα，

(6)

Fj2∑=|Fj2，1+Fj2，2│=2mjrω2λcos2α。

(7)

將合力Fr∑，Fj1∑，Fj2∑分別沿發動機坐標系各軸分解，則缸體在發動機坐標系下受到的作用力為

Fy=-Fr∑·sinα=-2mrrω2·sinα,

(8)

Fz=Fj1∑+Fj2∑+Fr∑cosα=2mjrω2·
cosα+2mjrω2λcos2α+2mrrω2·cosα。

(9)

以兩個缸的中心點為參考點，則兩個缸的旋轉慣性力、一階往復慣性力、二階往復慣性力產生的力矩矢量和為0。缸體在發動機坐標系下受到的作用力矩見圖3，其中Mx為發動機的輸出力矩。以兩個缸中心點為參考點時，My，Mz為0。

工程中發動機激勵一般以動力總成質心坐標系為參考，一般情況下2缸發動機的兩個缸的中心點與動力總成質心不重合，設2缸機的兩個缸中心點在整車坐標系下的坐標為 (XE,YE,ZE)，動力總成質心在整車坐標系下的坐標為(XCG,YCG,ZCG)，以動力總成質心為參考點，則2缸發動機缸體受到的不平衡力Fy,Fz產生的力矩為

My=Fz×(XCG-XE),

(10)

Mz=Fy×(XCG-XE),

(11)

Mx=-Fy×(ZCG-ZE)-Fz×(YCG-YE)。

(12)

2 2缸發動機的平衡方法

2缸發動機產生的旋轉慣性力Fr∑和一階往復慣性力Fj1∑數值上比較大，對發動機平衡性影響明顯，一般采用曲軸加平衡重和外加平衡軸的方式進行平衡。

2.1 曲軸平衡重平衡分析

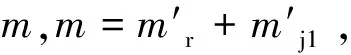
(13)

(14)

(15)

曲軸加平衡重后2缸發動機受到的不平衡力和力矩見表1。

表1 曲軸加平衡重后2缸機受到的不平衡力(矩)

2.2 一階平衡軸平衡分析

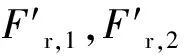
(16)

(17)

(18)

由于平衡軸與曲軸之間有偏心距離，平衡軸上平衡重產生的旋轉慣性力合力會產生繞X軸方向的附加力矩(見圖8)。

(19)

曲軸加平衡重且加一階平衡軸后2缸發動機受到的不平衡力見表2，受到的不平衡力矩見表3。

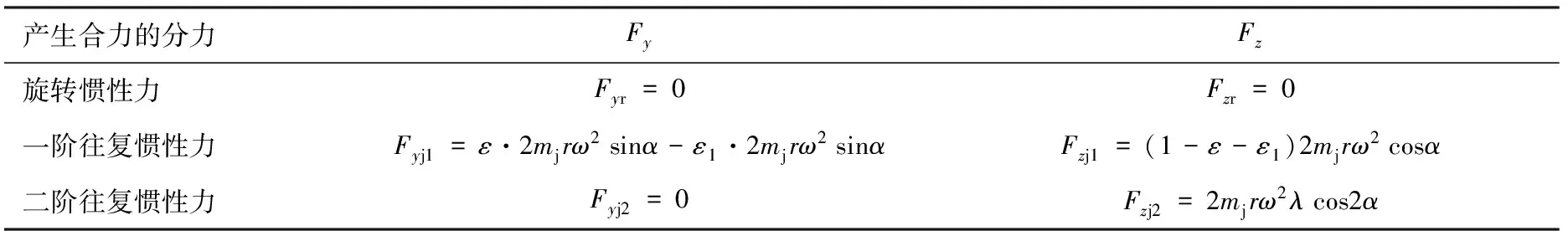
表2 曲軸加平衡重且加一階平衡軸后2缸機受到的不平衡力

表3 曲軸加平衡重且加一階平衡軸后2缸機受到的不平衡力矩

3 2缸發動機懸置系統優化設計

下面以一款2缸柴油機為例，分析該發動機在不同平衡條件下懸置系統的受力情況，使用序列二次規劃法進行懸置系統的多目標協同優化，并對比分析優化前后的懸置受力的情況。

3.1 2缸發動機懸置系統參數

圖9示出一發動機縱置的后驅轎車上的動力總成懸置系統。該動力總成使用三點懸置支撐，O—X0Y0Z0為整車坐標系，CG為動力總成質心，動力總成質心坐標系如圖中CG—XYA所示，OE—XEYEZE為以發動機兩個缸的中心點為原點建立的發動機坐標系。

該2缸發動機的質量及慣性參數見表4，發動機曲柄連桿機構參數見表5，各懸置在局部坐標系下的初始靜剛度及懸置在汽車坐標系中的安裝位置見表6，實測該2缸發動機的缸壓曲線見圖10。

表4 動力總成的質量及慣性參數

表5 曲柄連桿機構參數

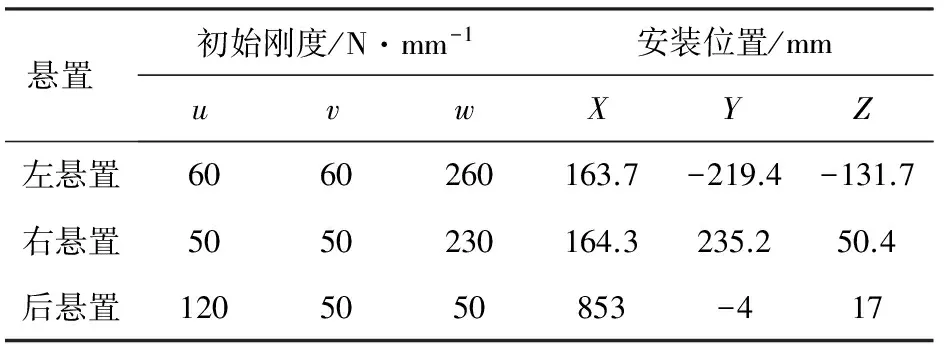
表6 懸置的初始剛度及在汽車坐標系中的安裝位置

該2缸機動力總成的質心在整車坐標系下的坐標為(208，-13，7)，發動機采用三點懸置支撐的形式，兩個前懸置V型布置，主要起支撐和防扭作用，后懸置輔助支撐。該懸置系統在動力總成重力作用下的靜態位移見表7。一般動力總成懸置系統要求預載位移小于5mm，從表7可以看出，該懸置系統滿足靜態平衡要求。

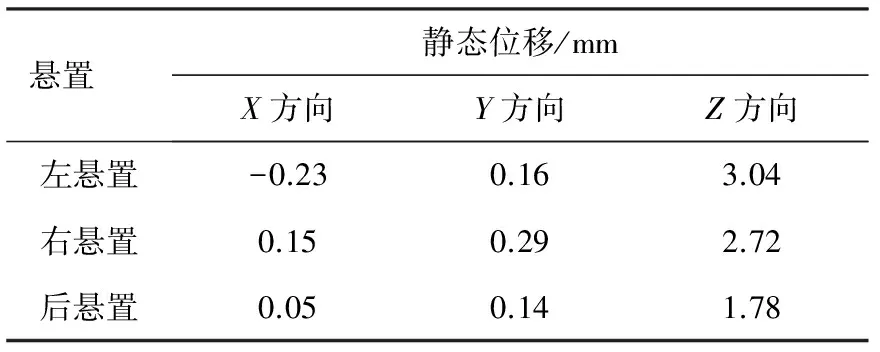
表7 懸置靜態預載位移

3.2 不同平衡條件下的發動機激勵分析

在不采取任何平衡措施的情況下，發動機的曲柄活塞機構的旋轉慣性力、一階往復慣性力、二階往復慣性力都處于不平衡的情況，此時2缸發動機由于曲柄連桿機構運動的慣性力產生Fy,Fz兩個方向的不平衡力激勵(見圖11)，同時還有Mx,My,Mz3個方向的不平衡力矩激勵(見圖12)。

曲軸上加平衡重可以實現100%平衡旋轉慣性力和按一定比例平衡一階往復慣性力。用于平衡一階往復慣性力的平衡重會產生水平方向的附加力，故一般用曲軸加平衡重的方式平衡50%的一階往復慣性力。這種平衡情況下發動機整體結構簡單，產生的不平衡激勵見圖13和圖14。

在加裝平衡軸的情況下，2缸發動機的不平衡力激勵Fz(見圖15)只剩下二階往復慣性力，且二階往復慣性力較小。此時發動機產生的不平衡力矩激勵見圖16。

3.3 懸置系統優化設計

在設計發動機懸置系統時，一般將動力總成簡化為空間中的六自由度剛體模型，主要考慮其六階固有頻率和六個自由度的解耦率。懸置固有頻率和解耦率計算方法詳見文獻[11]，考慮固有頻率和解耦率的優化目標函數形式見文獻[7]。對于2缸發動機，在不同平衡條件下自身激勵不同，從而懸置受力也不同。本研究在設計2缸發動機的懸置系統時，同時考慮固有頻率、能量解構率及懸置動反力3個方面的要求，建立目標函數的表達式為

式中：ω1，ω2，ω3分別為總的固有頻率權系數、總的解耦率權系數和總的動反力權系數;αi為第i個自由度固有頻率的權系數，βi為第i個自由度的解耦率的權系數，γi為第i個懸置的動反力的權系數。

Si為各階固有頻率與目標頻率的差值，具體定義式如下：

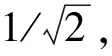
理想情況下懸置系統各自由度的解耦率最大為100%，由于布局的限制，實際中難以達到100%，一般設定解耦率下限值decli為75%，從而定義各自由度的解耦率在優化目標函數中的表達式Ti為

本研究取2缸機在完全平衡狀態(旋轉慣性力,一階、二階往復慣性力完全平衡)下懸置的動反力作為“動反力目標值”，試圖通過對懸置的優化，使得2缸機在不平衡或者部分平衡狀態下，懸置點的動反力等于或者小于發動機完全平衡時懸置點的動反力。

懸置系統的固有特性取決于懸置的剛度、安裝位置和角度等。本算例中的2缸柴油機的懸置安裝角度已經固定，故取3個懸置的三向剛度和安裝位置為優化變量，設為

{X}={ku1，kv1，kw1，x1，y1，z1，…
kui，kvi，kwi，xi，yi，zi，…}。

式中：kui，kvi，kwi為第i個懸置的三向靜剛度值；xi，yi，zi為第i個懸置的安裝位置。

考慮懸置的可制造性，懸置的靜剛度有上下限的約束，不同方向之間的剛度值有一定的比例關系約束。2缸機的懸置剛度比例約束見表8。懸置安裝位置限制為初始位置坐標±5mm的范圍。

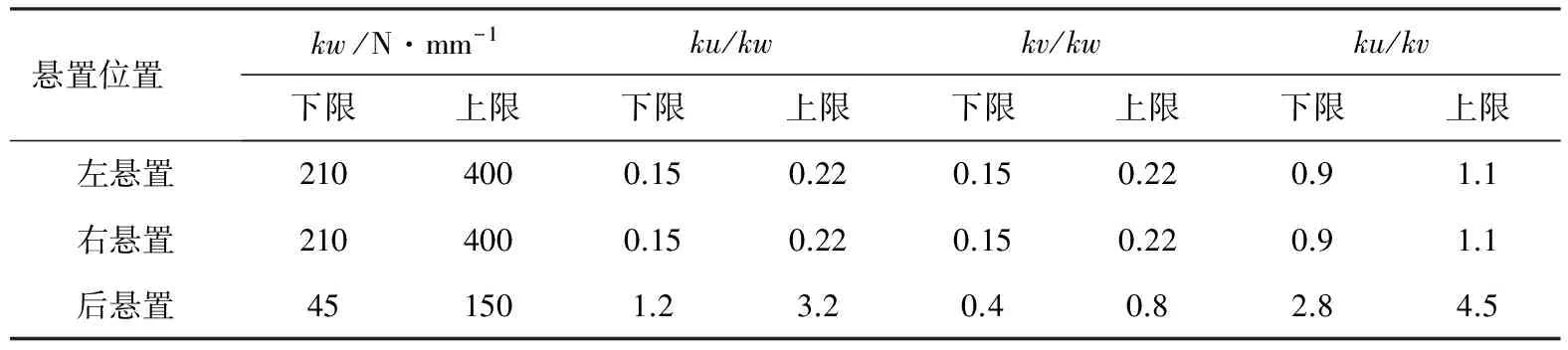
表8 懸置的剛度比例約束

本研究使用序列二次規劃法(SQP)，將此問題轉化為簡單的二次規劃問題進行迭代求解。優化后的懸置剛度和安裝位置信息見表9。

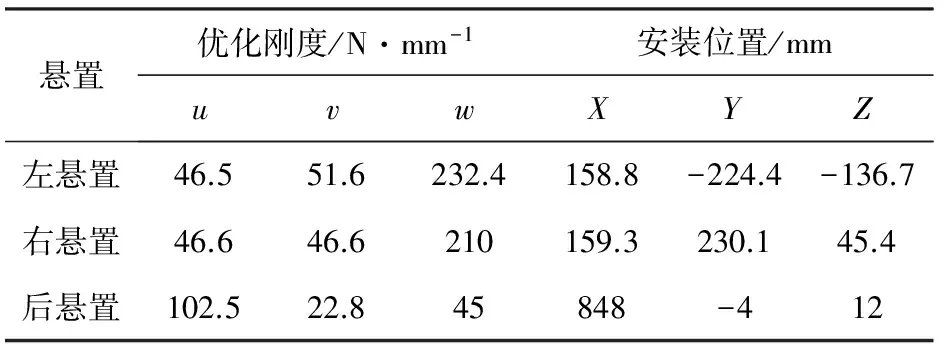
表9 優化后懸置的剛度及安裝位置

本研究中的2缸發動機實際采用了曲軸加平衡重且外加一階平衡軸的方式進行平衡，在此基礎上進行了懸置系統的優化設計，優化后的懸置動力情況見圖17和圖18。

在不采取任何平衡措施的情況下，2缸發動機會產生較大的不平衡激勵，導致3個懸置的受力都較大。在曲軸上加平衡重，平衡了100%的旋轉慣性力和50%的一階往復慣性力，懸置的受力情況明顯變好。在此基礎上外加一根平衡軸，用于平衡50%的一階往復慣性力，懸置受力情況進一步改善。在發動機的機械結構確定之后，發動機自身的不平衡激勵已經無法改變，此時從懸置系統的角度出發，對懸置的剛度和安裝位置進行優化，可以在不需改變發動機機械結構的情況下減少發動機傳遞給車身的不平衡激勵。從圖17和圖18可以看出，懸置剛度和安裝位置的優化對懸置在低轉速下的受力情況有較為明顯的改善。

4 結論

a) 在曲軸上加平衡重可以平衡曲柄活塞機構的旋轉慣性力和部分一階往復慣性力；在發動機上加平衡軸可以平衡部分一階往復慣性力，平衡軸與曲軸上的平衡重配合使用，產生的附加力互相抵消，可實現完全平衡一階往復運動慣性力；

b) 通過合理地布置懸置安裝位置，調整懸置三向剛度，可以在不改變發動機機械結構的情況下，進一步優化懸置在發動機不平衡激勵下的受力情況，減少發動機傳遞給車身的振動。

[1]SuhKH,LeeYK,YoonHS.Astudyonthebalancingofthethree-cylinderenginewithbalanceshaft[C].SAEPaper2000-01-0601.

[2]KarabulutH.Dynamicmodelofatwo-cylinderfour-strokeinternalcombustionengineandvibrationtreatment[J].InternationalJournalofEngineResearch,2012,13(6):616-627.

[3]KimC,KangYJ,LeeB,etal.Determinationofoptimalpositionforbothsupportbearingandunbalancemassofbalanceshaft[J].MechanismandMachineTheory,2012,50:150-158.

[4]ShangguanWen-Bin.Enginemountsandpowertrainmountingsystems:areview[J].InternationalJournalofVehicleDesign,2009,49(4):237-258.

[5] 上官文斌,黃天平,徐馳,等.汽車動力總成懸置系統振動控制設計計算方法研究[J].振動工程學報,2008,20(6):577-583.

[6]ShangguanWB,ZhaoY.Dynamicanalysisanddesigncalculationmethodsforpowertrainmountingsystems[J].InternationalJournalofAutomotiveTechnology,2007,(6):731-744.

[7] 陳大明.動力總成懸置系統剛體模態優化設計及位移計算方法[D].廣州：華南理工大學, 2012.

[8]AkeiM,KouzatoK，UyamaT.StudyofEngineMountLayoutforIndustrialDiesel[C].SAEPaper2012-32-0108.

[9]TaoJS.DesignOptimizationofMarineEngine-mountsystem[J].JournalofSoundandVibration,2000,235 (3):477-494.

[10]AmbardekarMN,LogeshkumarN,GangurdePR,etal.VibrationIsolationofaPick-upVehiclewitha2-CylinderDieselEngine[C].SAEPaper2007-26-035.

[11] 徐石安.汽車發動機彈性支承隔振的解耦方法[J].汽車工程,1995,17(4):198-204.

[編輯: 李建新]

Balance Mechanism and Optimization of Mounting System of 2-Cylinder Engine

YU Liangwei1, SHANGGUAN Wenbin1, TANG Ying2, LI Jinting2

(1. School of Mechanical and Vehicle Engineering, South China University of Technology, Guangzhou 510641， China；2. SAIC-GM-Wuling Automobile Co., Ltd., Liuzhou 545007， China)

Taking a 2-cylinder engine as an object, the motion law of piston-crank mechanism was analyzed and the unbalanced forces and moments under actual operating condition were deduced. Then the balance method of rotating and reciprocating inertia forces for the 2-cylinder engine was researched and the impacts under different balance conditions were simulated. Moreover, the optimized model of mounting system for the 2-cyliner engine was built and the optimization of natural frequency, energy decoupling rate and mount dynamic reaction force were carried out with the sequence quadratic programming (SQP) method. The optimization of mounting system for the 2-cylinder engine shows that the method can reduce the engine excitation transferred to vehicle body effectively.

2-cylinder engine; balance mechanism; mounting system; multi-objective optimization

2015-03-17;

2015-05-25

余良渭(1991—)，男，碩士，研究方向為汽車系統動力學；349733684@qq.com。

10.3969/j.issn.1001-2222.2015.06.001

TK421.5

B

1001-2222(2015)06-0001-07