[0,1]-拓撲空間中T*分離性的非標準分析方法研究

馬春暉, 史艷維, 翟美娟

(1.西安建筑科技大學 理學院, 西安 710055; 2.西安培華學院 基礎部, 西安 710125)

?

[0,1]-拓撲空間中T*分離性的非標準分析方法研究

馬春暉1*, 史艷維2, 翟美娟1

(1.西安建筑科技大學 理學院, 西安 710055; 2.西安培華學院 基礎部, 西安 710125)

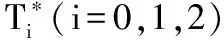
非標準擴大模型; 準分離; 模糊集的鄰域; 模糊集的單子

1 預備知識

在一般拓撲學[1]中,許多深刻的結果都是要求拓撲空間具有某種分離性,對于[0,1]-拓撲空間而言,情形也是一樣,因此對[0,1]-拓撲空間中的分離性進行深入研究是非常有必要的.自1968年,C. L. Chang[2]以L. A. Zadeh[3]的模糊集理論為骨架創立[0,1]-拓撲學以來,模糊分離性就成為了[0,1]-拓撲學的研究熱點之一.1975年和1977年,B. Hutton先后提出了模糊正則性[4]和模糊完全正則性[5]的概念,這些分離性及其特征刻畫與一般拓撲學中一種傳統的方法是平行的.1980年蒲保明和劉應明[6]在研究模糊點的鄰近結構時,基于模糊點的重域,首次提出了準T0,T0,T1和T2分離性的概念,并對這些分離性進行了系統地討論.之后,王國俊在文獻[7-8]中利用模糊點的遠域重建了T分離性.在一般拓撲學中,分離性有多重不同的等價形式,但在[0,1]-拓撲學中以這些熟知的分離性為藍本來建立的模糊分離性卻不等價,于是從不同角度來推廣一般拓撲學中的同一分離性可以得到不同的模糊分離性.在文獻[7-8]中,王國俊在T分離性的基礎上,建立了一套系統的T*分離性,這種分離性有別于T分離性,也是一種“好的推廣”(good extension).

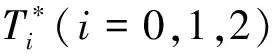
為行文方便,先來回顧一些非標準分析和[0,1]-拓撲學中的基本概念,詳細內容可以參見文獻[8-11].

如果S≠?滿足以下條件:(1) 對于任意的x∈S,x≠?;(2) 對于任意的x∈S,y?x(?y∈S),則稱S是個體集.對于個體集S,歸納定義:

V0(S)=S;Vn+1(S)=Vn(S)∪2Vn(S),

n=0,1,2,…,

定義1設個體集S是無限集,如果映射*:V(S)→V(*S)滿足以下條件:

(1)*?=?;

(2) 對于任意的s∈S,*s=s;

(3) 轉換原理成立,即|=α當且僅當*|=*α,其中,α是LV(S)中的有界量詞語句,*α是將α中的常量c替換為*c得到的LV(*S)中的有界量詞語句;

(4) 共點原理成立,即對于任意的V(S)中的共點關系r,存在y∈V(*S),使得〈*x,y〉∈*r(?x∈dom(r)),

則稱V(*S)是個體集S的非標準擴大模型.

本文總假設X是無限集,[0,1]是單位閉區間,X∪[0,1]?S,且V(*S)是S的非標準擴大模型.

關于模糊點的單子有如下性質,詳細的證明可以參見文獻[12].

2 主要結果

定義4設(X,δ)是[0,1]-拓撲空間,對于任意X上的模糊點xλ,yμ,當xλ與yμ準分離時:

定理1設(X,δ)是[0,1]-拓撲空間:

證明僅證(3),結論(1)和(2)類似可證.

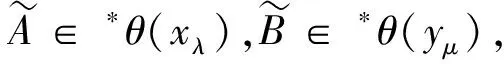
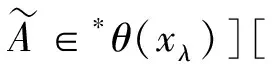
由轉換原理可得,如下有界量詞語句在V(S)中成立,

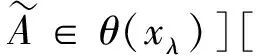
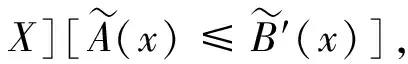
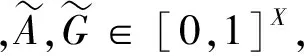
可見,模糊集的單子是模糊點的單子的推廣,關于模糊集的單子,也有類似于引理1的結論:

證明考慮如下V(S)中的二元關系

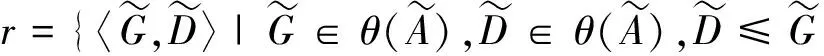
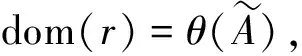
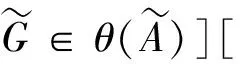
由轉換原理可得如下V(*S)中的有界量詞語句成立,

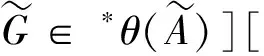
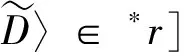
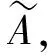
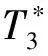
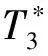
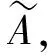
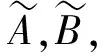
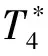
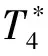
[1]KelleyJL.GeneralTopology[M].NewYork:VanNostrand, 1955.

[2]ChangCL.Fuzzytopologicalspaces[J].JMAA, 1968, 24:182-190.

[3]ZadehLA.Fuzzysets[J].InformationControl, 1965, 8: 338-353.

[4]HuttonB.Normalityinfuzzytopologicalspaces[J].JMAA, 1975, 50:74-79.

[5]HuttonB.Uniformitiesonfuzzytopologicalspaces[J].IBID, 1977, 58:559-571.

[6]PuBaoming,LiuYingming.FuzzytopologyI,NeighborhoodstructureofafuzzypointandMoore-SmithConvergence[J].JMAA, 1980, 76: 571-599.

[7] 王國俊. 拓撲分子格的分離公理[J]. 數學研究與評論, 1983, 3(2): 9-16.

[8] 王國俊.L-Fuzzy拓撲空間論[M]. 西安: 陜西師范大學出版社, 1988.

[9]RobinsonA.NonstandardAnalysis[M].Amsterdam:North-Holland, 1963.

[10]DavisM.AppliedNonstandardAnalysis[M].NewYork:Wiley, 1977.

[11]CutlandNJ.Nonstandardmeasuretheoryanditsapplications[J].BullLondonMathSoc, 1983,15: 529-589.

[12] 馬春暉, 陳東立, 史艷維. [0,1]-拓撲空間中的單子及其逼近原理[J]. 純粹數學與應用數學, 2007, 23(1): 108-111.

A study inT*separations by nonstandard analysis methods in [0,1]-topological spaces

MA Chunhui1, SHI Yanwei2, ZHAI Meijuan1

(1.School of Science, Xi'an University of Architecture and Technology, Xi’an 710055;2.Department of Basic Courses, Xi'an Peihua University, Xi'an 710125)

nonstandard enlarged model; pre-separated; neighborhood of fuzzy set; monad of fuzzy set

2014-10-08.

陜西省自然科學基金項目(2007A12); 陜西省教育廳專項科研基金項目(2013JK0574); 西安建筑科技大學人才科技基金項目(RC1239).

1000-1190(2015)02-0167-04

O141.41

A

*E-mail: ma-chunhui@163.com.