一個能量輸運穩態模型弱解的存在性

董建偉, 周永衛

(鄭州航空工業管理學院 數理系, 鄭州 450015)

?

一個能量輸運穩態模型弱解的存在性

董建偉*, 周永衛

(鄭州航空工業管理學院 數理系, 鄭州 450015)

考慮一個簡化的半導體能量輸運穩態模型.在Dirichlet-Neumann混合邊界條件下,利用截斷方法和Leray-Schauder不動點定理得到了其模型弱解的存在性.研究結果表明,即使熱導率與電子溫度有關,如果歐姆聯結部分的電子密度是正的,則半導體器件內部的電子密度也是正的.

能量輸運模型; 穩態解; 存在性

1 主要結果

漂移-擴散模型、能量輸運模型和流體動力學模型是描述亞微半導體器件中載流子運動規律的三大類宏觀模型. 它們通過宏觀量例如載流子密度、電流密度、載流子溫度和電位勢來描述半導體器件的宏觀性質. 由于漂移-擴散模型未考慮熱電子效應,在半導體器件的模擬中會給出不準確的結果,而完整的流體動力學模型形式過于復雜,不便于進行數值模擬,于是許多數學家和物理學家開始轉向研究能量輸運模型. 最近,Jungel等人考慮了一個簡化的能量輸運模型[1]:

nt-div((nθ)+nV)=0,

(1)

(2)

-λ2ΔV=n-C(x),x∈Ω,t>0,

(3)

其中,電子密度n、電子溫度θ和電位勢V為未知函數;μ(n,θ),θL(x)分別表示熱導率與晶格溫度;C(x)稱為摻雜函數,用來描述摻雜物質正離子的密度結構;τ,λ>0分別表示能量弛豫時間和標度的德拜長度;Ω?Rd(d=1,2,3)為半導體器件所占據的有界區域.模型(1)～(3)可以從流體動力學方程組中出,詳情見文獻[1].

文獻[1]在Dirichlet-Neumann混合邊界條件下得到了模型(1)～(3)弱解的整體存在性,但由于技巧原因,他們所取的熱導率μ(n,θ)僅僅依賴于電子密度n,這并不十分符合物理實際. 在半導體器件模型中,熱導率不僅與電子密度有關,往往也與電子溫度有關,例如文獻[2-3]中都取熱導率μ(n,θ)=nθ.

本文將在μ(n,θ)=nθ的情形下研究模型(1)～(3)的穩態方程組:

-div(θn)=div(n(θ+V)),

(4)

(5)

-λ2ΔV=n-C(x),x∈Ω.

(6)

假設區域Ω的邊界?Ω∈C0,1,?Ω=ΓD∪ΓN,ΓD∩ΓN=?,ΓN是閉集,ΓD的d-1維Lebesgue測度是正的,即measd-1ΓD>0.ΓD表示半導體器件的歐姆聯結部分,ΓN表示絕緣邊界部分. 于是,提出如下邊界條件:

n=nD,θ=θD,V=VD,x∈ΓD,

(7)

n·ν=θ·ν=V·ν=0,x∈ΓN,

(8)

其中,ν表示?Ω上的單位外法向量.

主要結果敘述如下:

注1Jungel等人還提出了一個帶量子項的簡化能量輸運模型,關于這方面的研究結果可以參考文獻[4-6].

2 結果的證明

由于(4)、(5)兩個方程都是退化的,所以考慮如下截斷問題:

-div(θm,Mn)=div(nk,K(θ+V)),

(9)

(10)

-λ2ΔV=nK-C(x),x∈Ω,

(11)

其中,

nK=max{0,min{K,n}},

nk,K=max{k,min{K,n}},

θm,M=max{m,min{M,θ}},

k,K,m,M的定義見定理1.

定理1的證明需要如下引理1:

引理1設定理1中的條件成立,且(n,θ,V)∈(H1(Ω))3是問題(9)～(11),(7),(8)的解,則

‖θ‖H1(Ω)≤C1,‖V‖H1(Ω)≤C2,‖n‖H1(Ω)≤C3,

且00僅可以與nD,θD,VD,θL(x),C(x)及Ω,d有關.

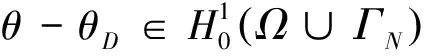
其中,|Ω|表示Ω的Lebesgue測度,所以存在常數C1>0,使‖θ‖H1(Ω)≤C1.

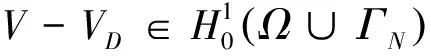
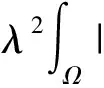
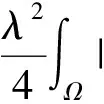
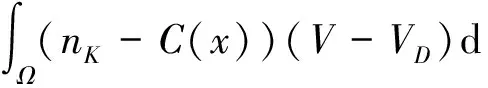
(12)

由帶ε的Young不等式和Poincare不等式知

(13)

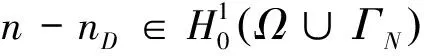
所以再由‖θ‖H1(Ω)≤C1及‖V‖H1(Ω)≤C2知,存在常數C3>0,使‖n‖H1(Ω)≤C3.

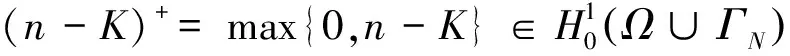
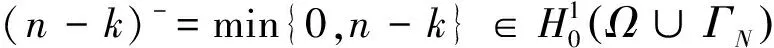
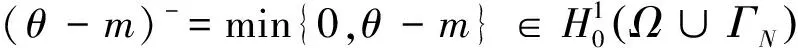
的唯一解,并設θ∈H1(Ω)是問題

的唯一解,其中,σ∈[0,1]. 則不動點算子

V0=VD,x∈ΓD,V0·ν=0,x∈ΓN,

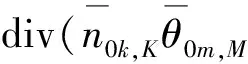
θ0=σ0θD,x∈ΓD,θ0·ν=0,x∈ΓN,

-div(θ0m,M(θ0+V0)),x∈Ω,

n0=σ0nD,x∈ΓD,n0·ν=0,x∈ΓN

的解,所以T連續.從而由Leray-Schauder不動點定理知,問題(9)～(11),(7),(8)存在解(n,θ,V)∈(H1(Ω))3.又因為k≤n≤K,m≤θ≤M,所以nk,K=n,nK=n,θm,M=θ,從而問題(9)～(11),(7),(8)的解也是問題(4)～(8)的解. 證畢.

[1]JungelA,PinnauR,RohrigE.Existenceanalysisforasimplifiedenergy-transportmodelforsemiconductors[J].MathematicalMethodsintheAppliedSciences, 2013, 36(13): 1701-1702.

[2]GardnerC.Thequantumhydrodynamicmodelforsemiconductordevices[J].SIAMJournalonAppliedMathematics, 1994, 54: 409-427.

[3]JungelA,MatthesD,MiliusicJP.Derivationofnewquantumhydrodynamicequationsusingentropyminimization[J].SIAMJournalonAppliedMathematics, 2006, 67: 46-68.

[4]JungelA,MiliusicJP.Asimplifiedquantumenergy-transportmodelforsemiconductors[J].NonlinearAnalysis:RealWorldApplications, 2011, 12: 1033-1046.

[5]ChenLi,ChenXiuqing,JungelA.Semiclassicallimitinasimplifiedquantumenergy-transportmodelforsemiconductors[J].KineticandRelatedModels, 2011, 4: 1049-1062.

[6]DongJianwei,ZhangYoulin,ChengShaohua.Existenceofclassicalsolutionstoastationarysimplifiedquantumenergy-transportmodelin1-dimensionalspace[J].ChineseAnnalsofMathematics,SeriesB, 2013, 34(5): 691-696.

Existence of weak solutions to a stationary energy-transport model

DONG Jianwei, ZHOU Yongwei

(Department of Mathematics and Physics, Zhengzhou Institute of Aeronautical Industry Management, Zhengzhou 450015)

A simplified stationary energy-transport model for semiconductors is considered. Under the mixed Dirichlet-Neumann boundary conditions, the existence of weak solutions to the model is obtained by using the truncation method and the Leray-Schauder fixed-point theorem. It is shown that, although the thermal conductivity depends on the electron density, the electron density stays positive in the semiconductor device if it is positive on the parts of Ohmic contacts.

energy-transport model; stationary solution; existence

2014-09-19.

河南省科技廳基礎與前沿技術研究計劃項目 (132300410373);河南省教育廳科學技術研究重點項目(12A110024);鄭州航空工業管理學院青年科研基金項目(2013111001).

1000-1190(2015)02-0179-03

O175.2

A

*E-mail: dongjianweiccm@163.com.