聯合格構式構架多向風荷載作用下力學性能分析

程 達

(安徽省電力設計院，安徽 合肥 230601)

大跨度聯合格構式構架在國內電力行業相關的工業建筑結構的應用中并不常見。考慮其設計、施工等各方面因素的在國內的局限性，少有應用。

1 本構關系

通過文獻[1—8]資料整理及相關工程總結，在統一強度理論基礎上，提出了結構鋼彈塑性本構模型，此模型不僅適用于拉壓強度相同的鋼材，而且適用于拉壓強度不同的結構鋼。

1.1 鋼材應力應變理論分析

聯合式格構式構架的主要材料為角鋼，為了建立合理的三維空間有限元模型，需要定義鋼材合理的本構關系。鋼材的應力應變經歷彈性階段，彈塑性階段，塑性階段，應變強化階段，見圖1。

比例極限σp：直線段的最大應力值。其實嚴格來說，比σp略高處還有彈性極限，但兩者極其接近所以將σp看成是彈性極限。

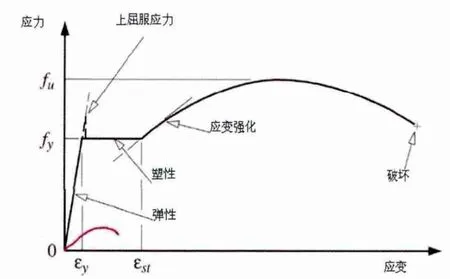
圖1 應力應變模型

屈服應力fy：應變ε在σp之后漸漸加大，應力應變成曲線關系一直到屈服點，這是彈塑性階段，此后應力保持不變而應變持續發展，形成水平線段即屈服平臺，這是塑性流動階段。應力超過σp之后任一點的變形都包括彈性變形和塑性變形兩部分，其中塑性變形在卸載后不再恢復，也成為參與變形或永久變形。

1.2 本構模型選取

根據鋼材應力應變理論，鋼材應力在達到屈服應力fy之前，鋼材接近理想彈性體，fy之后塑性應變范圍很大而應力保持不變，所以接近理想塑性體。文獻[9]對塑性設計的規定就是以鋼材是理想彈塑性體的假設為依據，忽略了應變硬化的有利作用。

鋼材有屈服平臺并且屈服平臺末端的應變比較大，這就有足夠的塑性變形來保證截面上的應力最終都達到fy，因此一般的強度計算中不考慮應力集中和殘余應力。在拉桿中截面的應力按均勻分布計算即以此為基礎。從而確立本文格構式構架的鋼材可以定義為理想彈塑性模型進行空間有限元模擬計算分析。

2 聯合格構式構架模型定義

2.1 荷載定義

通過文獻[9，10]采用50年一遇基本風壓，將平交及45°風向作用于模型主體結構上，分別對兩個平交方向和45°作用方向的作用結果進行比較分析，并根據設計以及實際工程應用的需要，按照構架所受的恒荷載、活荷載(導線拉力、導線覆冰荷載等)、地震反應譜建立不同荷載工況。

2.2 風荷載體型系數μs

本文重點研究了聯合格構式構架模型在不同方向風荷載作用下對的力學性能，故不同風向下風荷載體型系數μs是風荷載計算的重要影響系數，文獻[11，12]均給出了不同的風荷載體型系數μs計算方法。

針對本文研究的電力工程中的聯合格構式構架模型，根據文獻[12]中給出的90°風向和對角風向下體型系數的計算方法，通過定義系數：

通過計算不同格構式梁柱的Φ，從而得出聯合格構式構架不同桿件的風荷載體形系數μs，并代入文獻[12]中風荷載標準值計算公式：

式中：z為高度處的風振系數；βz為風壓高度變化系數；μz為基本風壓值；w0通過文獻[11，12]均可查出。

如前所述，通過文獻[12]給出的風荷載體形系數μy的計算方法，可以得出本文研究的聯合格構式構架模型在兩個平交方向和45°作用方向所需要的可靠的多向風荷載輸入數據。

2.3 結構體系布置

構架在各個方向均受不同的導線拉力作用，在滿足工藝條件下，選擇合理的格構柱和橫梁的角鋼規格，圖2、圖3給出了聯合格構式構架的單根格構柱局部透視圖，構架平面圖，三維透視圖。

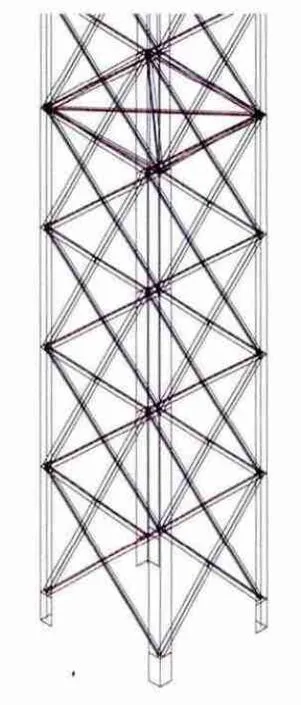
圖2 單根格構柱局部透視圖

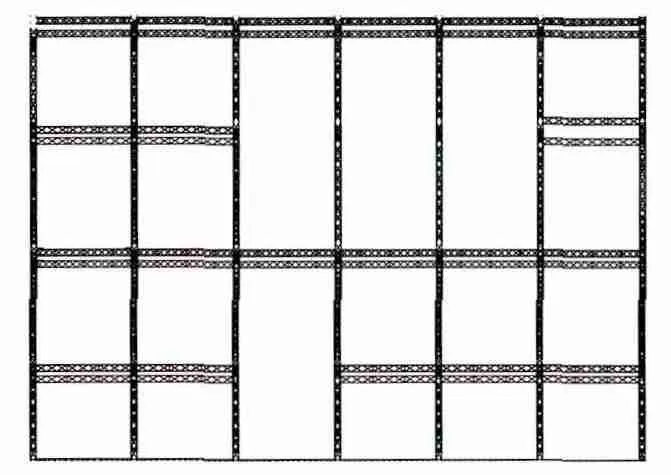
圖3 聯合格構構架平面布置圖

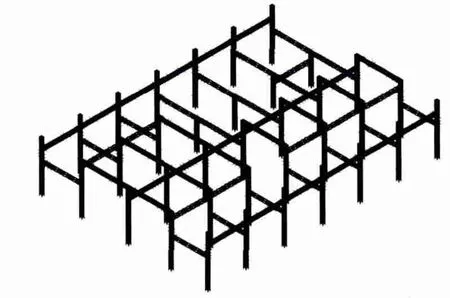
圖4 聯合格構式構架三維透視圖

3 計算結果分析

針對計算結果，挑選聯合格構式構架中邊跨、中跨10個典型受力構件及節點，在相同的恒荷載及活荷載條件下，分別比較在正交風向1(0°風向)，正交風向2(90°風向)，斜交風向3(45°風向)三種不同風荷載工況作用下，各柱腳節點及構架主材的應變性能，找出可用于該結構基礎設計的控制應力以及驗算結構主材是否滿足不同風向作用。

3.1 柱腳反力曲線

邊跨及中跨柱腳節點拉力、壓力分布見圖5—圖8。

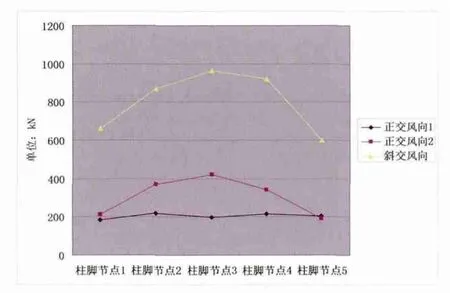
圖5 邊跨柱腳節點拉力分布曲線

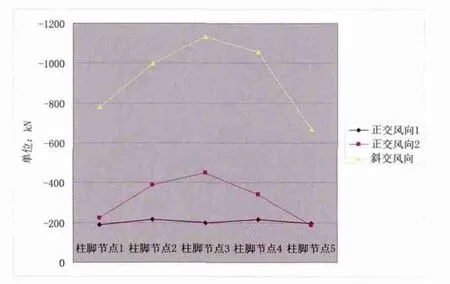
圖6 邊跨柱腳節點壓力分布曲線

通過圖5、圖6，可知邊跨五個柱腳節點反力(拉、壓力)由外而內呈現拋物線型分布，邊跨中部節點拉壓反力最大；三種不同工況作用下，45°風作用下的柱腳反力最大，該工況為設計需考慮的控制工況。

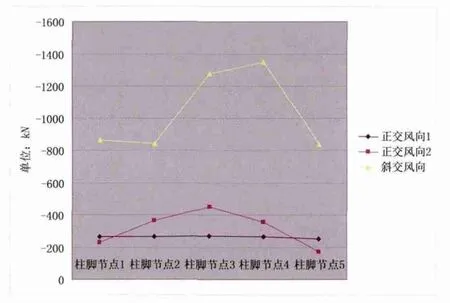
圖8 中跨柱腳節點壓力分布曲線

通過圖7、圖8，可知中跨中部柱腳節點或靠近中部拉壓反力最大；三種不同工況作用下，45°風作用下的柱腳反力最大，該工況為設計需考慮的控制工況。由于中跨橫梁及導線布置，使得中跨柱腳反力最大值并未出現在中間格構柱柱腳節點。

3.2 格構構件應變云圖

圖9 正交風向1應變云圖

格構構件應用云圖見圖9—圖11。

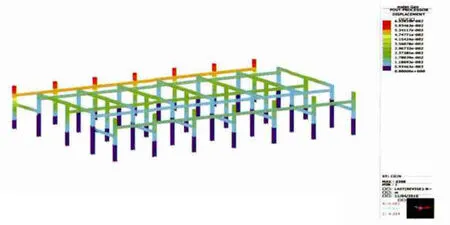
圖10 正交風向2應變云圖

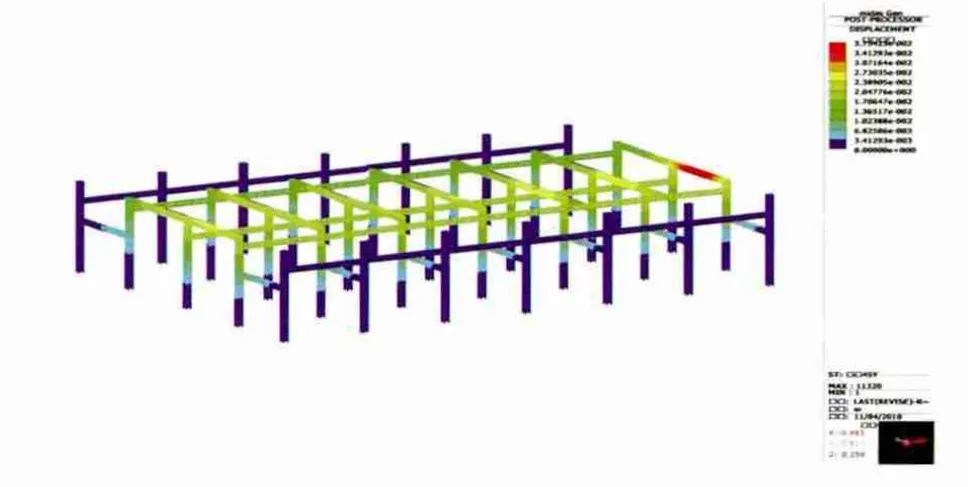
通過圖9—圖11應變云圖，不難發現，在正交風向作用下，結構主材的應變最大，即正交風向作用下的應力可以作為驗算構架主材是否滿足工程需要的依據；同時，也應考慮斜交風向作用下局部節點及角鋼的驗算。

4 結語

通過計算結構比較分析，發現本文提及的聯合格構式構架，在實際工程中用于基礎計算的主導風向應為45°斜交風向：

(1)通過格構柱柱腳反力曲線，發現風向在45°工況下，柱腳拉壓力最大；

(2)通過聯合格構構件應變云圖，可知風向在0°，90°工況下，聯合構架式構架構件的應變最大。

(3)用于結構設計的聯合格構式構架基礎設計的控制應力工況是45°風荷載作用，用于格構構架主材設計的控制應力工況是04°，90°作用。

本文分析比較了三個主導風向作用下的聯合格構式構架的柱腳節點反力和應變，三維空間有限元模型有效的模擬了實際工程中的構架，比較得出可用于計算及設計的控制工況反力和應變，彌補了電力工業領域中聯合格構式構架在多風向作用下計算分析的欠缺，可以應用推廣到類似的工程應用中。

[1]錢令希，等．中國大百科全書：力學篇[M]．北京：中國大百科全書出版社，1985．

[2]俞茂宏，何麗南，宋凌宇．雙剪應力強度理論及其推廣[J]．中國科學(A)，1985．12(85)．

[3]YuMao－hong．Twinshearstressyieldcriterion[J]．lnt．J．ofMechanicalScience，1985，25(1)．

[4]俞茂宏．雙剪理論及其應用[M]．北京：科學技術出版社，1998．

[5]趙均海，等．用同一強度理論和同一滑移線場理論求解某些塑性平面應變問題[J]．機械工程學報，1999．35(6)．

[6]蔣有諒．非線性有限元法[M]．北京：北京工業學院出版社，1988．

[7]張汝清，詹先義．非線性有限元分析[M]．重慶：重慶大學出版社，1990．

[8]FukumotoY, KusamaH.Localinstabilitytestsofpaltee lementsundercyclicuniaxialloading[J].J.of Struct．Engng，ASCE，1985，111(5)．

[9]GB50017－2003，鋼結構設計規范[S]．

[10]GB50135－2006，高聳結構設計規范[S]．

[11]GB5009－2012，建筑結構荷載規范[S]．

[12]DL/T5457－2012，變電站建筑結構設計技術規程[S]．