平原地區常年與五年一遇最高內澇水位的確定

潘曉春，王曉惠

(江蘇省電力設計院，江蘇 南京 211102)

1 概述

根據現行架空輸電線路勘測設計規程，對于平原地區或內澇地區塔位，常要求提供常年最高內澇水位或5年一遇最高內澇水位，以用于輸電線路基礎防澇設計。然而，規程卻未明確給出常年最高內澇水位的概念或定義，又因在條文里這兩個水位常以“或”相連同時出現，易給人以等同視之的理解。那么，應如何認識常年最高內澇水位？其重現期幾何？與5年一遇最高內澇水位是否相當呢？

平原地區水位觀測站一般設置于圩外干河上，而圩內地區往往缺乏實測內澇水位系列資料。只有在遭遇較為稀遇(如重現期30年及以上)的暴雨洪澇而大面積破圩時，洪澇水合二為一，圩區內外水位趨于一致。對于稀遇程度不高的洪澇，由于圩堤的阻隔，圩外河流水位與圩內地面內澇積水水位可能存在一定的差異，因此難以取外河水位站資料直接采用頻率分析的方法，來分析確定沿線塔位5年一遇及常年最高內澇水位。本文基于暴雨產流原理，來簡略推求平原地區5年一遇及常年最高內澇水位，并結合對蘇北平原地區典型的農田、魚塘等平斷面的現場查勘，對推算成果進行合理性檢查。

2 常年最高內澇水位的重現期

2.1 概念描述

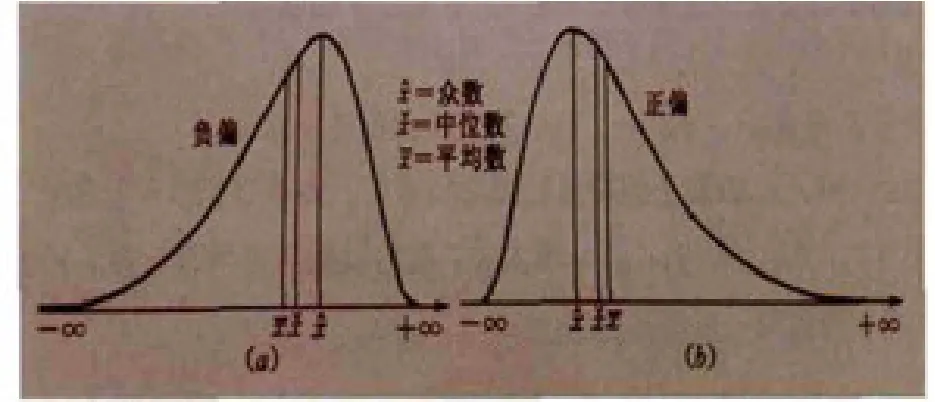
圖1 平均數、中位數和眾數在概率密度曲線上的相對位置(a)負偏；(b)正偏

與洪水位一樣，可以把內澇水位視作隨機變量來研究。對于隨機變量通常有相對于某個中心位置的集中或離散的描述。因此，需要用一些隨機變量的數字特征來表征這些中心位置。平均數、中位數和眾數即屬于此類最基本的數字特征。

平均數是以觀測值頻率為權的加權平均值，亦稱數學期望；中位數系把密度函數曲線下的面積劃分為各等于0.5的兩個部分時所對應的觀測值；眾數是表示密度函數的高峰所對應的觀測值。

對于連續型概率分布，若密度函數曲線是單峰且對稱時，則平均數、中位數和眾數三者合而為一；而若分布曲線不對稱，但偏值不大時，則三者的關系見圖1。河流歷年枯水流量及枯水位、海域歷年低潮位可能屬于負偏，其余包括洪澇水位在內的水文氣象隨機變量大多呈現為正偏。

從基本概念來看，平均數、中位數以及眾數均屬于表征概率密度分布的中心位置，因而均可用于描述常年最高內澇水位。

2.2 重現期分析

若分別以歷年最高內澇水位的平均數、中位數以及眾數來表征常年最高內澇水位，則對應的出現頻率或重現期分別是多少呢？

顯然，中位數對應的頻率為50%，相應重現期為2年，這與隨機變量服從何種分布無關，但中位數的具體可能略有差異。平均數、眾數的重現期與隨機變量的概率分布函數有關，下文假設歷年最高內澇水位分別服從Pearson—Ⅲ型分布和極值Ⅰ型分布，來推算評價平均數、眾數的重現期。

2.2.1 Pearson—Ⅲ型分布

Pearson—Ⅲ型分布的概率密度函數和分布函數分別為

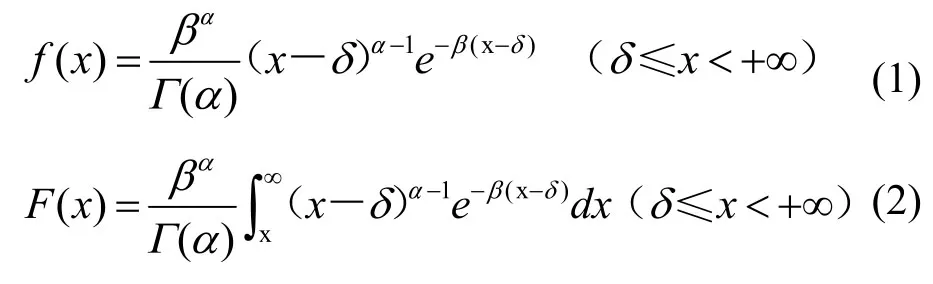
式中：Γ(α)為α的伽瑪函數；α、β、δ為分別為形狀、尺度和位置參數。α、β均大于零。

由矩和參數的關系推證，Pearson—Ⅲ型分布的三個參數與三個統計參數均值x－、離差系數Cv以及偏態系數Cs具有如下關系：

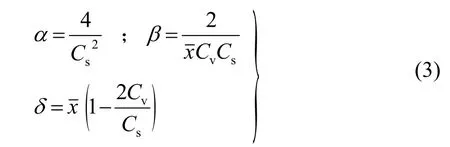
直接由分布函數計算設計值非常麻煩，實際工作中通過引進標準化變量——離均系數ΦCS,P，利用變換后式(4)計算設計值。

由式(4)可知，當ΦCS,P=0時，xP=。

對于平原地區年洪澇水位而言，其偏態系數Cs一般介于0.4～1.4之間。據此查Pearson—Ⅲ型分布ΦCS,P表可知，當P=40%～50%時，ΦCS,P=0。亦即若以Pearson—Ⅲ型分布來描述平原最高內澇水位，則平原最高內澇水位平均數的重現期2.5年～2年。

對式(1)求導

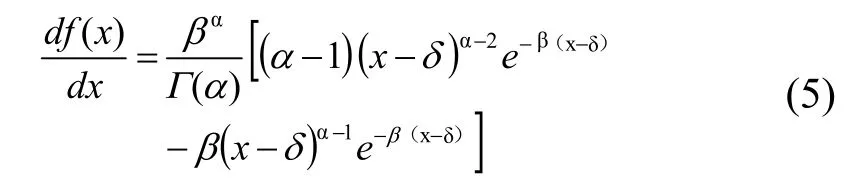
對于連續性概率分布，眾數x^就是使得密度函數f(x)取最大值時所對應的x值，亦即滿足令式(5)等于零，同時考慮到式(3)，得眾數x^與統計參數的關系式為

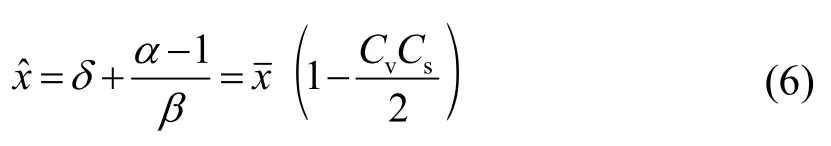
據此查 Pearson—Ⅲ型分布 ΦCs，P表，當Cs=0.4～1.4，滿足式(7)的P=50%～70%，亦即若以Pearson—Ⅲ型分布來描述平原最高內澇水位，則其眾數的重現期2年～1.4年。

2.2.2 極值Ⅰ型分布

極值Ⅰ型分布亦稱耿貝爾(Gu mbel)分布，其密度函數和分布函數分別為：

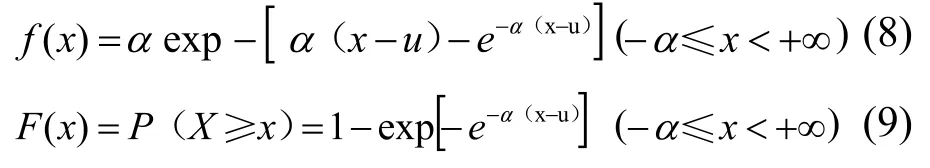
式中：μ為分布的位置參數；α為分布的尺度參數。

本分布偏態系數Cs為恒等于1.1395471...的常數。同樣可以采用標準化變量，按照式(4)計算設計值。離均系數ΦP按下式計算：

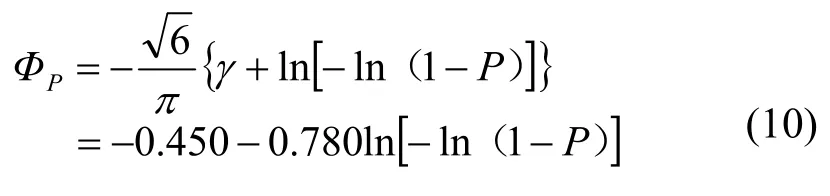
式中：γ為歐拉常數，γ=0.57721566。

當 ΦP=0 時，則 xP=，P=1-exp[-e—γ]=0.4296，這說明平均數固定在42.96%的超過概率處。因而，若以極值Ⅰ型分布來描述平原最高內澇水位，則其平均數的頻率約43%，相應重現期約2.3年。

對式(8)求導并令其等于零，同時考慮分布參數與一階原點矩的關系，可解出

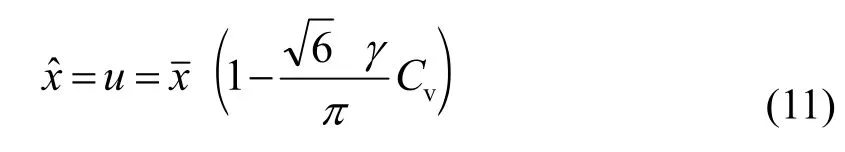
式(11)表明極值Ⅰ型分布的位置參數即為眾數，對應的超過概率為P=1－e—1=0.6321。因而，若以極值Ⅰ型分布來描述平原最高內澇水位，則其眾數的頻率約63%，相應重現期約1.6年。

[例]今有A、B、C三座水位站，假定洪澇水位服從Pearson—Ⅲ型和極值Ⅰ型分布，則分別應用前文相關公式計算均值、眾數、中位數及其相應重現期，成果見表1、表2。

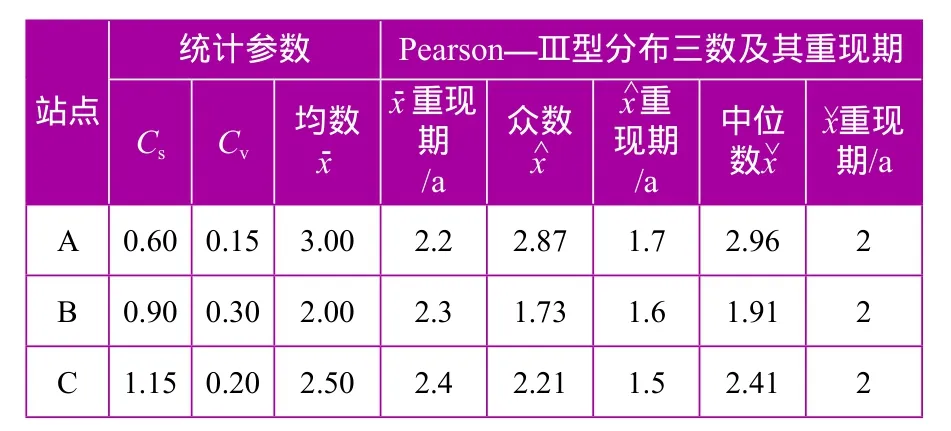
表1 A、B、C三站最高內澇水位Pearson—Ⅲ型分布三數及其重現期

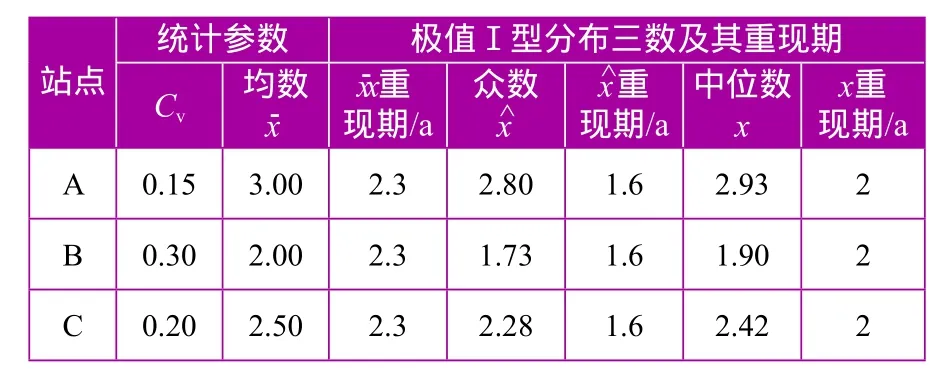
表2 A、B、C三站最高內澇水位極值Ⅰ型分布三數及其重現期

2.2.3 匯總分析

綜合上文成果，平原最高內澇水位的中位數、平均數、眾數相應頻率及重現期見表3。

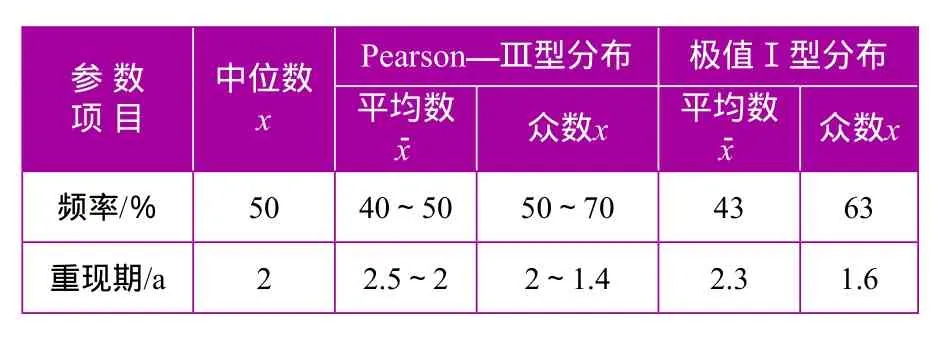
表3 平原最高內澇水位的中位數、平均數、眾數相應頻率及重現期

由表3可見，對于極值Ⅰ型分布，三數的頻率(重現期)均是定值；而對于Pearson—Ⅲ型分布，除中位數外，平均數、眾數的頻率(重現期)均為與偏態系數有關的區間值。

安全起見和便于操作，筆者建議取平均數，即“歷年平均最高內澇水位”或“頻率為40%(2.5年一遇)最高內澇水位”來定義“常年最高內澇水位”，或在規程條文里以詞義更明確的前者直接代之。

3 由設計暴雨推求常年和5年一遇最高內澇水位

幾項假定：(1)雨澇同頻；(2)因稀遇程度不高，不考慮澇水外排；(3)汛期土壤濕潤滿蓄，不考慮下滲損失；(4)平原圩區，圩堤防洪能力一般20年～30年一遇，可抵御外河洪水，只考慮本地降雨致澇。

基于上述假定，則推求常年(2.5年一遇)最高內澇水位和5年一遇最高內澇水位即可簡化為簡單的線性疊加問題，采用下式計算：

式中：ZP為頻率為P的最高內澇水位，對常年和5年一遇最高內澇水位P分別取40%和20% ；為塔位所在田間的平均地面高程；α為田間降雨蓄水率；D—為汛期暴雨前田間平均積水深；HP為頻率為P的設計暴雨量。

式(12)中的參數，根據現場情況按如下方法考察、計算確定(以蘇北中部平原圩區為例)：

(1)田間降雨蓄水率α反映的是平原地區容蓄降雨的比率，小于1。蘇北中部平原區取0.90；(2)應基于汛期的田間狀態(旱地、水田等)，合理確定暴雨前田間平均水深D—的取值。對于蘇北平原地區，旱地一般取0～0.10 m，水稻田一般取0.10 m～0.20 m；(3)對于平原地區，HP按最大三日暴雨量計算取值，而不是小流域雨洪計算采用的最大24h暴雨量，且不作點面折減。

根據《江蘇省暴雨參數圖集》，查得蘇北中部平原區最大三日暴雨量統計參數，并由此計算最大三日設計暴雨量，見表4。

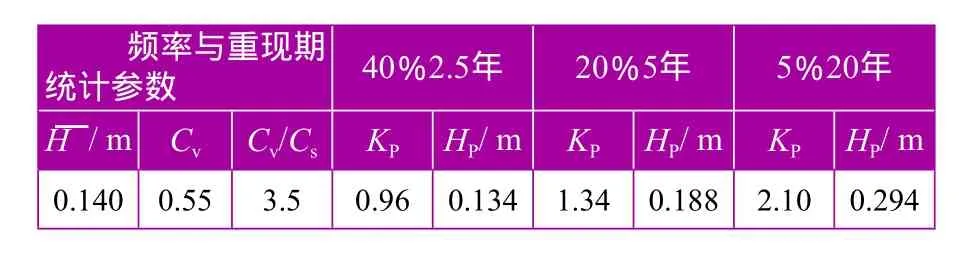
表4 蘇北中部平原區最大三日暴雨量統計參數及設計暴雨量

將各項參數及表4成果，代入式(12)算得蘇北中部平原地區汛期旱地與水稻田的常年最高內澇水位和5年一遇最高內澇水位計算公式，見式(13)、式(14)。

4 常年和5年一遇最高內澇水位的現場查勘

蘇北平原地區圩堤防洪能力一般達20年～30年一遇的標準，典型水田平面示意見圖2。

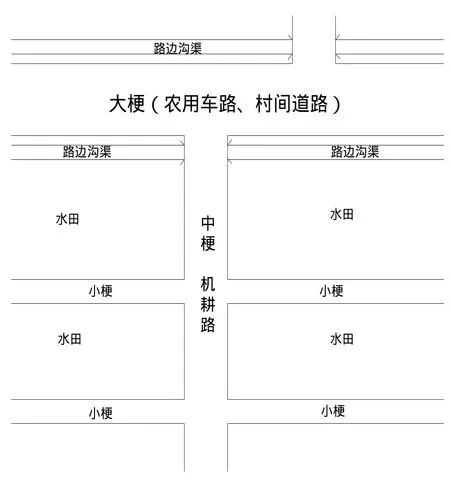
圖2 蘇北平原地區典型水田平面示意圖

一般而言，田間小梗、中梗、大梗頂面高程逐級抬高。根據現場多處實測，中梗一般寬約2.0 m～2.5 m，作為機耕路一般要保證“常年”機耕通行，其頂面大多高于兩側田間地面0.20 m～0.40 m，可以確定常年最高內澇水位的參考；而作為農用車道或村間道路的大梗，一般寬約3.5 m～4.5 m，其頂面大多高于兩側田間地面0.30 m～0.50 m，可以視作5年一遇最高內澇水位的參考。

當然，在野外勘測過程中，并不能總是遇見如此典型的水田結構分布，應注意觀察地形地貌并基于當地雨澇特性，合理確定常年最高內澇水位和5年一遇最高內澇水位。

例如，蘇北中部地區分布有眾多的人工魚塘和蟹塘，這些水塘大多在原有田面的基礎上直接推梗圈圍而成，其四周塘埂一般高于外周田面甚多。汛期正處魚蟹養殖季節，塘內會保持足夠的水深及水量。若遇集中暴雨，池塘水位上升，若高于塘埂頂部則漫溢外周農田。因此，若塔基立于塘中，其常年最高內澇水位及5年一遇最高內澇水位則可參照塘埂頂部高程確定。

5 結語

(1)對于可視作隨機變量的內澇水位，可用平均數、中位數以及眾數來描述常年最高內澇水位。假定平原區最高內澇水位服從極值Ⅰ型分布，平均數、中位數以及眾數的重現期均為定值，分別為2.3年、2年以及1.6年；而對于Pearson—Ⅲ型分布，平均數、中位數以及眾數的重現期分別為2.5年～2年、2年以及2年～1.4年。

(2)最高內澇水位的分析確定具有很強的經驗性，現場查勘時應留意周邊地形地貌、道路田埂與田面的相對高差，調查汛期而非踏勘期的田間狀態及相應持水水深，并基于當地設計暴雨推算設計最高內澇水位，進而合理取值。

(3)應注意把握內澇水位勘測及分析計算成果的合理性。一般來說，同一地點常年最高內澇水位、5年一遇最高內澇水位以及歷史最高內澇水位逐級升高。

(4)安全起見和便于操作，筆者建議取“歷年平均最高內澇水位”或“頻率為40%(2.5年一遇)最高內澇水位”來定義“常年最高內澇水位”，或在規程條文里以詞義更明確的前者直接代之。

(5)建議適當提高輸電線路基礎防澇設計標準，據表4等數據測算，若由5年一遇提高至20年一遇，蘇北平原地區最高內澇水位約増加0.10 m，基面有限抬高，鐵塔呼高相應降低，不一定增加造價，卻可顯著提高基礎抵御淹澇的能力。

(6)值得注意的是，位于河流、湖泊、水庫及行滯蓄洪區的水中塔基，應滿足行蓄洪要求及自身防洪安全，根據防洪評價或規程防洪要求，按照某一稀遇頻率的洪水位進行設計。此類水體中的塔位設計洪水位的分析確定方法不在本文討論范圍之列。對于圩堤防洪能力低于5年一遇或不設防的內澇區，應考慮外洪侵襲影響塔位，本文方法不適用于此類情形的設計最高內澇水位的分析確定。

[1]GB 50545－2010，110kV～750 kV架空輸電線路設計規范[S]．

[2]DL/T5076－2008，220 kV及以下架空送電線路勘測技術規程[S]．

[3]GB 50548－2010，330 kV～750 kV架空輸電線路勘測規范[S]．

[4]GB 50741－2012，1000 kV架空輸電線路勘測規范[S]．

[5]孫濟良，等．水文氣象統計通用模型[M]．北京：中國水利水電出版社，2001．

[6]叢樹錚．水科學技術中的概率統計方法[M]．北京：科學出版社，2010．