方變圓的體積計算

陳棽棽，韋迎旭

(河南省電力勘測設計院，河南 鄭州 450007)

1 概述

目前由于工程優化及降低造價的要求，在火力發電廠煤倉間內煤斗儲煤量滿足鍋爐最大連續蒸發量工況耗煤小時數符合相關規程的前提下，力爭降低煤倉間輸煤皮帶層的標高以及提高煤斗的充滿系數，這樣煤斗的形狀除了傳統的平壁型(圖1)、圓錐型(圖2)、雙曲線漸縮型(圖3)等以外，還出現了如方變圓(也稱方圓節)型和褲衩腿型等異形煤斗；為了方便、準確地計算這些異形煤斗的幾何容積(體積)，有必要明確其理論計算公式。

圖1 平壁型

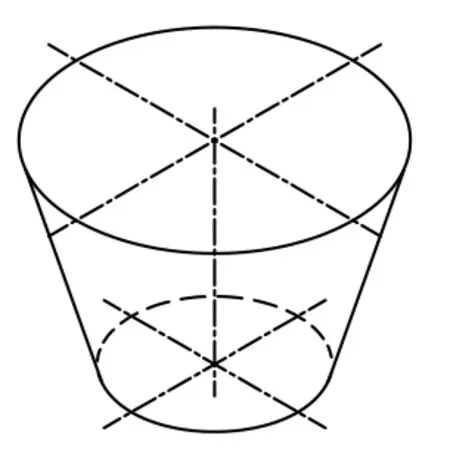
圖2 圓錐型

圖3 雙曲線漸縮型

而方變圓形狀幾何體的體積在大多數書籍和資料中未列出過其通用的計算公式，本文試圖采用數學積分的方法進行推導，從而得出其通用公式。

另外，關于方變圓形狀幾何體的表面積計算，也是我們所關心的內容。但由于這牽涉到更加復雜的推導和計算，甚至不能用解析式表達出來(涉及橢圓積分)，需要通過計算機數值算法才能得出，筆者將在另文中加以討論，本文中不再贅述。

2 方變圓幾何體的主要尺寸特征值

典型的方變圓幾何體見圖4。

其矩形端所在的平面與圓形端所在的平面是平行的。

將矩形端的兩邊長分別用a和b表示，圓形端的半徑用R表示，方形端平面與圓形端平面間的距離用h表示。矩形中心與圓形圓心在水平方向上的偏差，即偏心距分別用c和d表示。

圖4 方變圓幾何體的主要尺寸特征值

3 積分求解方變圓的體積公式推導

首先建立一個三維直角坐標系，為了計算方便，將原點定于圓形端的圓心上，見圖5。

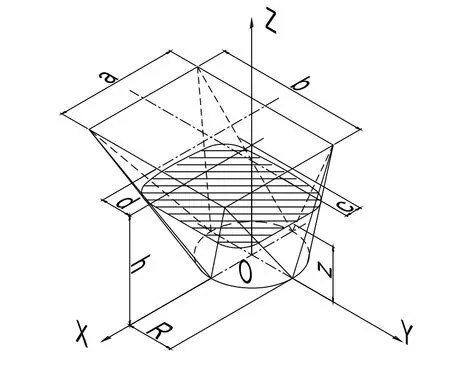
圖5 三維直角坐標系中的方變圓

設想在Z坐標方向的一定高度z上平行于方變圓上下兩端平面截取一個截面s，可以推導出s的形狀見圖6。

圖6 截面s的形狀

截面s的截面積S的計算公式見式(1)：

則方變圓的體積V的計算公式為：

式(2)即為方變圓幾何體體積的通用理論計算公式，從式中可以看出其體積僅與矩形端和圓形端的幾何尺寸以及兩端間的距離(即h，也可稱為高)有關，而與兩端中心的偏心距無關。

4 運用拆解變形方法驗證體積公式

祖暅是我國南北朝時期著名數學家祖沖之之子，也是一名杰出的數學家，提出了著名的“祖暅原理”。

祖暅原理，又名等冪等積定理，原文為“冪勢既同，則積不容異。”，內容是：夾在兩個平行平面間的兩個幾何體，被平行于這兩個平行平面的任何平面所截，如果截得兩個截面的面積總是相等，那么這兩個幾何體的體積相等。

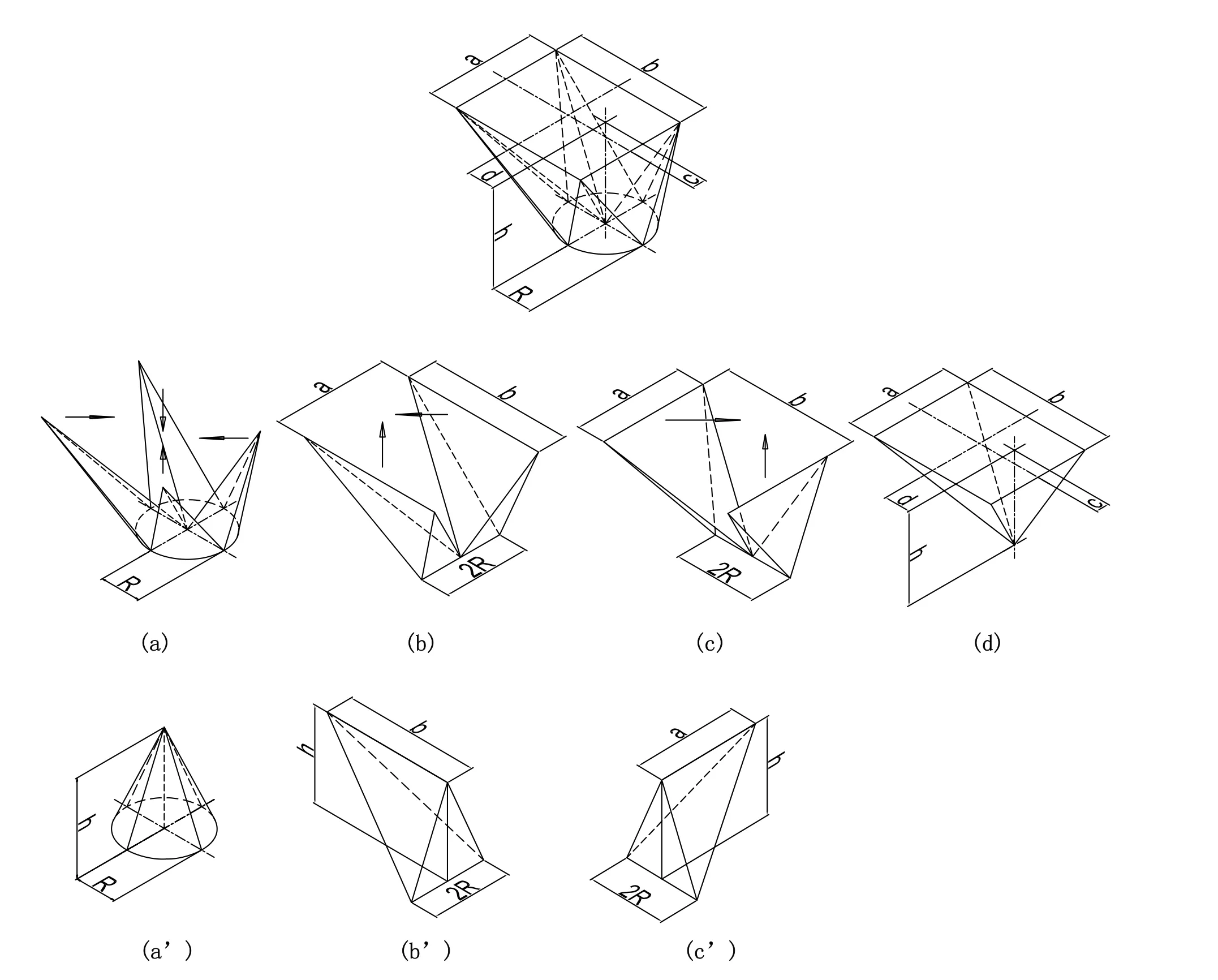
圖7 方變圓拆解變形示意圖

從祖暅原理的表述中可以看出，其本質也是與數學積分相同的；這就為我們采用拆解變形的方法來驗證方變圓體積的計算公式提供了依據。

從圖7中可以看出原先的方變圓可拆解為四個部分：(a)、(b)、(c)、(d)，而將其中的(a)、(b)、(c)繼續等體積分別變形為(a’)、(b’)、(c’)，則(a’)可形成一個正圓錐，(b’)和(c’)均形成一個三棱錐，而(d)是一個四棱錐。

可以簡單地看出，(a’)的體積為πR2h/3，(b’)的體積為bRh/3，(c’)的體積為aRh/3，而(d)的體積為abh/3；而原先的方變圓體積是(a’)、(b’)、(c’)和(d)四部分的總和，這樣就與式(2)的結果是完全一致的。

5 結語

通過公式推導，可以得出方變圓幾何體的體積公式為：

這也從拆解變形法中得到了驗證，從而證明了該式的正確性。

[1]DL/T5145－2002，火力發電廠制粉系統設計計算技術規定[S]．

[2]原北京礦業學院高等數學教研組．數學手冊[M]北京：煤炭工業出版社，1976．