一種適用于深海長基線定位的自適應分層聲線跟蹤法

李圣雪，王振杰，聶志喜，王毅，吳紹玉

（1.中國石油大學（華東），山東 青島 266580；2.中國石油東方地球物理公司，河北 涿州 072751）

聲波在海水中的傳播方向會隨著聲速的變化而變化從而產生折射，這導致聲線軌跡不再是一條直線（趙建虎等，2008；孫革，2007）。如果采用固定的聲速計算，會帶來很大的誤差（齊娜等，2003）。為了提高精度，需要對聲線軌跡進行修正（王燕等，2009）。因此聲線跟蹤技術（何高文，2000；朱小辰，2011；蔡艷輝，2013）被應用到水聲定位領域。聲線跟蹤技術利用分層近似、逐層計算的方法對聲線彎曲進行補償，從而改善定位精度（張居成，2013；Yang et al，2011）。分層等梯度的聲線跟蹤方法是常用的一種聲線修正方法（劉伯勝，1997；Takahashi et al，2000），該方法假設層間聲速等梯度變化，采用逐層計算獲取的聲線軌跡與真實聲線軌跡最為接近，精度較高（葛亮，2006）。但在深海區域運用此方法定位時，定位效率會因為聲速層數過多而大大下降。本文提出了聲速剖面（李勝全，2001） 的自適應分層方法，將梯度變化較小的層進行合并，保留梯度變化較大的聲速層，減少迭代計算層數，在保證精度的情況下顯著地提高了運算速度。本文方法與張居成（2013）方法相比，原理更為簡單，實現更為方便。

1 分層等梯度聲線修正法

聲波在海水中的傳播遵循Snell 法則（張紅梅，2010；丁繼勝，2005）

式中：θ 為聲線入射角，C 為聲速，P 為Snell 常數。

分層等梯度聲線跟蹤方法假設聲波經歷的水柱分為N 個等梯度層，即聲波在每層的傳播速度是等梯度的。在水深為zi的i 層，分別用Ci和θi表示聲波的傳播速度和入射角度（圖1）。第i 層內的聲速梯度gi可用下式表示

式中：Δzi為第層的水層厚度，Ci+1為第i+1 層聲速。

由于聲波的傳播滿足Snell 法則，在聲速常梯度變化的情況下，波束在第i 層內的實際傳播軌跡為一連續的、對應一定曲率半徑Ri的弧段（陸秀平，2012；趙建虎，2002），Ri的表達式如下

層i 內聲線的水平位移（蘭華林，2007）為

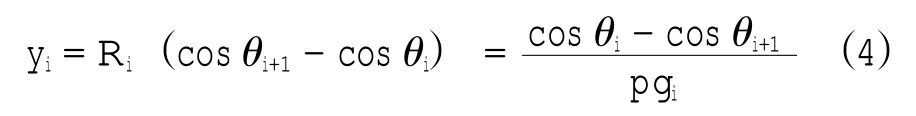
式中：θi為第i 層聲線的入射角，θi+1為第i+1 層聲線的入射角。

波束在該層經歷的弧段長度為

則經歷該段的時間為

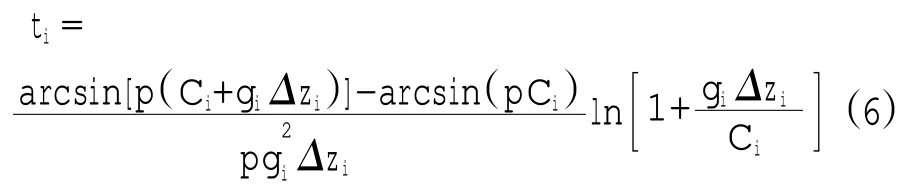
此種方法跟蹤的聲線路徑與真實聲線吻合，計算精度相對較高，但當數據層數較多時，迭代耗時，運算量大。

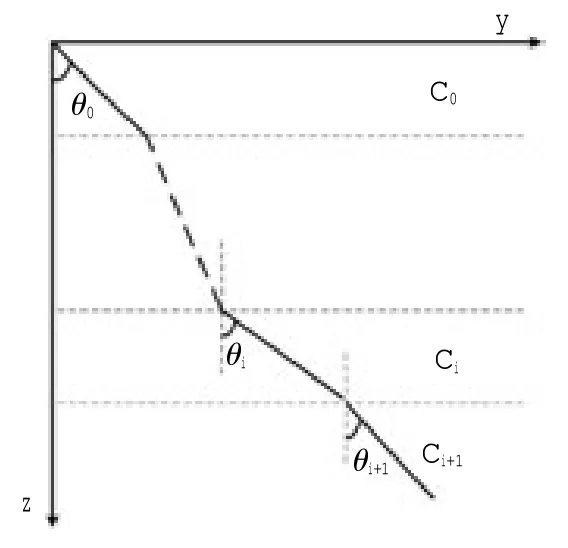
圖1 分層等梯度聲線跟蹤示意圖

2 自適應分層聲線跟蹤法

為了解決深海高精度定位運算量過大、定位效率低的問題，提出了自適應分層聲線跟蹤的方法。該方法的思想是通過對聲速剖面數據進行合理抽稀并保留信息量多的聲速層，在滿足定位精度需求的前提下減少定位耗時。聲速剖面自適應分層原理如圖2 所示。

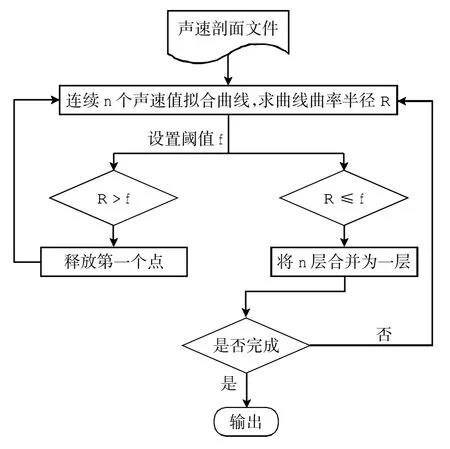
圖2 自適應分層原理圖

首先，設定合理的擬合窗口大小n，n 值取值過小會造成擬合多項式的參數不準確，n 值取值過大會造成擬合后層數過少。然后，從頂層開始選取連續的n 個聲速值Ci（i=1，2，…，n）進行曲線擬合。對于擬合的曲線求其最大曲率，曲率計算公式為

如果曲率小于等于設定的閾值，則將此n 層聲速值合并為一層；如果曲率大于設定的閾值（表明此數據中聲速剖面變化較大），則此n 層不能合并為一層，釋放n 個點中的第一個點，下移一個點繼續選取n 個點聲速值進行擬合。通過此方法將聲速剖面數據中變化很小的聲速層進行過濾，適當抽稀，保留聲速梯度變化較大的數據層，從而減少迭代中的運算量。

聲速剖面經過自適應分層后，用新的聲速剖面進行分層等梯度聲線跟蹤，從而完成水下定位解算。

3 仿真算例及結果分析

圖3 水域聲速剖面圖

根據聲速剖面數據（如圖3 所示，其中（a）數據為中國南海聲速剖面數據（Yang et al，2011），（b）為中國Argo 浮標數據（中國Argo 網站））進行浮標位置及聲波傳播時間數據模擬。利用自適應分層的聲速剖面將模擬的浮標定位數據進行解算，計算水下應答器的位置。定位模型為圓曲線模型，解算的方法為王燕等（2002）的分層等梯度聲線修正方法，坐標滿足要求時可結束迭代，獲取水下應答器的位置信息。將獲得應答器坐標與模擬坐標真值進行比對，求得真誤差，檢驗自適應分層聲線跟蹤方法的效果。

3.1 仿真算例1-500 m 水深實驗

如圖4，模擬4 個浮標布設成正方形形狀，邊長為1 600 m，給浮標的三維坐標分別加上2 m 的余弦波動。海底模擬4 個應答器A、B、C、D，坐標分別為（0，0，-500）、 （0，40，-500）、（40，0，-500）、（40，40，-500），單位均為m。總共模擬100 個歷元，浮標100 歷元位置放大如圖5 所示。水域的聲速剖面圖如圖3（a），采樣間隔為1 m。誤差模擬如下：換能器定位中誤差x、y、z 方向各10 cm，應答器時延偏差為8 cm 的系統誤差，測量時間造成10 cm 的測距中誤差。

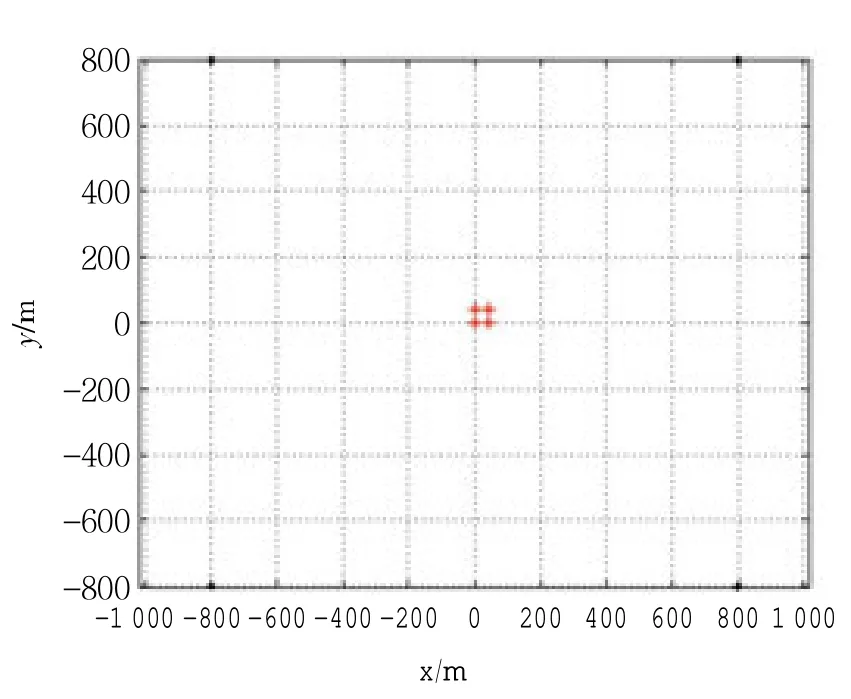
圖4 數據模擬示意圖

圖5 浮標100 歷元位置示意圖

為了進行對比，首先用原始聲速剖面（500層）對水下4 個應答器進行定位，4 個應答器定位結果見表1：

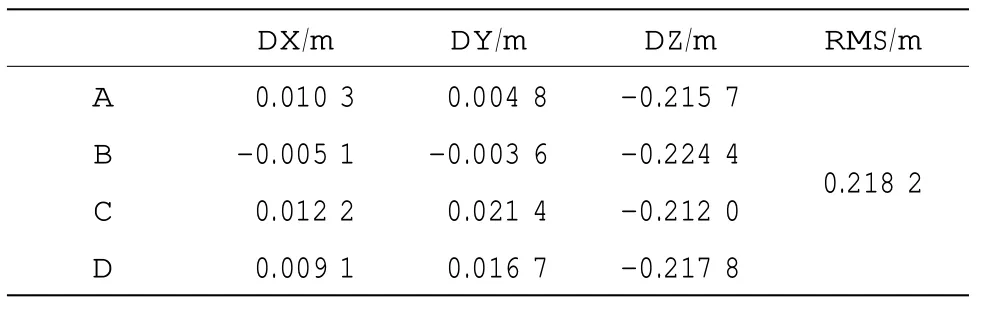
表1 500 m 數據分層等梯度聲線跟蹤定位誤差

實驗中的電腦配置為：CPU 型號為雙核Pentium E2200，CPU 主頻為2.20 GHz，內存大小為3G。用原始的聲速剖面定位，需要26.742 s，從表1 可以看出，水平方向的定位誤差最大為2 cm，最小為4 mm，定位精度為毫米級到厘米級，垂直方向的定位誤差在20 cm 左右，定位精度為分米級，RMS 值為0.218 2 m。

對聲速剖面進行自適應分層，為了測試閾值對定位結果的影響，實驗中閾值選取為10-1，10-2，10-3……，10-20，共20 個閾值，擬合點數n 設置為7，擬合曲線設置為三次多項式擬合，即每7 個數據點進行三次多項式擬合。

圖6 所示閾值為10-1與10-20時聲速剖面分層結果對比圖，可以看出閾值越大，層數越少。對于原始數據，均能進行不同程度的抽稀。

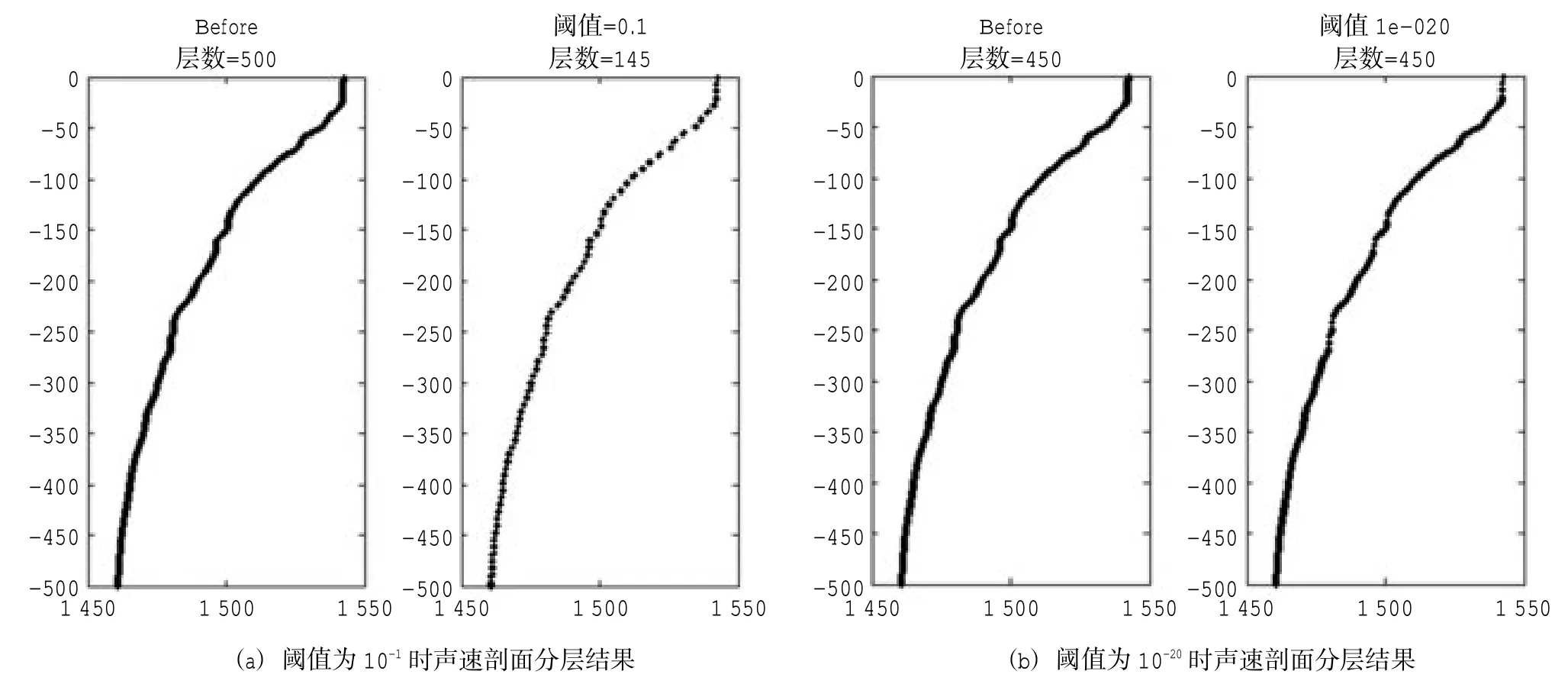
圖6 不同閾值時聲速剖面分層結果圖

利用上述11 個閾值得到的自適應分層聲速剖面數據進行分層等梯度聲線跟蹤定位水下4 個應答器的位置，計算結果見表2：

從表2 結果中可以看出，不同的閾值，對聲速剖面有不同程度的抽稀，層數從145 層到450 層，其中，閾值從10-1到10-12分層結果一致，均為145 層。定位的時間從不到7 s 到近24 s，定位的效率較原始結果有了不同幅度的提升。定位的精度方面：平面位置定位結果差別很小，誤差最大在2cm左右，最小不足4 mm。高程定位誤差在20 cm 左右，與原始定位誤差接近，不同閾值定位誤差差異很小。對于不同的閾值，其定位RMS 值均在0.22左右，相差不大，與未經過自適應分層的定位結果相當。圖7 為對于不同閾值的自適應分層定位結果水平方向RMS 和垂直方向RMS 的對比結果，可以看出不同閾值定位結果水平方向RMS 基本一致，垂直方向RMS 值區別不大，差別為毫米級。

3.2 仿真算例2-1 000 m 水深實驗

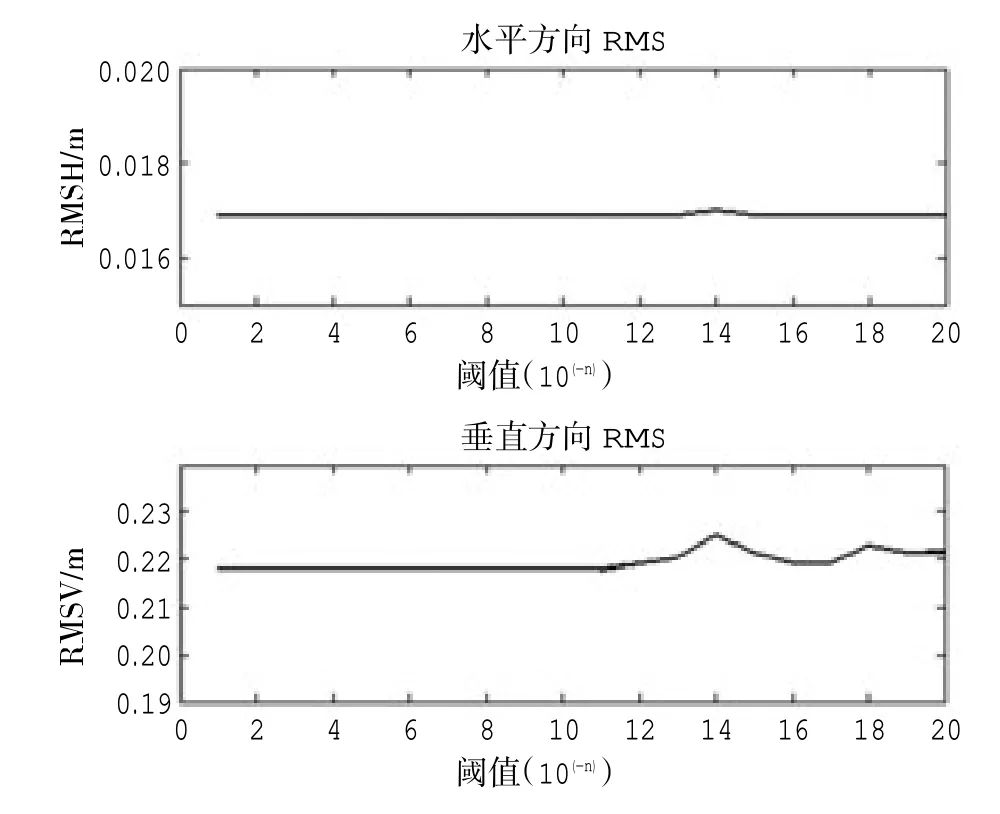
圖7 500 m 仿真數據不同閾值定位結果水平方向RMS 和垂直方向RMS 對比

模擬4 個浮標布設成正方形形狀，邊長為2 400 m，給浮標的三維坐標分別加上2 m 的余弦波動。海底模擬4 個應答器A、B、C、D，坐標分別為（0，0，-1 000）、（0，100，-1 000）、（100，0，-1 000）、（100，100，-1 000），單位均為m。總共模擬100 個歷元，水域的聲速剖面圖如圖3（b），采樣間隔為1 m。誤差模擬如下：換能器定位中誤差x、y、z 方向各10 cm，應答器時延偏差為8 cm 的系統誤差，測量時間造成10 cm 的測距中誤差。

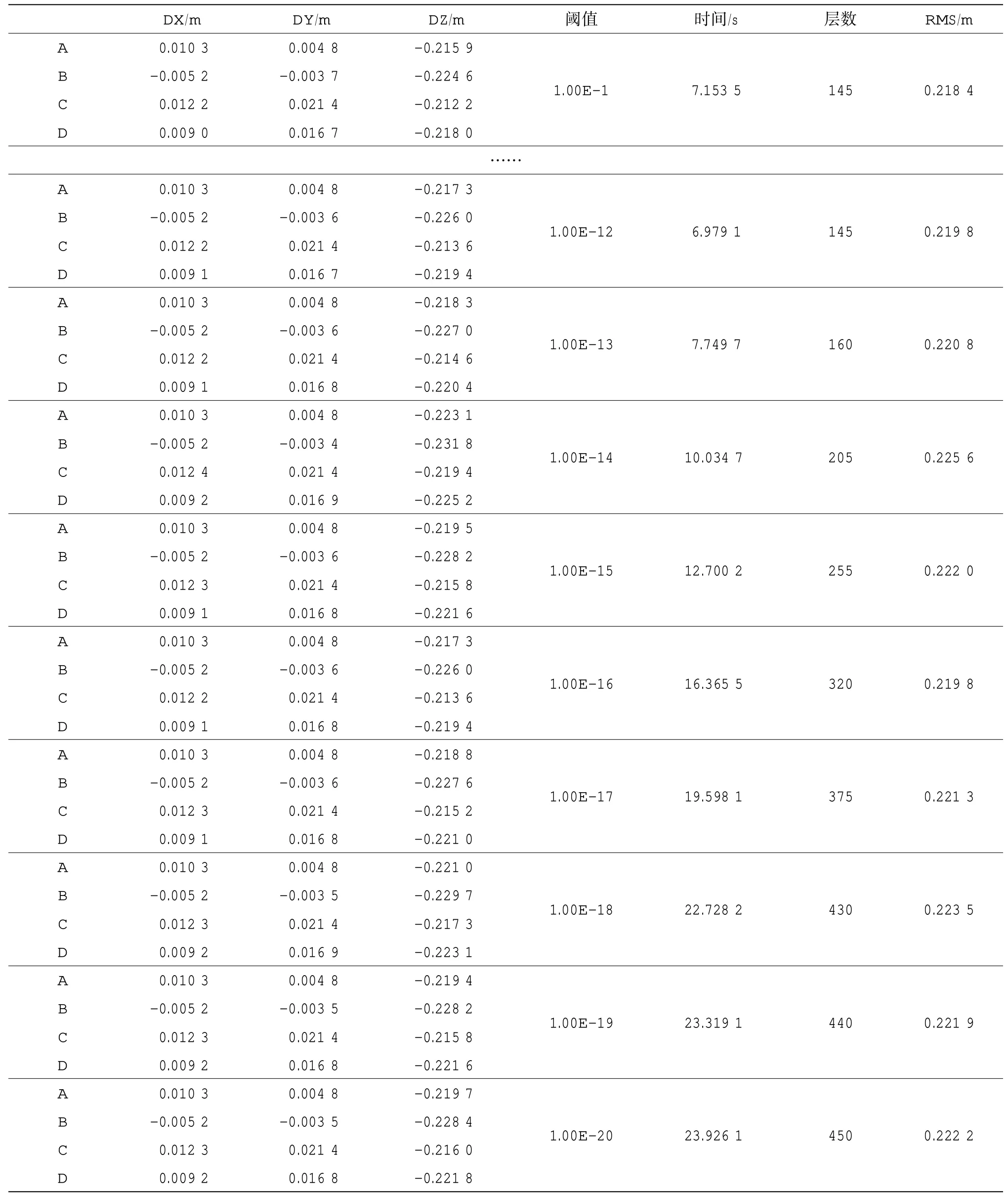
表2 500 m 仿真數據不同閾值水下定位誤差

首先，用原始聲速剖面（1 000 層）對水下應答器位置進行定位，結果如表3：

用原始的聲速剖面定位，需要的計算時間為41.272 5 s，從表3 結果可以看出，水平方向的定位誤差最大為2.26 cm，最小為3.7 mm，定位精度為毫米級到厘米級，垂直方向的定位誤差少于20cm，定位精度為分米級，定位的RMS 值為0.180 1 m。

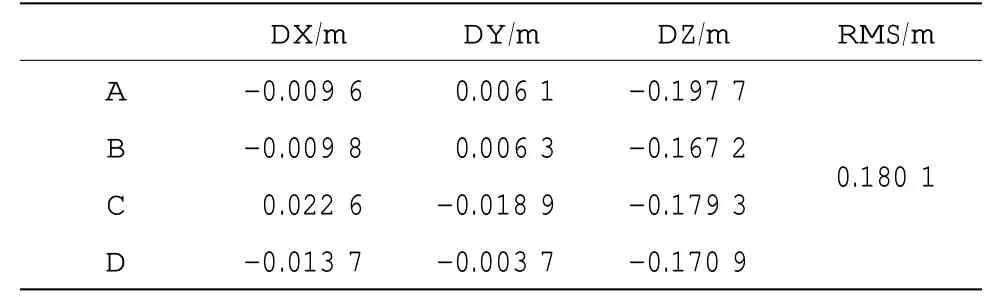
表3 1 000 m 數據分層等梯度聲線跟蹤定位誤差

利用新提出的自適應分層聲線跟蹤方法對水下應答器進行定位，20 個閾值定位結果如（下頁）表4：

從表4 中看出聲速剖面經過自適應分層后變化為從285 到730 層不等，閾值從10-1到10-10分層結果一樣，均為285 層。定位時間也從10 s 到34 s不等，定位的誤差與用原始聲速剖面定位的誤差相當，水平位置誤差最大不超過3 cm，最小不到2 mm，高程方向誤差基本不超過20 cm。對不同的閾值，定位RMS 值差別不大，與未經過自適應分層的定位結果相當。

圖8 為對于不同閾值的自適應分層定位結果水平方向RMS 和垂直方向RMS 的對比結果，可以看出不同閾值定位結果水平方向RMS 基本一致，垂直方向RMS 值區別不大，差別為毫米級。

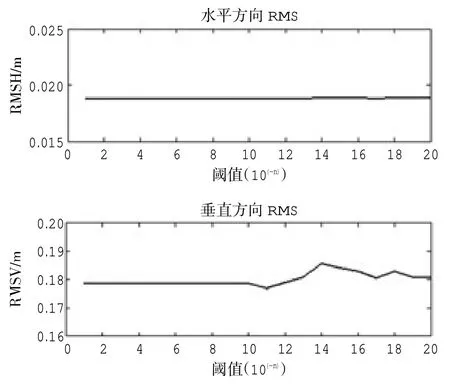
圖8 1 000 m 仿真數據不同閾值定位結果水平方向RMS 和垂直方向RMS 對比

從兩組實驗結果可以看出，對于不同的水深，不同的聲速剖面數據，提出的自適應分層聲線跟蹤方法均能有效地減少運行時間，在保證定位精度的前提下大大提高定位的效率。對比不同閾值的結果，在滿足需要的情況下可以設置較大閾值，保留主要信息層，提高定位效率。閾值的確定可以根據實際聲速剖面情況而定，試驗中可看出閾值為10-10即可滿足要求。

4 結論

本文針對提高深海聲學定位中分層等梯度聲線跟蹤定位的效率問題，提出了自適應分層聲線跟蹤的方法，得到如下結論：

（1）所研究的自適應分層聲線跟蹤方法可對聲速剖面數據進行合理分層，根據閾值大小保留必要的聲速層，在保證定位精度的前提下減少了迭代計算的時間，與傳統方法相比，明顯地提高定位效率，在深海水下導航定位中有較好的應用前景。

（2）分層閾值的選擇是一個值得研究的重要問題，本文采用的是實驗結果，關于閾值的自動選取方法還需要進一步深入研究。

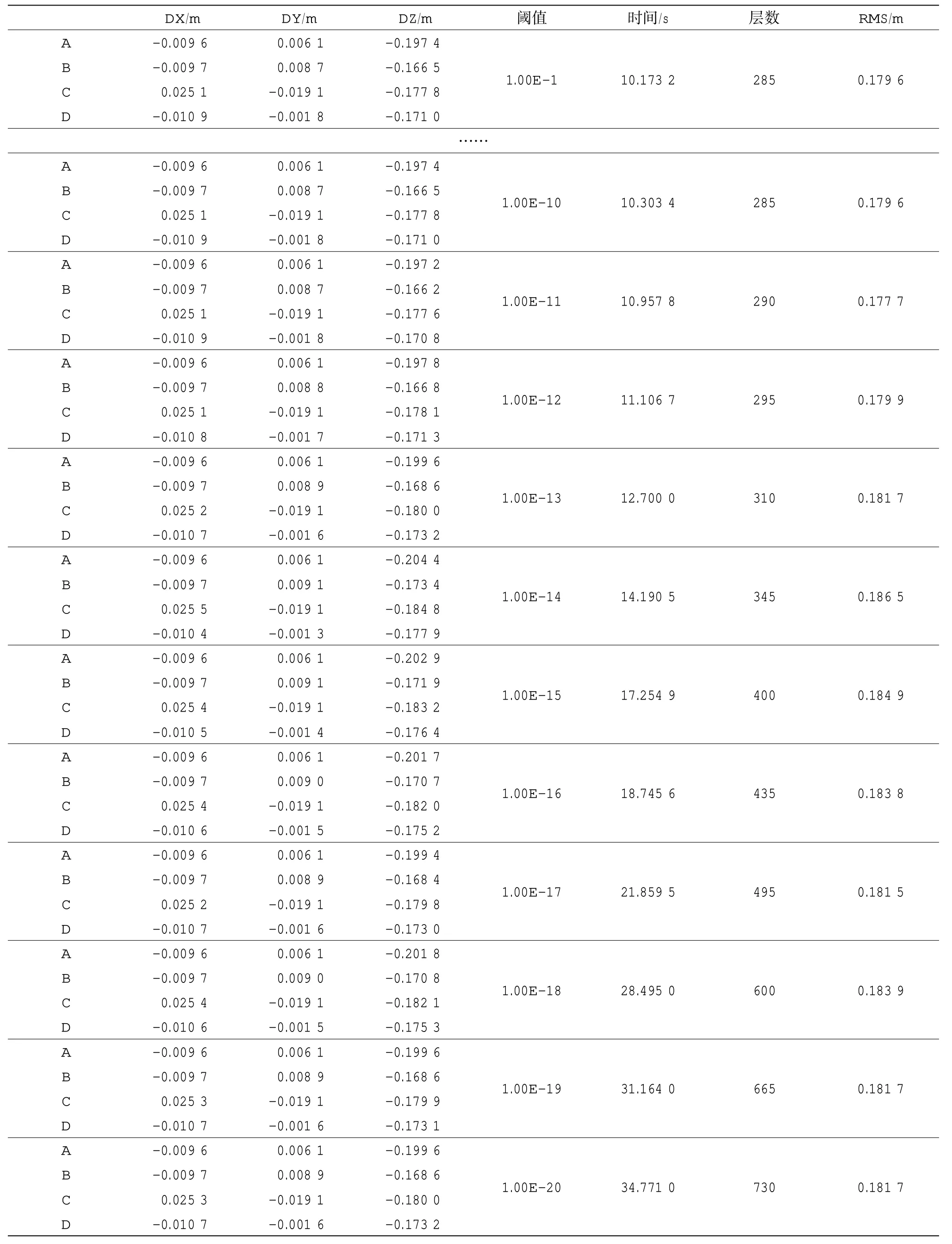
表4 1 000 m 仿真數據不同閾值的水下定位誤差

Takahashi N,Futa K,Tsuchiya T,et al,2000.Calculation of eigenray with equi-sound -speed division of sound speed profile. Acoustical Science and Technology,21(3):153-161.

Yang F, Lu X, Li J, et al, 2011. Precise positioning of underwater static objects without sound speed Profile. Marine Geodesy,34 (2): 138-151.

蔡艷輝，程鵬飛，2013.表層海水中聲納定位的聲速問題.遙感信息，（6）：3-9.

丁繼勝，周興華，唐秋華，等，2005.基于等效聲速剖面法的多波束測深系統聲線折射改正技術.海洋測繪，24（6）：27-29.

葛亮，2006.水聲定位技術在海洋工程中的應用研究初探.中國海洋大學.

何高文，劉方蘭，2000.多波束測深系統聲速校正.海洋地質與第四紀地質，20（4）：109-114.

蘭華林，2007.深海水聲應答器定位導航技術研究.哈爾濱工程大學.

李勝全，2001.聲速剖面測量.海洋測繪，4：28.

劉伯勝，雷家煜，1997.水聲學原理.哈爾濱：哈爾濱工程大學出版社.

陸秀平，邊少鋒，黃謨濤，等，2012.常梯度聲線跟蹤中平均聲速的改進算法.武漢大學學報信息科學版，37（5）：590-593.

齊娜，田坦，2003.多波束條帶測深中的聲線跟蹤技術.哈爾濱工程大學學報，24（3）：245-248.

孫革，2007.多波束測深系統聲速校正方法研究及其應用.中國海洋

大學.

王燕，梁國龍，2002.一種適用于長基線水聲定位系統的聲線修正方法.哈爾濱工程大學學報，23（5）：32-34.

王燕，林旺生，梁國龍，2009.聲線彎曲對同步水聲定位系統影響分析及修正.聲學技術，28（5）：123-124.

張紅梅，2010.水下導航定位技術.武漢：武漢大學出版社.

張居成，鄭翠娥，孫大軍，2013.用于聲線跟蹤定位的自適應分層方法.哈爾濱工程大學學報，34（12）：1-6.

趙建虎，2002.多波束測深及圖像數據處理方法研究.武漢大學.

趙建虎，劉經南，2008.多波束測深及圖像數據處理.武漢：武漢大學出版社.

朱小辰，劉雁春，肖付民，等，2011.海道測量多波束聲速改正精確模型研究.海洋測繪，31（001）：1-3.