波控中等潮差海灘剖面時空變化過程研究

于吉濤，丁圓婷，程璜鑫，陳子燊

（1.河南理工大學 測繪與國土信息工程學院，河南 焦作 454000；2.中國地質大學 環境學院，湖北 武漢 430074；3.中國地質大學 藝術與傳媒學院 湖北 武漢 430074；4.中山大學 地理科學與規劃學院，廣東 廣州 510275）

岬間海灘是全球岬角沉積海岸的一種重要地形，約占全球岸線的50%（Short et al，1999）。這些海灘在已有的文獻中有不同的名字，比如：ζ 彎曲海灘、半心型海灘、對數螺線海灘、鋸齒形海灘、彎狀或鉤狀海灘、袋狀海灘、岬間海灘和灣頭灘等（Yu et al，2011）。海灣特征是：一彎曲遮蔽段，一稍微彎曲的過渡段和下游一相對順直的切線段（如圖1）。這類海灘是在長期斜向盛行涌浪作用而形成，是海灣不同岸段波、潮、風等動力因子與海灘地形相互作用的結果，不同岸段的海灘剖面的物質組成、坡度和地貌形態的時空變化性一定程度上反映了復雜的海灘地形動力過程。本文通過對粵西水東灣——一波控中等潮差海灣切線段布設的一海灘剖面16 個月重復觀測獲取海灘剖面數據，通過經驗特征函數分析（EOF）剖面變化的主要空間特征及其物理意義，并對相對應的主要時間特征函數采用功率譜分析研究了主要剖面地形變化的時域特征。

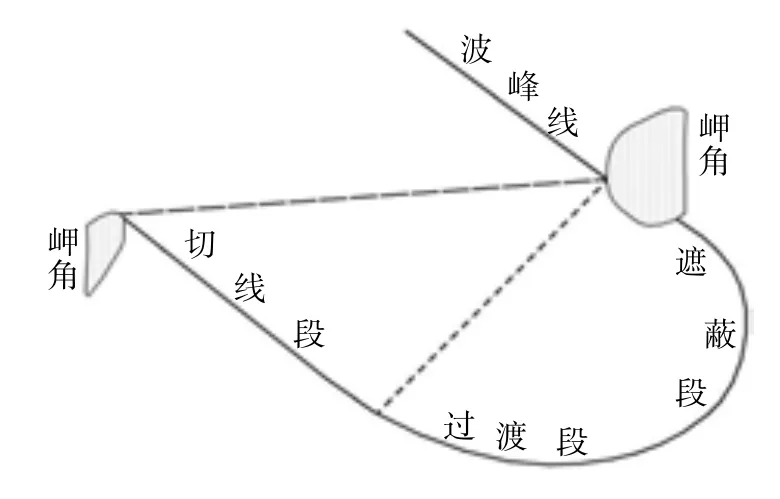
圖1 岬間海灘形態結構

1 研究區概況

研究區位于廣東省茂名市電白縣境內，海岸由沙壩—瀉湖—潮汐通道體系構成。沙壩長約9 km，走向大至呈北東—南西。沙壩分隔大海與瀉湖于南北兩面，留下一寬約1 km 的灣口成為瀉湖與外海之間的潮汐通道。由于水深很小的巨大落潮三角洲對入射波的消能作用以及具射流性質的落潮流對入射波的阻抗，使得落潮三角洲具有堆積性“岬角”性質。受這個“岬角”屏蔽和晏鏡嶺下岬角的控制，灣口以西岸線平面上也構成了頗具特色的岬間海灘。研究岸段屬于直線、開闊段，西接晏鏡嶺下岬角，東至晏鏡村，海灘長約2 km（圖2）。海灘高、中、低潮位附近表層泥沙由粗砂組成，平均粒徑分別為0.73 mm、0.59 mm 和0.63 mm，分選系數分別為0.49、0.63 和0.55，反映了高潮位和低潮位很好的分選、中潮位好的分選。研究區常浪向ESE，夏季多SE 向和SSE 向浪。潮汐屬于不正規半日潮類型，平均潮差1.75 m，平均大潮潮差2.6 m（陳子燊，2000）。按Davies（1964），研究區屬波控中等潮差海區。

圖2 研究區位置

2 數據預處理與研究方法

2.1 數據預處理

研究數據來自陳子燊（2000）數據，野外觀測期間該處海灘未受到人類活動干擾，基本處于自然狀態。對布設的這一條剖面，于每月大小潮期間進行測量，共獲得68 條實測海灘剖面高程數據，觀測時間16 個月。對每一條剖面水平距離等間隔分點（15 個高程點），得到相對于固定樁的距離（離岸距離）、絕對高程和海灘剖面圖；對原來不等時間步長的68 條剖面時序采用樣條函數以5d 等時序插值，得到96 條剖面（如圖3）。數據插值的主要目的是對EOF 分析得到的時間特征函數可進行譜分析，產生的譜的峰值可用于識別空間特征函數的周期性變化。

圖3 數據處理后96 條剖面形態圖

2.2 經驗正交函數

理解控制海灘時空變化的過程主要通過對海灘剖面連續數據包進行時空分解來實現，所采用的研究手段主要有經驗正交函數（Winant et al，1975；Aubrey，1978，1979；Losada et al，1991；Medina et al，1994；Pruszak，1993；Larson et al，1999；Mu?oz Pérez et al， 2001； Miller et al， 2007；Mu?oz Pérez et al，2010）或小波理論（Li Y et al，2005；Reeve et al，2007）。自從Winant 等（1975）和Aubrey（1978）定義了海灘變化后，經驗正交函數（Empirical Orthogonal Function，EOF） 方法已經被廣泛應用于海岸地貌研究中，主要應用于海灘的垂岸變化（Winant et al，1975；Aubrey，1978，1979；Losada et al，1991；Medina et al，1994；Pruszak，1993；Larson et al，1999；Mu?oz Pérez et al，2010） 和沿岸變化的研究（Mu?oz Pérez et al，2001；Miller et al，2007）。作為一種廣泛使用的統計工具，EOF 可被用于分析、確定海灘剖面隨時間或海灘位置的變化，它是一種壓縮型的研究剖面變化的方法，壓縮的數據可確定變化的相對重要程度。通過變量分離的方法將數據y（x，t）中的時間和空間相關性分開，數據可以被一系列時間和空間函數的線性組合來代表（Davis，1986；Jackson，1991；Miller et al，2007）：

其中，ek（x）為空間特征函數，ck（t）為時間特征函數或時間系數。通過k=1 到n 求和，n 是nx或nt中較小者，分別代表空間樣本數和時間樣本數。ak為標準化因子，（λk是第k 個特征函數的特征值），有時也會被并進ck（t）中。并要求特征函數滿足：

δmn為克羅內克δ，即確保得到的特征函數是由一組統計上相互獨立或不相關的向量所組成。特征函數以最小二乘法最優擬合數據，第一特征函數占據數據的大部分變化，隨后的特征函數占剩余變化的大部分。結果以數據可能的最緊湊的形式表示，確保前幾個特征函數占據最重要的變化。在數學上采用拉格朗日乘數法規范這一要求：

E 為空間特征函數矩陣，ek（x）和∧為特征值λk組成的三角矩陣。對矩陣A，本文采用交叉矩陣進行計算：

Y 是由y（x，t）的單獨要素組成，YT是Y 的轉置陣，方括號中的項代表矩陣A 的維數。當空間特征函數ek（x）被確定后，時間特征函數的求解可采用類似空間特征函數的計算步驟：

矩陣B 給出了y（x，t）時間協方差的測度，矩陣A 給出了y（x， t） 空間協方差的測度。如公式（5）和（6）所示，[nt，nt]為矩陣B 的維數，C 包含時間特征函數ck（t）。公式（4）和（6）的比較指示了矩陣A 和B 有不同的維數，因此二者方程中∧的計算也是不同的維數。

當給出矩陣A 和B 的定義，矩陣的跡或對角元素之和必須等于數據的均方值。方程（3） 和（5）也反映了矩陣的特征值之和必須等于數據的均方值，每一個單獨的特征值λk代表了模態k 占總變化的相對貢獻量，那么pk的計算為：

前幾個模態將包含數據中的大部分的變化量，即EOF 能把數據中有意義的主要信號與較低模態中的噪音區分開。而對于每一對聯合特征函數yk（x，t）=akck（t）ek（x），則可基于一個預設的水平L 重構原始數據。即：

通常基于方差閾值指定L，代表最小數量變化的模態被認為是噪音，可被濾除，即重構過程具有濾波功能。另外，由于單獨的ek（x）和ck（t）常常比較抽象，而yk（x，t）所代表的聯合特征函數由于更容易被理解，也是很有用的。

3 結果與討論

通過3.1 數據預處理得到96×15 剖面高程數據（圖3），分別計算這一數據的平均剖面、極差與標準差（圖4），然后對這一數據進行EOF 分析（圖5、圖6）。注意在對剖面高程數據做EOF 分析時，本文對這一數據進行了距平處理。如果沒有對數據去平均，第一空間特征函數e1（x）將明顯與統計平均值密切相關，將占剖面總變化的98.76%，指示的是平均海灘函數，這一結果已經被Winant 等（1975）和Miller 等（2007）所證實。本文通過對數據去平均，提取了占數據總方差91.32%的前3個空間特征函數來研究海灘剖面的空間變化（表1、圖5），并對相對應的前3 個時間特征函數（圖6）作連續功率譜估計及檢驗（圖7），以識別這一海灘剖面變化的時間特性。

表1 前4 個特征函數所代表的總變化（pk）的百分比

圖4 剖面的平均值、極差和標準差

圖4 所示的平均剖面從岸上向水下呈現出一個相對平穩的線性趨勢，極差與平均岸線趨勢相似，結合圖3 可看到平均水面位置有約10 m 的活動范圍，反映了潮汐水面對平均水平面的平移作用；標準差從岸線0 位置向離岸30 m 處，呈逐漸線性增加的趨勢，表明剖面變動逐漸加劇；離岸30 m 到50 m 處標準差呈線性減小的趨勢，表明剖面變動相對前一位置逐漸減弱；離岸50～70 m 處標準差又呈線性增加的趨勢，表明剖面變動進一步加劇。平均剖面、極差和標準差基本指示了該處海灘低潮帶附近及灘肩位置較強烈的剖面變動特征。

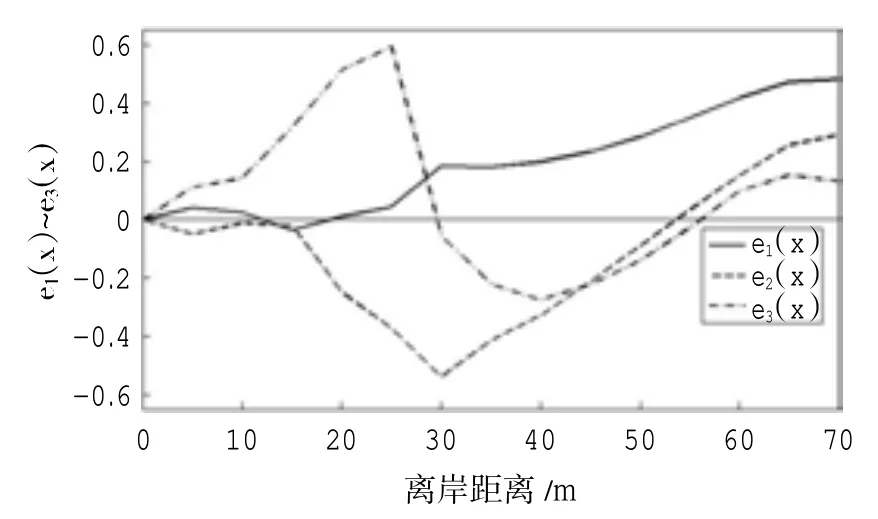
圖5 EOF 分析后得到的前3 個空間特征函數e1（x）- e3（x）

圖6 EOF 分析后得到的前3 個時間特征函數c1（t）-c3（t）

圖7 前3 個空間特征函數e（1x）-e（3x）對應的前三個時間特征函數c（1t）-c（3t）的各自功率譜

空間特征函數的極值表示最大變化的區域，而節點指示的是相對穩定的地帶，在節點處發生泥沙交換，可將毗鄰區域的淤積和侵蝕劃分開，因此剖面變化在結點兩側呈現反相。由圖5，第一空間特征函數e1（x）占總方差的49.85%，是海灘剖面變化最主要的模式。在離岸約12 m 和20 m 處存在節點，表明了該處泥沙的輸運，但是離岸0～25 m 的剖面變動相對穩定，指示了后濱相對穩定的特征；從離岸距離30～70 m 甚至更遠剖面變動逐漸增大，指示了灘肩頂至碎波帶海灘剖面變動逐漸增強的特征，反映了泥沙沿剖面的橫向往復運動，且沿著灘面向下泥沙變動逐漸增強，這是整個剖面形成和變化最主要的特征。從圖8 聯合特征函數圖中也可以看出，從離岸距離30～70 m 剖面的空間變化幅度為穩定的增加，體現了剖面變化的線性模式。對與第一空間特征函數e1（x）相對應的第一時間特征函數c1（t）（圖6）作連續功率譜分析，圖7（a）中的紅線代表置信水平95%的紅噪音理論檢驗譜，可發現第一時間特征函數的連續功率譜在波數16 處顯著，對應15 d 的顯著周期。反映了該海灘剖面波能在大、小潮汐約半月潮周期內對該過程的控制。這一從灘肩頂到中潮帶逐漸增加的狀態，表明了沿灘面向下的泥沙輸運是在第一個大潮間隔期間發生的。這時，沖流抵達，偶爾會越頂，灘肩頂處于連續的高潮下。當潮汐降為小潮時，海灘開始恢復，當經過下一個較低的大潮間隔時，泥沙被推回灘面。在下一個小潮間隔后隨著潮差增加到大潮，泥沙將沿灘面向下運動。這是最主要的海灘響應。

第二空間特征函數e2（x）占總方差的30.96%，是海灘剖面變動的次要模式。由圖5 可看出在離岸0～15 m 處剖面變動相對平穩，指示了相對穩定的后濱環境；自離岸15～30 m 處剖面變動逐漸增大，且在離岸30 m 出現極大負值，對應于灘肩向海端，在離岸約55 m 處出現結點，結點兩側呈反相，反映了高潮帶至上沖流作用上限之間剖面變動的主要特征，代表了灘肩的形成和消亡過程，是海灘剖面水上部分最主要的過程，為沖流帶函數模態，從圖8 聯合特征函數圖可更好的反映出灘肩的形成與消亡。對與第二空間特征函數e2（x）相對應的第二時間特征函數c2（t）作連續功率譜如圖圖7（b），可發現這一沖流函數模態的連續功率譜在波數10、11 處顯著，對應24～21.8 d 的顯著周期。這一沖流模態表明了沿著海灘的泥沙輸運有大約近塑望月潮頻率的周期。這一結果與Clarke 等（1984）的結果是一致的。隨著潮差的增加，剖面的上部將被沖流帶和碎波帶過程控制，較低的部分被波浪淺化過程所控制。實際上，高潮位以上灘肩地形的發展是和低潮位以下沙壩體系的動態密切相關的，若沙壩體系向岸遷移而且連接到灘面后，灘面坡度減小，海灘剖面為恢復粒級與波能之間的平衡關系，通過沖流過程，特別是高潮時的沖流作用把灘面泥沙向上搬運和堆積，此時波浪強度的波動又易使上沖泥沙越過灘肩脊堆積在灘肩頂面上，灘肩向上增長，并可能形成向岸傾斜的灘面連接面。隨著灘肩增長，灘面坡度增大，剖面將重新趨向平衡。

圖8 EOF 分析得到的前3 個聯合特征函數

第三空間特征函數e3（x）占總方差的10.51%，由圖5 可看出從離岸0～25 m 剖面變動逐漸加強，且在離岸25 m 處出現極大正值；在離岸30 m 出現結點，結點兩側反相，在離岸30～40 m，剖面變動又逐漸增強，且在離岸40 m 出現極大負值，但絕對值低于極大正值，在離岸55 m 附近出現結點，結點兩側反相。第三空間特征函數e3（x）主要體現了中潮帶上部灘面的波動特征，地形上對應于大潮高潮位的巨型灘角。Short（1991）提出，上漲的潮汐和入射波將相互作用而能是剖面維持，在高潮時將易于形成次諧邊緣波。長重力波的產生也將被上漲的、更高的潮汐所支持，但是，變化的水面可能將抑制它們對海灘下部地形的影響。在所有海灘系統中，高潮沖流帶可看到形成的灘角，存在中等到較高能量的大潮海灘系統中（Short，1991）。盡管對于灘角成因的研究有不同的看法，但野外觀測表明，這種高潮灘角的形成明顯地與大浪及大潮動力條件是聯系在一起的，由圖8 聯合特征函數圖可以直觀的顯示韻律地形的存在。對與第三空間特征函數e3（x）相對應的第三時間特征函數c3（t）作連續功率譜如圖圖7（c），可發現第三時間特征函數的連續功率譜在波數4、5、6 顯著，對應60～40 d 的顯著周期。反映了這一灘角地貌在大、小潮汐約2個月潮周期內對該過程的控制。

4 結論

本文通過對粵西水東灣——波控中等潮差海灘剖面數據進行研究，發現該段海灘整體表現出切線段海灘整體表現出低潮帶附近及灘肩位置較強烈的剖面變動特征，這一特征為平均海灘函數。通過EOF 分析，提取占矩陣總方差91.32%的前3 個空間特征函數研究海灘剖面空間變化，發現：（1）第一空間特征函數e1（x）占總方差的49.85%，是海灘剖面變化最主要的模式。指示了灘肩頂至碎波帶海灘剖面變動逐漸增強的特征，體現了海灘剖面的線性變化模式；（2）第二空間特征函數e2（x）占總方差的30.96%，指示了該處海灘灘肩的形成與消亡過程，這一特征為沖流帶函數模態；（3）第三空間特征函數e3（x）占總方差的10.51%，指示了韻律地形的存在，對應著大潮高潮位的巨型灘角地形。

通過對這3 個空間特征函數相對應的時間特征函數作連續功率譜分析，發現這3 個空間變化過程分別有約15 d、24～21.8 d、60～40 d 的周期，反映了該海灘剖面波能在大小潮汐約半月潮周期、近塑望月潮頻率周期和大小潮汐約2 個月潮周期內對這些空間過程的控制，體現了這一波控中等潮差海岸疊加在周期性潮汐之上的波浪作用使海灘演變的主要動力因素，這在以前的研究中（陳子燊等，1990；陳子燊等，1991；陳子燊，2000）所忽略。

Aubrey D G, 1978. Statistical and Dynamical Prediction of Changes in Natural Sand Beach,Ph D thesis，Scripps Institution of Oceanography,San Diego,194.

Aubrey D G, 1979. Seasonal Patterns of Onshore/Offshore Sediment Movement.Journal of Physical Research,84(C10):6347-6354.

Clarke D J,Eliot I G,Frew J R,1984.Variation in subaerial beach sediment volume on a small sandy beach over a monthly lunar tidal cycle.Marine Geology,58:319-344.

Davies J L, 1964. A morphogenetic approach to world shorelines.Zeitschrift für Geomorphologie,8:127-142.

Davis J C, 1986. Statistics and Data Analysis in Geology. John Wiley &Sons,Inc,New York,NY.

Jackson J E, 1991.A User's Guide to Principal Components. John Wiley&Sons,Inc,New York,NY.

Larson M, Hanson H, Kraus N C, et al, 1999. Short and long term responses of beach fills determined by EOF analysis. Journal of Waterway,Port,Coastal and Ocean Engineering,125(6):285-293.

Li Y,Lark M,Reeve D,2005.Multi-scale variability of beach profiles at Duck：A wavelet analysis.Coastal Engineering,52:1133-1153.

Losada M A, Medina R, Vidal C, et al, 1991. Historical evolution and morphological analysis of El Puntal spit,Santander (Spain).Journal of Coastal Research,7:711-722.

Medina R,Losada M A,Losada I J,et al,1994.Temporal and spatial relationship between sediment grain size and beach profile. Marine Geology,118:195-206.

Miller J K,Dean R G,2007.Shoreline variability via empirical orthogonal function analysis：Part 1 temporal and spatial characteristics.Coastal Engineering,54:111-113.

Mu?oz Pérez J J,Medina R, Tejedor B,2001.Determination of longshore variations by EOF method in Victoria Beach (SW Spain). Scientia Marina,65(4):393-402.

Mu?oz Pérez J J, Medina R, 2010. Comparison of long-, medium- and short-term variations of beach profiles with and without submerged geological control.Coastal Engineering,57:214-251.

Pruszak Z, 1993. The analysis of beach profile ch anges using Dean's method and Empirical Orthogonal Functions. Coastal Engineering,19:245-261.

Reeve D,Li Y,Lark M,Simonds D,2007.An investigation of the multiscale temporal variability of beach profiles at Duck using wavelet packet transforms.Coastal Engineering,54:401-415.

Short A D, 1991. Macro -Meso Tidal Beach Morphodynamics—An Overview.Journal of Coastal Research,7(2):417-436.

Short A D, Masselink G, 1999. Embayed and structurally controlled beaches.In：Short,A D （Ed.）,Handbook of Beach and Shoreface Morphodynamics.Wiley,New York,230-249.S

Winant C D, Inman D L, Nordstrom C E, 1975. Description of Seasonal Beach changes Using Empirical Eigenfunction.Journal of geophysical Research,80(15):1979-1986.

YU Ji-tao, CHEN Zi-shen, 2011. Study on Headland-Bay Sandy Coast Stability in South China Coasts.China Ocean Engineering,25(1):1-13.

陳子燊，李春初，1990.弧形海岸中間過渡帶海灘剖面的地貌動態分析.海洋科學，2：6-12.

陳子燊，李春初，羅章仁，1991.廣東水東灣弧形海岸切線段海灘剖面的過程分析.海洋學報，13（1）：82-90.

陳子燊，2000.海灘剖面時空變化過程分析.海洋通報，19（2）：42-48.