基于約束Delaunay三角網(wǎng)的線、面群目標(biāo)分布邊界計算
祿小敏,閆浩文,王中輝,甘治國
(1.蘭州交通大學(xué) 測繪與地理信息學(xué)院,甘肅 蘭州730070;2.甘肅省地理國情監(jiān)測工程實驗室,甘肅 蘭州 730070;3.中國水利水電科學(xué)研究院,北京100044)
群組目標(biāo)是由多個單目標(biāo)因局部空間關(guān)聯(lián)度高而形成的集合。在地理空間中,空間目標(biāo)在許多情況下都是以群組的形式出現(xiàn),如高程點、道路、河流、居民地、島嶼等。按照構(gòu)成要素的不同幾何屬性,群組目標(biāo)一般分為點群、線群與面群3類[1]。
群組目標(biāo)的分布邊界能夠很好地描述群組目標(biāo)的空間形態(tài)以及分布范圍,在空間方向關(guān)系判斷[2]、空間相似度計算[3]、地圖自動綜合[4]等領(lǐng)域有著重要的應(yīng)用。目前,有關(guān)群組目標(biāo)的分布邊界計算主要是針對空間點群目標(biāo),提出的代表性方法有“剝皮”法[5]、外圍點連接 法[6]、Voronoi圖法[7]等。相比而言,對于空間線、面群組目標(biāo)的分布邊界計算問題卻鮮有學(xué)者涉獵。
鑒于此,本文在約束Delaunay三角網(wǎng)的基礎(chǔ)上,通過設(shè)定動態(tài)閾值,利用“剝皮”法提出一種針對空間線、面群組目標(biāo)的分布邊界求解算法。
1 算法描述
1.1 算法的主要過程
群組目標(biāo)的分布邊界是指能夠準(zhǔn)確表達群組目標(biāo)空間形態(tài)和分布范圍的多邊形,如圖1中的多邊形abcdef a所示。

圖1 面群的邊界多邊形
根據(jù)Gestalt心理學(xué)的鄰近性原則,只有兩點相距小于視覺鄰近距離時,其連接才能充當(dāng)群組目標(biāo)的分布邊界[5]。眾所周知,Delaunay三角網(wǎng)是計算和分析空間鄰近性問題的優(yōu)秀工具[8]。因此,本文擬通過構(gòu)建線、面群的約束Delaunay三角網(wǎng),利用“剝皮”法刪除兩點距離大于視覺鄰近距離的三角形邊,得到線、面群的分布邊界多邊形。算法的主要過程如圖2所示。

圖2 算法的主要過程
1.2 數(shù)據(jù)結(jié)構(gòu)
本文算法中用到的數(shù)據(jù)結(jié)構(gòu)主要有邊數(shù)據(jù)結(jié)構(gòu)和三角形數(shù)據(jù)結(jié)構(gòu)。其中,邊數(shù)據(jù)結(jié)構(gòu)的核心參數(shù)是left Triangle,right Triangle,分別表示邊的左、右鄰接三角形索引;三角形數(shù)據(jù)結(jié)構(gòu)的核心參數(shù)是triangle A,triangle B,triangle C,分別表示三角形三個頂點A,B,C的對邊的鄰接三角形索引。
1.3 算法的詳細(xì)描述
本文以線群目標(biāo)為例介紹算法的詳細(xì)步驟。
1.3.1 線群的約束Delaunay三角剖分
下面結(jié)合圖3對線群的約束Delaunay三角剖分過程[9]進行描述。
Step 1 利用Watson算法 構(gòu)建線群特征點集的初始Delaunay三角網(wǎng)(見圖3(a)),并將三角網(wǎng)中所有的三角形存入三角形數(shù)組;
Step 2:線群特征邊入網(wǎng),具體方法如下:
1)在三角形數(shù)組中查找與線群的特征邊相交的所有三角形,并建立由這些三角形中和特征邊不相交的邊與該特征邊構(gòu)成的邊數(shù)組L,具體分兩種情況:若此特征邊恰好是三角形的一條邊,這種情況不做任何處理;否則,按照下述方法構(gòu)建邊數(shù)組:
①見圖3(a),從三角形數(shù)組中查找與線群特征邊LiLj相交且其頂點為Li的首三角形T1;
②將當(dāng)前三角形(如T1)中不與特征邊LiLj相交的邊ELi與LiA加入邊數(shù)組,同時查找與T1相鄰接且與LiLj相交的三角形T2,并從三角形數(shù)組中刪除T1;將T2作為當(dāng)前三角形,重復(fù)該過程,直到當(dāng)前三角形為末三角形T5為止,并將T5中與特征邊不相交的邊CLj與LjD加入到邊數(shù)組,同時從三角形數(shù)組中刪除T5;
③將LiLj加入到邊數(shù)組。
2)利用邊數(shù)組構(gòu)建特征邊LiLj的影響多邊形PL和PR,如圖3(b)所示,并將它們的頂點按逆時針方向存儲。
3)對影響多邊形進行Delaunay三角剖分(以PR 為例)[11],具體步驟如下:
①計算多邊形每個頂點的凹凸性;
②將多邊形頂點數(shù)組中的每個凸頂點(如圖3(c)中的頂點A)與其前后頂點Li,B組成△LiAB,若此三角形不包含多邊形的其它頂點,則將其保存到三角形數(shù)組中,并從多邊形頂點數(shù)組中刪除此凸頂點,重新計算受影響的頂點的凹凸性,重復(fù)該過程,直到多邊形頂點數(shù)組為空時結(jié)束;
③按最大-最小內(nèi)角準(zhǔn)則,對三角網(wǎng)進行LOP(Local Opti mization Procedure)優(yōu)化,結(jié)果如圖3(c)所示。
1.3.2 利用動態(tài)閾值“剝皮”法計算線群的分布邊界
“剝皮”即刪除那些位于Delaunay三角網(wǎng)外圍的非線群特征邊的邊長大于一定閾值的三角形。具體步驟如下:
Step1:設(shè)閾值d=k×Avelength,其中,k為“剝皮”等級(文中取k=2),Avelength為Delaunay三角網(wǎng)中各三角形邊長的平均值,d的值在每次“剝皮”后動態(tài)更新;

圖3 線群的約束Delaunay三角剖分
Step2:將線群的外圍非特征邊(即只有一個鄰接三角形的邊且其不是線群的特征邊)依次與閾值d比較,若邊長大于d,首先判斷刪除該邊后所在三角形的其他兩邊能否與其他邊構(gòu)成三角形,若能,將該邊刪除后轉(zhuǎn)Step3;否則保留該邊,重復(fù)此步驟;
Step3:將被刪除邊所在三角形的其余兩邊設(shè)置為外圍邊,重新計算Avelengt h并更新d值,逐層向內(nèi)侵蝕直到所有的外圍非特征邊邊長均小于當(dāng)前閾值d。
圖3(c)中的線群“剝皮”結(jié)果如圖4所示。

圖4 線群的"剝皮"結(jié)果
1.3.3 構(gòu)建線群的分布邊界多邊形
由于在“剝皮”之后,線群分布邊界的頂點是無序存放的,因此,需要將它們進行調(diào)整(本文采用逆時針方向存儲),從而構(gòu)建出最終的線群分布邊界多邊形。下面以圖5為例說明構(gòu)建分布邊界多邊形的具體方法。
Step1:在三角形數(shù)組中查找任意一條外圍邊(如圖5中的邊ab),將其端點加入到多邊形頂點數(shù)組。
Step2:將外圍邊ab的終點b作為起點查找多邊形的下一個頂點,具體過程為:
①在邊數(shù)組中查找以點b為起點的邊(如bj,bc),依次判斷它們是否為外圍邊,若是(如bc),則將其另一端點(如點c)加入到多邊形頂點數(shù)組;
②以點c為起點重復(fù)該過程,直至回到初始端點a。
按照上述方法,圖5中的多邊形頂點數(shù)組P={a,b,c,d,e,f,g,h,i,a}。

圖5 邊界多邊形的構(gòu)建
2 實驗與討論
本文借助Visual C++6.0平臺,編程實現(xiàn)上述算法,并以shape格式的線群(河系)、面群(居民地群)為例進行實驗,結(jié)果如圖6~圖9所示。其中,圖6、圖7是河系的分布邊界多邊形計算結(jié)果,圖8、圖9是居民地群的分布邊界多邊形計算結(jié)果。
群組目標(biāo)的分布邊界多邊形需符合人們的空間認(rèn)知習(xí)慣,為此,本文采用人群調(diào)查的方式對上述實驗結(jié)果進行驗證。其中,被調(diào)查者是50名具有不同專業(yè)背景的本科生,實驗要求被調(diào)查者對圖6~圖9中的線、面群分布邊界多邊形回答“好”、“較好”、“一般”和“不好”4個答案之一。表1是對應(yīng)的調(diào)查統(tǒng)計結(jié)果。
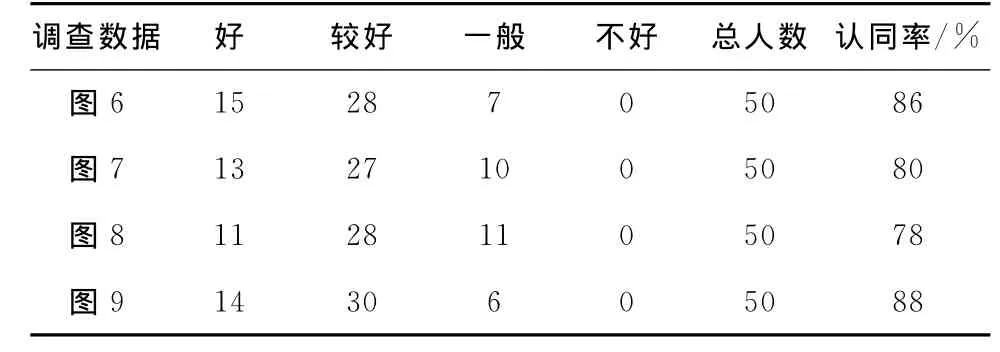
表1 人群調(diào)查統(tǒng)計表

圖6 實驗一
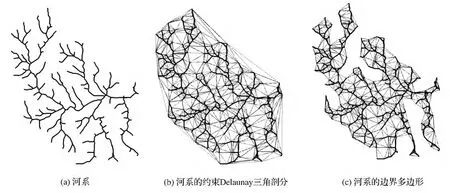
圖7 實驗二

圖8 實驗三
由表1可知,實驗結(jié)果的最高認(rèn)同率為88%,最低認(rèn)同率為78%,平均認(rèn)同率為83%,且認(rèn)為邊界多邊形描述群組目標(biāo)空間形態(tài)和分布范圍不好的人數(shù)均為0。這表明利用本文算法所求得的線、面群分布邊界多邊形符合人們的空間認(rèn)知習(xí)慣,較好地表達了空間線群、面群目標(biāo)的空間形態(tài)和分布范圍。
需要指出的是,剝皮的閾值d越大,剝皮的次數(shù)越少,得到的邊界多邊形越接近凸殼;d越小,剝皮的次數(shù)越多,得到的邊界多邊形就越接近線、面群的實際分布范圍。其中,閾值d中“剝皮”等級k的大小可在具體計算群組目標(biāo)的分布邊界時根據(jù)實際情況進行調(diào)整。

圖9 實驗四
3 結(jié) 論
本文在約束Delaunay三角網(wǎng)的基礎(chǔ)上,通過設(shè)定動態(tài)閾值,利用“剝皮”法實現(xiàn)空間線、面群組目標(biāo)的分布邊界求解。實驗表明,該算法能夠計算空間任意線、面群目標(biāo)的分布邊界多邊形,得到的結(jié)果符合人們的空間認(rèn)知習(xí)慣,較好地描述了線、面群目標(biāo)的空間形態(tài)和分布范圍。未來研究的重點是利用本文算法實現(xiàn)群組目標(biāo)的空間方向關(guān)系判斷和空間相似度計算。
[1] 劉濤.空間群組目標(biāo)相似關(guān)系及計算模型研究[D].武漢:武漢大學(xué),2011.
[2] 王中輝,閆浩文.基于方向Voronoi圖模型的群組目標(biāo)空間方向關(guān)系計算[J].武漢大學(xué)學(xué)報:信息科學(xué)版,2013,38(5):584-588.
[3] 劉濤,閆浩文.空間面群目標(biāo)幾何相似度計算模型[J].地球信息科學(xué)學(xué)報,2013,15(5):635-642.
[4] 閆浩文,王家耀.地圖群(組)目標(biāo)描述與自動綜合[M].北京:科學(xué)出版社,2009.
[5] 艾廷華,劉耀林.保持空間分布特征的群點化簡方法[J].測繪學(xué)報,2002,31(2):175-181.
[6] AHUJA N.Extraction of early perceptual str uct ure in dot patter ns:Integrating region,boundary and co mponent gestalt[J].Co mputer Vision,Graphics and Image Processing,1989,48(3):304-356.
[7] 李玉龍,朱華華.應(yīng)用Voronoi圖的點群范圍自動識別[J].工程圖學(xué)學(xué)報,2007(3):73-77.
[8] 姜志偉,王山東,王伶俐,等.基于格網(wǎng)和方向法索引的Delaunay三角網(wǎng)生成算法[J].測繪工程,2014,23(2):57-60.
[9] 王中輝,閆浩文.帶約束折線的平面散點集Delaunay三角剖分[J].測繪與空間地理信息,2011,34(1):46-47.
[10] WATSON DF.Co mputing the n-di mension Delaunay Tessellation with Application to Voronoi Polytopes[J].Co mputer Jour nal,1981,24(2):167-172.
[11]馬小虎,潘志庚,石教英.基于凹凸頂點判定的簡單多邊形Delaunay三角剖分[J].計算機輔助設(shè)計與圖形學(xué)學(xué)報,1999,11(1):1-3.

