考慮風電與用戶滿意度的電動汽車兩層智能充放電策略

黃貴鴻 雷 霞 楊 毅 王宇哲 陳曉盛

(電力電子節能技術與裝備重點實驗室(西華大學) 成都 610039)

?

考慮風電與用戶滿意度的電動汽車兩層智能充放電策略

黃貴鴻 雷 霞 楊 毅 王宇哲 陳曉盛

(電力電子節能技術與裝備重點實驗室(西華大學) 成都 610039)

大規模的電動汽車充放電調度問題既關系到電網的安全穩定運行，又關系到運營商的經濟利益和用戶的使用感受。引入分層分區調度的理念，構建了基于雙層規劃的電動汽車兩層智能充放電模型，并以IEEE16節點標準測試系統數據參數為基礎，通過粒子群算法和順序選擇法在Matlab中完成了仿真驗證。在上層模型中，通過優化各管轄區在各時段的總充放電功率，保證了運營商利潤的最大化，并合理地規避了充放電行為對電網的影響；在下層模型中，通過優化各管轄區內電動汽車的具體充放電策略，使得下層的調度策略與上層的區域總充放電功率盡可能保持一致，并合理地兼顧用戶滿意度。最后，通過上下層之間的數據交互，實現運營商、電網和用戶三者之間利益的有機協調。

電動汽車 分層分區調度 雙層規劃 粒子群算法 用戶滿意度

0 引言

隨著能源危機、環境污染和全球氣候變暖等趨勢的加劇，以電能這種清潔能源作為“燃料”的電動汽車擁有廣闊的市場前景[1-3]。然而在不久的將來，大量電動汽車接入電網，如果不對其充放電行為加以優化控制，必然會給現有電網的安全與穩定帶來嚴重影響[4-6]。

無論是在電動汽車的推廣階段還是普及階段，追求利潤的最大化都是運營商考慮得最多的問題，同時也是國內外學者研究的熱點問題[7-9]。文獻[8]以充電站運營收益最大化為目標，以配電變壓器容量及最大限度滿足用戶充電需求為約束條件，建立了充電站內電動汽車有序充電的數學模型；文獻[9]提出的有序充放電策略考慮了電動汽車充放電與風力發電在平抑負荷波動、減小峰谷差、降低網損等方面的互補效應；文獻[10]提出了一種電力市場環境下的電動汽車調度方法，通過選擇電價較低時段充電和向系統提供調頻或旋轉備用，以使電動汽車的總充電成本最小化；文獻[11]建立了以負荷峰谷差最小化為優化目標的計及用戶行駛習慣的插電式混合動力汽車智能充電模型，并對各時段PHEV的反向放電能力進行估算；文獻[12]根據電動汽車充電特性建立了電動汽車充電負荷模型，實現了平滑電網等效負荷波動的目的；文獻[13]提出了以換電站充電功率為控制對象的有序充電調度策略，有效減小了電網峰谷差，提高了負荷率，起到平穩負荷波動的作用；文獻[14]以電動公交車為研究對象分析其營運特點和充放電行為，同時在基于電池租賃的商業模式下，研究電動公交車的V2G放電能力，通過模擬集中充電站的運營情況，建立了集中充電、放電組合策略優化模型；文獻[15]引入了對電動汽車進行分層分區調度的理念，構建了基于雙層優化的可入網電動汽車充放電調度模型。在上層模型中，通過優化各電動汽車代理商在各時段的調度計劃，使系統在研究時間區間內總負荷水平的方差最小化，從而實現削峰填谷；在下層模型中，通過各電動汽車代理商對其所管轄電動汽車充放電時間的優化管理，以便與上層的調度計劃盡可能一致。

現有的電動汽車有序充放電策略僅考慮了問題的某一個方面，或僅從問題的某一個方面出發進行相對孤立的探討。首先，現有的有序充放電策略并未實現電網、運營商、用戶三者之間有機的協調；其次，現有的有序充放電策略并未充分利用電動汽車充放電與風力發電之間互補協調調度的經濟效應；最后，現有的有序充放電策略并未充分考慮到未來V2G的發展趨勢[16]。此外，在現有的有序充放電策略中，電動汽車運營商為了實現自身利益的最大化，可能會忽略用戶的滿意度。本文在現有的有序充電策略的基礎上，引入風力發電，提出了同時兼顧電動汽車運營商、電網和用戶利益的電動汽車智能充放電策略。

本文采用指定功率充放電模式，電動汽車具有額定的充放電功率，這決定了電動汽車充放電調度是一個離散的整數型優化問題。具體到每一輛電動汽車，充放電功率即額定充放電功率，不存在任何其他數值。運營商需要協調的，就是在一天中的24個時段內，各電動汽車最優的充放電時段。考慮到未來電動汽車用戶數量會呈現出顯著增長的趨勢，為了實現最優化調度，電動汽車運營商每天需要處理的數據量會非常龐大，如果依然采用現有的單層調度模式，無法實現決策的快速性和準確性。因此，本文提出了電動汽車兩層智能充放電策略，旨在實現電動汽車運營商利潤的最大化，保證現有城市配電網安全、穩定地運行，并盡可能地考慮到用戶的滿意度，最終保障電動汽車運營商持續、健康、穩定地運營。本文通過上層模型中的目標函數體現了運營商的利益，并通過約束條件，從安全性角度保證了電網的利益；在下層模型中，從用戶的行駛習慣和充/放電需求的角度，考慮了用戶的充放電滿意度；最后通過上下層交互，盡可能地使用戶的總體利益與運營商的利益在不斷博弈的過程中實現平衡，而在此過程中，電網的利益將始終得以滿足。

1 兩層優化調度模型

1.1 背景介紹

本文假設我國某個城市中的某電動汽車運營商共有M輛電動汽車需要調度，每一輛電動汽車都具有相同的電氣參數，即相同的額定容量、額定充/放電功率等，且嚴格服從電動汽車運營商的調度安排。現將電動汽車運營商所屬的M輛電動汽車根據電氣位置、地理位置等模糊特征進行歸類，并平均拆分為X個充電管轄區。這樣，每個充電管轄區內具有N輛電動汽車，計算量也隨之相應減小。

假設電動汽車運營商擁有自營的風電場，風機出力以預測值為準[17-20]，且通過獨立輸電線路直接服務于電動汽車用戶的充電。在一天中的某一個時段內，當用戶凈充放電總量(充電總量與放電總量之差)大于運營商自營風機出力時，運營商需要向電網購電；反之，運營商可向電網售電。無論是以上哪一種情況，電動汽車運營商均可通過與電網和與用戶之間的購售電價差實現盈利。

在此控制過程中，運營商在保證自身利益的同時，需要制定滿足電網安全性約束的各區域宏觀充放電功率。并在此基礎上，結合用戶的使用感受，制定具體到每個用戶(集群)的實際充放電調度功率。

1.2 控制流程

多層規劃概念最早是由J.Bracken和J.T.McGill[21]于1973年提出的，用以解決多層規劃與優化問題，其中雙層規劃是多層規劃的特例。顧名思義，雙層規劃包括上下兩層，上層決策結果一般會影響下層目標和約束條件，而下層則將決策結果反饋給上層，從而實現上下層決策的相互作用[15]。

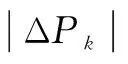
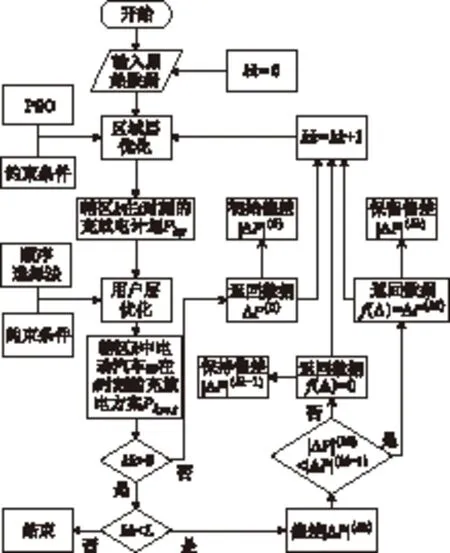
圖1 兩層優化控制流程Fig.1 Two-layer optimization control flow

2 區域層優化模型

2.1 目標函數

在區域層中，電動汽車充放電運營商以自身利潤最大化為控制目標，以不影響現有城市配電網安全運行為約束條件，通過粒子群智能優化算法，得到各充電管轄區在一天中24時段的最優區域總充放電功率Pk，t。區域層目標函數如式(1)所示。

(1)

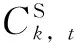
(2)

式(1)中，(Pk，t-βkPw，t)為考慮風機出力的電動汽車運營商旗下第k個充電管轄區在t時刻的對外總充放電功率。若Pk，t-βkPw，t>0，則表示該轄區所配給的風電額度不足以提供轄區內所用用戶的充電需求，此時運營商需要向電網購電；若Pk，t-βkPw，t<0，則表示該轄區所配給的風電額度足以提供轄區內所用用戶的充電需求，且還有結余，此時運營商可向電網售電。

2.2 風電單位折算成本

電動汽車運營商旗下擁有自營風力發電場，該風電場通過專用輸電導線與各充電管轄區相連。在本文中，風電場出力必須優先滿足用戶充電需要，若有剩余，可向電網反送電。假設風力發電機組使用壽命為20 a，考慮建設成本、維修費用、人力成本、物價上漲指數、政府補貼，電動汽車運營商自營風場的風電單位折算成本可通過式(3)得到[22，23]。

(3)

式中f(Y)可通過式(4)得到

f(Y)=(1+βCPI)Y-1[Cwage+(1+?m)Y-1Crepair]

(4)

式中，Cbuild為單臺風機建設成本；Nw為風機數量；βCPI為物價上漲系數；Cwage為年化人力成本；Crepair為年化維修成本；?m為風電場年化故障增長率；Bsubsidy為國家節能減排補貼。

2.3 約束條件

1)多時段潮流約束

(5)

且

(6)

式(5)、式(6)中

PEi,t=Pk,t-βkPw,t

(7)

式中，PDi，t、QDi，t分別為電動汽車、風機接入前，t時刻節點i接入的基礎負荷有功功率和無功功率；node表示節點總數；PEi，t為考慮風機出力的電動汽車運營商旗下第k個充電管轄區在t時刻的對外充放電功率，且轄區k與節點i相連；Ui，t為節點i在t時刻的電壓幅值；θij，t為節點i、j在t時刻的電壓相角差；Gij與Bij分別為連接節點i與j之間支路的電導和電納。

2)風電配額約束

(8)

3)風電機組出力約束

(9)

4)節點電壓偏移量約束

ΔUi,t≤5%

(10)

式中，ΔUi，t為節點i在t時刻的電壓偏移百分比。

5)線路潮流約束

(11)

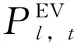
6)支路損耗約束

(12)

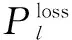
7)峰谷差約束

(13)

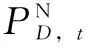
(14)

8)負荷率約束

(15)

9)負荷標準差約束

(16)

10)各充放電管轄區在時段t的調度約束

NkavPcharge≥Pk,t≥kSNkavPdischarge

(17)

式中，N為每個轄區所需調度的電動汽車數量；Pcharge為電動汽車額定充電功率；Pdischarge為電動汽車額定放電功率；kav為可用系數，由于所有電動汽車同時充電或同時放電的可能性幾乎為零，各轄區的實際總充放電功率必然小于該時段內電動汽車數量與額定充放電功率的乘積；kS為參與V2G的電動汽車數量占所有電動汽車總量的比值。

3 用戶層優化模型

3.1 目標函數

用戶層中，電動汽車充放電運營商以實際調度結果與區域層參考數據偏差的絕對值最小為目標，并充分考慮用戶的充放電需要，通過順序選擇法，得到每輛電動汽車的最優充放電策略。然后根據前面所提到的數據返回原則，選擇性地將實際調度結果與區域層參考數據的偏差返回到區域層。用戶層目標函數如式(18)所示。

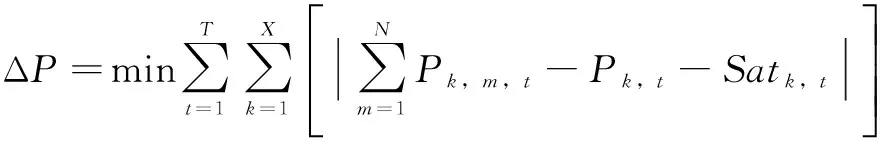
(18)

式中，Pk，m，t為轄區k中第m輛電動汽車在t時刻的充放電功率。每輛電動汽車都具有額定的充放電功率，當轄區m內第k輛電動汽車在t時刻充電時，Pk，m，t=Pcharge；當轄區m內第k輛電動汽車在t時刻放電時，Pk，m，t=Pdischarge。因此，用戶層控制變量Pk，m，t是一個只對時間t進行求解的一維未知變量；Satk，t表示用戶滿意度矩陣Sat第k行、第t列中的元素。滿意度矩陣Sat是描述用戶充放電行為的X×T維修正矩陣。

3.2 返回數據

本文將上下層最大交互次數設置為L，對于第kk次交互，若滿足返回數據的條件，則返回數據

(19)

即式(2)。因此，區域層目標函數(1)可改寫成如下形式

(20)

3.3 約束條件

1)電動汽車蓄電池充放電約束

(21)

式中，Sk，m，t為轄區k中第m輛電動汽車在t時刻的電池電量；ηch為充電效率；ηdch為放電效率。

2)蓄電池安全性約束

Smin≤Sk,m,t≤Smax

(22)

3)次日行駛需要約束

Sk,m,tk,m,d≥Srequire

(23)

式中，tk，m，d為轄區k中第m輛電動汽車的充電結束時間。

4)不可調度時段約束

Pk,m,t=0 (當ttk,m,d時)

(24)

式中，tk，m，a為轄區k中第m輛電動汽車的充電開始時間。

5)充/放電連續性約束

Pk,m,tk,m,a×Pk,m,tk,m,a+1×…×Pk,m,tk,m,d-1×Pk,m,tk,m,d≠0

(25)

且

Pk,m,tk,m,da×Pk,m,tk,m,da+1×…×Pk,m,tk,m,dd-1×Pk,m,tk,m,dd≠0

(26)

式中，tk，m，da為轄區k中第m輛電動汽車的放電開始時間；tk，m，dd為轄區k中第m輛電動汽車的放電結束時間。

6)不可同時充放電約束

tk,m,da≥tk,m,d+3

(27)

根據此約束條件，從充電結束時刻算起，電動汽車必須在2h后才能開始放電，既保證了電池的使用壽命，降低了使用成本，又符合常理。

4 仿真設置

4.1 基礎數據

本文是在IEEE16節點接線方式、線路參數等基礎上進行仿真的。圖2中，數字表示節點序號，帶“#”數字表示線路序號。三角形節點按升序分別接入電動汽車運營商旗下的第X個轄區。運營商自營風電場通過專用輸電線路直接與各充放電管轄區相連。

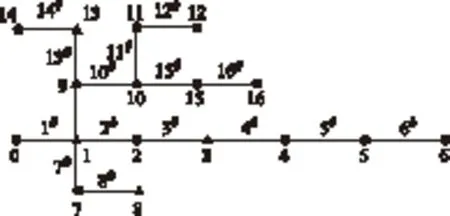
圖2 IEEE16節點接線圖Fig.2 IEEE16 node connection diagram

假設我國某個城市中的某電動汽車充放電運營商共有2 400輛電動汽車需要調度，該運營商旗下擁有6個充放電管轄區，每個充放電管轄區管轄400輛電動汽車的充放電行為。

為降低用戶層計算維度，提高計算速度，現將每個充電管轄區內的400輛電動汽車分為40個充放電集群，每個集群具有10輛充放電行為完全相同的電動汽車。這樣，計算維度也就從之前的400×24降低到40×24。

本文假設進行50次區域層與用戶層的數據交互。其中，區域層將向用戶層傳送51次基準數據，用戶層將向區域層返回50次修正數據。

運營商自營風電場風電機組出力值Pw，t直接引用了文獻[17-20]中的風電出力預測值。在一天中的24個時段，風電機組的出力如表1所示。

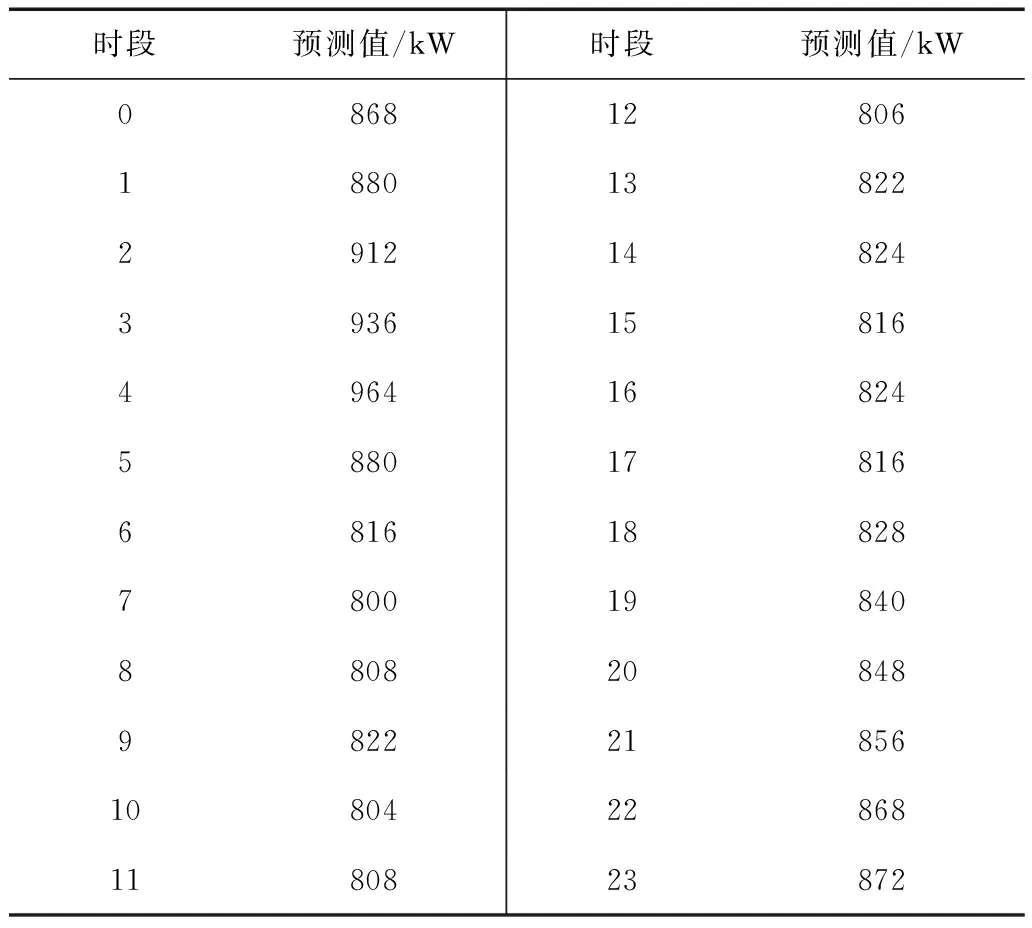
表1 風電機組出力預測值Tab.1 Predicted value of wind turbine operator set output

電動汽車運營商旗下6個充電管轄區所獲得的風電配額，可根據風機地理位置、輸電線路成本、配電網絡特性等實際情況進行適當選取。本文以6個充電管轄區分別獲得0.1、0.2、0.25、0.28、0.12和0.05的風電配額為例進行仿真計算。

本文仿真所采用的基礎負荷曲線直接引用了文獻[24-26]中的數據。在一天中的24個時段，基礎負荷如表2所示。

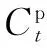
表2 基礎負荷Tab.2 Original load

文獻[26]中某地區高負荷率電價的基礎上，根據本文實際需要，做了適當修改。后者在低負荷率電價的基礎上[26]，根據本文實際需要，做了適當修改，制定了運營商與轄區一用戶之間的分時電價。其余充放電管轄區由于所處的地理位置、電氣位置不同，以轄區一為基準，電價有適當不同。其中，對于轄區二、三、四、五、六，運營商與用戶之間的電價在轄區一基準電價的基礎上，分別高出0.01、0.015、0.03、0.025和0.02元/kWh。運營商與電網之間的分時電價如表3所示。運營商與轄區一用戶之間的基準分時電價如表4所示。

表3 運營商與電網之間的分時電價Tab.3 Time-of-used electricity price between provider and grid

表4 運營商與轄區一用戶之間的分時電價Tab.4 Time-of-used electricity price between provider and users in district 1

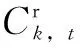
表5 轄區1單位運營維護成本Tab.5 Unit operation and maintenance cost in district 1

為簡化計算，本文將電動汽車運營商自營風電場風電單位成本Cw設置為0.35元/kWh。

4.2 充放電時間

假設每輛電動汽車具有相同的電池容量和充放電功率。其中，每輛電動汽車的電池容量為12 kWh，充電功率Pcharge為3 kW，放電功率Pdischarge為-1.5 kW。文獻[27，28]對電動汽車用戶的行駛習慣和充放電行為進行了建模分析，基于此，為保證第二天的正常使用，本文假設每輛電動汽車充電結束時的SOC(State of Capacity)滿足正態分布，其期望值為0.9；充電開始時的SOC亦滿足正態分布，其期望值為0.1。每輛電動汽車的充電效率ηch為80%，這樣，每輛電動汽車在一天中的連續充電時間TC滿足以4 h為期望值的正態分布，如式(28)所示。

(28)

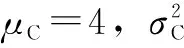
(29)

考慮到電動汽車具有參與放電的V2G行為，參與V2G的電動汽車占所有電動汽車總量的70%。假設參與V2G的電動汽車放電開始時的SOC滿足期望值為0.3的正態分布，放電效率ηdch為80%，這樣，每輛參與V2G的電動汽車在一天中的連續放電時間TD滿足以2 h為期望值的正態分布，如式(30)所示。

(30)

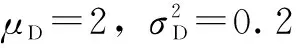
(31)

4.3 粒子群算法

在區域層中，本文采用粒子群智能優化算法進行求解[29]。其中，將優化變量Pk，t作為粒子，初始化粒子在式(17)的約束下隨機產生。初始化粒子個數設置為20，迭代次數設置為500。

粒子群算法計算流程：

1)初始化一群規模為20的粒子，每個粒子包括400×24維的隨機位置Pk，t和速度Vk，t。

2)評價每個粒子的適應度，即目標函數式(1)的值。

3)對每個粒子，將其適應度值與其目前取得的最好位置(局部最優值)對應的適應度值作比較，如果較好，則將此位置作為當前的局部最好位置pbest。

4)對每個粒子，將其適應度值與群體目前所取得的最好位置(全局最優值)對應的適應度值作比較，如果較好，則將該位置作為當前的全局最好位置gbest。

5)分別根據式(32)、式(33)調整粒子速度和位置。

Vk,t=w×Vk,t+c1×rand()×(pbestk.t-Pk,t)+

c2×rand()×(gbest-Pk,t)

(32)

Pk,t=Pk,t+Vk,t

(33)

6)迭代次數未達到500則轉向步驟2)。

4.4 考慮用戶滿意度的順序選擇法

在用戶層中，本文采用順序選擇法進行求解，得到每個電動汽車集群最優的充放電策略，進而得到Pk，m，t。以轄區一為例，通過區域層優化計算得到的區域總充放電功率P1，t具有最大值與最小值。現將P1，t最大值與最小值在一天中出現的最早位置t分別記為tmax和tmin，對于轄區一中的第一個電動汽車集群，將tmax作為其充電開始時間，將tmin作為其放電開始時間；修正P1，t，再一次將修正后的P1，t最大值與最小值在一天中出現的最早位置t分別記為tmax和tmin，對于轄區一中的第二個電動汽車集群，將tmax作為其充電開始時間，將tmin作為其放電開始時間；修正P1，t，以此往復，直到得到轄區一中所有電動汽車集群的充放電功率，進而得到所有電動汽車的充放電功率Pk，m，t。

考慮到用戶的實際充放電需要，絕大多數用戶希望在夜晚入睡時進行充電，此時的充電電價最低，如表4所示，同時充電也最方便。在文獻[27，28]對用戶行駛習慣和充放電需求進行建模分析的基礎上，本文對用戶的充放電行為進行了簡化。假設參與V2G的用戶均希望在下班回到家后的18∶00和19∶00開始放電，此時電動汽車處于閑置，電價處于峰時電價，獲利將會最大。這樣，考慮用戶滿意度后，根據順序選擇法的計算原理，可將用戶滿意度表示成6×24維矩陣Sat，并假設每個充放電管轄區內用戶滿意度指標相同，即Sat矩陣每行的行矢量相同。因此，可以將矩陣Sat的第k行以24維行矢量的形式表示成式(34)。

Satk=K[100,100,100,100,100,100,0,0,0,0,

0,0,0,0,0,0,0,-100,-100,0,80,80,80,80]

(34)

式中，K為用戶滿意度權重，K值越大，該充電策略越偏向于用戶的利益。第1列～第6列的數值為100，根據順序選擇法的計算原理，可在很大程度上將用戶的充電行為引入到00∶00～05∶00；第18列～第19列的數值為-100，可以在很大程度上將用戶的放電行為引入到17∶00～18∶00；第21列～第24列的數值為80，可在一定程度上將用戶的充電行為引入到20∶00～23∶00。在用戶層中采用順序選擇法進行求解時，可采用矩陣B取代之前的矩陣P(其第k行第t列元素為Pk，t)。矩陣B為區域層總充放電功率矩陣P與用戶滿意度矩陣Sat之和，即

B=P+Sat

(35)

對于每個充放電管轄區，依次通過順序選擇法，將得到其中每輛電動汽車的充放電策略Pk，m，t。用戶層求解最優調度方案的具體流程如圖3所示。

圖3 用戶層優化控制流程Fig.3 User-layer optimization control flow

5 仿真結果

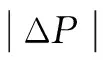
(36)

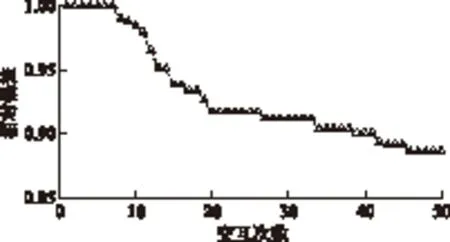
圖4 兩層優化相對偏差Fig.4 Two-layer optimization relative deviation

根據本文的構想，第46次交互所產生的區域層總充放電功率Pk，t和用戶層實際調度功率Pk，m，t即為最優的兩層調度方案。

在此最優調度方案下，可認為區域層與用戶層能夠協同調度，且區域層指標能相對準確地反應用戶層的相關指標。因此，以下均從區域層出發，探討在最優調度方案下，運營商利潤、電壓偏移量、線路潮流值、支路網損值、峰谷差、負荷率、標準差等指標。

在最優調度方案下，電動汽車運營商所取得的最大利潤為2.765萬元/d。以轄區一為例，區域層最優總充放電功率Pk，t如圖5所示。

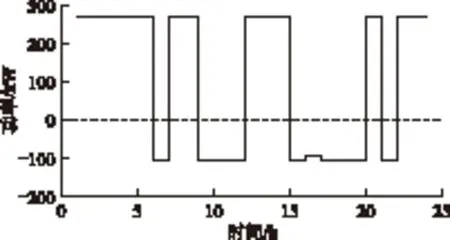
圖5 轄區一最優充放電計劃Fig.5 Optimumcharge-discharge plan for district 1

由圖5可知，充電管轄區對外所表現出的宏觀充放電行為符合實際需要，即在晚上進行充電，在下午負荷高峰且汽車閑置時段進行放電。該充放電計劃在為運營商賺取高額利潤的同時，在很大程度上提高了用戶滿意度，并合理地避開了負荷高峰。

以轄區一內各電動汽車集群為例，用戶層根據基準數據Pk，t得到的每個電動汽車集群充放電策略如表6所示。表6為一個40×24矩陣，表示轄區一內40個電動汽車集群在一天中24個時段的充放電策略。其中，第一列為行序數，表示電動汽車集群序列數；第一行為列序數，表示一天中的時段t。“+”表示充電，“-”表示放電，“空格”表示既不充電也不放電。根據本文假設，對于70%的電動汽車，既有充電計劃，也有放電計劃；對于30%的電動汽車，只有充電計劃，沒有放電計劃。

表6 轄區一各電動汽車集群充放電策略Tab.6 Charge-discharge tactics for every electric vehicle in district 1

以轄區一為例，區域層與用戶層的擬合程度如圖6所示。其中，光滑折線為圖5中的區域層最優區域總充放電功率Pk，t曲線，三角形折線表示用戶層在每個電動汽車集群均實現最優調度方案Pk，m，t的基礎上對外的總體表現，即

(37)

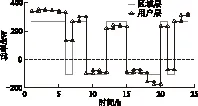
圖6 轄區一最優充放電計劃與調度方案Fig.6 Optimumcharge-discharge plan and scheduling scheme for district 1

由圖6可看出，在最優調度方案下，用戶層能很好地與區域層實現協同調度。由于考慮了用戶滿意度指標，在用戶層中，夜間總充電功率有所增大，18∶00、19∶00兩個時段總放電功率有所增大。

圖7表示電動汽車運營商在一天中24個時段內所管轄的所有電動汽車總充放電行為。

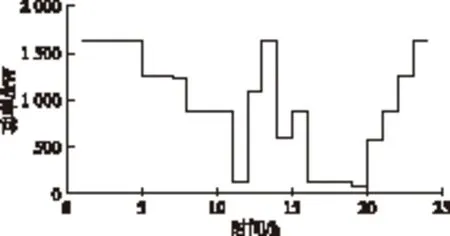
圖7 運營商總充放電曲線Fig.7 Gross charge-discharge curve for provider

由圖7中運營商總充放電曲線可看出，在任何時段，充電功率始終大于放電功率，因為對于電動汽車用戶而言，必然以充電為主，放電為輔。充電主要安排在負荷低谷時段，放電主要安排在負荷高峰時段。

在最優調度方案下，加入電動汽車和風機后的綜合負荷曲線與基礎負荷曲線如圖8所示。

由圖8可知，加入電動汽車和風電機組后，如果以本文提出的控制策略加以約束，負荷將會更加平穩，負荷曲線將會更加平滑。該控制策略無論在削峰填谷、平抑負荷波動還是在提高負荷率上，均有非常理想的效果。加入電動汽車和風電機組后的綜合負荷在峰谷差、負荷率和標準差上均明顯優于基礎負荷，且均滿足本文所設置的約束條件，其相關指標如表7所示。

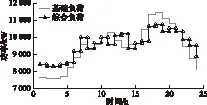
圖8 負荷曲線Fig.8 Load curve

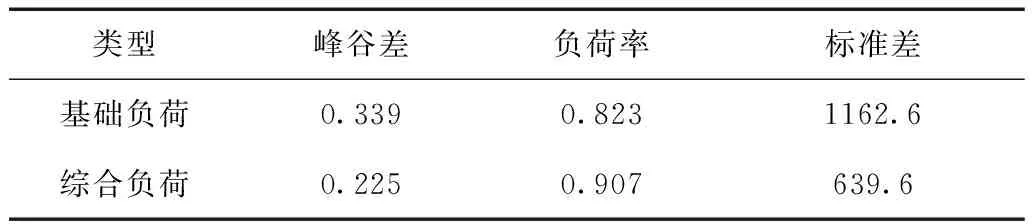
類型峰谷差負荷率標準差基礎負荷0.3390.8231162.6綜合負荷0.2250.907639.6

加入電動汽車與風電機組后，在18∶00和24∶00兩個典型時刻，節點電壓偏移情況如圖9所示。本文采用前推回代法計算節點電壓、網絡損耗和線路潮流[30]。

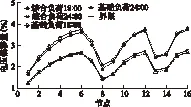
圖9 節點電壓Fig.9 Node voltage

加入電動汽車與風機后，在18∶00和24∶00兩個典型時刻，支路網損如圖10所示[30]。

圖10 支路網損Fig.10 Branch network loss

加入電動汽車與風機后，在18∶00和24∶00兩個典型時刻，線路潮流如圖11所示[30]。

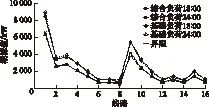
圖11 線路潮流Fig.11 Line power flow

由圖9～圖11可知，無論是在基礎負荷的最低谷時段，還是在基礎負荷的最高峰時段，電動汽車和風電機組的接入都未造成節點電壓、支路網損和線路潮流的越限。在基礎負荷的最低谷時段，隨著電動汽車和風機的接入，節點電壓、支路網損和線路潮流略有所增大；然而在基礎負荷的最高峰時段，隨著電動汽車和風機的接入，該指標卻有所減小。

本文并未考慮電動汽車充放電對配電網的諧波污染[31]。

6 結論

本文在分層分區的框架內，通過區域層與用戶層的智能交互，很好地實現了運營商、電網與用戶三者之間的有機統一。在運營商側，實現了運營商利潤的最大化；在電網側，保證了城市配電網的安全穩定運行，并在一定程度上提高了電能質量；在用戶側，通過引導充放電行為的方式，在一定程度上提升了用戶的滿意度。對電網而言，其利益是一個綜合、復雜和系統的問題，然而安全與穩定是電網運行的根本，因此本文主要考慮了電網的安全性約束；對電動汽車用戶而言，充放電成本是衡量滿意度高低的一個指標，然而充放電時段的合理性同樣重要，因此本文主要考慮了用戶的行駛習慣。運營商、電網與用戶三者之間的有機協調，依然是一個具有深入研究價值的課題。

[1] 張文亮，武斌，李武峰，等.我國純電動汽車的發展方向及能源供給模式的探討[J].電網技術，2009，33(4)：1-5. Zhang Wenliang，Wu Bin，Li Wufeng，et al.Discussion on development trend of battery electric vehicles in China and its energy supply mode[J].Power System Technology，2009，33(4)：1-5.

[2] Brooks A，Lu E，Reicher D，et al.Demand dispatch[J].IEEE Power and Energy Magazine，2010，8(3)：20-29.

[3] Andersen P H，Mathews J，Morten R.Integrating private transport into renewable energy policy：the strategy of creating intelligent recharging grids for electric vehicles[J].Energy Policy，2009，37(7)：2481-2486.

[4] Schneider K，Gerkensmeyer C，Kintner-Meyer M，et al.Impact assessment of plug-in hybrid vehicles on Pacific Northwest distribution systems[C].IEEE Power and Energy Society General Meeting on Conversion and Delivery of Electrical Energy in the 21st Century，Pittsburgh，PA，USA，2008：6.

[5] 馬玲玲，楊軍，付聰，等.電動汽車充放電對電網影響研究綜述[J].電力系統保護與控制，2013，41(3)：140-148. Ma Lingling，Yang Jun，Fu Cong，et al.Review on impact of electric car charging and discharging on power grid[J].Power System Protection and Control，2013，41(3)：140-148.

[6] 趙俊華，文福拴，楊愛民，等.電動汽車對電力系統的影響及其調度與控制問題[J].電力系統自動化，2011，35(14)：2-10. Zhao Junhua，Wen Fushuan，Yang Aimin，et al.Impacts of electric vehicles on power systems as well as the associated dispatching and control problem[J].Automation of Electric Power Systems，2011，35(14)：2-10.

[7] 趙俊華，文福拴，薛禹勝，等.計及電動汽車和風電出力不確定性的隨機經濟調度[J].電力系統自動化，2010，34(20)：22-29. Zhao Junhua，Wen Fushuan，Xue Yusheng，et al.Power system stochastic economic dispatch considering uncertain outputs from plug-in electric vehicles and wind generators[J].Automation of Electric Power Systems，2010，34(20)：22-29.

[8] 徐智威，胡澤春，宋永華，等.充電站內電動汽車有序充電策略[J].電力系統自動化，2012，36(11)：38-43. Xu Zhiwei，Hu Zechun，Song Yonghua，et al.Coordinated charging of plug-in electric vehicles in charging stations[J].Automation of Electric Power Systems，2012，36(11)：38-43.

[9] Song Yonghua，Yang Xia，Lu Zongxiang.Integration of plug-in hybrid and electric vehicles：experience from China[C].Proceedings of IEEE Power and Energy Society General Meeting，Minneapolis，MN，USA，2010：1-6.

[10]Caramanis M，Foster J M.Management of electric vehicle charging to mitigate renewable generation intermittency and distribution network congestion[C].Proceedings of the 48th IEEE Conference on Decision and Control，Shanghai，China，2009：4717-4722.

[11]李高望，錢斌，石東源，等.含插電式混合動力汽車的機組組合問題[J].電網技術，2013，37(1)：32-38. Li Gaowang，Qian Bin，Shi Dongyuan，et al.Unit commitment problem considering plug-in hybrid electric vehicle[J].Power System Technology，2013，37(1)：32-38.

[12]黃潤，周鑫，嚴正，等.計及電動汽車不確定性的有序充電調度策略[J].現代電力，2012，29(3)：57-63. Huang Run，Zhou Xin，Yan Zheng，et al.The controlled charging dispatch strategy by considering of the uncertainty of electric vehicles[J].Modern Electric Power，2012，29(3)：57-63.

[13]田文奇，和敬涵，姜久春，等.電動汽車換電站有序充電調度策略研究[J].電力系統保護與控制，2012，40(21)：114-119. Tian Wenqi，He Jinghan，Jiang Jiuchun，et al.Research on dispatching strategy for coordinated charging of electric vehicle battery swapping station[J].Power System Protection and Control，2012，40(21)：114-119.

[14]鄭丹，文福拴.租賃模式下的電動汽車電池集中充放電策略[J].華南理工大學學報(自然科學版)，2013，41(5)：105-111. Zheng Dan，Wen Fushuan.Charging and discharging strategies of batteries of electric vehicles in lease mode[J].Journal of South China University of Technology(Natural Science Edition)，2013，41(5)：105-111.

[15]姚偉鋒，趙俊華，文福拴，等.基于雙層優化的電動汽車充放電調度策略[J].電力系統自動化，2012，36(11)：30-37. Yao Weifeng，Zhao Junhua，Wen Fushuan，et al.A charging and discharging dispatching strategy for electric vehicles based on Bi-level optimization[J].Automation of Electric Power Systems，2012，36(11)：30-37.

[16]劉曉飛，張千帆，崔淑梅.電動汽車V2G技術綜述[J].電工技術學報，2012，27(2)：121-127. Liu Xiaofei，Zhang Qianfan，Cui Shumei.Review of electric vehicle V2G technology[J].Transactions of China Electrotechnical Society，2012，27(2)：121-127.

[17]劉瑞葉，黃磊.基于動態神經網絡的風電場輸出功率預測[J].電力系統自動化，2012，36(11)：19-22. Liu Ruiye，Huang Lei.Wind power forecasting based on dynamic neural networks[J].Automation of Electric Power Systems，2012，36(11)：19-22.

[18]Costa A，Crespo A，Navarro J，et al.A review on the young history of the wind power short-term prediction[J].Renewable and Sustainable Energy Reviews，2008，12(6)：1725-1744.

[19]楊秀媛，肖洋，陳樹勇.風電場風速和發電功率預測研究[J].中國電機工程學報，2005，25(11)：1-5. Yang Xiuyuan，Xiao Yang，Chen Shuyong.Wind speed and generated power forecasting in wind farm[J].Proceedings of the CSEE，2005，25(11)：1-5.

[20]葛江北，周明，李庚銀.大型風電場建模綜述[J].電力系統保護與控制，2013，41(17)：146-153. Ge Jiangbei，Zhou Ming，Li Gengyin.Review on large-scale wind farm modeling[J].Power System Protection and Control，2013，41(17)：146-153.

[21]Bracken J，McGill J T.Mathematical programs with optimization problems in theconstraints[J].Operations Research，1973，21(1)：37-44.

[22]徐麗萍，林俐.基于學習曲線的中國風力發電成本發展趨勢分析[J].電力科學與工程，2008，24(3)：1-4. Xu Liping，Lin Li.Study on the cost trends of wind power in china based on the learning curve[J].Electric Power Science and Engineering，2008，24(3)：1-4.

[23]周雙喜，王海超，陳壽孫.風力發電運行價值分析[J].電網技術，2006，30(14)：98-102. Zhou Shuangxi，Wang Haichao，Chen Shousun.Analysis on operation value of wind power resources[J].Power System Technology，2006，30(14)：98-102.

[24]趙儆，康重慶，葛睿，等.電力市場中多日負荷曲線的預測[J].電力自動化設備，2002，22(9)：31-33. Zhao Jing，Kang Chongqing，Ge Rui，et al.Multi-day load curve forecasting in electricity market[J].Electric Power Automation Equipment，2002，22(9)：31-33.

[25]肖建華，王銳鳳，溫春楠，等.典型日負荷曲線預測的一種簡單方法[J].吉林電力，2006，34(2)：14-17. Xiao Jianhua，Wang Ruifeng，Wen Chunnan，et al.A simple method of typical day load curve forecasting[J].Jilin Electric Power，2007，34(2)：14-17.

[26]郭聯哲，李莉，譚忠富，等.基于模糊需求和用戶分類響應程度的分時電價設計模型[J].華東電力，2007，35(5)：12-15. Guo Lianzhe，Li Li，Tan Zhongfu，et al.Time-of-use price design models based on fuzzy demand and users’diverse response[J].East China Electric Power，2007，35(5)：12-15.

[27]劉文霞，張敏，張建華，等.電動汽車負荷對配電網可靠性影響的量化分析[J].電力系統及其自動化學報，2013，25(4)：1-6. Liu Wenxia，Zhang Min，Zhang Jianhua，et al.Reliability modeling and quantitative analysis of distribution network considering electric vehicle charging and discharging[J].Proceedings of the CSU-EPSA，2013，25(4)：1-6.

[28]田立亭，史雙龍，賈卓.電動汽車充電功率需求的統計學建模方法[J].電網技術，2010，34(11)：126-130. Tian Liting，Shi Shuanlong，Jia Zhuo.A statistical model for charging power demand of electric vehicles[J].Power System Technology，2010，34(11)：126-130.

[29]李志，陳年生，郭小珊，等.粒子群算法及其改進技術研究[J].湖北師范學院學報(自然科學版)，2011，31(2)：104-108. Li Zhi，Chen Niansheng，Guo Xiaoshan，et al.Research on particle swarm algorithm and improved technology[J].Journal of Hubei Normal University(Natural Science Edition)，2011，31(2)：104-108.

[30]張立梅，唐巍.計及分布式電源的配電網前推回代潮流計算[J].電工技術學報，2010，25(8)：123-130. Zhang Limei，Tang Wei.Back/forward sweep power flow calculation method of distribution networks with DGs[J].Transactions of China Electrotechnical Society，2010，25(8)：123-130.

[31]張謙，韓維健，俞集輝，等.電動汽車充電站仿真模型及其對電網諧波影響[J].電工技術學報，2012，27(2)：159-164. Zhang Qian，Han Weijian，Yu Jihui，et al.Simulation model of electric vehicle charging station and the harmonic analysis on power grid[J].Transactions of China Electrotechnical Society，2012，27(2)：159-164.

Two-layer Smart Charge-Discharge Strategiesfor Electric Vehicles Considering Wind Generation and Users’ Satisfaction

HuangGuihongLeiXiaYangYiWangYuzheChenXiaosheng

(Key Laboratory of Power Electronic Energy-saving Technology & Equipment(Xihua University Chengdu 610039 China)

The charge-discharge dispatch problem for a large scale of electric vehicles is relevant not only to the electric grid’s secure and stable operation，but also to the providers’ economic profits and users’ feel.This paper creatively introduces the delaminating-partitioning scheduling concept and establishes a two-layer electric vehicle smart charge-discharge model.The particle swarm optimization (PSO) and the sequential selection methodare used to realize the bi-level programming simulation in MATLABto verify the modelthrough the IEEE16 node standard test system.In the upper-layer model，the maximization of the providers’ profit is ensuredthrough the gross charge-discharge power optimization to every partition at every time interval，and the effects of the charge-discharge activitieson the grid arereasonably evaded.In the lower-layer model，the target of the scheduling scheme is to satisfythe gross district charge-discharge power of the upper-layer model as far as possiblethrough optimization for the concrete charge-discharge strategiesof the electric vehicles in every district，and the users’ satisfaction is reasonably taken into consideration.At last，through the data interaction between the two layers，the coordination among the provider’s，grid’s and user’s interests are realized.

Electric vehicle，delaminating-partitioning scheduling，bi-level programming，particle swarm optimization，user’s satisfaction

2014-11-24 改稿日期2014-12-25

TM734

黃貴鴻 男，1988年生，碩士研究生，研究方向為新能源入網與電動汽車調度。(通信作者)

雷 霞 女，1973年生，教授，碩士生導師，研究方向為電力市場、調度自動化、配電自動化等。

四川省電力電子節能技術與裝備重點實驗室開放基金(szjj2014-015)和四川省教育廳重點項目(11za002)資助。