最小二乘配置在形變監測中的應用

郭迎鋼，李宗春，李 偉

(信息工程大學，河南 鄭州450001)

一、引 言

在變形監測過程中，要獲取監測區域變形情況的基本方法是在變形體的變形特征處設置一些監測點，通過重復觀測監測點的坐標來獲取區域的變形信息。在實際的監測過程中，如果對變形區域的某些沒有布設監測點的區域感興趣，雖然可以通過內插或擬合的方法來概略獲取其變形信息，但是無法進行精度評定。最小二乘配置具有可以評定精度的優點［1］，恰好能解決這個問題。

最小二乘配置起源于根據最小二乘推估來內插和外推重力異常的課題。1969年，經克拉魯普(T Krarup)的發展，提出了最小二乘配置法;莫里茲(H·Moritz)對最小二乘配置進行了系統深入的研究，提出了帶系統參數的最小二乘配置;經過以后的發展，最小二乘配置在大地測量、航空攝影測量、坐標系統變換、GPS水準擬合［2］、形變測量等方面得到了廣泛的應用［3］。本文將最小二乘配置應用于形變監測中變形網內插點的變形分析，并通過試驗對該方法的進行了驗證。

二、基于最小二乘配置的內差點形變分析

1．最小二乘配置原理

最小二乘配置的函數模型為

式中，L為維觀測向量;Δ為觀測誤差;X為t維非隨機參數;A為n×t階設計矩陣，rank(A)=t;Y為隨機參數，包括n維的已測點信號S和g維的未測點信號S'，所謂未測點信號，是指在觀測方程中不出現的信號。

最小二乘配置的隨機模型為

最小二乘配置的估值準則為

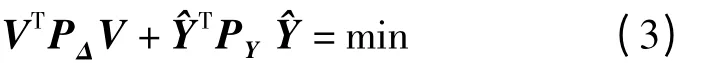
最小二乘配置的主要目的是估計未測點的完全信號

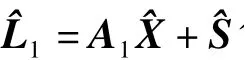
未測點完全信號的協方差矩陣如下

合理的協方差函數確定一直是最小二乘配置中的關鍵問題。在確定協方差函數時，一定要關注所研究對象的幾何和物理特性，因為這種特性決定了所研究對象內部的相關性，而如何正確反映這種相關性正是協方差函數一直追求的目標［4］，因此要具體情況具體分析，根據其特性選擇合適的方法［5］。

信號可以看作是平穩隨機過程的一個實現(觀測值)，可以用隨機過程的協方差函數來描述。常用經驗函數為

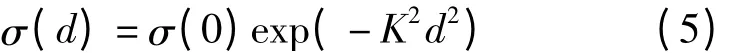
或

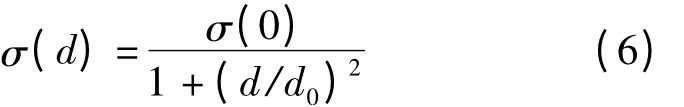
來構造協方差矩陣。

2．最小二乘配置的計算步驟

最小二乘配置的計算步驟如下:

1)選擇趨勢函數;

2)選擇并計算已測點的方差-協方差;

3)計算確定性參數;

4)推估未測點的信號及完全信號估值;

5)精度評定。

3．利用最小二乘配置分析內插點的形變

對于目標的變形監測，一般是通過觀測布設的變形監測參考網網點坐標的變化來分析其形變情況的。如果想了解除網點以外其他點的變形情況，可以用內插或擬合的方法來進行分析，本文利用最小二乘配置對變形監測網的內插點形變情況進行分析。

對目標的形變監測可以分為沉降監測和水平位移監測，本文以沉降監測為例。設沉降監測網共有n個網點，對應的高程分別為hi(i=1，…，n)，有m個內插點。相應的最小二乘配置隨機模型不變，函數模型為

式中，L為觀測值向量;α0、α1、α2為趨勢參數;S為n×1維信號向量;Δ為觀測值誤差向量;未測點信號S'為m維。

通過兩期變形監測的觀測值可以得到兩期觀測值的高程差，然后通過穩定性分析可以得出各網點的實際變形量。將每個網點對應的變形量作為觀測值向量L，利用最小二乘配置可以計算出系數α0、α1、α2，已測點信號S、未測點信號S'和未測點完全信號，也就是m個內插點的沉降估值，未測點信號的權逆陣Σ^S'反映了估值的精度。相關公式推導如下

將式(7)的函數模型用式(1)的形式表示

用AX來表示α0+α1xi+α2yi，Y為隨機參數，包括n維的已測點信號S和g維的未測點信號S'。B=[ I 0]，I為n維單位向量。

對應的誤差方程為

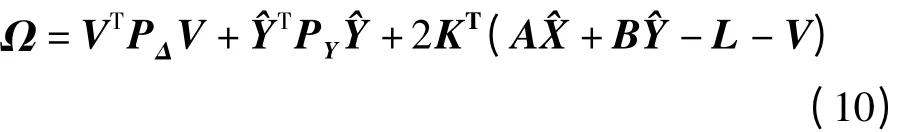
求導，令其等于零

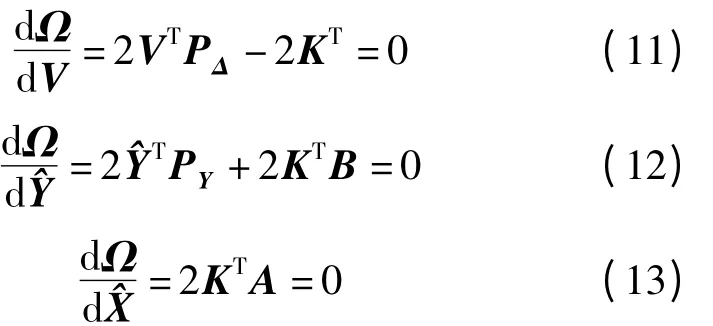
得

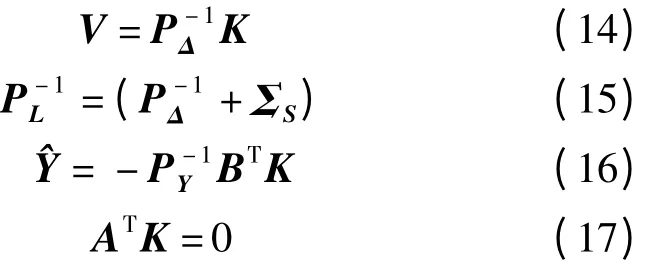
將式(14)、式(16)代入式(9)得

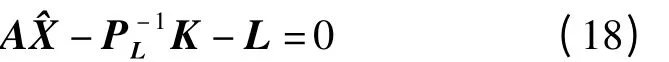
式(18)左乘ATPL，顧及式(17)得

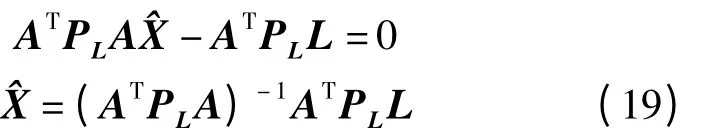
由式(18)得

將式(20)代入式(14)、式(16)得

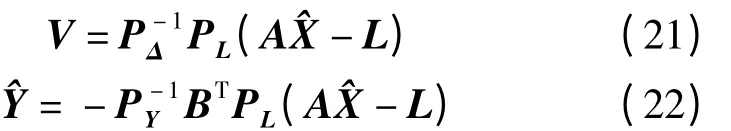
顧及

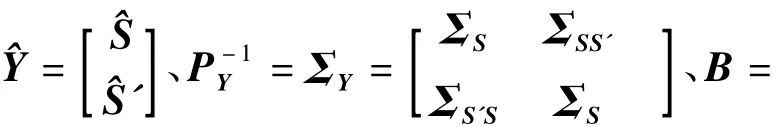
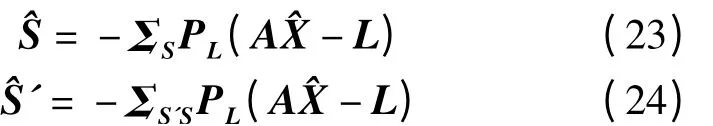
根據誤差傳播定律，可以推導出精度估計式如下

關于信號的權逆陣賦值，選擇經驗函數法，取經驗公式為σ(d)=σ(0)exp(－K2d2)。

三、試驗結果及分析

為了驗證上文所提出的利用最小二乘配置分析變形監測網內插點變形情況的合理性及正確性，下面分別利用一組模擬數據和一組工程數據來進行試驗驗證。

1．模擬試驗

本試驗所使用的數據是模擬數據(如圖1所示)，數據范圍是一個100 m×100 m的矩形變形區域。下面給出試驗中所采用的變形監測網點和檢查點的分布示意圖。

圖1 模擬試驗監測網點和檢查點分布

變形監測網點坐標及兩期模擬沉降值見表1。

模擬變形區域的整體變形趨勢為:任意一點的變形量與它到1號點距離成正比，由此可以得出內插點坐標和理論的沉降值見表2。

取函數模型為

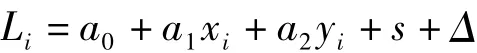
其中，Li為觀測值，α0、α1為趨勢參數，s為信號。隨機模型不變，信號的驗前協方差公式及觀測值的權矩陣公式取σ(d)=0．126exp(－0．36d2)，P=100×I。

計算所得內插點的變形情況見表3。

表1 監測網點坐標和沉降量 m

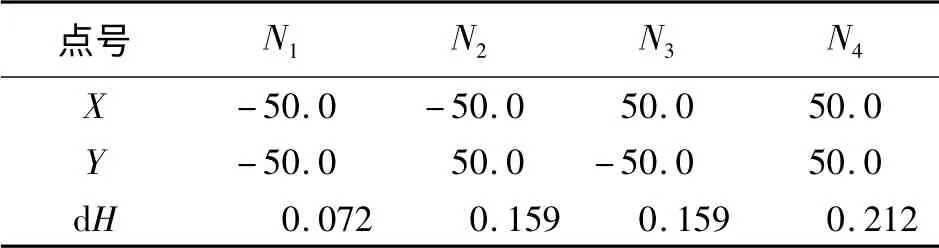
表2 內插點坐標和沉降量 m

表3 預測沉降量與實際沉降量 m

通過比較計算所得的沉降量于所設計的理論值比較可以看出，最小二乘配置計算所得結果精度較高，與理論值相差不超過0．008 m，可以反映出內插點的變形趨勢，因此可以用來分析內插點的變形情況。還可以通過權逆陣來分析計算結果的精度，經過最小二乘配置計算的未測點完全信號的權逆陣如下

2．工程試驗

選擇大連市紅旗街道岔鞍村滑坡監測的工程數據［6］來進行試驗，選擇2010年10月29日和11月21日兩期觀測數據，有點P1—點P10共10個網點，隨機選取P3點和P7點作為內插點，用最小二乘配置原理計算預測其變形情況，然后于實際測量結果進行比較。這里只針對網點和內插點X坐標進行分析。岔鞍村滑坡監測網點坐標及兩期觀測值X方向上形變量見表4。

表4 監測網點坐標和X方向上形變量 m

3號點和7號點的坐標和兩期觀測值X方向上真實形變量見表5。

該試驗中所采用的變形監測網點和檢查點的分布示意如圖2所示。

函數模型和信號的驗前協方差公式及觀測值的權矩陣公式與模擬試驗一致，計算內插點的變形情況見表6。

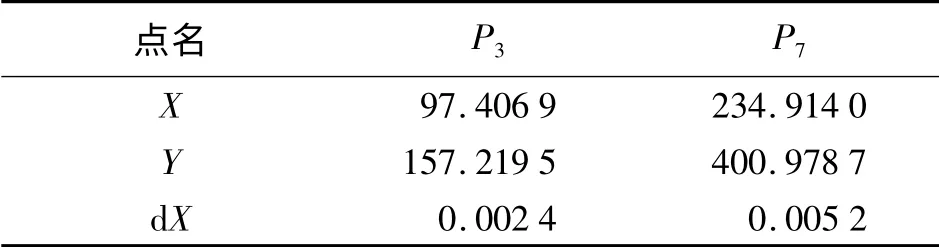
表5 內插點坐標和X 方向上真實形變量 m

圖2 真實試驗監測網點和檢查點分布

表6 X方向實際形變量與預測形變量 m

通過比較計算所得的沉降量與點位的實際觀測形變量比較可以看出，在工程試驗中，計算值與實際形變量相差較大，但可以反映出內插點的變形趨勢，因此可以用來分析內插點的變形情況。還可以通過權逆陣來分析計算結果的精度，經過最小二乘配置計算的未測點完全信號的權逆陣如下

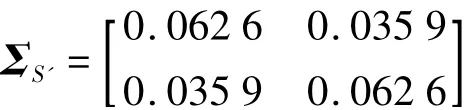
由試驗結果數據可以看出，采用模擬數據進行試驗所得到的結果精度很高，證明本文利用最小二乘配置原理來分析變形監測控制網內插點變形情況是可行的;采用真實數據進行試驗所得到的結果與實際測量結果相差較大，其原因是有些網點的變形具有特殊性，但仍然可以反映出內插點的變形趨勢，并可以通過未測點完全信號的協方差陣來評價預測形變量的精度，因此該方法可以用來分析內插點的變形情況。兩組試驗結果表明，本文提出的基于最小二乘配置原理的變形監測網內插點形變分析的方法是可行的。

四、結束語

本文從最小二乘配置理論出發，推導了預測變形監測網內插點形變量的計算公式和精度估計式，并通過模擬數據試驗和工程數據試驗，驗證了該方法的正確性和有效性，得出了最小二乘配置可以用于分析變形監測網內插點變形分析的結論。相比較于直接內插或擬合的方法求內插點的變形量，最小二乘配置的優勢在于可以在提供預測值的同時進行精度評定，對于精度較低的預測結果可以舍棄，以保證對預測點形變信息預測分析的可靠性。

［1］ 張希，江在森，用最小二乘配置獲得地形變應變場動態圖像的幾個問題研究［J］．地殼形變與地震，1999(3):32-39．

［2］ 杜紅飛，謝劭峰，孫昌瑜．最小二乘配置法在GPS高程異常值推估中的應用［J］．河南科學，2013(2):208-211．

［3］ 黃維彬．近代平差理論及其應用［M］．北京:解放軍出版社，1990．

［4］ 柴洪洲．地殼運動背景場及其監測網數據處理理論與方法研究［D］．鄭州:解放軍信息工程大學，2006．

［5］ 柴洪洲，崔岳，明鋒．最小二乘配置方法確定中國大陸主要塊體運動模型［J］．測繪學報，2009，38(1):61-65．

［6］ 朱爽．大連市紅旗街道岔鞍村滑坡監測研究［D］．長春:吉林大學，2014．