11 輥矯直機矯直過程中性層偏移量分析
李長樂,桂海蓮,李 曜
(太原科技大學材料學院,山西 太原 030024;太原科技大學機械學院,山西 太原 030024)
0 前言
《2011~2020 年中國鋼鐵工業科學與技術發展指南》[1]中將“新一代可循環鋼鐵流程工藝與裝備技術”和“新一代控軋控冷技術”作為鋼鐵行業“十二五”期間重點優化、完善和推廣的關鍵技術,對鋼板的工藝流程和裝備技術提出更高要求。《指南》指出“關于智能化鋼鐵生產的各項技術研發、推廣優化的問題已十分迫切地擺在我們面前。這是現代化鋼廠實施以計算機全自動、高精度控制鋼鐵生產全過程工藝與裝備,實現生產效率最高、物耗能耗最低、生產成本最小、產品質量最佳、排放趨零總體目標的必要條件。”做為提高鋼板產品質量的矯直設備,更應該從基礎理論對矯直過程進行研究,建立合理的矯直力模型,以適應生產的需要,為高精度、高效率生產提供必要的技術支持。
輥式矯直機矯直過程的研究一般采用解析法或數值分析法,并且近年來數值分析方法應用更加廣泛。崔甫[2]是我國較早研究矯直理論與計算的學者,他曾系統的分析了影響矯直力的眾多參數。楊曉君[3]利用Marc 對十一輥矯直過程進行有限元模擬并分析了截面上各種應力應變的分布規律。周曉宇[4]確定了中厚板輥矯中壓彎量、彎輥凸度等參數,并利用VB 語言編寫中厚板冷矯直工藝計算軟件。張衛紅[5]在傳統力能參數模型的基礎上,對11 輥板帶矯直機進行分析研究,提出了一種基于虛擬支點和曲線擬合的新力能參數計算模型。東北大學薛軍安[6]研究了輥式矯直過程中接觸傾角與曲率的變化規律,說明接觸傾角具有累計效應。武漢科技大學楊云[7]研究了七輥矯直機矯直力計算模型,太原科技大學周存龍[8,9]利用面積-力矩第二定律,建立了彎矩與撓度的關系式,確定了輥式矯直過程中板帶的彎曲撓度。太原科技大學王效崗[10,11]對十五輥組合矯直機的關鍵技術進行了系統研究。本文重點研究中性層偏移在矯直過程中的作用,確定中性層偏移計算公式,結合數值分析擬合中性層偏移變化曲線,為矯直力模型的精確確定提供理論依據。
1 理論分析中性層偏移量
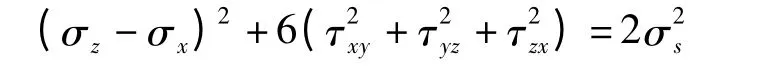
對于平面應變問題可簡化為
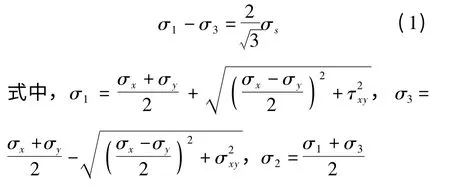
在傳統矯直理論中,認為矯直件在矯直過程中幾何中心層與應力中性層是重合的,如圖1a所示,在整個矯直過程中應力中性層不會發生偏移。在某些特定的情況下,中性層偏移量相對于矯直件厚度是不可忽略的,它的偏移形式如圖1b 所示。在圖1a 中,應力中性層處于板厚中心位置,上下拉伸區和壓縮區的彈性變形區相等,上下表面的應力值σx=σx';但在圖1b 中,由于應力中性層向下發生了偏移,所以以幾何中心層為界產生的彈性區厚度不同,并且上下表面的應力值也不同。
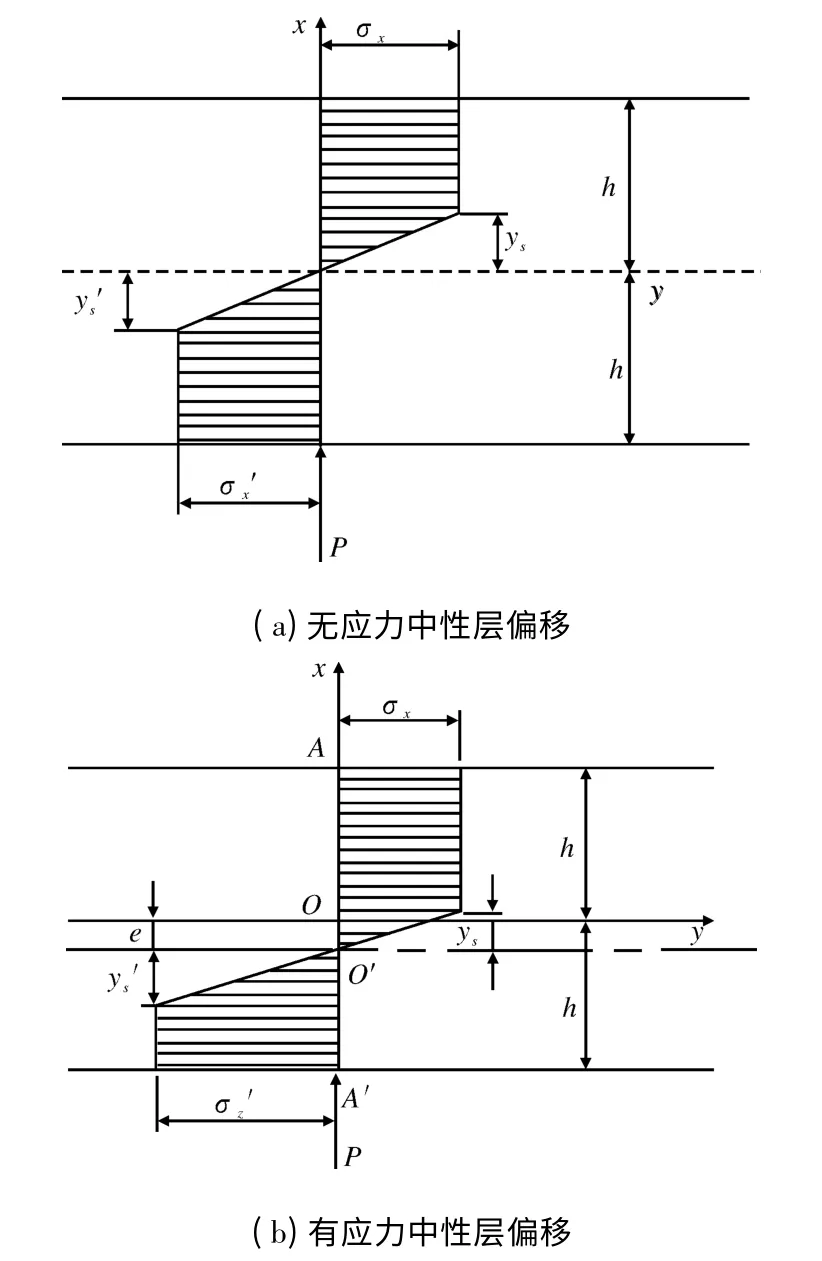
圖1 理想材料彈塑性彎曲應力圖Fig.1 Plastic bending of perfect material
假設中性層向下發生偏移,偏移量為e,如果e >0,則說明應力中性層向下發生了偏移;如何e <0,則說明應力中性層向上發生了偏移;如何e=0,則說明應力中性層沒有發生偏移。根據上述分析,由∑Px=0 得
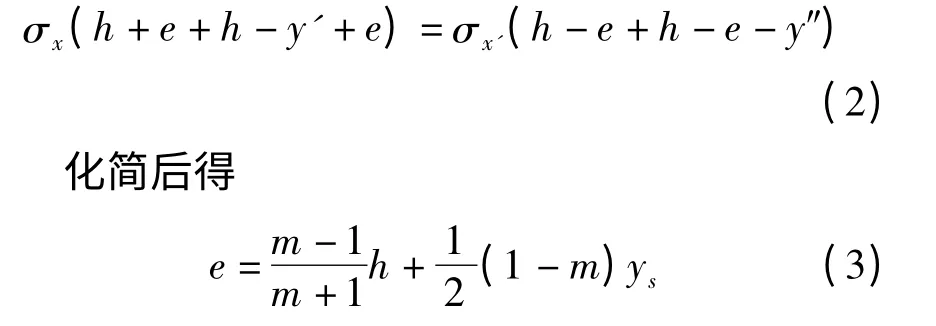
不考慮中性層偏移的力矩公式[12]為
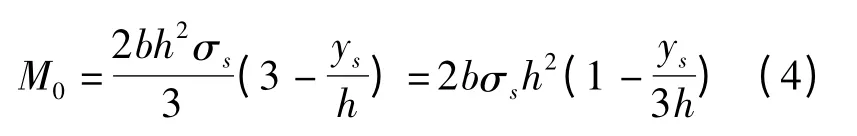
考慮中性層偏移的力矩公式為:
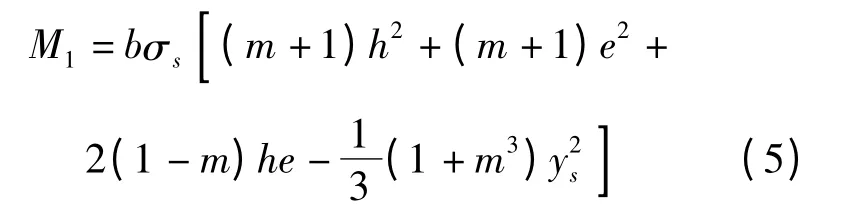
2 數值分析計算
計算模型來源于本實驗室的11 輥全液壓矯直機實驗平臺,如圖2 所示。在ansys 有限元分析軟件中建立模型,如圖3 所示。模型為軋輥半徑0.06 m,板尺寸為:1.2 m ×0.08 m ×0.6 m(長×厚×寬),板的相對原始曲率為5.18。

圖2 全液壓矯直機實驗平臺Fig.2 11 rollers plate leveler

圖3 計算模型Fig.3 The calculation model
取一個矯直單元,如圖4 所示。對施加不同力后矯直件橫截面的彈塑性變形進行研究分析,觀察幾何中心層上下拉伸區和壓縮區的塑性變形規律,進而研究中心層偏移的變化。
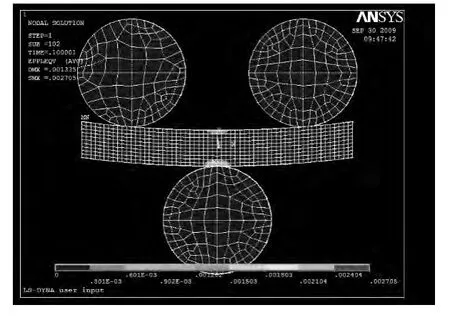
圖4 一個矯直單元Fig.4 A straightening unit
2.1 受力2 MN
從圖5 中可知拉伸區和壓縮區均發生了塑性變形,但二者的變形程度有所不同。經過測量得知:中性軸左側上半部分的彈性區為31.5 mm,下半部分的彈性區為26.9 mm,所以中性層向上偏移約為2.3 mm,中性軸上半部分的彈性區為30.3 mm,下半部分的彈性區為30.1 mm,所以中性層向上偏移約為0.1 mm,中心軸右側上半部分的彈性區為31.3 mm,下半部分的彈性區為27.2 mm,所以中性層向上偏移約為2.05 mm。這說明塑性變形最大的區域不再中性軸處,而是在其左右兩側。從測量數據可以看出中性層偏移最大的是發生在中性軸兩側,并非是中性軸上。
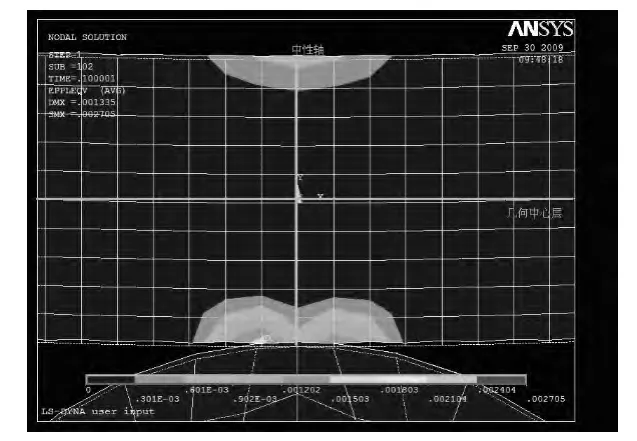
圖5 局部細化圖Fig.5 Local thinning image
利用公式(3)、(4)和(5)計算得到的中性層偏移量和彎矩的值為:
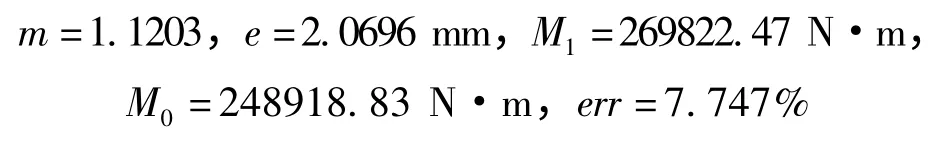
2.2 受力2.5 MN
圖6 和圖4 比較可知,隨著受力的增大,塑性區也在不斷增大。從圖7 中測量得到中性軸左側上半部分的彈性區為24.2 mm,下半部分的彈性區為24 mm,所以中性層向上偏移約為0.1 mm,中性軸上半部分的彈性區為24.1 mm,下半部分的彈性區為26.3 mm,所以中性層向下偏移約為1.1 mm,中心軸右側上半部分的彈性區為24.2 mm,下半部分的彈性區為24 mm,所以中性層向上偏移約為0.1 mm。
利用上一部分推導的中性層偏移量計算公式得到的中性層偏移量的值為:
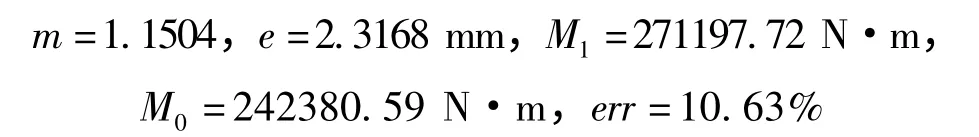
利用上述計算結果,對中性層偏移量進行數據擬合,擬合曲線如圖8 所示。
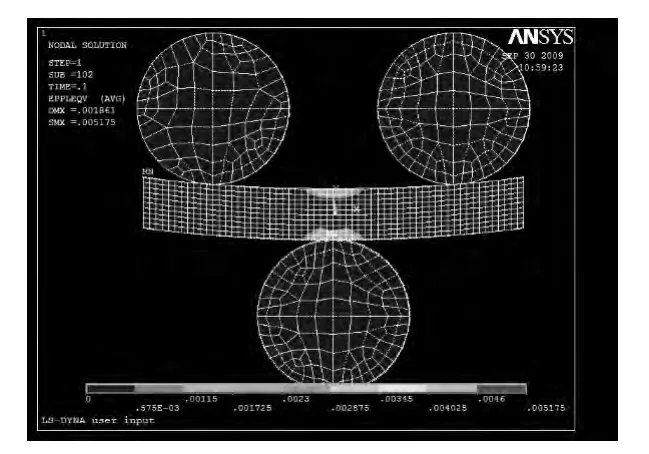
圖6 一個矯直單元Fig.6 A straightening unit
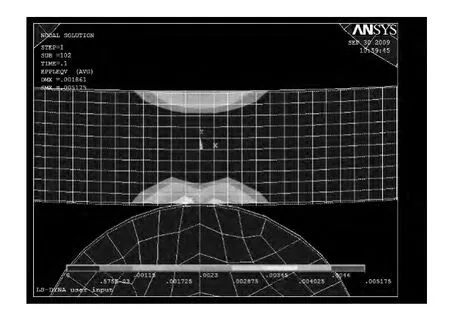
圖7 局部細化圖Fig.7 Local thinning image
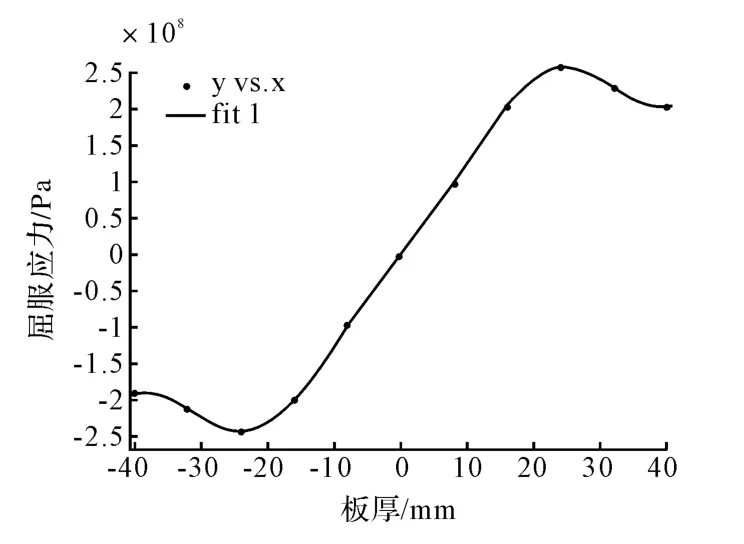
圖8 數據擬合曲線Fig.8 Fitting curve
3 結論
本文首先通過力學推導,得到中性層偏移的計算公式,并推導出考慮中性層偏移時的彎矩力矩計算公式。通過有限元分析和測量,說明在中厚板輥式矯直過程中,中性層偏移是存在的,并且將測量值與理論計算值進行了對比,是否考慮中性層偏移導致的力矩的誤差在10%左右。這說明中性層偏移量對矯直力的精確確定具有一定的影響,所以在矯直力模型的建立中應當考慮中性層偏移這個影響因素。
[1]中國金屬學會,中國鋼鐵工業協會編.2011~2020年中國鋼鐵工業科學與技術發展指南[C].北京:冶金工業出版社,2012.
[2]崔甫.矯直原理與矯直機械(第2 版)[M].北京:冶金工業出版社,2007
[3]楊曉君.中厚板輥式矯直過程算法模型修正[D].太原:太原科技大學,2011.
[4]周曉宇.中厚板冷矯直工藝參數研究及數學模型優化[D].太原:太原科技大學,2011.
[5]張紅衛.基于虛擬支點與曲線擬合的板帶矯直機力能參數模型研究[D].武漢:武漢科技大學,2011.
[6]薛軍安,崔麗,胡賢磊,等.輥式矯直過程的接觸傾角與曲率耦合分析[J].中國冶金,2009,19(2):23-26.
[7]楊云,李友榮,王志剛.七輥板帶矯直機矯直力計算模型研究[J].冶金設備,2009(2):55-57.
[8]周存龍,王國棟,謝東鋼,等.輥式矯直過程中板帶彎曲撓度的確定[J].太原科技大學學報,2009,30(1):48-50.
[9]周存龍,王國棟,劉相華.壓彎量對軋件矯直變形影響的有限元分析[J].塑性工程學報,2006,13(1):78-81.
[10]王效崗,黃慶學,馬勤.中厚板的橫向波浪矯直研究[J].中國機械工程,2009,20(1):95-98.
[11]王效崗.十五輥組合矯直機關鍵技術及理論模型的研究[D].蘭州:蘭州理工大學,2008.
[12]黃慶學.軋鋼機械設計[M].北京:冶金工業出版社,2007.
[13]Hai-Lian Gui,Qiang Li,Qing-Xue Huang.Analysis of rolled piece deformation in straightening process using FM-BEM[J].Journal of marine science and technology,2014,22(5):550-556.

