自由配光設計中的復合拋物面三維同步多表面方法

梁 雪,王 賽,龐宇峰

(杭州照相機械研究所, 浙江 杭州 310023)

?

自由配光設計中的復合拋物面三維同步多表面方法

梁 雪,王 賽,龐宇峰

(杭州照相機械研究所, 浙江 杭州 310023)

為實現LED朗伯光源的矩形配光，提出了一種基于“脊肋”法的三維同步多表面非成像光學設計方法。該方法根據給定的輻照度分布，先由復合拋物面(CPC)完成初級配光，將朗伯光源±90°的發散角縮小到45°，再在二維平面生成一對“脊”線，然后向兩側生長出“肋”線，生成兩個曲面框架，最后利用由NURBS曲面算法構建出兩個自由曲面實現目標配光。兩個自由曲面的引入提升了設計的自由度，但也大大增加了設計難度。將該方法應用到矩形均勻配光設計中，仿真結果表明：在遠場接收面上得到一個較規則的方形輪廓且光束半發散角約為3.66°，考慮反射損失后其光效仍高達63%以上，平頂均勻度高于0.96。

幾何光學；非成像光學；三維同步多表面

引言

LED具有體積小、壽命長、光效高等特點，已廣泛應用于商業照明、汽車照明、景觀照明等領域[1]。

由于LED是一種朗伯型光源，非各向同性光源，因此有必要研發針對擴展光源的非成像光學設計方法。目前主要有截邊法、微分方程法、同步多表面設計法(SMS，Simultaneous Multiple Surface)等，其中SMS已成為針對擴展光源非成像光學設計的重要方法。SMS設計方法考慮LED端點處發出的邊緣光線進行多個表面的同步設計[2,3]。SMS方法可分為二維和三維兩種情況，二維設計方法適用于軸對稱配光的光學器件設計，而三維設計適用于非軸對稱配光的光學鏡頭設計，其光學表面通常為自由曲面。

本文是對二維SMS設計方法[5]的進一步深化和拓展，針對LED朗伯光源的矩形配光，提出一種三維同步多表面非成像光學設計方法。該方法根據給定輻照度分布，首先利用復合拋物面集光器縮小LED光源發散角，再在二維平面生成一對“脊”線并向兩側生長出“肋”線，最后利用NURBS算法構建自由光學曲面，實現矩形配光的非成像光學設計。本文方法對提高LED配光水平和應用推廣具有重要意義。

1 設計方法

同步多表面設計方法(SMS)來源于其允許對多個光學表面同時進行設計的性質[2-4]。應用SMS設計方法可以設計出如下幾種光學器件：(1)折射/折射(RR)器件；(2)折射/反射(RX)器件；(3)反射/折射(XR)器件；(4)折射/反射/全反射(RXI)器件[5]。一般情況上述器件都是在二維平面內進行同步輪廓設計，通過繞軸旋轉得到光學器件模型，相比之下三維情況的設計則十分復雜。

三維空間的SMS設計以二維設計為基礎，光源尺寸已知，首先選定兩個輪廓曲線的起始點及其對應的法線方向，在保證光學擴展量守恒的前提下，由起點開始順序的應用折射或反射定律以確定光線的入射點和該點處的法線方向。根據這一機理，可以在計算機程序的輔助下得到二維平面上的一系列的參數點，這些參數點在空間中便鏈接成了兩條“脊”點鏈。再根據這兩條點鏈數據向空間中伸出多條“肋”，最終得到一個類似于動物胸腔骨架的結構，根據骨架上各點的坐標數據可以通過NURBS曲面建模生成上下兩個光學表面。由于每一根“肋”的生成都由最初在二維情況下得到的“脊”決定，因此將該三維設計方法形象的稱為SMS器件的“脊肋”法。

2 三維同步多表面設計

未進行任何初級配光的LED光源可看作是一個朗伯發光體，其光強分布遵循式(1)。

(1)

其中θ為光線與光源法線的夾角,θ∈(0,π/2)。三維情況下，平面光源某面元dA其光學擴展量dU可以表示為

(2)

n為反射器內部介質折射率，dΩ為包含光線的立體角元，dφ為立體角元在光源面上投影的偏向角[2,5]。對dU積分可得整個光源面的光學擴展量

(3)

AI為光源面的尺寸。根據光學擴展量守恒，理想非成像光學器件出口處光學擴展量也為U，且U=0.5πn2AOcosβ，β為出射光線與法線夾角，AO為光學器件出射面面積。由式(3)可知，當系統光學擴展量確定后，出射光線的發散角越小，出射面尺寸越大。對于LED光源，必須令XX器件的出射面積足夠大以提供較小的光線發散角。XX器件的尺寸包含有效區域和結構區域兩部分，利用折射/全反射/反射/折射(即RIXR)的結構，可以最大限度的收集光源的光線，縮小結構區域，從而減小整個光學器件尺寸[5]。

2.1 初級配光：CPC設計

復合拋物面集光器(CPC)最初設計用來匯聚由無限遠處光源發出的包含在某一立體角內的光線[2]。根據光路可逆原理，可以將CPC逆向使用作為LED的配光器件[5,6]，其主要作用是縮小LED光線的發散角。本文以方形LED為光源，不具備軸對稱性質，因此考慮設計一種新型非軸對稱的CPC配光器件，其光線入口和出口均為方形。

在圖1中，xy平面內的方形區域為LED光源。為不失一般性且簡化計算，令光源方形出光面的尺寸為2a(a≠0)，則該光源在x軸方向上兩側端點分別設定為F1(-a,0,0)和F2(a,0,0)。可首先在xz平面內建立二維CPC，由F1發出的邊緣光線在二維CPC出口處反射后仍為邊緣光線，其與水平方向的夾角為α。CPC側壁具有這樣的性質：由光源端點發出的全部邊緣光線經側壁反射后均變為與水平方向夾角為α的平行光線。在xz平面內，給定焦點F1，對稱軸偏離水平方向角度為α且經過F2點的拋物線可由式(4)給出。

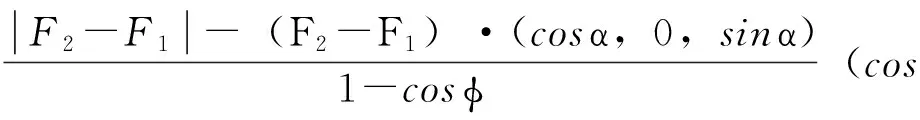
(4)其中φ為F1發出的某光線與拋物線對稱軸(圖1中過F1的虛線)之間的夾角。由式(4)建立的拋物線經過鏡像和截取，可以得到一個二維情況下的CPC輪廓(圖1中E1E2F2F1)。同理在y-z平面內建立相同的CPC輪廓，并將所得的兩個CPC輪廓分別沿x、y軸拉伸，將得到如圖1所示的CPC結構，該CPC的入口和出口均為方形。由于出口處的面積變大，則根據光學擴展量守恒，出口處的出射光線立體角將變小。若考慮α=145°，光學仿真結果表明該CPC初級配光后的配光曲線如圖2所示，三條曲線分別為0°、45°和90°方向上的坎德拉分布。通過方形出口CPC器件初級配光，將光源光線的發散角控制在±45°之間，從而控制XX反射器件的尺寸。

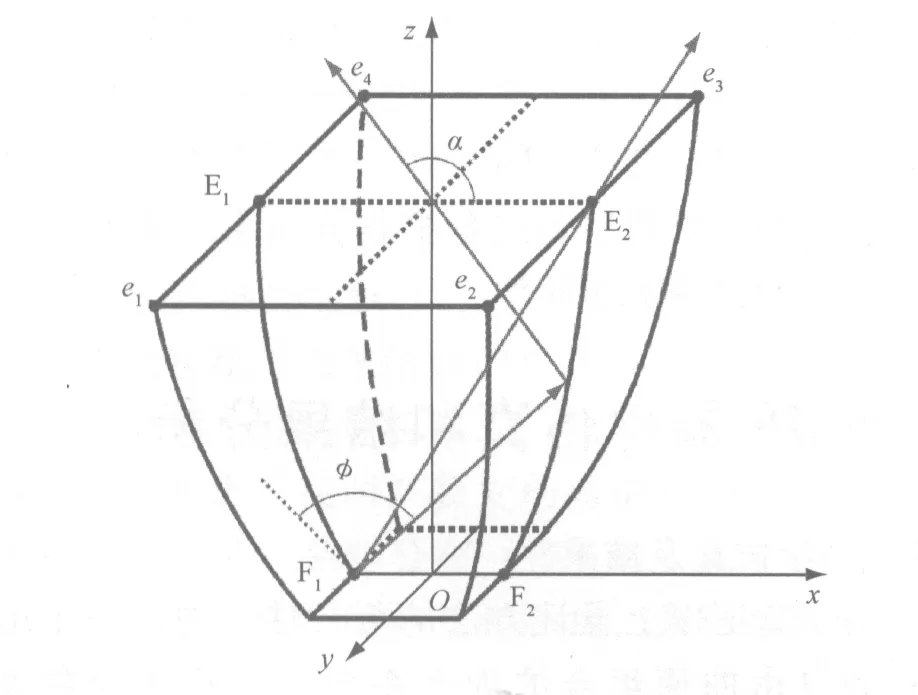
圖1 CPC反射器結構示意圖Fig.1 The structure of the CPC

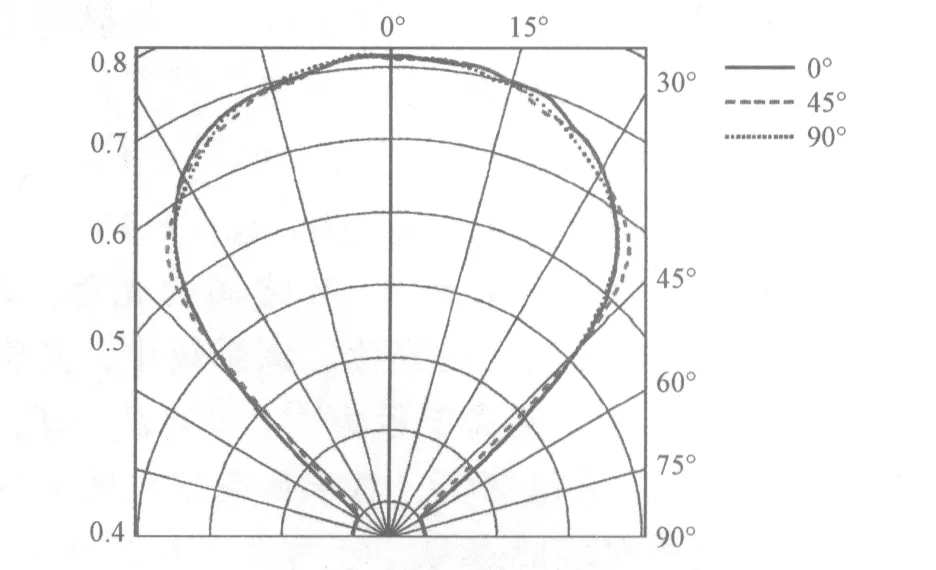
圖2 經CPC配光后LED的配光曲線Fig.2 The intensity distribution curve after reflected by the CPC

2.2 次級配光：SMS“脊肋”設計[2, 5-11]

初級配光后，LED發出的光線其發散角由±90°縮小到±45°，發光面也由方形LED表面變為CPC出口處的方形“虛光源”，因此在SMS設計中將以該虛光源端點為基礎進行同步表面設計。如圖3所示,e1、e2、e3和e4分別為該區域的邊緣點。

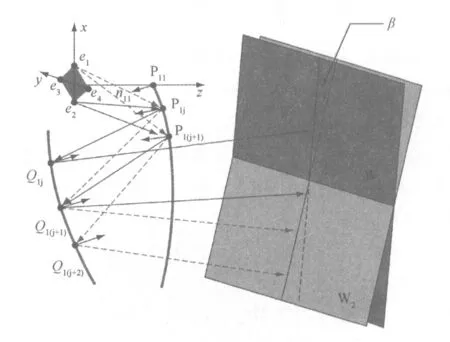
圖3 “脊椎點鏈”的生成Fig.3 Generation of the vertebrae chain

2.2.1 “脊”的生成

在SMS的三維設計中“脊”點鏈的生成是尤為重要的，因為該點鏈決定了向空間中伸出的每一條“肋”的起始點及該點處的法線方向。

“脊”點鏈的生成與二維情況的SMS器件設計相同，需要首先確定如下幾個量：(1)上反射表面的起始點位置；(2)平面波前法向及其夾角β；(3)起始點處反射表面的法矢量n；(4)光源各端點光線在經過多表面的反射后到達其對應波前所傳播的光程[5, 7]。如圖3所示，w2、w1分別為光源端點e1和e2發出的邊緣光線經多表面反射器反射后的對應波前，兩波前之間夾角β同時也是出射邊緣光線的發散角。P1j是上表面“脊”點鏈上的一點，當j=1時P1j即為“脊”點鏈的起始點。由于n11和波前方向已知，故光線e2P11關于法線n11的反射光線方向也可以確定，該反射光線同時又是下表面點鏈Q11點處的入射光線，因此可以根據式(4)中設定的光程以及反射定律確定出Q11點的位置和該點處的法線方向。同理，根據光源端點e1發出的邊緣光線e1P11和e1→w2的光程，Q12的位置也能夠確定。由光學擴展量守恒可得對于光源端點發出并射向上表面點鏈起始點P11的兩條邊緣光線有[2-5, 10]：

(5)

式(5)中[A,B]表示點A、B之間的光程，Γ為邊緣光線到達對應波前的光程。該系統中，光學擴展量可以用光程差形式表示為[2]：U=Γ2-Γ1。為保證系統光學擴展量守恒，對于待確定點鏈上的任意點P1j和它所對應的點Q1j(j為大于0的整數)應滿足如下關系：

(6)

根據式(6)可同步計算出上下兩條點鏈，即用于生成“肋”的“脊”點鏈。

2.2.2 “肋”的生成

在2.2.1中已經得到了構成同步多表面的兩條“脊”點鏈，該點鏈由位于同一二維平面內的一系列點連接而成。“脊”生成的同時也得到了每一點處的法線方向，因此在圖3中的上表面點鏈，任一點P1j都對應一個初始法線方向n1j。由于設計空間增加了一個維度，需要引入一組新的波前w3、w4，波前w3與w4夾角為γ(為簡化起見令γ=β)，如圖4所示。“脊”的生成主要根據光源端點e1、e2發出的邊緣光線完成，而“肋”生成中將主要利用位于另一方向上的光源端點e3、e4。

圖4 “肋骨”的生成Fig.4 Generation of the rib chains

由于上表面起始點P11以及該點處的法向量n11已經確定，因此“肋線”的生成仍以該點為起始并根據n11開始設計。圖4中，光源端點E4對應波前w4，因此e4點射向P11點的光線將在Q11點反射并最終射向w4；端點e3發出的邊緣光線經P11點偏折后射向下表面并最終入射到其對應波前w3。指定e4、e3到其對應波前w4、w3的光程為Γ4、Γ3，則可以通過下式得到反射點Q21的位置：

(7)

再次根據光學擴展量守恒并參照式(6)便可得到向xy平面一側伸出的一組“肋”點鏈。對于空間中的任意條“肋”點鏈，都有：

U={[E3,Pij]+[Pij,Q(i+1)j]+[Q(i+1)j,w3]}-{[E2,Pij]+[Pij,Qij]+[Qij,w4]}

(8)

式中Pij和Qij分別為上、下表面第j條“肋”點鏈上的第i個光線入射點。當i、j取不同數值時便可由式(8)得到1/4空間內的SMS“脊肋”數據點，通過關于xy平面和yz平面內的兩次鏡像將得到整個空間中的SMS數據，將這些數據通過NURBS曲面建模，最終得到上下兩個NURBS曲面。由于前文中已經設計了一種方形出口的CPC器件將LED光源發出的光線控制在±45°范圍內，因此需要對SMS的上表面進行裁剪除去多余的自由曲面，盡量降低反射面對光線的遮擋。同時對SMS下表面進行處理以安置光源，處理后通過建模軟件對上下表面實體化生成光學器件實體模型。

3 SMS器件仿真和結果分析

3.1 光學仿真及結果

為了驗證以上設計方法的可行性，構建一個由CPC和自由曲面組合的配光系統，其具體參數如下：在方口CPC的入口處設定表面光源屬性為朗伯發光體且發射功率為10W，追跡光線為200萬條。CPC及SMS表面設置為反射率約為0.94，在近場(0.1m)和遠場(1m、5m、10m)處分別插入接收面，用于檢測器件的輻照分布情況。圖5位于3個位置處接收面上的照度分布情況。

圖5中，a、b、c、d分別為距離光源0.1m、1m、5m和10m處接收面上入射光線的照度分布。通過對比可知在近場(0.1m)處3D-SMS器件形成的照度分布效果一般，為一不均勻亮環；遠場情況下，照度圖的中心處開始出現明顯的方形區域(圖5(b)所示)；隨著距離的進一步增加，該方形區域逐漸增大，整個輻照度分布也由近場時的亮環變為方形均勻分布。由圖5中c、d可粗略估計，3D-SMS器件在遠場處形成的光斑其邊長分別約為1m和2m。同時，光學仿真結果還表明，考慮介質吸收和反射損耗的情況下，檢測平面接收到的光效約為0.63。

圖5 不同距離處接受面上照度分布情況Fig.5 Irradiance distribution on different target planes

3.2 照度分布特性及系統光效分析

由SMS器件的設計過程可知，某一截面上光源發出的光線經過光學結構的反射被分為左右兩部分出射。由于光束發散角較小，在距離光源較近的區域光強主要集中在兩個獨立的峰值曲線上，因此近場時照度將呈一亮環分布(圖5a)。隨著距離的增大，這些峰逐漸擴展并互相疊加，最終呈現輻射照度在檢測平面上的均勻分布[5]。

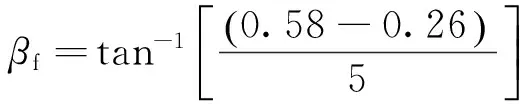
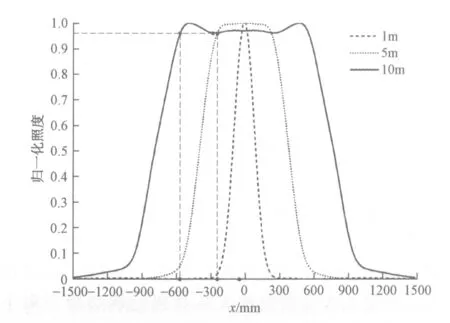
圖6 檢測平面照度歸一化剖面曲線Fig.6 The normalized profile curve of irradiance on target plane

3.3 透鏡加工及實際效果分析

經過本設計方法設計得到的透鏡實體如圖7所示。

圖7 透鏡實體模型Fig.7 Model of the lens

為了確認本設計方法的可行性，對透鏡進行了樣品的加工，根據現有的COB光源發光面尺寸對透鏡的相關尺寸進行了等比例的調整，考慮到成本問題，并未開模僅使用五軸加工機加工了手板樣品。

圖8 透鏡樣品照明效果實測結果Fig.8 Result of the luminous effect of the lens

圖8為該透鏡樣品的實際照明效果，由于對透鏡進行了等比例的縮小，因此照明距離也相應的縮短，圖8中為1m處的照明效果，由圖8可見，該透鏡可以將COB光源發出的光線在1m處實現輻照度的方形分布，且均勻度良好。

4 結論

本文提出了一種基于“脊肋”法的三維同步多表面設計方法并構建模型進行了仿真驗證，得到良好效果。仿真結果表明，應用該方法構建的三維SMS器件能夠在遠場處產生規則的方形輻照度分布，考慮損耗時遠場接收面上的光效大于0.63；平頂寬度范圍內的方輻照度均勻度大于0.96；根據該區域尺寸隨光線傳播的擴大計算出遠場邊緣光束半發散角約為3.66°，準直性良好，能夠滿足準直和投影等應用的要求，對非成像光學相關產業的發展具有重要意義。

[1] 周志敏，紀愛華. 大功率LED照明技術設計與應用[M]. 北京：電子工業出版社, 2011:1-10.

[2] JULIO C. Introduction to nonimaging optics [M]. New York: CRC Press.2008:55-116,271-324,471-474.

[3] Harald R, Ari R. Edge-ray principle of nonimaging optics[J]. Opt. Soc. Am. A., 1994,11(10):2627-2632.

[4] Roland Winston, Juan C Miano, Pablo Benítez. Nonimaging Optics [M]. London: Elsevier Academic Press. 2005:184-221.

[5] 張航,梁雪,嚴金華,等. LED準直器設計中復合拋物面同步多曲面方法[J]. 光學學報, 2012, 32(9): 0922004.

[6] Roland Winston，Jeffrey M. Gordon. Planar Concentrators Near The Etendue Limit [J]. Opt. Let, 2005, 30(9):2617-2619.

[7] Benítez P, Miano J C, Blen J, et al. Simultaneous Multiple Surface Optical Design Method in Three Dimensions [J]. Opt. Eng, 2004, 43(7): 1489-1502.

[8] Oliver Dross, Rubén Mohedano, Pablo Benítez, et al. Review of SMS Design Methods and Real World Applications [J]. SPIE. 2004:35-47.

[10] Fernando Munoz, Pablo Benitez, et al. Simultaneous Multiple Surface Design of Compact Air-Gap Collimators for Light-Emitting Diodes[J]. Opt. Eng, 2004,43(7):1522-1530.

[11] 羅滔，錢可元，羅毅. 面向投影儀的LED陣列單位Etendue光通量的研究[J]. 半導體光電,2008,29(1):41-45.

《照明工程學報》首次申請國際期刊刊名代碼(CODEN)已獲批準

近日，《照明工程學報》編輯部與國際CODEN服務部(International CODEN Service)聯系，申請國際期刊刊名代碼CODEN碼。經國際CODEN中心查核、確認，通知《照明工程學報》被分配、加工的CODEN碼為ZGXHBE。本刊將從2015年26卷第2期開始，將CODEN碼印刷在期刊封面右上角國際標準刊號ISSN 1004-440X和國內統一刊號CN11-3029/TM下方。

CODEN (Code Number)是國際公認代碼，《工程索引》(EI各種版本)、《烏利希期刊指南》(Ulrich's PD)、科學引文索引(SCI)、《斯高帕斯數據庫》(Scopus)、《科學文摘》(SA, INSPEC)等國際數據庫均采用CODEN碼進行文獻/期刊識別。《照明工程學報》CODEN代碼的獲得使期刊在國內外檢索和引用中又增加了一個重要標識，將大大促進本刊在國內外的交流，推進期刊的國際化進程。

Compound Parabolic Concentrator-Simultaneously Multiple Surface Method for Rectangualar Optical Design in 3D Space

Liang Xue, Wang Sai, Pang Yufeng

(HangzhouPhotographicMachineryResearchInstitute,Hangzhou310023,China)

In order to achieve the rectangular irradiance distribution of LED lambertian source, a simultaneously multiple surface nonimaging optical design method is put forward which is called the “spine-rib” method. First it shrinks the divergence of the lambertian source from ±90° to 45° by a CPC, and then a couple of “spine” line is generated according to the prescribed irradiance distribution. Based on these lines there will be “rib” lines grown on to both side to get two surface frameworks. Finally, two freeform surfaces of the optical device are built by NURBS surface algorithm. The introduction of two freeform surfaces enhances the degrees of freedom which also improves the difficulty of design. Applied the method to the rectangular uniform light distribution design, simulation results show that: a square contour will be formed on the far-field receiver and give a 3.66° ray half divergence angle. When the reflection loss is fully considered, the light energy utilization is still more than 63%, the flat-topped uniformity is higher than 0.96.

geometric optics; nonimaging optics;3D-SMS methods

杭州市科研院所技術研發研究專項

O345

A

10.3969/j.issn.1004-440X.2015.02.018