基于模糊識別的地下水評價

張鐘元

(黑龍江省水利水電勘測設計研究院，哈爾濱150080)

0 引言

了解中國的地下水水質狀況，根據地下水水質現狀評價成果，密切結合污染源種類、物質組成和地理分布特征，通過綜合分析，確定污染范圍，并探討地下水污染的成因。至今為止，國內外學者做了大量的研究，依據《地下水質量標準》(GB/T1448－93)，提出了很多的地下水水質評價的方法，比如BP神經網絡模型、灰色關聯聚類、熵權的模糊物元、模糊綜合評判法、相關性分析方法、模糊數學法［1］等，并取得了一定的研究成果。文章結合石家莊地區2004年地下水水質統測數據的實例，應用工程模糊集理論中的二元比較方法確定權重以及模糊識別模型來進行地下水水質評價，取得較為良好的效果，模糊識別模型較其它方法相對簡便，結果也較為理想。為制定地下水資源可持續開發利用政策、措施提供技術依據。

1 二元比較

設基本單元系統中有因素集公式為:

其重要性的二元對比矩陣為:

若滿足條件:

1)當fhk＞fhl時，有fkl=0

2)當fhk＜fhl時，有fkl=1

3)當fhk=fhl時，有fkl=0.5

則矩陣F必須滿足重要性定性排序的傳遞性，F稱為重要性排序一致性標度矩陣，h=1，2，…，n。

2 模糊識別模型［2］

設有需要對模糊概念或模糊子集A進行識別的n個樣本組成的組合，有m個指標(或目標)特征值表示樣本的整體特征，則有樣本集的指標(或目標)特征值矩陣:

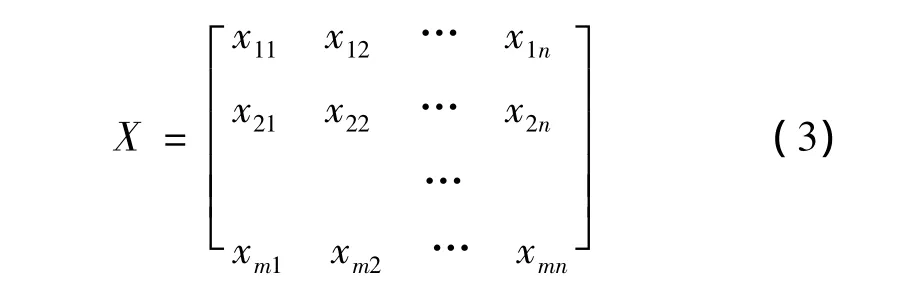
式中:xij為樣本j指標i的特征值，i=1，2，…，m;j= 1，2，...，n。

如樣本集依據m個指標按c個狀態或級別的已知指標標準特征值進行識別，則有指標標準特征值矩陣:

式中:yih為狀態或級別h指標i標準特征值，h=1，2，…，c;i=1，2，…，m。

當指標從1級變至c級指標標準特征值增加時，指標對A的相對隸屬度(隸屬函數)為:

h級指標標準特征值對A的相對隸屬度(隸屬函數)為:

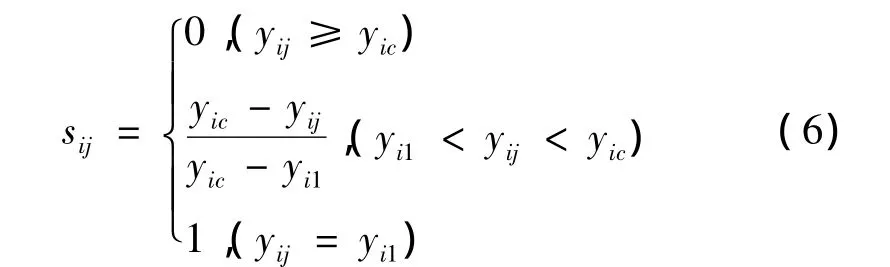
此外，指標的權重向量ω

根據拉格朗日函數，得到模糊識別模型如下

式中:uhj為樣本j對級別h的相對隸屬度，j=1，2，…，n;h=1，2，…，c。

級別特征值向量如下

4 應用實例

研究采用的數據為石家莊地區2004年地下水水質統測數據［9］。各評價指標分級標準見表1。

依據《地下水質量標準》(GB/T14848—93)，各評價指標分級標準見表2。

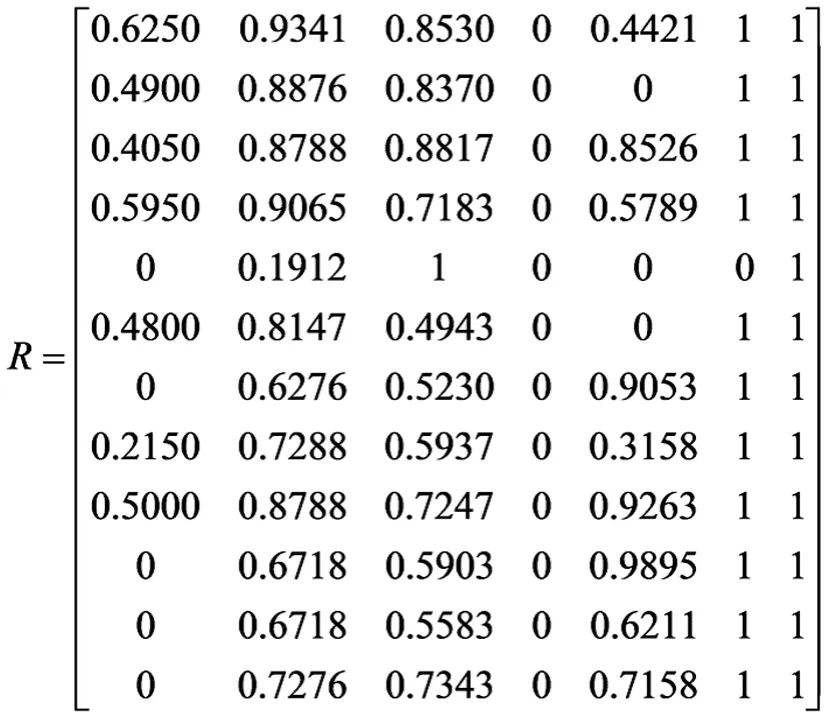
應用公式(5)將矩陣X變為相對隸屬度矩陣R為:

表1 研究區水質監測數據 mg/l

表2 地下水質量分級標準

應用公式(6)將矩陣Y變為指標標準特征值相對隸屬度矩陣S為:

根據二元比較方法，應用公式(2)得到7項指標二元比較矩陣如下:

根據上面矩陣，確定7項指標權重向量為:

運用模糊識別模型公式(8)得到水樣相對隸屬度矩陣U:

運用公式(9)得到各個樣本的級別特征值如下:

5 結論

從結論可以看出石家莊地區年地下水水質均處于Ⅱ－Ⅲ類中間，其中，井口5水質污染程度相對最為嚴重，井口1－b和14污染程度相對較為嚴重，井口40、1和2污染程度相對偏輕，井口26、66、15和70污染程度較輕，井口22和50污染程度最輕。文章應用二元比較方法確定指標權重以及模糊識別模型來進行地下水水質評價，方法比較簡便，物理概念清晰，根據相對隸屬度矩陣得到樣本級別特征值，直接進行評價分析，取得了較為理想的評價結果。

［1］中華人民共和國國家技術監督局.地下水質量標準GB/ T1448—93［M］.北京:中國標準出版社，1994:67.

［2］倪深海，白玉慧.BP神經網絡模型在地下水水質評價中的應用［J］.系統工程理論與實踐，2000(08):124－127.

［3］楊帆，張征，呂連宏，等.基于灰色關聯聚類的地下水評價指標優化研究［J］.環境工程，2008(26):304－309.

［4］王力，劉廷璽，戴鑫，等.基于熵權的模糊物元在地下水水質評價的應用［J］.人民黃河，2010，32(12):120－122.

［5］駱祖江，陸順.模糊綜合評判法在嵊泗海域地下水評價中的應用［J］.勘察科學技術，2009(04):51－54.

［6］歐亞波，李澤琴.地下水水質評價中相關性分析方法的應用［J］.廣東微量元素科學，2004，14(08):18－22.

［7］郭東興，劉運濤，楊曉雙，等.運用模糊數學法評價項城地下水水質［J］.地質災害與環境保護，2007，18(04): 105－107.

［8］邢軍，付芝，孫立波.基于熵權的地下水水質模糊綜合評價［J］.節水灌溉，2011(08):5－7.

［9］陳守煜.工程模糊集理論與應用［M］.北京:國防工業出版社，1998:26－28.