排管敷設電纜的載流量計算與優化排列

李攀峰，李春筱，馮 炳

（國網浙江省電力公司紹興供電公司，浙江 紹興 312000）

排管敷設電纜的載流量計算與優化排列

李攀峰，李春筱，馮 炳

（國網浙江省電力公司紹興供電公司，浙江 紹興 312000）

排管敷設是目前電力電纜的主要敷設方式，利用鏡像法和疊加原理,建立了排管敷設時電纜載流量的計算模型，運用推導出的公式計算雙回和四回排管敷設時每回電纜的載流量，給出了載流量最優的電纜排列方案。

電力電纜；排管；載流量；排列方式

地下電力電纜的敷設主要有土壤直埋、排管、溝槽和隧道4種方式，隨著城市電纜線路的日益增多，排管敷設逐漸成為電纜線路敷設的主要方式。當電纜多回路排管敷設時，不同相位排列方式，電纜的鄰近效應不同，計算出的載流量也不同，通過對電纜相位進行優化排列，可以降低鄰近效應的影響，從而提高電纜的載流量。

本文計算并比較多種排列方式下電纜的載流量，最終給出載流量最優的電纜排列方案。

1 計算假設條件

選取型號為YJLW03 64/110 kV 1×630 mm2的交聯聚乙烯絕緣波紋鋁護套縱向阻水中密度聚乙烯+聚氯乙烯雙護套電力電纜進行計算分析。該電纜由內向外依次為導電線芯、導體包帶、導體屏蔽層、絕緣層、外屏蔽層、墊包帶、皺紋鋁護套、外護套和手導電涂層，其結構尺寸見表1。電纜的敷設條件見表2。

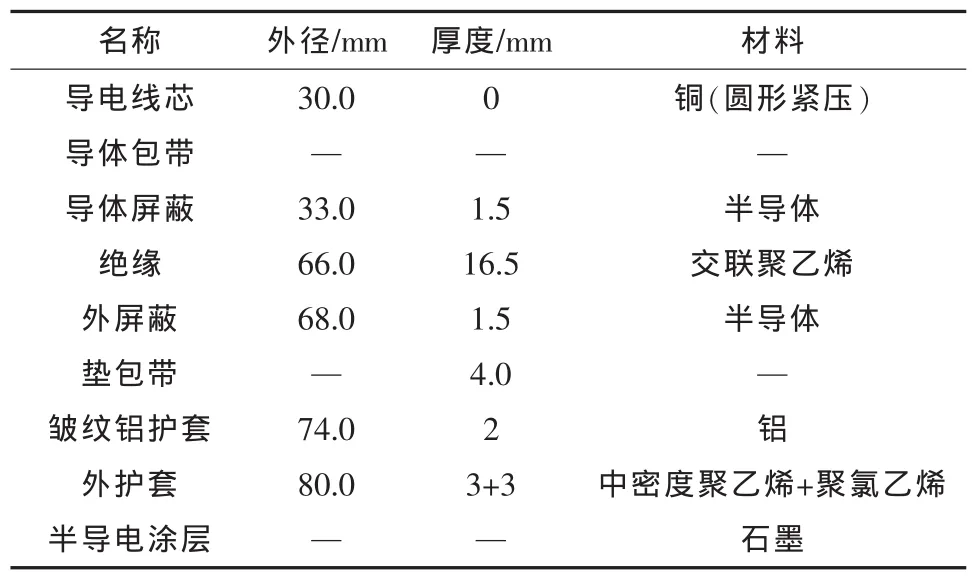
表1 電纜結構尺寸

表2 電纜使用環境條件

2 計算模型

2.1 載流量的計算公式

與其他敷設方式相比，除了絕緣熱阻、護層熱阻，電纜排管敷設時還應考慮管道中的外部熱阻，它主要由3部分組成，即電纜表面的管道內表面之間空氣熱阻、管道本身熱阻、管道外部熱阻。電纜排管敷設時，假設電纜護層中沒有電流，因電纜無鋼帶和鋼絲鎧裝，護層損耗可忽略不計；而電纜穿管埋設在水泥排管中，如果水泥有足夠的寬度和厚度，也不存在土壤中水分遷移問題，根據傳熱學原理，電纜的載流量計算公式可以簡化為：

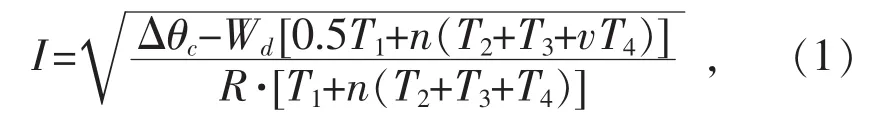
式中：v為干燥和潮濕土壤域熱阻系數之比率；R為最高運行溫度下導體單位長度的交流電阻；Δθc為土壤臨界溫升，即高于環境溫度的干燥與潮濕土壤邊界的溫升；Wd為導體絕緣介質損耗；T1為導體絕緣層的熱阻；T2為電纜外護層熱阻；T3為電纜表面與管道之間的熱阻；T4為管道中的外部熱阻。

式（1）中各參數，除T4外，其他僅與電纜的結構尺寸及其導體電阻有關，通過計算或查閱相關圖表可以求得，與電纜的敷設方式無關。

2.2 管道外部熱阻T4

T4不僅與外界敷設的方式相關，而且還涉及到其他電纜對被計算電纜的影響。因此，以下討論排管敷設下T4的計算。

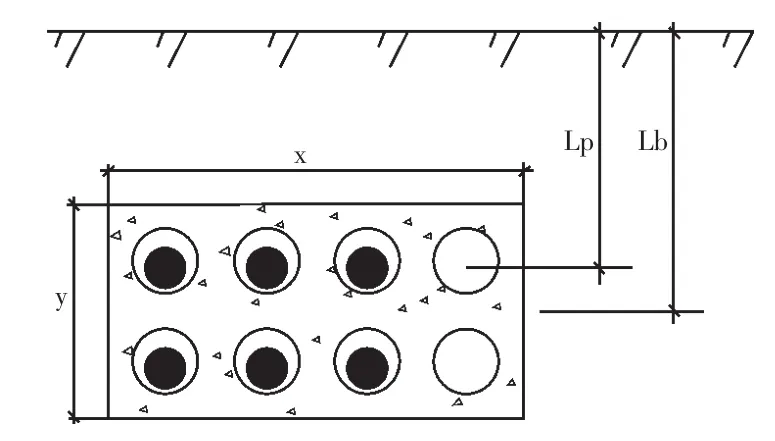
圖1 電纜敷設于排管混凝土模型

當排管嵌入混凝土中時，其熱阻由 2項組成：第一項假定管道外部全部為混凝土時的熱阻，但實際上一部分是混凝土，另一部分是土壤；第二項即考慮到實際情況的校正項。設定以電纜軸心為中心，以db直徑以外區域為土壤。db（僅對y/x≤3時有效）由式（2）給出：

語文新課標指出：語文這一門學科在與語言的應用上具有綜合性的同時還有實踐性。有了這樣的認識后，現如今的小學語文課正在逐漸發生改變，不再是以往空洞式的說教，現在開始重視對詞語的品讀，對句子的賞析，不再是死板地只學習書本上的知識，更重視課外拓展了，使語文教學回歸了本真。這種目的在于學生的語言能力，重點是在語言和文字的應用，通過進行語言文字扎實的訓練使語文回歸到本真，我們把這稱為“語用型教學”。本文對部編版三年級語文“語用型教學”措施展開分析，指出“語用型教學”的教學策略。

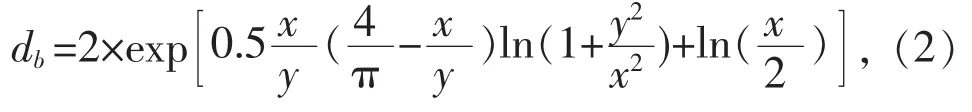
式中：db為混凝土包方的等效直徑；x為混凝土排管的寬度（與地面平行）；y為混凝土排管的高度（與地面垂直）。

混凝土包方深度即為混凝土圓柱體離地面距離Lb，則混凝土包方等效幾何因數為：

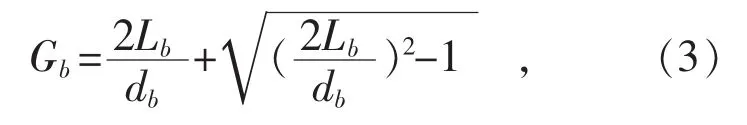
式中：Gb為混凝土包方的幾何因數，Gb在不同的x/y比值下近似拋物線。

按傳熱學原理，同時把土壤和水泥的熱阻看成均勻熱阻系數的介質，單根電纜管道以外的熱阻T4用鏡像法求得，其計算公式為：

式中：ρT為混凝土土壤熱阻系數。

當排管中敷設有多根電纜時，此時電纜管道外部熱阻T4需要考慮其他多根電纜發熱對某根電纜溫升的影響，可采用疊加原理，即多根電纜在某處產生的溫升（實際溫升）等于每根電纜在該處分別產生的溫升之和。假設排管電纜的數量為n，則水泥、土壤、電纜發熱對第k根電纜產生的溫升Δθk為：

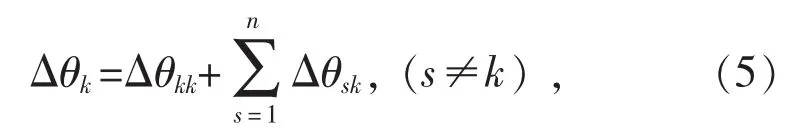
式中：Δθkk為第k根電纜本體發熱所產生的溫升；為其他電纜對第k根電纜產生的溫升。

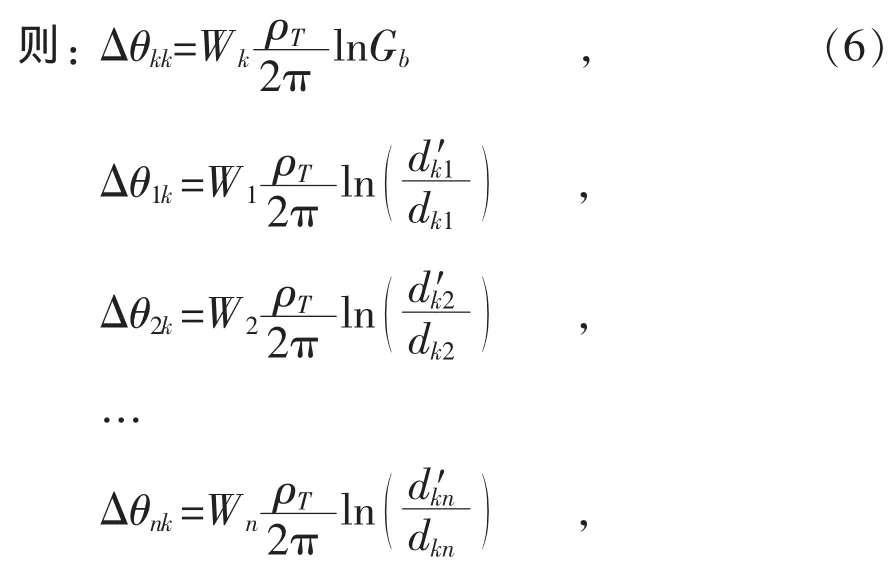
式中：W1，W2，…，Wn分別為第1，2，…，n根電纜的損耗功率；dkn為第n根電纜與第k根電纜間的距離為第n根電纜鏡像點與第k根電纜間的距離。假設排管中每根電纜的損耗功率相等，則：

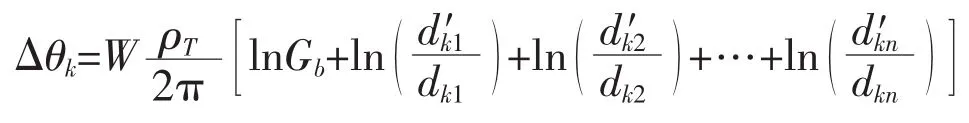
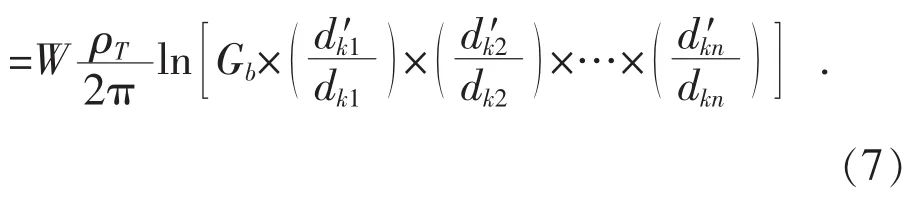
根據式（7）可以推出多根排管敷設時的電纜管道外部熱阻T4為：

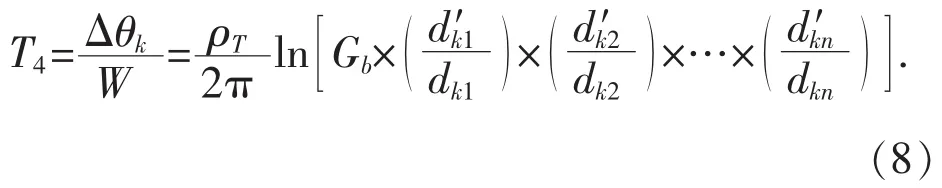
根據式（8）求出T4后，同時求出其他相關參數代入式（1），即可求出多根電纜排管時的載流量。

3 排列方式對載流量的影響

排管敷設時電纜的排列方式主要有“一”字形、三角形和垂直3種方式。“一”字形排列方式有利于散熱，但會產生電磁場的不平衡，特別是在雙端接地時，金屬套將產生較大的環流損耗；三角形排列不利于散熱，但電磁場比較平衡，對外電磁場影響較小。垂直排列時，也會產生電磁場的不平衡問題，同時下相電纜不易散熱。根據電纜在排管中敷設時載流量推導公式，分別計算雙回路和四回路電纜排管多種排列方式下的載流量，比較得出載流量最優的電纜排列方案。

3.1 雙回路電纜排列方式對載流量的影響

雙回路排管按8+2孔布置，其中6孔為電纜孔，2孔為電纜故障備用孔，2孔為電纜回流孔，選取了排管敷設的6種電纜回路排列方案，如圖3所示。

圖3 雙回路排管6種排列方案

在單端接地方式下，計算得出的載流量如表3所示。由表3可看出：方案一的載流量最大，電纜電磁場較平衡，倒置的三角形布置使下相電纜散熱影響降至最小，而且雙回路之間電磁場互不干擾，損耗最小；除方案五外，其他方案載流量大致相當，但由于受回路之間的電磁場影響及埋設深度增加，載流量均比方案一小。故在雙回路排管敷設時，從載流量最大的角度考慮，推薦兩個倒置三角形水平布置，即方案一。

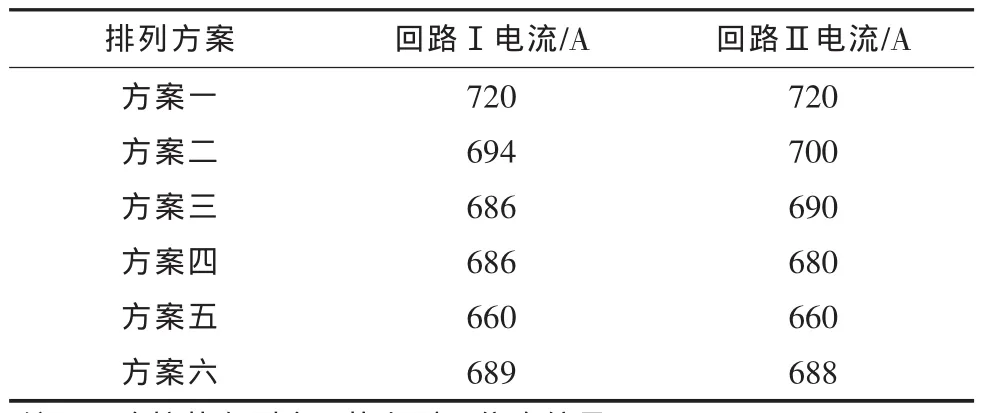
表3 雙回路電纜排管6種排列方案下的載流量

3.2 四回路電纜排列方式對載流量的影響

四回路排管按14+4孔布置，其中12孔為電纜孔，2孔為電纜故障備用孔，4孔為電纜回流孔。本文選取了四回路排管敷設的5種電纜回路排列方案，如圖4所示。

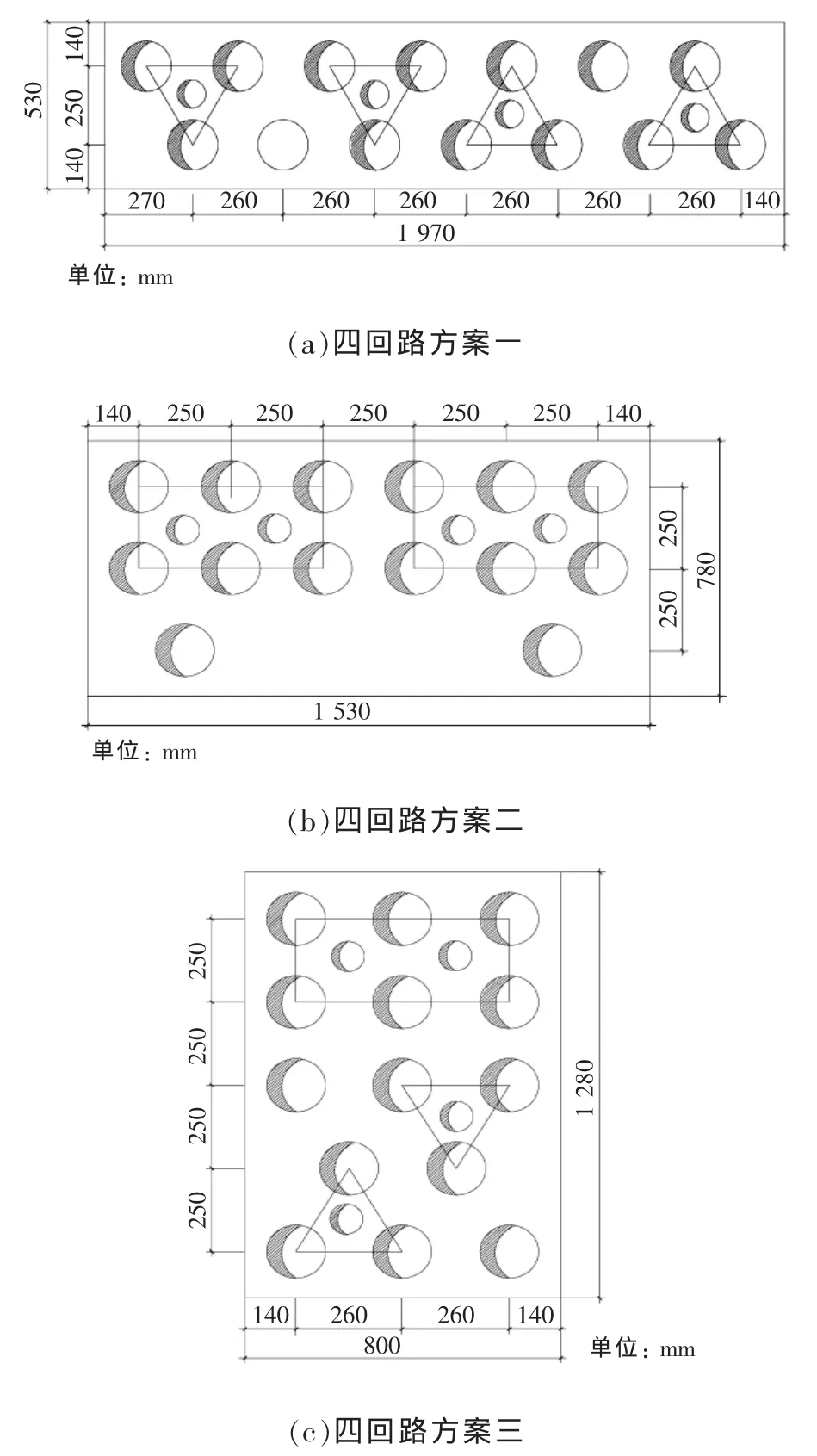
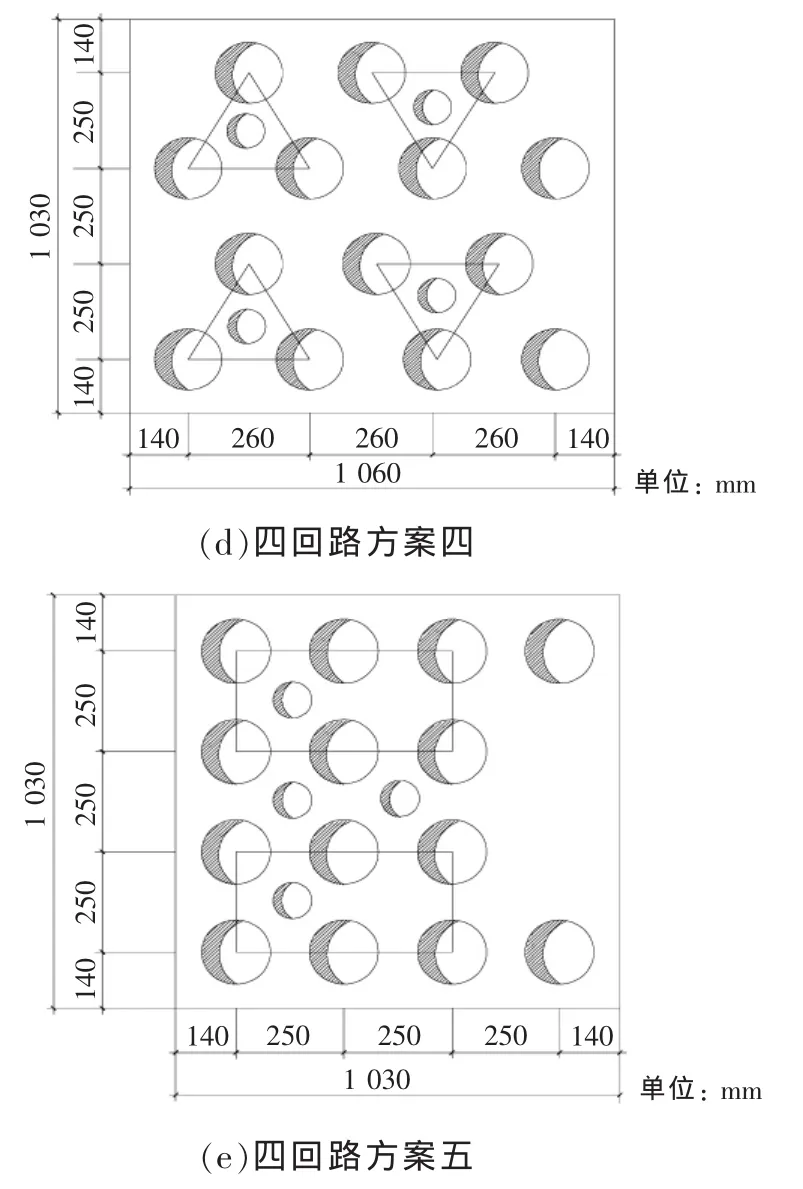
圖4 四回路電纜排管5種排列方案

在單端接地方式下，計算得出的載流量如表4所示。從表4可以看出，與雙回路敷設時比較，當多根電纜密集敷設時，多回路電纜將產生電磁和熱的相互影響，因而損耗將增大，散熱效果差，載流量將隨回路數的增多而減小。當電纜采用四回水平三角形排列時（方案一），電纜載流量最大，主要因為三角形排列時電磁場較為均勻，回路之間影響小，且單層布置因埋深小而散熱性能好，但此方案對電纜的通道寬度要求高，在路徑緊張區域難以實施。方案二中電纜均為水平排列，相對方案一每回電纜載流量減少5.1%，但該方案對電纜通道寬度要求僅為1.5 m，實用性強。

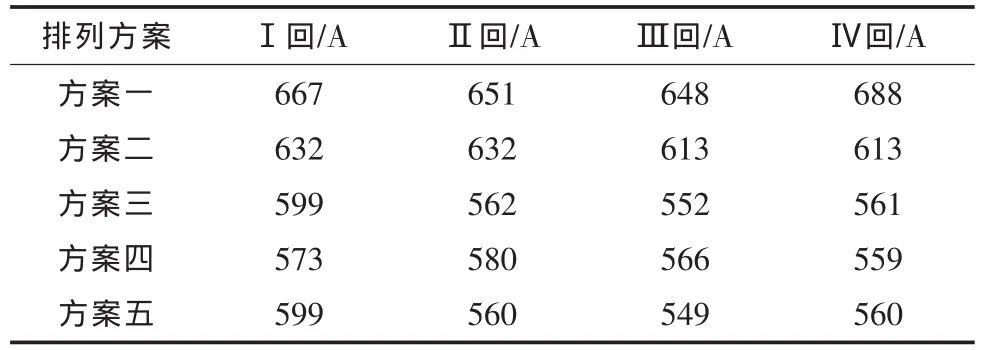
表4 四回路電纜排管5種排列方案下的載流量

當四回路電纜采用方案五中“一”字形垂直排列方式敷設時，載流量最大為599 A，較雙回路敷設時（686 A）下降了將近13%，且第二、三層下降更多，主要是由于電纜回路之間電磁場影響加大，造成電纜損耗增加，同時四回路垂直布置散熱性能較差，載流量必然受影響。受上下相鄰回路及電纜敷設深度影響，方案三與方案五載流量相當。方案四載流量最小。

故在四回路排管敷設時，從載流量最大的角度考慮，當路徑通道寬度允許時，推薦方案一，其次為方案二；在通道緊張區域，宜采用方案五。

4 結論

（1）利用鏡像法和疊加原理，建立了排管敷設時電纜載流量的計算模型，重點論述了管道外部熱阻T4的計算方法，推導出了排管中電纜載流量的計算公式。

（2）分別計算了雙回路和四回路電纜排管敷設時多種排列方式下的載流量。在雙回路排管敷設時，推薦2個倒置三角形水平布置，即方案一，此方案載流量最大。在四回路排管敷設時，從載流量最大的角度考慮，當路徑通道寬度允許時，推薦方案一，其次為方案二；在通道緊張區域，宜采用方案五。

[1]馬國棟．電線電纜載流量[M]．北京：中國電力出版社，2013．

[2]周炳凌，范玉軍，甘則富，等.排管敷設情況下電纜額定載流量研究之二——載流量計算[J].電線電纜，2008（2）∶26-30.

[3]賈欣，曹曉瓏，喻明.單芯電纜計及護套環流時載流量的計算[J].高電壓技術，2001（1）∶25-26.

[4]王增強，曹惠玲.預埋管地下電纜溫度場和載流量的數值計算[J].河北工業大學學報，2003（3）∶32-33.

[5]于景豐.電力電纜實用新技術[M].北京：中國水利水電出版社，2014.

[6]梁永春，孟凡鳳，王正剛，等．土壤直埋電纜群額定載流量的計算[J].高壓電器，2006，42（4）∶244-246．

[7]梁永春，李彥明，柴進愛，等.地下電纜群穩態溫度場和載流量計算新方法[J].電工技術學報，2007（22）∶185-190.

（本文編輯：方明霞）

Ampacity Calculation and Optimized Arrangement of Cables in Ducts

LI Panfeng，LI Chunxiao，FENG Bing
（State Grid Shaoxing Power Supply Company，Shaoxing Zhejiang 312000，China）

Duct is one of the main laying methods of power cable，A model for calculation of the ampacity of cables installed in ducts is established by the mirror method and superpos ition principle in this paper；by use of deduced formula，ampacity of cables in the double and four-trow ducts is calculated.The paper also puts forward the optimal arrangement scheme of cable.

power cable；duct；ampacity；arrangement mode

TM757

B

1007-1881（2015）12-0019-05

2015-05-05

李攀峰（1983），男，工程師，從事輸電線路設計工作。