小學數學習題設計需注重三個方面

江蘇揚中市聯合中心小學（212200） 王 琴

習題設計在數學教學中的功效不言而喻，一方面可考查學生對知識的掌握情況，另一方面能培養學生對數學思想方法的靈活運用能力。在小學數學習題設計中，不論是化抽象為形象，還是化新知為舊知，教師習題設計的核心，都是要能夠綱舉目張、舉一反三，促進學生的數學思考，發展學生的數學思維。現以“平均分”這一概念為例談談小學數學習題設計需注重的三個方面。

一、注重針對性，指向知識核心

習題設計的本質，是要能夠強化學生所學知識，并將所學知識拿來熟練運用，突破學習的難點，解決數學問題。因而，教師要將習題設計的重心放在學生容易迷惑的地方，越是認知模糊，越是需要加強習題訓練，由此突破數學難點，直指知識核心。

例如，在學生學完《分數的意義》之后，對“平均分”這個關鍵概念仍然沒有建構深刻認知，還停留在淺層次上。為此，我設計了這樣一道習題：一根繩子長5米，分成6段，每段繩長占幾分之幾？學生在做這道題時，認為繩子的長度除以6，就是每段繩子占總繩長的幾分之幾。結果整個班級幾乎“全軍覆沒”。此時我讓學生思考：想一想，題目中說將繩子分為6段，從這里你知道了什么？很快有學生反應過來，指出題目中的條件是“將繩子分為6段”，并沒有標明平均分，因而這個題目給出的已知條件并不充分，也就沒法進行解答。此時，我引導學生反思：你有什么教訓？得到了什么啟示？學生認為，自己忽略了“平均分”這個重要條件，由此從錯誤中獲得深刻認知，明確了平均分在分數中所占據的重要地位。

二、注重綜合性，溝通新舊知識

數學家華羅庚指出，讀書的第一層境界是要將書讀薄，將知識吸收拓展，內化成為自己的技能，書就可以扔掉了。對于習題設計來說，也應當如此。教師應將宏觀和微觀的教材都統合起來，溝通學生所學的新舊知識，將散落的知識由點到面，串成線、連成片，構建系統化的知識體系，將教材讀薄讀透，由此提升學生的數學思維。

例如，在第一次習題設計中，學生對“平均分”這個字眼有了敏感度，那么，是否學生就對平均分有了深刻認知呢？我緊接著又設計了一道習題：如圖1，A、B兩點分別是三角形兩條邊的中線，陰影部分的面積占三角形面積的幾分之幾？（ ）。法解答

學生認為，這里沒有“平均分”的字眼，因而不能判斷陰影部分面積占三角形的幾分之幾，此時我追問：再仔細讀讀題中條件，你發現了什么？學生經過仔細觀察，發現隱藏著潛在的“平均分”：A、B兩點是兩條邊的中線，假設C是底邊的中點，那么可以再添加一條輔助線（如圖2），這樣就將三角形平分成了4等份，陰影部分的面積就是其中的一份，由此可以得到1/4。此時我繼續引導：如果不用輔助線，運用我們學過的知識，怎么解答呢？學生認為，根據學過的“圖形的放大和縮小”，大三角形是根據每條邊2∶1的比例，將陰影部分放大，因而大三角形的面積是陰影部分三角形的4倍，由此可以得到陰影部分面積是大三角形面積的1/4。

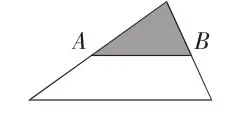
圖1

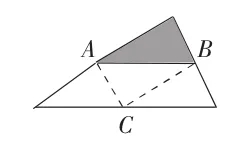
圖2

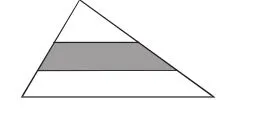
圖3

以上習題設計，突破了數學習題中的表征形式，為學生學習后續的知識積累了經驗，提升了學生的數學思維能力。

三、注重思維性，發展推理能力

教學中，常常有教師設計大量習題，目的是讓學生提升技能，其實這種做法的最大誤區在于，忽略了習題的思維性。練習的目的是為了提高思維能力，讓學生從直觀到抽象，逐步提升。

例如，針對“平均分”這個概念，學生如果只是掌握了內涵還遠遠不夠，還需要教師設計相關練習，讓學生深入其中，理解并體驗它的外延。為此，我設計了第三道習題：如圖3，將三角形的兩條邊分別三等分，陰影部分面積占原來三角形面積的（ ）。法解答

學生基于上一道習題的經驗，很快透過不平均的外表找到了隱藏在其中的“平均分”：三角形的兩條邊三等分，學生由此根據圖形的放大和縮小的數學模型，展開演繹推理，將陰影面積和兩個三角形面積建立聯系，從而推算出陰影部分面積和整個大三角形面積的比為1/3。通過以上習題設計，學生不但獲得了深刻的洞察力，而且大大提升了邏輯推理能力，發展了數學思維。

總之，在小學數學教學中，教師的習題設計不能盲目貪多，而是要精煉，具有針對性、綜合性和思維性，這也是每道習題設計的精髓所在。