一種基于雙精度搜索算法的變論域模糊控制
劉培奇,田 洋,孫陽陽
LIU Peiqi,TIAN Yang,SUN Yangyang
西安建筑科技大學 信息與控制工程學院,西安710055
College of Information&Control Engineering,Xi’an University of Architecture&Technology,Xi’an 710055,China
1 引言
相對于傳統控制方式,模糊控制(FC)憑借其不需對象模型、魯棒性強、實時性好等優點廣泛用于非線性、時變滯后系統中。然而模糊控制器實質上是插值器,插值精度與模糊規則數量緊密相關,提高精度必然以擴大規模為代價,導致其控制精度存在一定局限性[1]。變論域模糊控制器(VUFC)不僅可以綜合專家知識,而且在不增加規則數量的情況下,論域隨誤差變小而收縮并隨誤差增大而擴展,從一定程度上解決了控制精度和控制復雜度的矛盾[2]。理論上分析,VUFC 的決策速度與精度應相對理想,可伸縮因子的定式結構使其自適應能力有限,控制無法達到預期效果[3]。同時模糊系統基本處于黑箱狀態,被控對象多具有高度的非線性、強耦合等特性,因此定式伸縮因子很難有效避免控制函數畸變產生,盡管在控制精度上有較大提高,但卻無法保證控制品質的最優性[4]。在模糊規則確定好的情況下,僅通過系統狀態來調節VUFC 伸縮因子,必然使其因調節負擔過重而不能得到理想輸出。
近年來,VUFC 參數優化問題受到人們的關注,這也成為改善VUFC 精度和控制函數畸變的最有效方法,許多智能優化算法在這一研究中得到廣泛應用。文獻[5]利用遺傳算法(GA)優化VUFC 的部分參數,但GA要進行復制、交叉和變異操作,不能及時利用網絡的反饋信息,算法的搜索速度慢,且其性能對參數有較大依賴性。文獻[6]提出一種基于粒子群算法(PSO)的變論域模糊控制策略,但PSO 種群在搜索空間中多樣性的丟失使算法不夠穩定,不是每次所得結果都能收斂到一個點。文獻[7]通過引進具有在線學習和動態尋優能力的Q 學習算法(Q-learning)達到使控制器性能指標最小的目的,但Q-learning 學習時間較長,時間和空間復雜度相對較高。引力搜索算法(GSA)利用物體間的萬有引力定理搜索最優解,是一種相對穩定的全局搜索算法,已成功實現參數辨識并應用于流程優化。本研究結合VUFC參數優化復雜度指標,在GSA 基礎上結合序列二次規劃搜索(SQP),提出一種雙精度搜索算法。該算法在保留GSA 極強全局尋優能力基礎上,進一步提高算法對最優解的局部搜索能力,并將改進算法用于等比因子智能尋優,構成一種基于雙精度搜索算法的變論域模糊控制器。其目的是在減小伸縮因子調節負擔的同時使控制函數畸變問題得到優化,進一步提高決策速度和控制效果。
2 控制算法基本原理
2.1 變論域模糊控制器
設雙輸入變量誤差e和誤差變化率ec的論域分別為X=[-E,E]、Y=[-EC,EC],控制輸出變量u論域為Z=[-U,U],對應的語言變量為A、B、C且[8]:
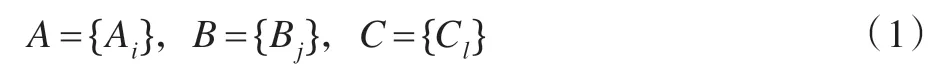
式(1)是對論域X、Y、Z的模糊劃分,xi、yj、zl分別是Ai、Bj、Cl的峰點,其中i=1,2,…,n,j=1,2,…,m,l=1,2,…,mn,并設定Ai、Bj、Cl均為可積函數。
由模糊推理規則可得到以下推理形式:
IfxisAi,andyisBj,thenuisCij.
其中i=1,2,…,n,j=1,2,…,m。
模糊控制系統可以表示成一個n元插值函數:
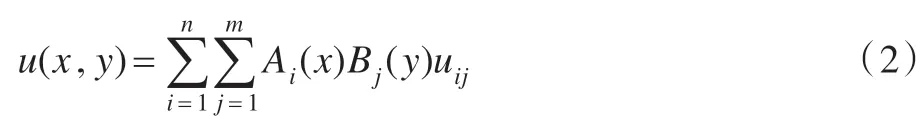
其中i=1,2,…,m,j=1,2,…,n。
變論域模糊控制實質是采用“粗略控制”到“精細控制”的策略,即當模糊控制器的輸入(一般為誤差E)較大時,采用“粗略控制”,論域隨之膨脹;當模糊控制器輸入較小時,采用“精細控制”,論域隨之壓縮。變化后的論域可以表示為:
X(e)=[-α1(e)E,α1(e)E]
Y(ec)=[-α2(ec)EC,α2(e)EC]
Z(e,ec)=[-β(e,ec)U,β(e,ec)U]
其中α1(e)、α2(ec)和β(e,ec)叫作論域的伸縮因子,e、ec都是時間函數,相對于變論域,原來的論域X、Y、Z叫作初始論域,基于式(2)的變論域模糊控制可以表示成如下n元動態插值函數:
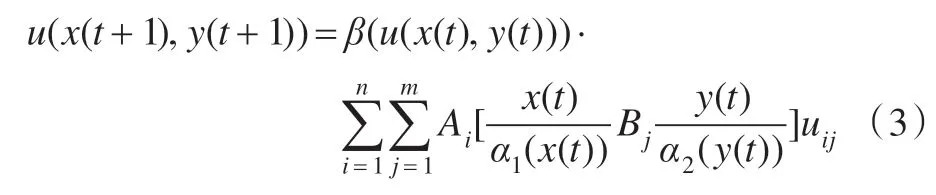
變論域模糊控制器較模糊控制器在自適應能力、控制精度等性能方面都得到了提升,并且變論域模糊控制器的控制規則的設計更為簡單,它無需太多的專家知識和經驗,只需要獲取規則的大致趨勢即可[9]。
在模糊規則設計好的情況下,對變論域模糊控制要求的關鍵部分在于輸入、輸出論域伸縮因子選擇,輸入、輸出論域伸縮因子本文選擇[10-11]:
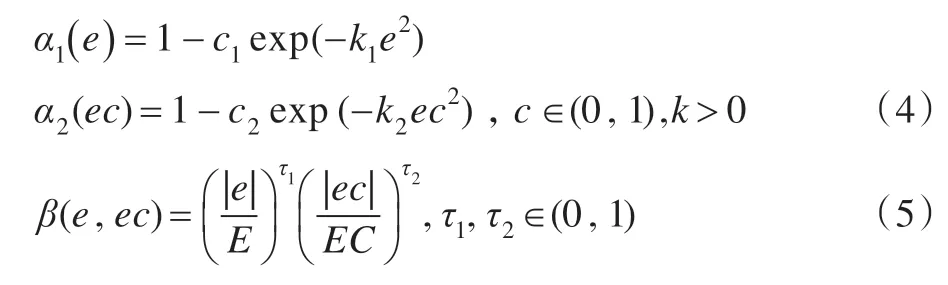
2.2 雙精度搜索算法
GSA 是基于對群體的物理學萬有引力進行模擬而提出的新的優化搜索技術,它通過群體中各粒子間的萬有引力相互作用智能指導搜索結果[12]。研究發現,GSA具有較好的全局優化能力,但局部搜索能力較差,在迭代的早期,算法具有較好的尋優性能,但在后期會出現在局部最優解附近“振蕩”的現象,趨同化嚴重,易早熟。SQP 是軌跡優化中應用較為廣泛的一種約束非線性優化算法,其收斂速度快,可靠性高,國內外許多大型優化軟件都是基于該算法編寫的,但該算法需要一個較好的初始點[13]。本研究結合兩者特點,首先利用GSA 的全局搜索能力進行初始優化,將優化結果提供給SQP 作為初始點,這種串行優化策略結合了GSA 和SQP 的優點,具有較強的全局和局部搜索能力,同時算法的計算速度和精度都有明顯提高。在改進算法中,由于采用“全局-局部”雙重精度的搜索機制,因此定義為雙精度搜索算法(Double Precision Search Algorithm,DPSA)。算法流程如圖1 所示。
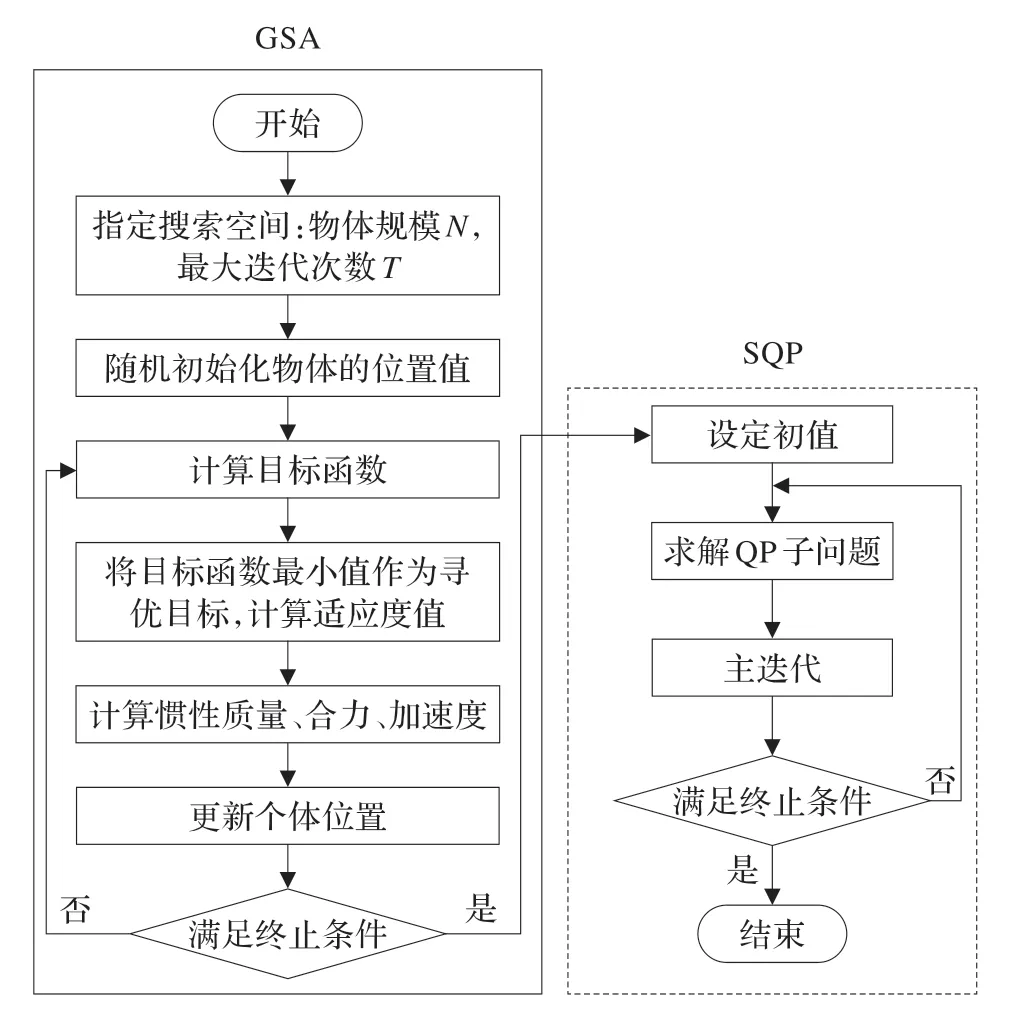
圖1 算法流程圖
3 基于雙精度搜索算法的變論域模糊控制
3.1 等比因子
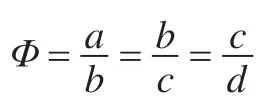
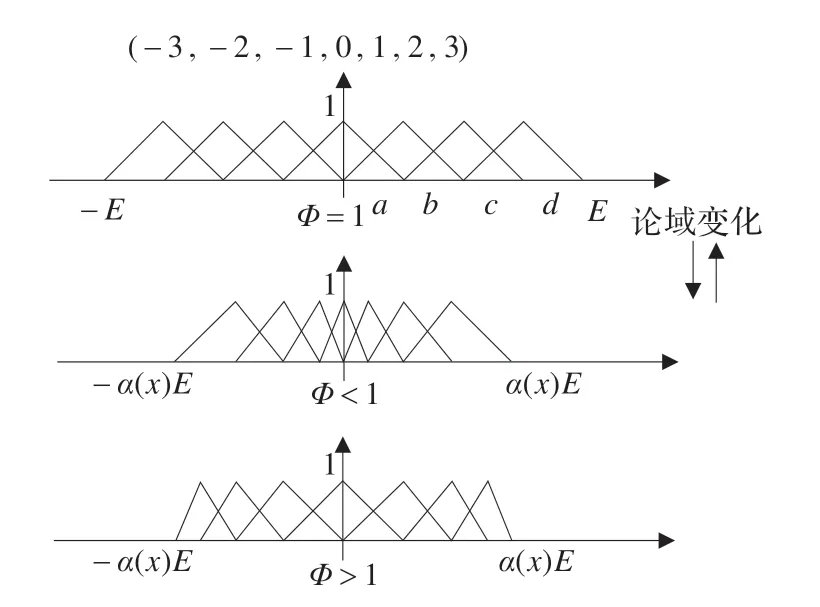
圖2 不同Φ 值時不同形式的隸屬度函數
3.2 性能指標
VUFC 參數優化是一類特殊的優化問題,需要采集系統輸入輸出數據構建目標函數。目標函數的選取對優化問題求解極為關鍵,必須準確反映優化目標。對于控制系統參數優化問題,目標函數的構建以獲取最優控制性能指標為依據。控制理論中常見的指標有絕對誤差積分指標IAE、平方誤差積分指標ISE、時間平方誤差乘積積分指標ITSE和時間絕對誤差乘積指標ITAE。ITAE指標與其他幾類指標相比能更好反映系統控制品質[15-16],ITAE指標目標函數離散形式定義為:
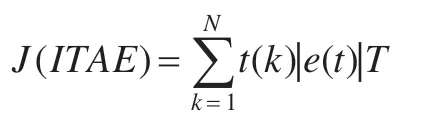
3.3 控制器設計與分析
利用DPSA 和VUFC 各自的優勢,設計基于雙精度搜索算法的變論域模糊控制器(DPSA-VUFC),系統結構如圖3 所示。
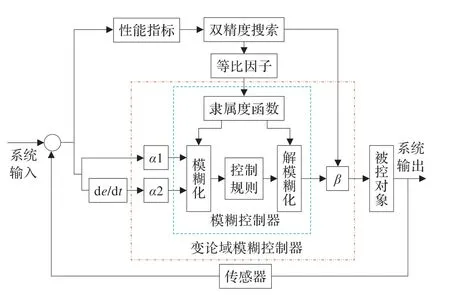
圖3 基于雙精度搜索算法的變論域模糊控制結構圖
在本設計中,用變論域模糊控制器中的伸縮因子調節論域大小進行外調節,而等比因子無法改變論域大小進行內調節,內外結合。這樣的設計后,等比因子調節不但減輕了伸縮因子的調節負擔,而且當在變論域過程中由于隸屬度函數發生改變,以致輸出控制函數發生畸變時,表現為外部性能指標ITAE變大,等比因子就會配合調節,迫使指標變小。
目標函數變量及優化變量為VUFC 等比因子Φ,DPSA 通過在解空間中搜索調整Φ值來獲得目標函數最小值,從而求取最優Φ值。當J(ITAE)值較大時,即誤差e較大,為使誤差e快速進入穩定區域,論域應進行一定的擴展,等比因子應該配合伸縮因子快速粗調,即Φ>1;當J(ITAE)值較小時,誤差e接近穩定區域,為了提高控制精度,減少模糊集峰點之間的距離即論域收縮的同時,等比因子配合伸縮因子細調節,即Φ<1。
定式變論域模糊控制相當于保持等比因子不變,只調整論域的大小,而等比因子無法調整論域大小,卻可以調節隸屬度函數,兩者結合使用起到互補的效果,可使模糊控制器的性能接近最優。
4 算法仿真
同步發電機勵磁控制系統在穩態和暫態過程中都會直接影響發電機的性能,優良的勵磁系統不僅可以保證高質量的電能、發電機運行可靠性和穩定性,而且可以有效地提高發電機及其相關電力系統的技術經濟指標。勵磁控制系統由放大單元、勵磁機、同步發電機、測量傳感器和變論域模糊控制單元組成,其模型可用圖4傳遞函數框圖表示[16-17]。其中K為各環節放大系數,V為環節輸出,τ為時間常數,Vo為系統輸出即為機端電壓。
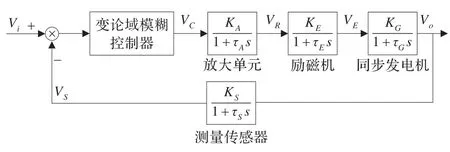
圖4 勵磁控制系統傳遞函數框圖
4.1 系統參數設置
超調作為勵磁系統動態控制過程中最重要的指標,能直接反應控制系統的穩定性。本實驗采用綜合考慮ITAE指標與超調量的目標函數來獲得更優的控制品質:
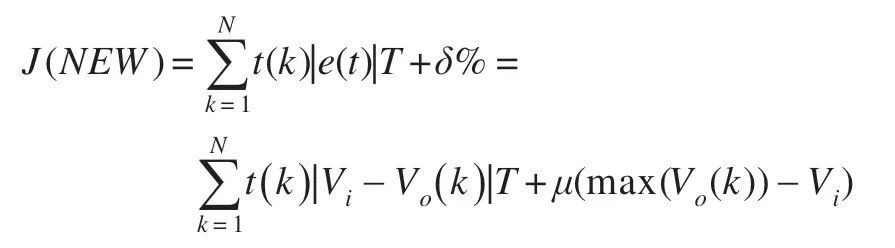
等式右邊前一項為指標ITAE,后一項為超調量;μ為相對權重參數。
為了驗證DPSA-VUFC 控制方法的有效性,進行同步發電機勵磁控制系統的Matlab仿真實驗,模型如圖4所示,參數設置:KA=10,τA=0.1,KE=1,τE=0.5,KG=0.6,τG=1,KS=1,τS=0.01。
仿真系統實驗按照本文設計優化策略和算法進行。分別采用GA、PSO 和DPSA 作為優化器,搜索目標函數。GA 參數:種群規模N=40,迭代次數n=500,交叉率Pc=0.7,變異率Pm=0.05;PSO 參數:種群規模N=40,迭代次數為n=500,c1=c2=2。DPSA 參數:種群規模N=30,G0=20,α=1,c1=c2=0.5。
VUFC對于輸入量e和ec,基本論域為[-60,60]和[-10,10],對于所有輸入輸出變量的離散論域都為[-6,6]。變論域采用將量化因子Ke、Kec分別除以對應伸縮因子,比例因子Ku乘以對應的伸縮因子的等價處理辦法:Ke=6/60=0.1,Kec=6/10=0.6,Ku=1。相應模糊集{NB,NM,NS,ZO,PS,PM,PB},控制決策表如表1 所示。伸縮因子依式(4)、(5),參數取為:c1=0.5,c2=0.8,k1=1.0,k2=1.5,τ1=0.3,τ2=0.9。控制器采用三角形隸屬度函數,并采用加權平均法將模糊量精確化。
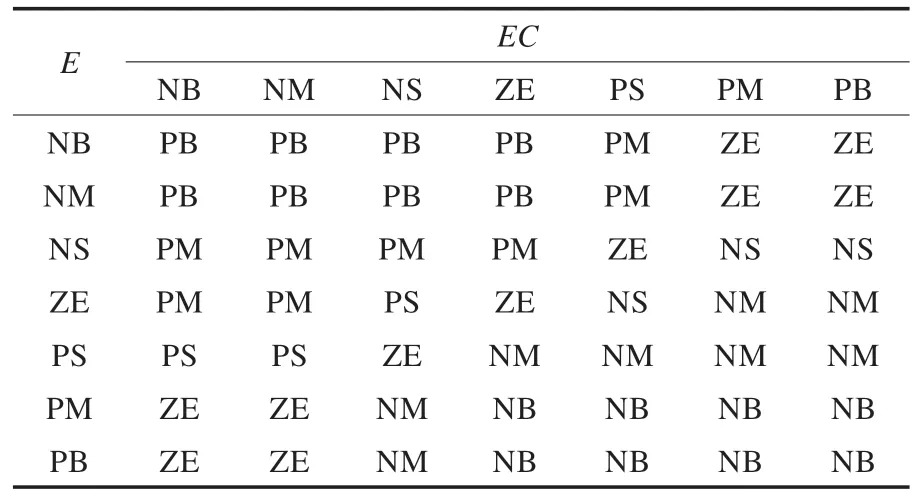
表1 模糊控制規則表
4.2 實驗結果分析
考慮到算法的隨機性,為了達到測試結果的穩定,對于給定模型,每個算法獨立運行 20 次取其統計結果,包括最小值、最大值、平均值和標準差,每次的初始點均由計算機隨機產生。統計數據表2 為20 次重復實驗不同優化方法獲得的最優目標函數值統計結果,表3為對應超調量統計結果。
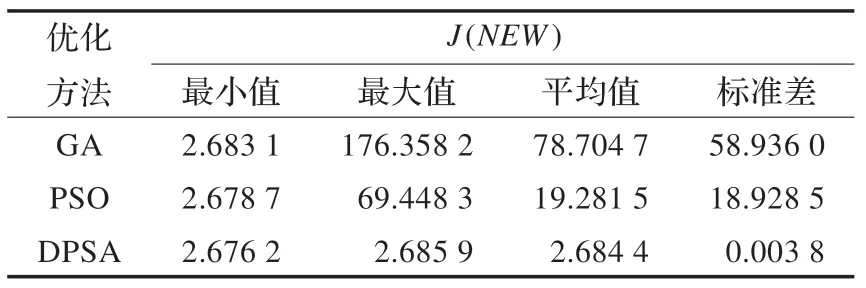
表2 不同優化方法所得最優目標函數值
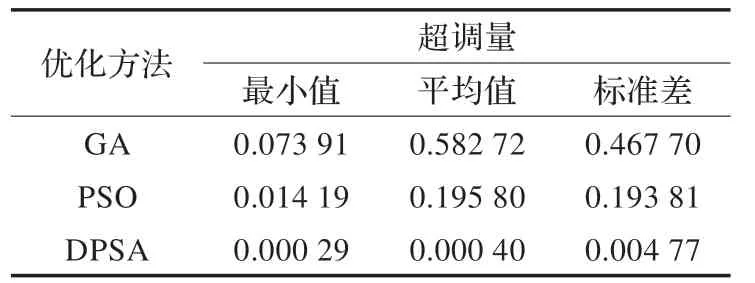
表3 不同優化方法所得超調量
分析表2 可知,DPSA 得到的最優目標函數最小值和最大值大小基本相等,而GA 和PSO 最優目標函數最小值和最大值大小相差大,較DPSA,GA 的差距甚至達到了102數量級,并且DPSA 最優目標函數平均值和方差兩項指標明顯小于其他兩種方法。通過比較20 次計算的均值可以發現,DPSA 均值幾乎與最優值相同,而GA 和PSO 均值與最優值有不小的差距。因此DPSA 得到的最優目標函數結果顯現出明顯的優勢,表明其在方法的穩定性上表現突出。由表3 可知,DPSA 得到的超調量平均值和標準差明顯小于GA 和PSO,進一步說明其在尋優過程中的穩定性更好。
圖5 和圖6 為3 種不同控制方式搜索20 次獲得的等比因子Φ對應的調節過程仿真曲線。其中圖5 為20 次結果中最優Φ值對應的調節過程,圖6 為平均最優Φ值對應的調節過程。兩組仿真曲線表明,采用DPSA-VUFC控制方式在快速性、準確性上都優于其他兩種控制方式,超調量極低且穩定性最好。GA 和PSO 在兩組實驗中表現不夠滿意,是由于算法本身穩定性不夠造成的。20 次重復實驗中,部分優化結果效果良好,部分結果效果較差,從而影響了算法在參數尋優中的整體表現。而DPSA 穩定性高,優化效果平均,超調極小,幾乎沒有震蕩,當收斂后即尋優結束后,能夠快速進入穩定區。
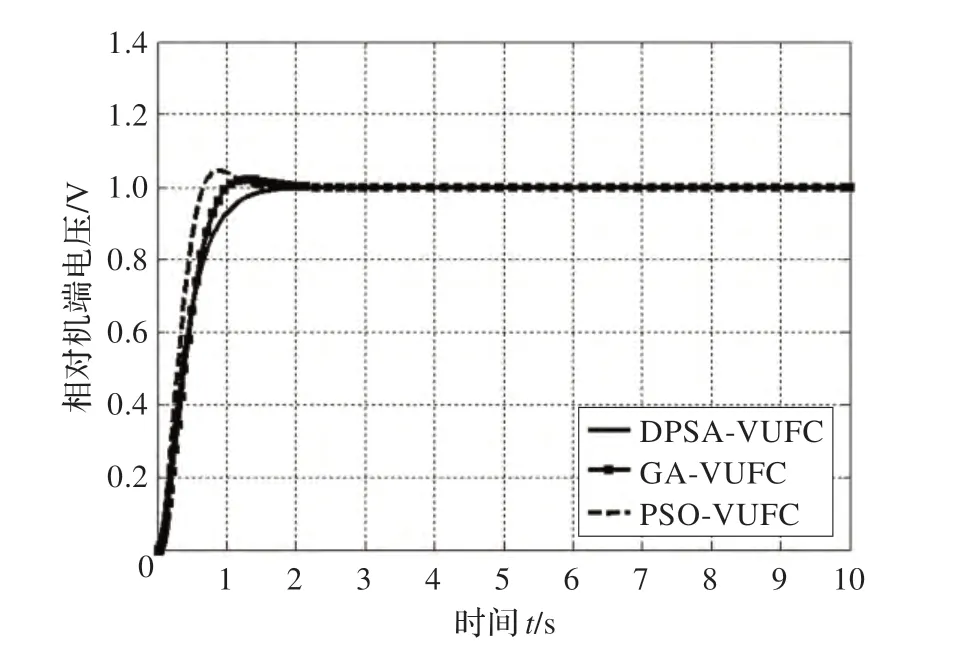
圖5 最優Φ 值對應的調節過程
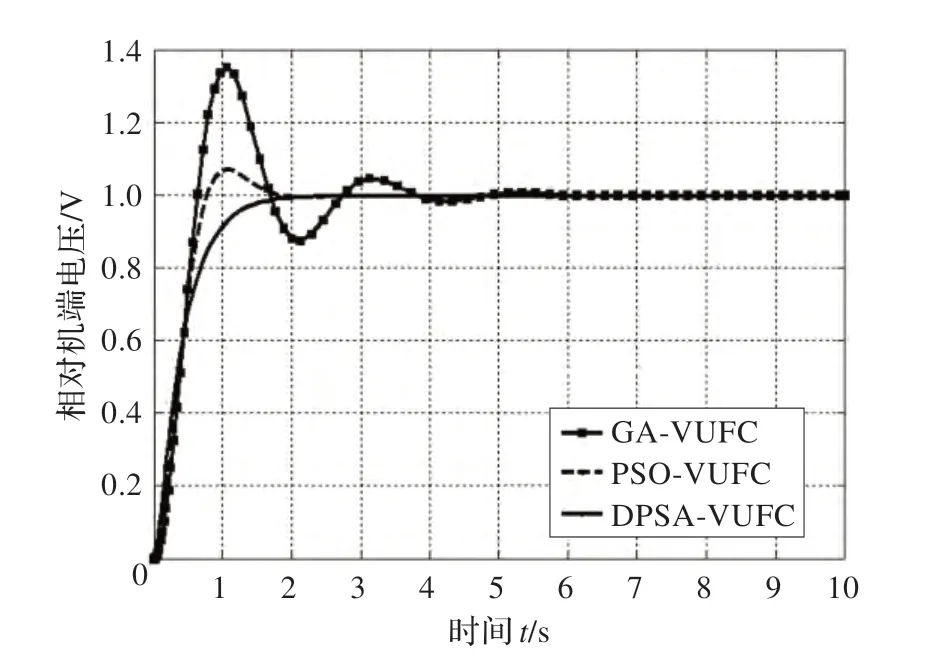
圖6 平均最優Φ 值對應的調節過程
5 結束語
本文針對定式變論域模糊控制器伸縮因子控制壓力大,控制函數在遺傳復制中由于隸屬度函數變化引起輸入輸出的變化等缺點,設計了基于雙精度搜索算法的變論域模糊控制器。通過伸縮因子自適應調整模糊控制器論域,從而在不增加模糊控制規則的前提下使控制精度提高,而等比因子的調節分擔了伸縮因子的調節負擔,極大程度上克服了由于隸屬度函數變化問題所帶來的對控制器動態性能的影響。對比實驗表明DPSA在參數尋優中的搜索能力明顯優于其他兩種算法且穩定性高,同時DPSA-VUFC 控制方式的收斂速度快,上升和調節時間短,其J(NEW)統計值也非常小,控制效果較其他兩種控制方式都要理想。作為一種新型優化搜索算法,DPSA 具備在VUFC 參數優化中深入應用的潛力。
[1] Cheng Chibin.Fuzzy process control:construction of control charts with fuzzy numbers[J].Fuzzy Sets and Systems,2005,154(2):287-303.
[2] Mann G,Gosine R G.Three-dimensional min-max-gravity based fuzzy PID inference analysis and tuning[J].Fuzzy Sets and Systems,2005,156(2):300-323.
[3] 李洪興.變論域自適應模糊控制器[J].中國科學:E 輯,1999,29(1):32-42.
[4] 李洪興.非線性系統的變論域穩定自適應模糊控制[J].中國科學:E 輯,2002,32(2):211-223.
[5] 肖磊,張阿卜.一種基于遺傳算法的新的模糊控制器優化方法[J].控制理論與應用,2005,24(10):1-3.
[6] 彭靈志.基于粒子群算法變論域的模糊控制策略研究及其應用[D].長沙:中南大學,2005:1-60.
[7] 余濤,于文俊,李章文.基于Q 學習算法的變論域模糊控制新算法[J].控制理論與應用,2011,28(11):1645-1650.
[8] 諸靜.模糊控制理論與系統原理[M].北京:機械工業出版社,2005:212-214.
[9] Chen P C,Hsu C F,Lee T T.Fuzzy-identification-based adaptive back stepping control using a self-organizing fuzzy system[J].Soft Comput,2008,13(22):635-647.
[10] 邵誠,董希文,王曉芳.變論域模糊控制器伸縮因子的選擇方法[J].信息與控制,2010,39(5):536-541.
[11] 趙云濤,王京,謝新亮,等.基于多層蟻群算法的變論域模糊控制[J].模式識別與人工智能,2009,22(5).
[12] Rashedi E,Nezamabadi-Pour H,Saryazdi S.GSA:a gravitational search algorithm[J].Information Sciences,2009,179(13):2232-2248.
[13] 付磊,安效民,覃曌華,等.基于混合遺傳算法的多沖量最優變軌[J].航天控制,2013,31(3):15-19.
[14] 李家煒.一種新的優化模糊控制器算法[J].控制理論與應用,2002,19(2):279-281.
[15] Ogatt K.Modern control engineering[M].Upper Saddle River,NJ:Prentice Hall,1990.
[16] 李超順,周建中,肖劍.基于改進引力搜索算法的勵磁控制PID 參數優化[J].華中科技大學學報:自然科學版,2012,40(10):119-122.
[17] IEEE Power Energy & Society.IEEE Std421.1-86 IEEE standard definition for excitation systems for synchronous machines[S].Piscataway:IEEE Press,1986.

