基于PWM 思想的深度腦刺激波形成型方案

陳穎源，李會艷，王若凡，王 江，王法光

CHEN Yingyuan1,LI Huiyan2,WANG Ruofan1,WANG Jiang1,WANG Faguang3

1.天津大學 電氣與自動化工程學院，天津300072

2.天津職業技術師范大學 自動化與電氣工程學院，天津300222

3.溫州市計量技術研究院，浙江 溫州325001

1.School of Electrical Engineering＆Automation,Tianjin University,Tianjin 300072,China

2.School of Automation＆ Electrical Engineering,Tianjin University of Technology＆ Education,Tianjin 300222,China

3.Wenzhou Institute of Measurement Technology,Wenzhou,Zhejiang 325001,China

1 引言

近年來，深度腦刺激（Deep Brain Stimulation，DBS）逐漸成為國際上主流的帕金森病療法之一[1-3]。DBS 療法能緩解帕金森病的運動癥狀，減少多巴胺類藥物用量，延緩藥物副作用的出現，具有可調節，可逆，刺激靈活等優點[1-5]。目前臨床上DBS 主要采用高頻周期脈沖刺激方案，刺激參數一般為頻率100～250 Hz，波寬200～400 μs。但是，由于帕金森病的發病機制和DBS 治療帕金森病的機制并不明確，如何選擇DBS 最優波形參數就變成了DBS應用的主要問題[4-5]。這里的最優指的是兩個方面，第一，如何設置參數能讓治療效果最好；第二，如何在保證治療效果的基礎上使刺激能量達到最小[6-7]。

最近研究發現非傳統DBS可能對帕金森病治療有更好的效果。Foutz 等人發現采用周期等腰三角波和傳統方波刺激效果相當，消耗能量減少[8]。Wongsarnpigoon等人研究了四種不同的刺激波形對哺乳動物軸突興奮性的作用機制[9]。Feng 等人則運用遺傳算法搜索非周期DBS 的參數[6-7]。相比傳統的高頻周期性脈沖，非傳統DBS 可能帶來的好處有：（1）降低了能量消耗，間接延長了電池壽命以及降低了手術風險；（2）由于刺激能量降低，刺激器對發病腦區周邊區域的溢出性刺激減少，副作用降低；（3）非傳統DBS 可能會避免周期性刺激帶來的抗藥性問題；（4）非傳統DBS 可能會對一些周期性刺激無效的病人有效。基于這些研究，本文借用電機控制中的脈寬調制（Pulse Width Modulation，PWM）思想[10]，產生一系列類似PWM 的DBS 脈沖信號，探索新的DBS 刺激波形。

DBS 的波形越復雜，描述DBS 波形的參數就越多。非周期性DBS 的描述參數往往多達幾十個，而最優參數的設定時間隨參數個數成指數增加。Feng 等人利用遺傳算法優化DBS 刺激參數，縮短了刺激器調節的時間[6-7]，但還是會消耗大量的時間和資源，因此最好的辦法還是可以減少設置參數。本文研究發現類PWM DBS 可以將涉及能量消耗的參數減小到一個，可以大大縮短優化進程。

由于倫理要求和實驗條件限制，目前對新型DBS的作用效果研究主要通過計算模型來進行。通過神經元模型進行調整和驗證然后再進行實驗研究，有利于降低實驗成本，保障動物福利。因此，能復現帕金森病放電節律的神經元模型DBS 波形研究非常重要。本文采用Terman 等人提出的帕金森病網絡模型[11-12]，該模型能夠模擬帕金森病主要發病腦區（基底核和丘腦）的放電節律。因此利用此模型研究DBS 波形參數對于動物實驗和實際應用具有現實的指導意義。

2 模型和方法

2.1 帕金森病網絡模型

帕金森病的網絡模型包含了四類神經元：丘腦底核（STN）神經元，蒼白球外側（GPe）神經元，蒼白球內側（GPi）神經元。和丘腦（TC）中繼神經元。根據文獻[11-12]的描述，其膜電位可由以下微分方程組描述：

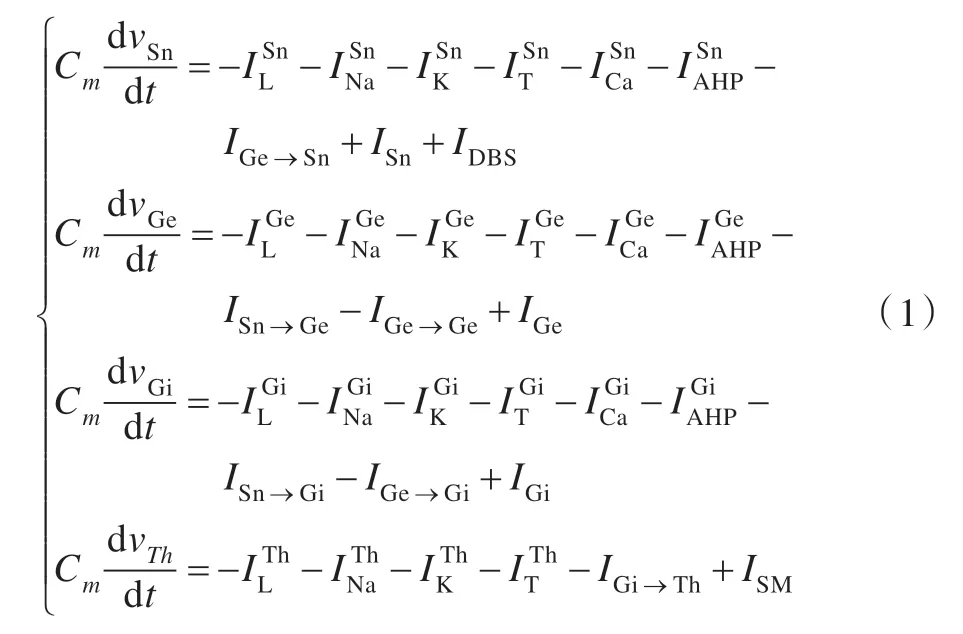
該模型為HH[13]類模型，模型中Cm為膜電容，vSn，vGe，vGi，vGi分別為STN，GPe，GPi 和TC 神經元的膜電位，ISn，IGe和IGi分別為相應神經元外加的輸入電流，在實際的神經元中可以看成是來自于紋狀體的投射電流。IL、INa、IK、IT、ICa和IAHP分別為相應神經元的漏電流，鈉電流，鉀電流，高閾值鈣電流，鈣電流和后超極化電流。仿真過程中具體參數設置可參考文獻[12，14-15]，本文不再贅述。

ISM為皮層感覺運動區對丘腦的興奮性電流輸入，其表現為周期的或間歇隨機的。皮層感覺運動區信號主要通過周期性脈沖模擬：

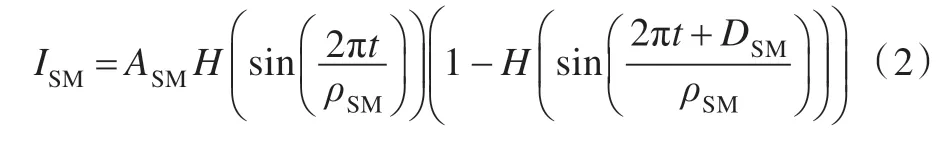
其中，ASM為方波信號的幅值，ρSM為方波信號的周期，DSM為每周期內方波信號的持續時間。

DBS 在STN 處加入，傳統的DBS 采用高頻周期脈沖的形式，表示如下：

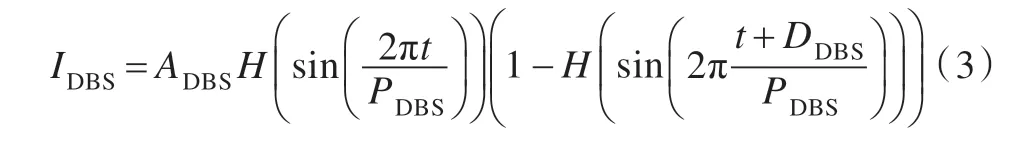
其中ADBS為DBS 的幅值，PDBS為DBS 的周期，DDBS為每個刺激周期內刺激的持續時間。H(x)為階躍函數。當x＞0 時，H(x)=1；當x＜0 時，H(x)=0。

一般來說，從α到β的突觸電流可以用下式表示：

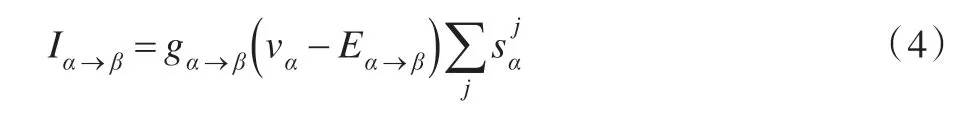
其中，α表示突觸前神經元，β表示突觸后神經元。在本文中，α和β取為GPe，GPi，STN 和TC。Eα→β為突觸反電勢，gα→β＞0 為最大突觸電導。突觸變量可用一階微分方程表示如下：

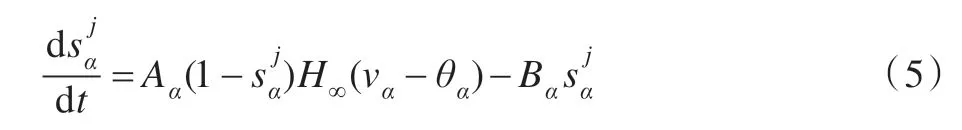
其中H∞(v)是近似的階躍函數。Aα和Bα是α神經元的突觸控制變量。神經元具體的連接形式采用Terman提出的稀疏網絡結構（圖1）[15]。每個GPe 神經元抑制其相鄰的兩個GPe 神經元，并且抑制兩個STN 神經元，兩個受抑制的STN 神經元之間間隔了三個STN 神經元。STN 神經元興奮其最近的GPe 神經元。STN 神經元之間沒有網絡連接。GPi神經元同時接受離其最近的GPe神經元的抑制性輸入和STN 神經元的興奮性輸入。GPi神經元內部也沒有連接。8 個GPi神經元分成兩組，分別對兩個TC 神經元傳出抑制性電流。

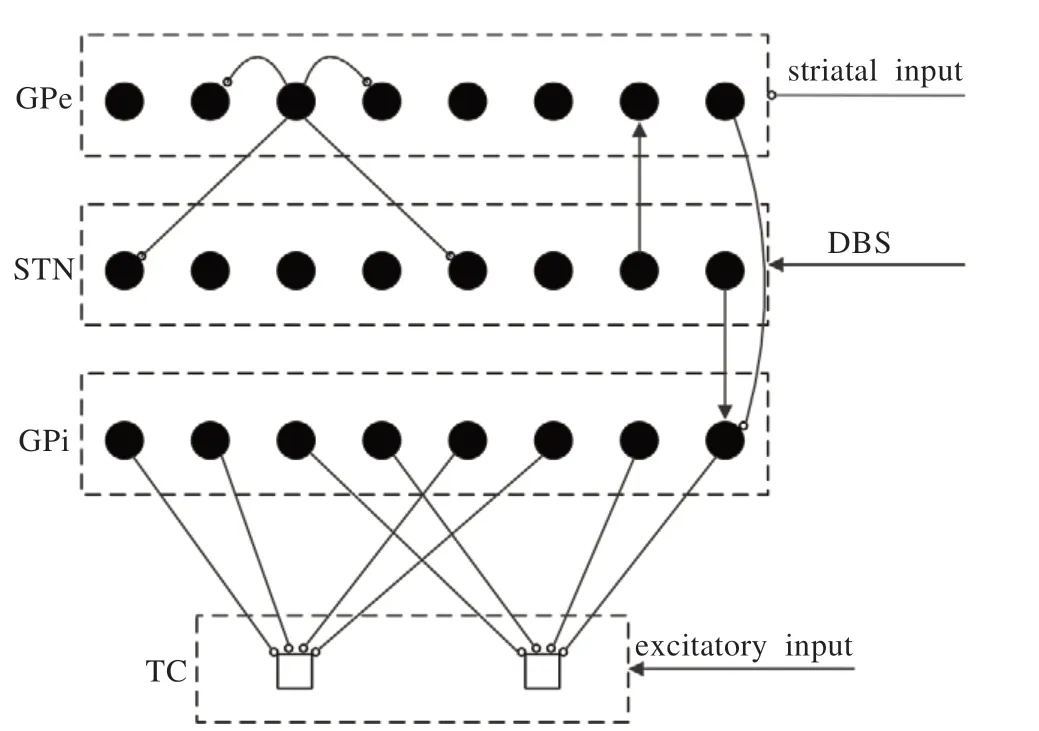
圖1 基底核及丘腦的稀疏網絡連接結構

2.2 丘腦中繼可靠性

圖2 為典型的帕金森狀態下丘腦中繼神經元的放電模式。圖2 底部畫出了皮層感覺運動區對丘腦的輸入，用周期性脈沖表示。

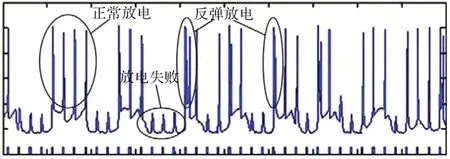
圖2 帕金森狀態下丘腦神經元的放電特征

（1）正常放電，一個皮層感覺運動區的輸入脈沖對應一個放電。

（2）放電失敗，輸入脈沖下無放電。

（3）反彈放電，一個輸入脈沖對應兩個或兩個以上放電（簇放電）。

在正常狀態下，丘腦能夠準確響應皮層感覺運動區的輸入。而在帕金森狀態下，正常放電減少，失敗放電和反彈放電增加，丘腦對皮層感覺運動區信號的中繼能力下降。因此，TC 細胞響應皮層感覺運動信號的中繼可靠性可以通過正常放電個數與皮層感覺運動區輸入脈沖個數的比值來表示[12，14-15]：

在正常狀態時，可靠性接近100%。而在圖2 中，由于反彈放電和放電失敗的存在，放電的可靠性下降。當可靠性下降到一定程度時，就認為出現了帕金森狀態的特征。因此，DBS 的目標就是要減少或消除放電失敗和反彈放電[3，6-7，12，14-15]。

2.3 基于PWM 思想的DBS 調制方法

PWM 是對脈沖寬度進行調制的技術，它通過對一系列脈沖的寬度進行調制，來等效地獲得所需要的波形（含形狀和幅值）。PWM 技術的理論基礎在于PWM 的面積等效原理[10]，即沖量相等而形狀不同的窄脈沖加在具有慣性的環節上時，其效果基本相同。這里沖量是指窄脈沖的面積，所謂的效果基本相同是指環節的輸出響應波形基本相同。由于PWM 波形生成比較簡單，可以生成不同脈寬的刺激信號。本文利用了PWM 的面積等效原理，在正弦波的正半周生成與正弦波等效的等幅不等寬的方波脈沖（SPWM 波），并以此作為DBS 刺激加入到帕金森網絡中，以改善DBS 的治療效果。

具體產生方法如圖3 所示。圖中SPWM 的載波為幅值A2，周期P2的等腰三角波，調制波為幅值A1，周期P1的正弦波，且載波的頻率比調制波高得多（即P1＜P2）。在調制波的正半周，當載波的幅值小于調制波的幅值時，SPWM 波輸出高位信號Ud，當載波的幅值大于調制波的幅值時，SPWM 波輸出為0，這樣就在正弦調制波的半個周期內呈兩邊窄中間寬的一系列等幅不等寬的矩形波（圖3）。在該設置下，SPWM 輸出的等效正弦基波幅值Uo可由下式近似計算：

在本文中為計算方便取Ud=A2，則由式（7）可得：

因此調整調制波和載波的參數就可以獲得期望的輸出SPWM 波。

根據面積等效原理，SPWM 波和正弦半波等效，那么SPWM DBS 消耗的能量就和正弦波的面積有關。如果用單位時間內的平均電流作為能量指標，則SPWM DBS 的平均電流可通過下式計算：

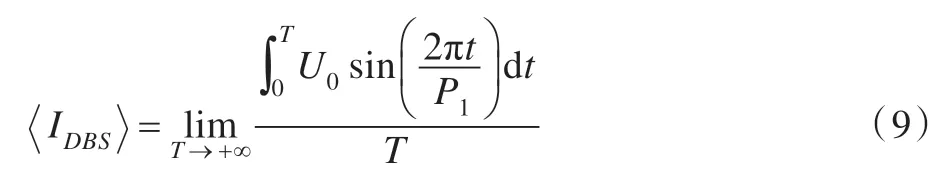
式中T為DBS的刺激時間，令T=NP1+ΔT，N為正整數，表示在整個刺激時間內包含的正弦調制波周期數；ΔT為不完整周期的正弦波刺激時間。由于DBS只取正弦正半周的波形作為調制波，當t∈[nP1，(n+0.5)P1](n=0,1,…，∞)時，由式（8）可得U0=A1，當t∈[(n+0.5)P1，(n+1)P1]時，U0=0。式（9）可變為：

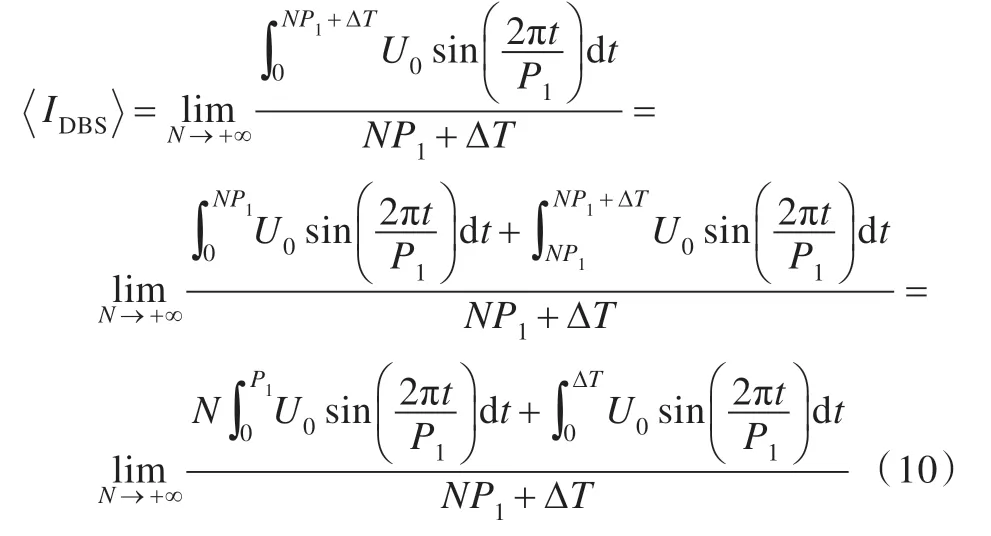
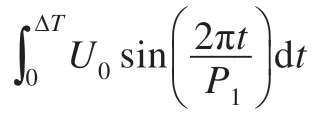
SPWM DBS 消耗的能量就由其正弦調制波的幅值A1唯一確定。這樣就把能量優化計算簡化到只有一個參數。

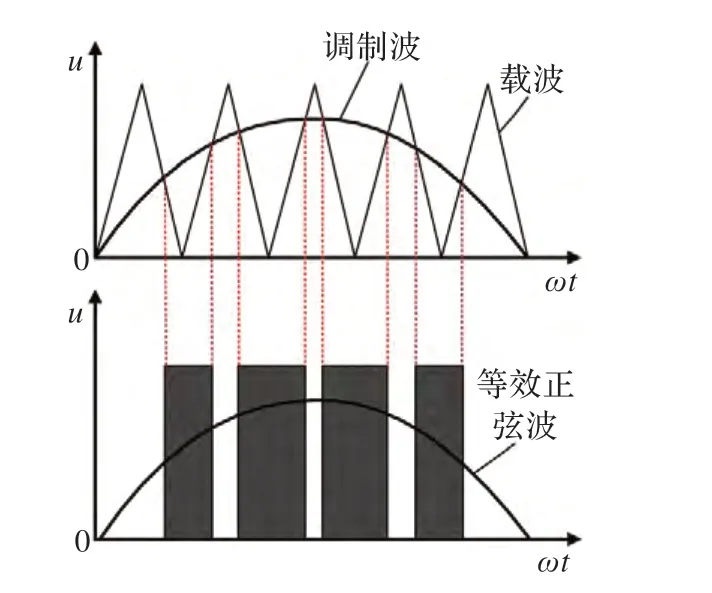
圖3 單極性SPWM 控制方式波形

3 仿真結果

利用PWM 技術在正弦調制波的正半周生成SPWM DBS 波形并加在帕金森病網絡模型上，考察其作用效果。仿真時間設置為4 s。根據波形參數的不同，可分為以下幾種情況進行討論：

（1）首先取國際上DBS 研究論文中常用的周期性脈沖DBS參數[3，6-7，12]ADBS=200 pA，DDBS=0.6 ms，ρDBS=6 ms，其平均電流為〈IDBS〉=20（pA/μm2）。然后取一組與該周期性脈沖DBS 能量等效的SPWM DBS，依據式（11）計算可得A1=20π ≈62.82(pA/μm2)。為仿真方便余下參數選為P1=12，A2=200，P2=2。圖4 為該SPWM DBS的作用效應，這里只畫出其中1 s的放電。該組SPWM DBS 與其能量等效的周期性脈沖DBS（ADBS=200 pA，DDBS=0.6 ms，ρDBS=6 ms）作用效果相同[3，12]。圖5 為SPWM DBS 和周期性脈沖DBS 的波形比較，可以發現由于正弦負半波的刺激設置為零，SPWM DBS 的波形比周期性DBS 更加集中，呈簇狀排列。

（2）在以上SPWM DBS 的基礎上減小DBS 的能量。根據式（9）令A1=20，P1=12，A2=200，P2=2，此時A1大約為上一種情況的三分之一，平均電流（能量）也減少為原來的三分之一。由圖6（a）可以發現TC神經元的可靠性較高。繼續減小A1時（A1=10，圖6（b）），TC 中繼神經元出現放電失敗和反彈放電，響應能力開始降低。

圖6（c），（d）分別為與圖6（a），（b）能量等效的周期性脈沖DBS 刺激方案。該方案在參數ADBS=200 pA，DDBS=0.6 ms，ρDBS=6 ms 的基礎上降低了占空比，分別取DDBS=0.2 ms 和DDBS=0.1 ms。其中DDBS=0.2 ms與A1=20 的SPWM DBS 等效，DDBS=0.1 ms 與A1=10的SPWM DBS 等效。當DDBS=0.2 ms 時TC 中繼神經元的可靠性良好，但當DDBS=0.1 ms 時TC 中繼神經元的可靠性下降。這說明SPWM DBS 和與其等效的周期性脈沖DBS 的作用效果是一致的。圖7 為圖6 對應的DBS 波形，可以發現SPWM DBS 的脈沖數比周期性DBS 多，但是其脈沖寬度，出現時間都和周期性脈沖不一致。這種不一致有利于降低神經元對刺激的適應性，因此也可能有利于降低周期性刺激帶來的抗藥性。

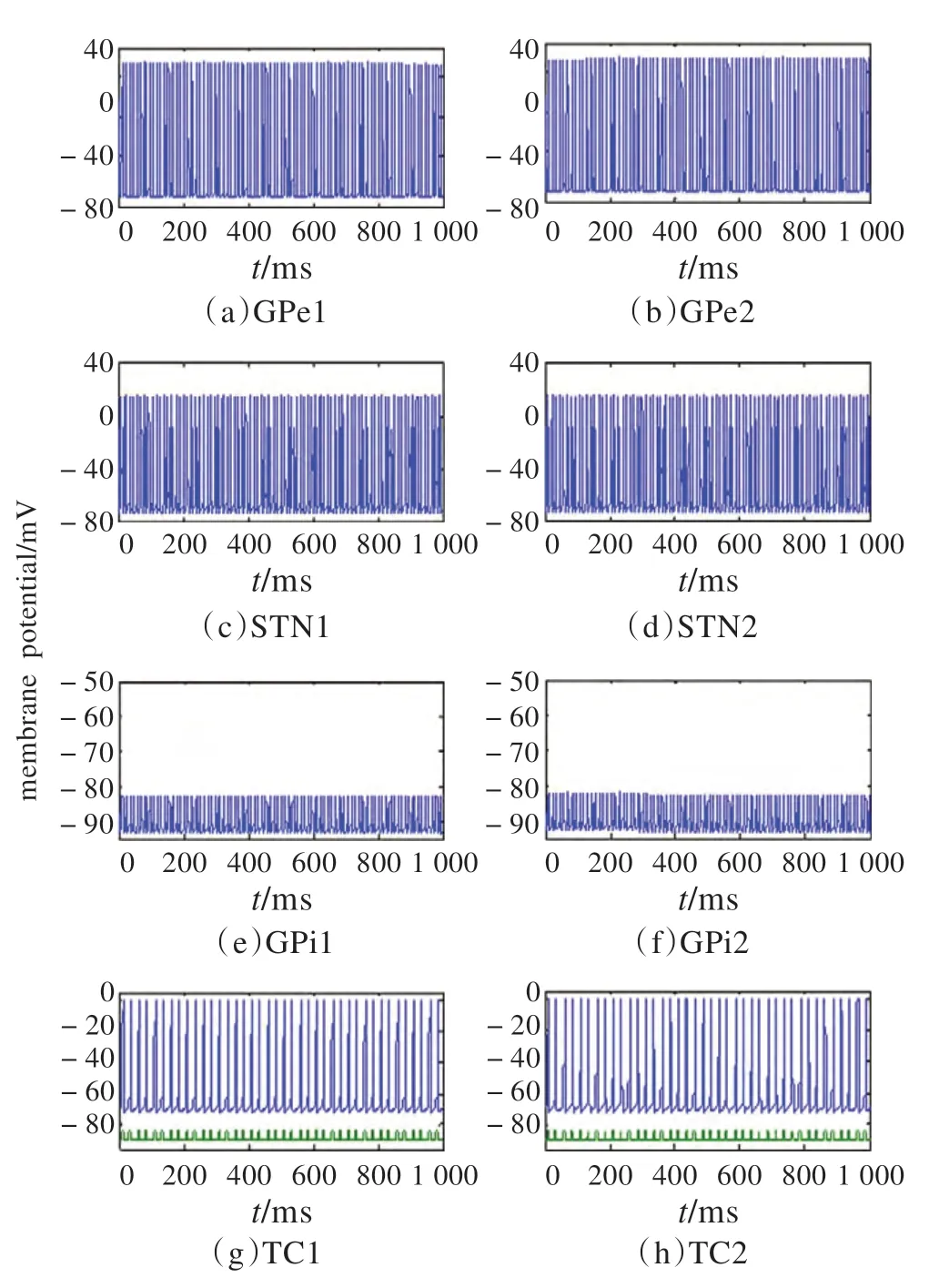
圖4 帕金森神經網絡在SPWM DBS 刺激下的效應，參數選取為A1=62，P1=12，A2=200，P2=2

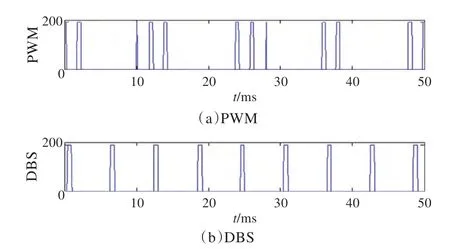
圖5 SPWM DBS 及其等效的周期性脈沖DBS 波形

（3）同時變化調制波幅值A1和載波幅值A2，在A1=20，P1=12，A2=30，P2=2 時帕金森病神經元網絡活動如圖8 所示。此時GPi 神經元完全被抑制（圖8（e）），其對TC 細胞的抑制性輸出幾乎為0（圖8（i）），TC神經元中繼能力良好（圖8（g））。在此基礎上減小A1(A1=10)，從圖8 右邊幾幅子圖可以發現，STN，GPe 和GPi 呈現簇放電狀態，GPi 輸出呈現相位震蕩狀態。這些明顯的帕金森病態特性破壞了TC 神經元的中繼能力。A1=10，P1=12，A2=30，P2=2 這組參數形成的PWM DBS 并不能使TC 神經元的中繼能力恢復正常。

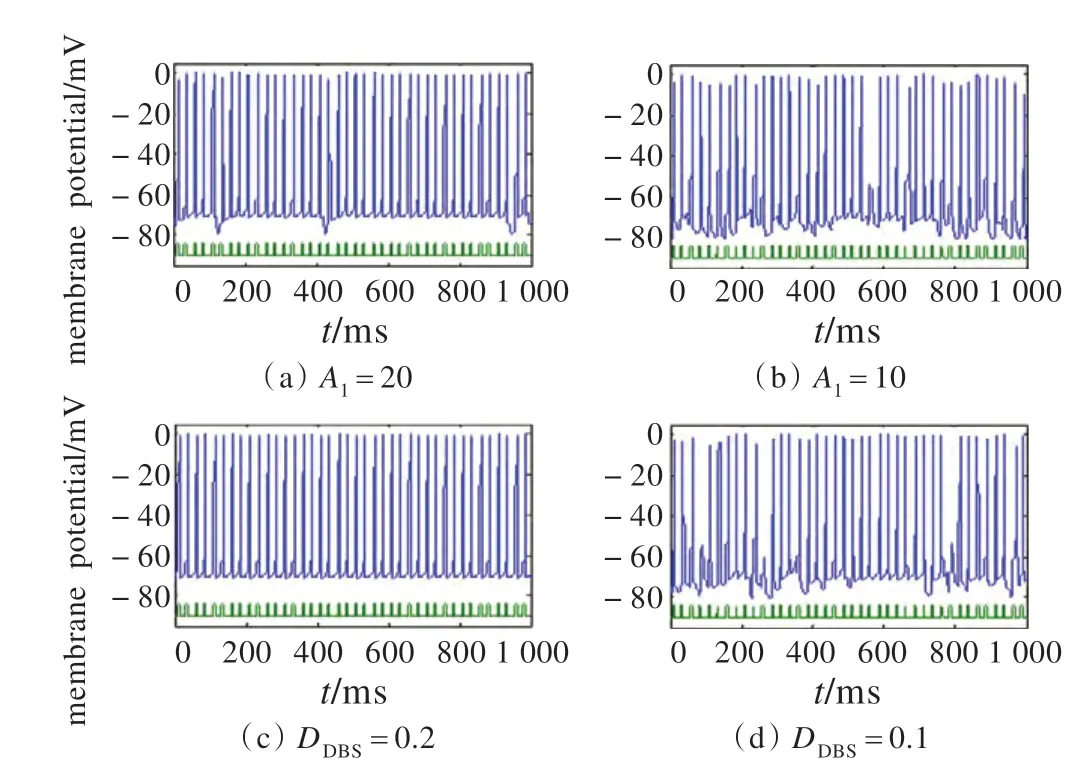
圖6 SPWM DBS 與在普通的周期性脈沖DBS 刺激效應比較，參數選取為P1=12，A2=200，P2=2

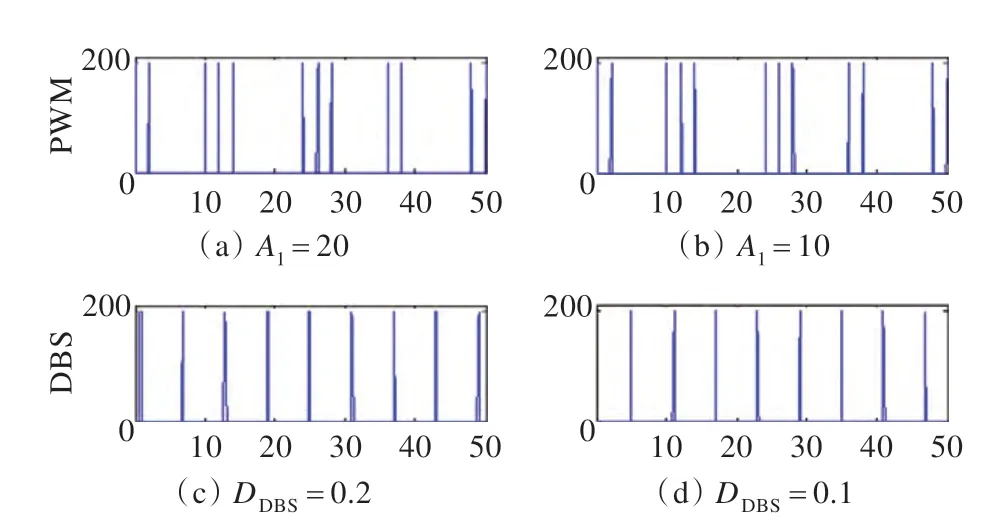
圖7 SPWM DBS 波形及其等效的周期性DBS 波形比較

通過以上研究可以發現，在本文的參數設置下，SPWM DBS 的作用效應與與其能量等效的周期性脈沖DBS 對帕金森病神經元網絡的作用效應是一致的。在影響SPWM DBS 的四個參數中，調制波幅值A1對帕金森病神經元網絡的影響最大。這不僅是由于A1的變化使得SPWM DBS 的波形產生了變化，更重要的是A1決定了SPWM DBS 的輸出能量。因為由式（11）可知，不管其他參數怎么變化，影響SPWM DBS 波形能量的參數只有一個，那就是A1。在仿真中也發現，A1減小到一定程度時，會使TC 神經元中繼能力減弱，其他參數也會對帕金森病神經元網絡的放電模式產生影響，但是作用不如A1，這說明DBS 刺激效果和刺激能量之間關系密切。因此，A1是影響SPWM DBS 效應的關鍵參數。這種設置的另一個好處就是為DBS 的能量優化提供了方便。在優化能量的時候，只需要在保證效果的前提下，盡量減小A1就可以了。這大大簡化了優化時的計算量。

圖8 帕金森神經網絡在PWM 波刺激下的效應，參數選取為(a，c，e，g，i) A1=20，P1=12，A2=30，P2=2；（b，d，f，h，j）A1=10，P1=12，A2=30，P2=2

4 結束語

本文針對當前DBS 波形參數設置困難等問題，提出基于PWM 思想調制DBS 波形的方案，并通過帕金森網絡模型對SPWM DBS 的作用效果進行了驗證，發現SPWM DBS 和傳統的周期性脈沖DBS 作用效果一致。和傳統的周期性脈沖DBS 相比，本文提出的SPWM DBS 屬于一種新的刺激方式，它具有以下優點：（1）相對于周期性DBS，SPWM DBS 的波形變化豐富，有利于降低神經元適應性對網絡放電的影響，從而可能會減少由于周期性方波持續刺激造成的抗藥性等問題；（2）SPWM DBS 的波形和傳統的DBS 波形相區別，可能令對周期性DBS 無效的病人受益；（3）SPWM DBS 減少了刺激能量涉及的參數個數，為能量優化提供了方便。本文的研究為DBS 的參數設置提供了一種新的規則，也為臨床上開發新型DBS 提供了參考。最后必須指出的是，由于DBS 輸出主要為脈沖形式，PWM 技術為調制DBS脈沖提供了有效工具，本文僅提出了基于PWM 調制DBS 的思想并對SPWM DBS 的參數設置做了初步研究，在以后的工作中還需要詳細研究不同調制方法產生的DBS 對帕金森病神經元網絡的作用效應問題。

[1] 陳生弟.帕金森病[M].北京：人民衛生出版社，2006.

[2] 張元鵬，李新鋼.腦深部刺激治療帕金森病的研究進展[J].醫學綜述，2005，11（4）：356-358.

[3] Schiff S J.Towards model-based control of Parkinson’s disease[J].Philosophical Transactions of the Royal Society a-Mathematical Physical and Engineering Sciences，2010，368（1918）：2269-2308.

[4] Benabid A L.Deep brain stimulation for Parkinson’s disease[J].CurrOpinNeurobiol，2003，13（6）：696-706.

[5] Perlmutter J S，Mink J W.Deep brain stimulation[J].Annual Review of Neuroscience，2006，29：229-257.

[6] Feng X J，Greenwald B，Rabitz H，et al.Toward closed-loop optimization of deep brain stimulation for Parkinson’s disease：concepts and lessons from a computational model[J].Journal of Neural Engineering，2007，4（2）：14-21.

[7] Feng X J，Shea-Brown E，Greenwald B，et al.Optimal deep brain stimulation of the subthalamic nucleus-a computational study[J].Journal of Computational Neuroscience，2007，23（3）：265-282.

[8] Foutz T J，McIntyre C C.Evaluation of novel stimulus waveforms for deep brainstimulation[J].Journal of Neural Engineering，2010，7（6）.

[9] Wongsarnpigoon A，Grill W M.Energy-efficient waveform shapes for neural stimulation revealed with a genetic algorithm[J].Journal of Neural Engineering，2010，7（4）.

[10] 王兆安，黃俊.電力電子技術[M].4 版.北京：機械工業出版社，2001.

[11] McIntyre C C，Grill W M，Sherman D L，et al.Cellular effects of deep brain stimulation：Model-based analysis of activation and inhibition[J].Journal of Neurophysiology，2004，91（4）：1457-1469.

[12] Rubin J E，Terman D.High frequency stimulation of the subthalamic nucleus eliminates pathological thalamic rhythmicity in a computational model[J].Journal of Computational Neuroscience，2004，16（3）：211-235.

[13] Hodgkin A L，Huxley A F.A quantitative description of membrane current and its application to conduction and excitation in nerve[J].Journal of Physiology，1952，117（4）：500-544.

[14] 陳穎源.基于模型的帕金森病分析與控制[D].天津：天津大學，2011.

[15] Terman D，Rubin J E，Yew A C，et al.Activity patterns in a model for the subthalamopallidal network of the basal ganglia[J].Journal of Neuroscience，2002，22（7）：2963-2976.