基于內插外推的隨機頻率步進信號旁瓣抑制

劉俊豪， 付朝偉

（上海無線電設備研究所，上海200090）

0 引言

頻率步進（Stepped Frequency，SF）信號具有瞬時窄帶和合成寬帶的優點，因此在高分辨雷達 中 廣 泛 應 用［1］。隨 機 頻 率 步 進（Random Stepped Frequency，RSF）信號兼具頻率步進信號優點的同時［2］，具有理想的“圖釘形”模糊函數，且具有優良的低截獲概率、電磁兼容性以及抗射頻干擾等特性。同時，RSF 信號易于工程實現，能與普通雷達信號體制兼容［3］，已受到雷達領域的廣泛關注。

但是，RSF信號的隨機性導致合成高分辨距離（High Resolution Range，HRR）圖像具有較高的隨機調制噪聲。同時，在有些應用中，如頻帶斷續［4-6］、阻塞式干擾或波形周期受限的寬帶信號等情況［7］，由于其頻帶不連續的影響，導致距離旁瓣電平進一步抬高，容易引起弱目標淹沒在強目標旁瓣中，或多目標旁瓣疊加形成虛假目標等現象。

目前，對于RSF信號的旁瓣抑制，文獻［5，6］從信號設計的角度，通過跳頻編碼的設計抑制匹配濾波后的旁瓣，但在頻帶缺失時該方法的旁瓣抑制性能有限。文獻［8，9］采用CLEAN 算法逐次去除強目標旁瓣對其他目標的影響，得到旁瓣抑制效果，但該方法適用于距離單元相互獨立的情況，因此在高分辨雷達應用中受到限制。文獻［10］通過設計失配濾波器實現距離旁瓣抑制，但存在SNR 損失，并且當處理窗邊緣處存在目標時，邊緣效應會嚴重影響處理窗內的旁瓣抑制效果。

內 插 外 推 法（Interpolation and Extrapolation，IE）由Sacchi和Ulrych等人提出，用于提高譜估計的精度［11］。

本文在IE算法原理的基礎上，由隨機跳頻編碼設計相關矩陣，利用柯西-高斯模型先驗信息的貝葉斯準則進行最大后驗（Maximum a Posterior，MAP）概率函數的最小化，從而得到具有內插外推的高分辨離散傅里葉變換（Discrete Fourier Transform，DFT）矩陣，并通過迭代算法實現，最后仿真分析驗證了其旁瓣抑制性能和參數估計精度。

1 信號模型

假設RSF信號一個波形周期由M 個脈沖組成，每個脈沖的步進量從頻率集｛0，Δf，…，（N-1）Δf｝（N ＞M）中隨機抽取，即第m（m ＝0，1，…，M-1）個脈沖頻率為Fm＝fc+fm，其中fc為載頻，fm＝cmΔf，cm∈｛0，1，…，N-1｝為頻率跳變編碼，則一個波形周期發射信號可以表示為

式中：Tp為脈沖寬度；Tr為脈沖重復間隔（Pulse Repetition Interval，PRI）；rect（·）為 矩 形 窗函數。

由于fm隨機變化，如圖1所示，因此RSF信號具有良好的低截獲概率和抗射頻干擾特性。

圖1 RSF信號頻率步進示意圖

設原始距離分辨單元（即脈寬Tp對應的距離）內有K 個目標，則對RSF回波信號在每個子脈沖上進行一次采樣，得到對目標距離像的頻域非均勻采樣，其中第m 個采樣點表示為

式中：c為光速；Rk和γk分別對應第k 個目標的距離和幅度。

因此，一個波形周期采樣序列向量可表示為

一個波形周期采樣序列匹配接收后的合成距離像記為x∈CN×1，其中CN×1為N×1維的復數集合，并受到方差為σ的高斯白噪聲n的影響，即n～N（0，σIM），其中IM為M 維單位矩陣，則該過程表示為

式中：相關DFT 矩陣A ∈CM×N表示為

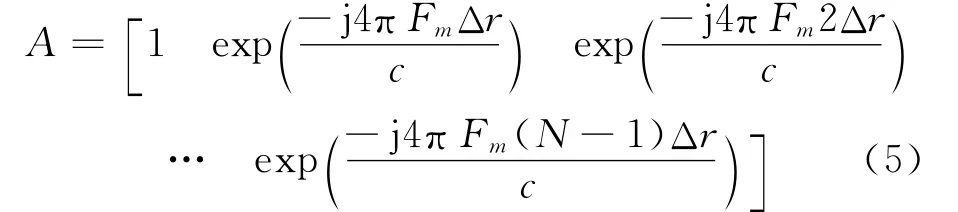
式中：Δr為距離分辨率

其中：

對于式（4），需要從采樣序列s中恢復出距離像x，其最小二乘解為

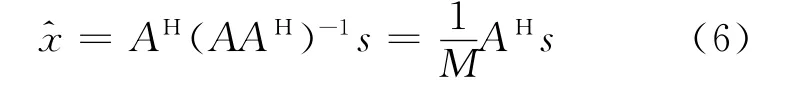
式中：（·）H表示共軛轉置。

式（6）又稱為相關處理（Coherent Process-ing，CP）方法，由于頻域采樣序列s頻點缺失，因此恢復出的距離像旁瓣較高。

同時，由于DFT 矩陣A 的秩rand（A）＝M ＜N，因此不能得到穩定的解。

下面通過貝葉斯準則，利用距離像的頻譜特性等先驗信息，對缺失的頻點通過內插外推的迭代過程得到高分辨距離像。

2 內插外推算法原理

對于式（4）表示的線性欠定方程，存在多個解，為求取其唯一解，構造正則化目標函數為

式中：正則化矩陣Φ（x）對解的特征進行約束；‖·‖2表示2范數。

對于n～CN（0，σ2nIM）的復高斯白噪聲，采樣序列的條件概率密度分布函數為

如果x 的先驗概率密度函數與參量σx有關，即表示為p（x｜σx），則似然函數表示為

因此，對于給定的σx和σn，當p（x｜s，σx，σn）最大時，得到MAP的估計值。

假設復變量xn服從柯西分布，即表示為

式中：σx為尺度參數。

因此，柯西分布的正則化矩陣Φ（x）為

故正則化目標函數式（7）可表示為

式（12）的解為

式中：λ＝σ2n／σ2x；Q ∈CN×N為對角矩陣，對角線上元素為

3 IE算法實現過程

式（13）表示的解與最小二乘解類似，但是對角矩陣Q 是非線性的，并且與xn有關，因此需要構造一種迭代的方法來求解x。

利用恒等式

得到式（13）表示的最優解還可表示為

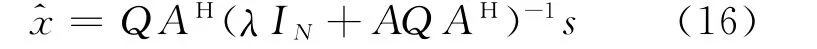
令b＝（λIN+AQ AH）-1s，迭代過程數學形式為

因此，根據式（17）～式（18）得到內插外推法的迭代過程。

步驟1：

a）根據距離分辨率、距離范圍等參數構造相關矩陣A；

b）初始化x（0）＝AHs，其中x（0）即為匹配接收結果；

c）由初始解x（0）得到矩陣Q（0）；帶入式（17）和式（18）得到x（1），此時k＝1。

步驟2：由解x（k）得到矩陣Q（k）；k＝k+1；由式（17）～式（18）得到x（k+1）。

步驟3：判斷迭代終止，如果滿足式（19）則終止迭代，否則轉到步驟2。

式中：ε為接近于0的常數。一般迭代次數在10次以內即可滿足要求。

4 仿真與分析

仿真參數設置：

a）載頻fc＝10GHz；

b）脈沖寬度Tp＝0.1μs；

c）脈沖重復間隔Tr＝2μs；

d）最小頻率步進量Δf＝5 MHz；

e）可用頻點數N＝512；

f）頻率編碼在0～511 內隨機抽取M ＝64點，并且仿真過程中加入SNR 為20dB的高斯白噪聲。

RSF信號合成成像過程中，通過少的頻點合成全頻帶對應的高分辨距離像。為了驗證本文IE算法對旁瓣的抑制性能，仿真過程中目標參數設置分兩種情況：

一是檢測窗內單個目標，距離為100m 且目標幅度為1；

二是檢測窗內存在多個強弱目標，且其距離分別為100，101，102，110，115 m，目標幅度分別為1，1，0.3，0.3，1。

常規相關處理（CP）方法和本文IE 旁瓣抑制算法仿真結果，如圖2所示。其中，當處理窗內只有一個目標時，如圖2（a）所示，CP結果存在較高旁瓣基底，且主旁瓣電平（Peak Sidelobe Level，PSL）為10dB；而IE處理對缺失的頻點進行內插外推并進行距離合成，其主旁瓣比明顯提高，圖中可以看出進行旁瓣抑制的IE 算法比CP 方法的旁瓣電平降低近30dB。

圖2 基于IE的RSF信號旁瓣抑制仿真結果

當檢測窗內存在多個目標時，CP處理結果和IE旁瓣抑制結果如圖2（b）所示，由于多個目標的共同作用，導致相關處理結果旁瓣電平提高，此時強目標的PSL為5dB，使得弱目標在CP處理后較難識別。

IE處理結果雖然旁瓣電平有所提高，但旁瓣電平在-30dB附近，5個目標在處理窗內能夠清晰辨別。

對于單目標情況，加入不同SNR 的高斯白噪聲，進行200次Monte-Carlo實驗得到相關處理方法和IE旁瓣抑制方法距離像恢復重建的均方誤差曲線，如圖3 所示，圖中同時給出了不同SNR 對應的克拉美-羅下限（Cramer-Rao Lower Bound，CRLB）。

圖3 距離像重建的均方誤差曲線

圖中可以看出，IE 方法的估計精度遠優于CP方法，且IE 旁瓣抑制后的估計精度逼近CRLB且一致性較好。

5 總結

本文提出采用內插外推算法進行隨機頻率步進雷達信號旁瓣抑制，利用柯西-高斯模型的先驗信息得到具有內插外推性質的DFT 矩陣，從而得到RSF信號在缺失頻點情況下高分辨距離像的恢復。

理論分析和數值仿真表明，所采用的方法能夠進行有效的RSF信號距離旁瓣抑制，并且參數估計精度接近CRLB。

［1］ Donald R W.High Resolution Radar［M］.Nor-wood，MA：Artech House，1995.

［2］ Axelsson S R J.Analysis of Random Step Frequency Radar and Comparison With Experiments［J］.IEEE Transactions on Geoscience and Remote Sensing，2007，45（4）：890-904.

［3］ 彭歲陽，歐建平，盧大威，等.基于高重頻隨機頻率步進寬帶雷達的頻率匹配算法［J］.系統工程與電子技術，2011，33（4）：759-763.

［4］ 袁建華，劉興釗.非連續譜高頻雷達跳頻波的信號處理［J］.通信技術，2003，（8）：14-16.

［5］ 趙德華，毛智能，位寅生.全隨機跳頻脈沖信號設計與處理［J］.系統工程與電子技術，2014，36（3）：464-468.

［6］ 位寅生，劉永坦，許榮慶.準隨機跳頻信號的二維處理［J］.電子學報，2003，31（6）：801-804.

［7］ 馮永新，高瑜，潘成勝.寬帶均勻頻譜干擾對GPS接收機的影響分析［J］.計算機仿真，2008，25（1）：27-30.

［8］ Schwarz U.Mathematical-statistical Description of Iterative Beam Removing Technique （Method Clean）［J］.Astronomy & Astrophysics，1978，65（3）：345-356.

［9］ Bose R，Freedman A，Steinberg B D.Sequence Clean：A Modified Deconvolution Technique for Microwave Images of Contiguous Targets［J］.IEEE Transactions on Aerospace and Electronic Systems，2002，38（1）：89-97.

［10］ Xuehui H，Liangbing H，Zhaoping W，et al.Optimal Sidelobe Suppression Filters Design with a Constraint of Maximum Loss in Process Gain［C］.IET International Radar Conference，Guilin，China，2009.

［11］ Sacchi M D，Ulrych T J，Walker C J.Interpolation and Extrapolation Using a High-resolution Discrete Fourier Transform［J］.IEEE Transactions on Signal Processing，1998，46（1）：31-38.