分布式MIMO系統線形小區天線位置優化研究

付明浩，李岳衡

分布式MIMO系統線形小區天線位置優化研究

付明浩，李岳衡

對于研究分布式MIMO（Multiple-Input Multiple-Output）系統線形小區基站側天線端口的位置優化問題具有很重要的現實意義。以最大化小區平均遍歷容量為目標函數，研究了分布式MIMO系統中基站側天線位置的最優分布問題。根據仿真結果可得出如下結論：基于粒子群智能優化算法的次優搜索可以有效解決該類優化問題；對天線最優位置產生影響的主要因素包括：用戶位置的分布、基站天線的布局方式以及基站側天線端口的數目等。

分布式MIMO；粒子群算法；平均遍歷容量；天線位置優化

0 引言

現實生活中，無線通信系統的建模會綜合考慮到人們的生活需求和所處地理環境的影響，常見的系統模型有蜂窩狀的六邊形小區，也有圓形、三角形以及線形小區。當身處筆直的街道、河流、鐵路和高速公路時，移動終端近似可以看成只在直線范圍內活動，通常這類小區都被建模成線形小區。

考慮一個線形小區分布式MIMO系統，如圖1所示：

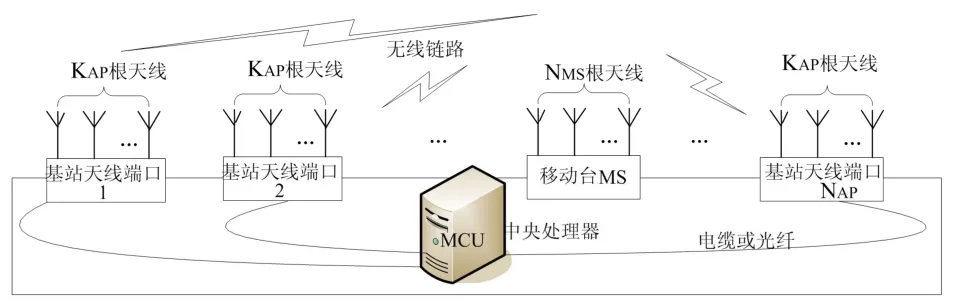
圖1 線形小區分布式MIMO系統(NAP,KAP,NMS)

NAP個天線端口AP分散放置在線形小區內，每個AP配置有KAP根天線，移動終端MS則配置有NMS根天線，記為系統。考慮下行通信鏈路，即AP側為信號發射端，MS側為信號接收端。

本文將著重研究分布式MIMO系統在線形小區中基站側天線端口位置的分布問題。在分布式MIMO系統中，基站側天線的位置分布直接影響著通信系統的各項性能[1]-[2]，不同的位置分布會對系統的平均誤比特率和平均遍歷容量等產生很大的影響[3]。生活中不乏線形小區的例子，比如繁華的街道、筆直的高速公路等都可以建模成線形結構的小區，因此，對于線形小區中基站側天線位置分布的研究具有很重要的現實意義。

1 系統模型

本文關于線形小區中天線位置分布的研究采用的系統模型可簡化如圖2所示：

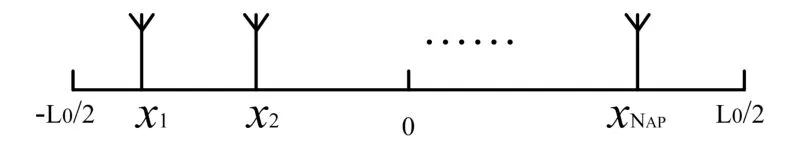
圖2 線形小區中天線位置分布示意圖

在長度為L0的線形小區中，假設小區中心處坐標為0，NAP個天線端口AP依次分布在線形小區中，位于小區中不同的地理位置處，為方便統計，假設第i(1≤i≤NAP)個 AP的坐標記為xi，并且有x1＜x2＜…＜xNAP；每個AP配置有KAP根天線；移動終端MS配置有NMS根天線，且在整個線形小區中均勻分布。

考慮如下建模，假設無線信號經歷的是復合衰落信道，即充分考慮了陰影效應、路徑損耗以及快衰落對無線信道的影響，其中快衰落采用了常見的Rayleigh衰落模型；考慮下行通信鏈路；發射天線采用等功率分配方案。

2 優化問題的提出

本文的研究內容是以最大化小區平均遍歷容量為目標函數來尋求天線位置的最優解[4]，該優化問題的數學模型如公式（1）：

式中，x1,x2,…,xNAP分別表示各個天線端口的位置，那么小區平均遍歷容量取得最大值時各個天線端口的位置p1,p2,…,pNAP即為該優化問題的解如公式（2）：

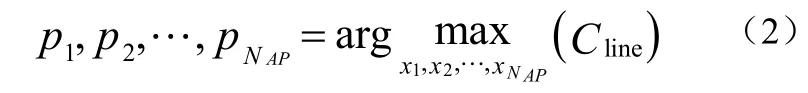
當用戶的位置u在線形小區中服從均勻分布時，其概率密度函數如公式（3）：

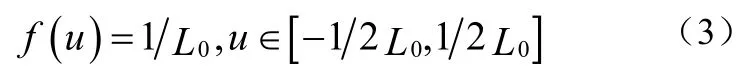
那么由下行鏈路遍歷容量的表達式式可知公式（4）：

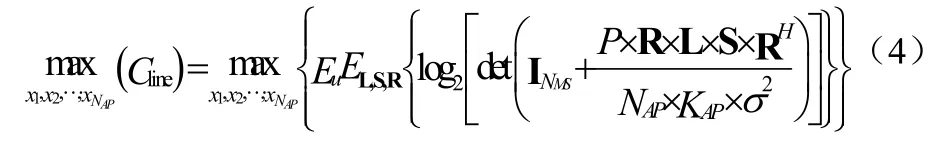
由矩陣的性質，可知公式（5）：

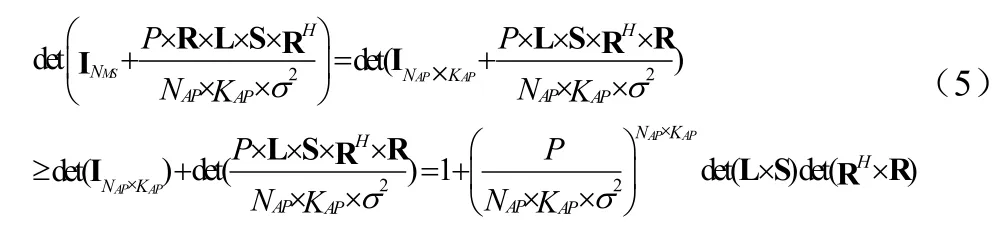
上式中，由于快衰落矩陣R以及陰影效應S均不是天線位置的函數，同時調換式(4)中Eu和EL，S，R的順序，那么得到公式（6）、（7）：

此時，該優化問題就轉化為求遍歷容量下界的最大值問題，注意此時求得的為次優位置，那么優化問題的解可以轉化為下式的求解得公式（8）：

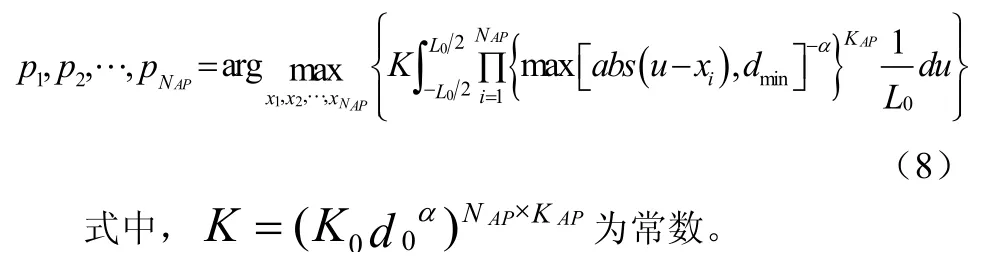
3 粒子群優化算法求解優化問題

用粒子群優化算法（PSO）求解小區中天線位置的分布問題時，基站側天線處于一維空間中，那么對應優化問題的搜索區域即為一維空間，此時，各個粒子的位置、速度以及個體最優解均可以用一個實數來表示，粒子的適應度即為天線端口分布于粒子所在位置時的小區平均遍歷容量Cline。根據PSO算法流程，得出求解該優化問題的步驟如下：

STEP1：初始化粒子群。假設搜索區域內粒子的個數為M，那么需要初始化M個粒子的位置信息、速度信息以及初始的個體最優解初始化迭代次數N=0；并設置迭代次數的門限值N0、學習因子c1和c2、慣性系數λ的值。此外，還需要設置粒子運動的速度上限vmax，限制粒子的速度在區間中，以免速度值過大，導致粒子陷入局部最優解。

STEP2：計算M個粒子的初始適應度。根據線形小區平均遍歷容量的表達式，結合各個粒子的位置信息，計算適應度Si，并找出適應度最大的粒子，作為初始的全局最優解Gbest0。

STEP3：更新粒子的位置和速度。假設上一次的迭代次數為k，那么第i(1≤i≤M)個粒子經過k+1次迭代之后的位置和速度可以按照下式進行更新為公式（9）：

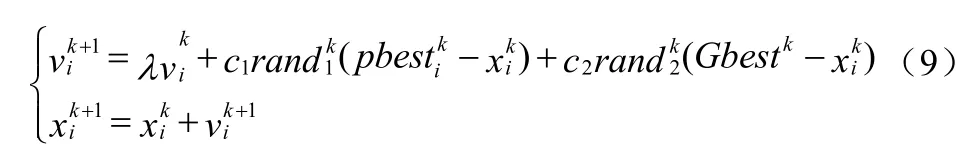
更新完速度和位置之后，需要判斷該粒子是否還在搜索區域內，若已經超出了該區域，那么需要重新更新粒子，重復STEP3。

STEP5：重復STEP3～STEP4，直到迭代次數k達到門限值N0，滿足算法的收斂準則，輸出全局最優解Gbest，即優化問題的次優解。

4 仿真與分析

本節主要利用粒子群優化算法求解線形小區中天線位置的最優分布問題[5]，并驗證該算法的有效性，同時通過各種場景的模擬，研究線形小區中天線位置對小區平均遍歷容量的影響以及系統中各參數對天線最優位置的影響，主要仿真參數，如表1所示：

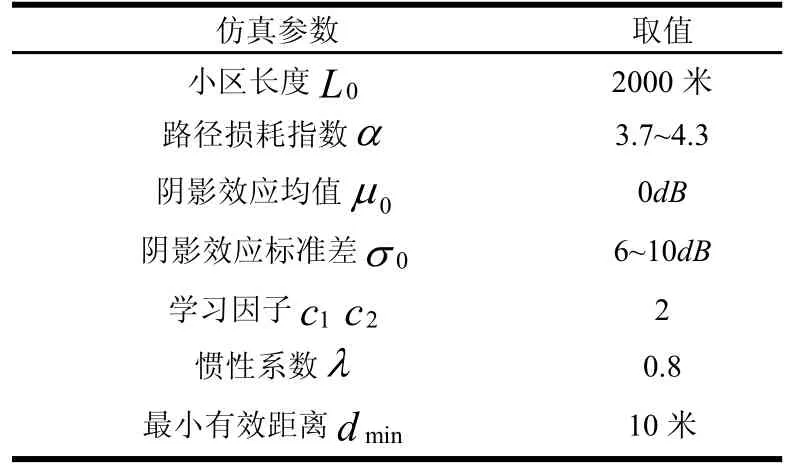
表1 線形小區仿真參數列表

用粒子群算法求解線形小區中AP位置的最優分布時，首先需要對粒子群體進行初始化。如圖3所示：

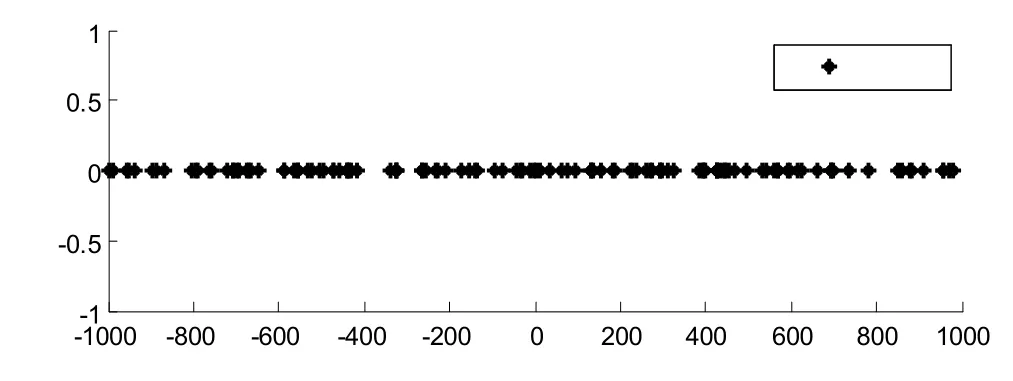
圖3 線形小區中粒子群體的初始位置

為一維搜索空間域中粒子群體的初始位置，粒子隨機分布在直線區間[-1000,1000]中。

在搜尋最優解的過程中，粒子的位置不斷的更新，經過一定次數的迭代后，粒子群體會收斂在最優解區域。如圖4所示：

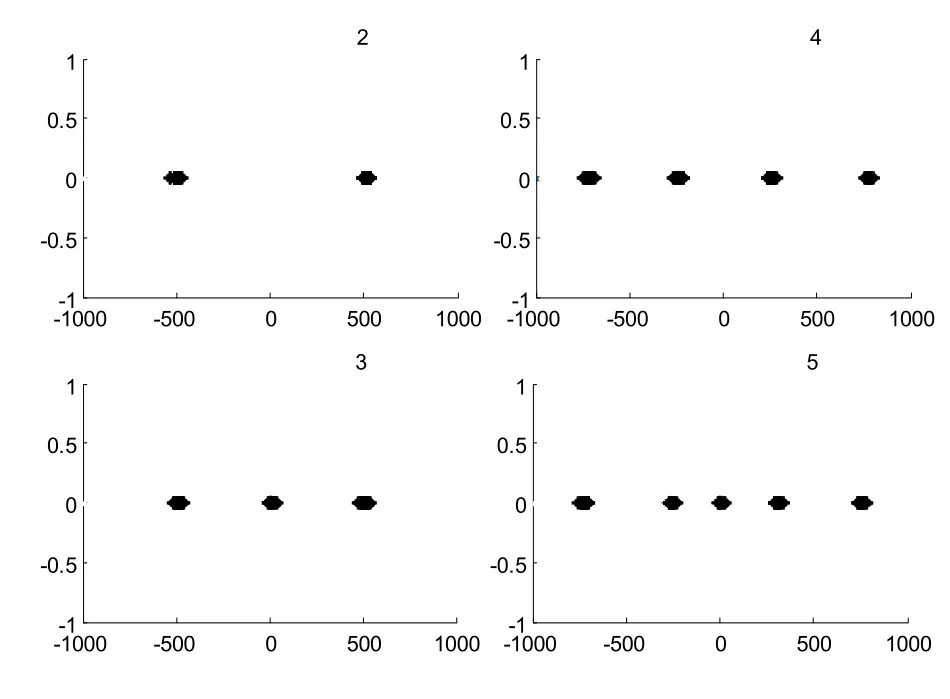
圖4 線形小區中基于粒子群算法的次優搜索

為線形小區中AP數目分別為2,3,4,5時對應優化問題的次優解，圖中粒子高度聚集的位置即為天線分布的最優解區域，全局最優解的位置即為粒子群搜索到的次優解，即天線的次優位置。從仿真結果可以看出，當AP數目為偶數時，所有的AP均分布在關于小區中心兩兩對稱的位置；若為奇數時，有一個AP放置在小區中心位置，其余AP均分布在關于小區中心兩兩對稱的位置。

仿真結果顯示了天線位置分布對線形小區平均遍歷容量的影響，充分說明了小區平均遍歷容量會隨著天線位置的變化而發生變化，進一步肯定了研究線形小區中天線位置分布的必要性如圖5所示：

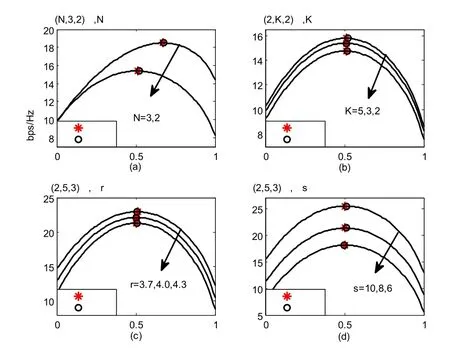
圖5 線形小區遍歷容量與天線位置的關系

圖5中，坐標原點（0,0）表示線形小區的中心位置，仿真中主要考慮了天線端口數目N分別為2和3兩種場景，當N=2時，兩個AP關于小區中心對稱放置；當N=3時，其中一個AP置于中心處，其余兩個AP關于小區中心對稱放置。圖中天線的最優位置是通過計算機搜索得到，次優位置由粒子群算法搜索得到，觀察發現，由粒子群算法得到的次優位置可以很好地逼近最優位置，能有效解決該優化問題。

其中，(a)圖展示了同一位置處，天線端口數目N對小區平均遍歷容量的影響，遍歷容量隨著N的增大而提高；同時從圖中可以看出，N為2時，小區平均遍歷容量大約在歸一化距離為0.5時達到最大；N為3，天線分布的最優位置開始向小區邊緣偏離。

(b)圖中，固定了天線端口數目和用戶端的天線數目，即研究了（2，K，2）系統中K對小區平均遍歷容量的影響，其中K表示每個天線端口安裝的天線數目，觀察小區平均遍歷容量的變化曲線可以發現，隨著K的增加，小區平均遍歷容量隨之而增加；同時，當K的取值不同時，天線分布的最優位置始終保持不變，其歸一化距離始終維持在0.5左右，這是因為K的取值并不影響基站天線與用戶天線的平均接入距離。關于用戶端天線數目對天線最優位置的影響與K值對系統性能的影響極其相似，為避免贅述，便沒有給出仿真結果。

(c)圖和(d)圖中，分別研究了（2,5,3）系統中，在不同信道參數下，天線位置對線形小區平均遍歷容量的影響。從(c)圖中可以看出，當天線端口處于同一位置時，小區平均遍歷容量隨著路徑衰落指數的增加而下降，這是因為，隨著路徑衰落指數的增加，系統中的路徑損耗逐漸增強，從而導致接收端信噪比的下降，那么根據香農定理，系統的遍歷容量也會隨之而降低。

觀察(d)圖可以發現，當天線端口固定于某一位置時，小區平均遍歷容量會隨著陰影效應標準差的增加而提高，與(b)圖類似，當各信道參數取值不同時，天線分布的最優位置大致保持不變，從一定程度上說明了信道參數并不是影響基站側天線端口位置最優分布的主要因素。

5 總結

本文主要基于粒子群智能優化算法研究了線形小區中基站側天線位置的最優分布問題。為此首先介紹了線形小區的系統模型，在此基礎上，以最大化小區平均遍歷容量為目標函數，將粒子群算法運用到求解線形小區天線位置優化問題的過程中。仿真結果表明：基于粒子群優化算法搜索得到的次優位置能夠很好地逼近天線分布的最優位置，其誤差能夠控制在一定范圍以內；并且相對于計算機搜索，粒子群搜索可以大大降低計算的復雜度，能夠有效解決天線位置的分布問題。此外，綜合線形小區仿真結果還可以得出結論：影響天線最優位置的主要因素是基站側天線端口數目、天線布局方式以及用戶位置分布等三大系統參數。

[1]Wang X, Zhu P, Chen M. Antenna location design forgeneralized distributed antenna systems[J].Communications Letters, IEEE, 2009, 13(5): 315-317.

[2]韓亮,柳鑫,唐友喜等.線型小區中V-BLAST兩根分布發射天線的位置優化[J].電子與信息學報,2010,32(4): 978-982.

[3]Shen Y,Tang Y,Kong T,et al.Optimal antenna location for STBC-OFDM downlink with distributed transmit antennas in linear cells[J].Communications Letters,IEEE,2007,11(5):387-389.

[4]Firouzabadi S, Goldsmith A. Optimal placement ofdistributed antennas in cellular systems[C].SignalProcessing Advances in Wireless Communications(SPAWC), 2011 IEEE 12th International Workshop on.IEEE, 2011: 461-465.

[5]鄭娜娥,王大鳴,崔維嘉.一種分布式MIMO系統的快速天線選擇算法[J].計算機工程與應用,2011,47(22): 99-101.

Antenna Port Placement Optimization of Distributed MIMO System in Linear Cell

Fu Minghao,Li Yueheng
(College of Computer and Information,Hohai University,Nanjing,211100,China)

The research on the antenna port(AP)placement optimization of distributed multiple-input multiple-output(DMIMO) system in a linear cell has a very important practical significance.It discusses the optimal placement problem of base station antennas in DMIMO systems to maximize the cell average ergodic capacity.In the light of simulation results,it can be concluded that:the search based on Particle Swarm Optimization(PSO)can solve the optimization problem effectively.On the other hand,the main factors that affect the optimal antenna location include:the distribution of the user's location,the layout of the base station antennas and the number of antenna ports,and so on.

Distributed Multiple-Input Multiple-Output;Particle Swarm Optimization;Average Ergodic Capacity;Antenna Port Placement Optimization

TP311

A

1007-757X(2015)06-0032-03

2015.01.16）

付明浩（1991-），河海大學，計算機與信息學院，碩士研究生，研究方向：現代無線通信網絡、MIMO系統，南京，211100

李岳衡（1971-），河海大學，計算機與信息學院，教授，博士，研究方向：移動通信中的多天線傳輸理論與技術、現代無線傳感網絡協同信息獲取與處理，南京，211100