濕陷性黃土的微結構參數
王秀偉,高凌霞,武志東
(大連民族學院土木建筑工程學院遼寧大連116605)
濕陷性是黃土最為重要的工程性質,大量的研究表明,黃土的微觀結構是表征黃土濕陷性的一個重要質量指標[1-6]。在黃土微結構研究中,近年也取得了不少成果。尹亞雄[7]等采用掃描電鏡、數字圖像方法和表面積孔隙分析儀研究了天然黃土和不同固化齡期加氣硅化黃土的微結構和孔隙特征,Hu[8]等研究了黃土在動荷載壓密條件下的力學性能和微結構變化。倪萬魁[9]通過對洛川黃土在反復凍融作用下的電鏡掃描觀測、單軸壓縮試驗和三軸剪切試驗,研究了凍融循環作用對黃土微結構和強度的影響。王慧妮等[10]基于計算機X射線斷層術與掃描電鏡圖像對黃土微結構進行了定量分析。周陽等[11]利用改進的邊緣檢測算法,對黃土微結構SEM圖像進行檢測,該方法可以有效地去除虛假邊緣,區分黃土顆粒形態,從而更清晰地揭示其內部物質的結構。
綜上所述,基于掃描電鏡(SEM)的土體微觀結構研究是當前巖土工程中最有效、最直接的方法。本文針對原狀黃土進行了濕陷性試驗,SEM試驗,從中提取微結構參數,并對各參數間的相關關系進行統計分析。
1 黃土的濕陷性及電鏡掃描試驗
1.1 濕陷性試驗
試驗用土取自西安黃土塬區,取樣深度為2.0 m,原狀試樣。天然密度為 1.56 g.cm-3,土粒相對密度為 2.71,天然含水率為17.4%。采用單線法實驗確定黃土的濕陷性,實驗結果見表1。
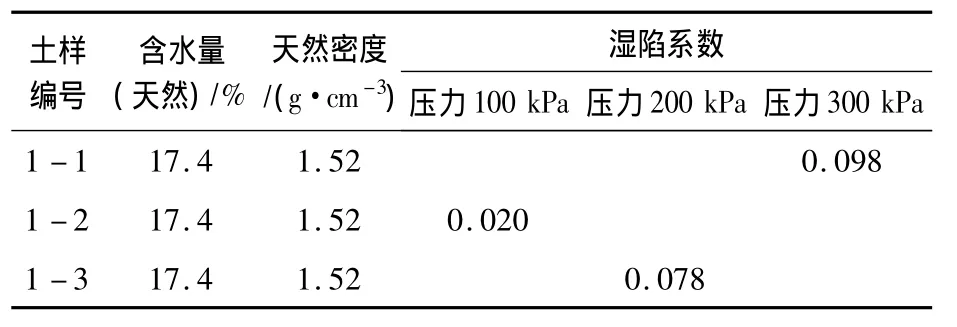
表1 天然含水量土樣濕陷試驗
1.2 SEM 試驗
采用掃描電鏡(scanning electron microscopy)獲取濕陷前后黃土的微結構照片。掃描電鏡被廣泛用來觀察土的微觀結構形態。本次試驗采用的掃描電鏡,不需干燥土樣,可以在自然狀態下觀察土樣的結構,這樣可減小對土樣的擾動。不同壓力作用下黃土濕陷前后的微結構照片如圖1。共獲得10幅濕陷前SEM照片和11幅濕陷后的照片。共21幅SEM照片組成的黃土樣本進行了域微結構分析。

圖1 濕陷前后的微結構SEM照片對比(左側為濕陷前的照片)
2 黃土微結構參數的相關分析
2.1 SEM圖像微結構參數的提取
對由10幅濕陷前SEM照片和11幅濕陷后的照片,共21幅SEM照片組成的黃土樣本進行了域微結構分析。采用Leica QWin系統可以提取到兩類微結構參數,域(Field)微結構參數和特征(feature)微結構參數[11]。本文針對9個域微結構原始參數進行研究。為了使得到的數據具有可比性和一般性,對所有照片的信息提取針對同一分析域進行,分析域的位置和大小(1200 μm×800 μm的矩形區域)如圖2。

圖2 SEM照片的研究域及參數定義
其中pi表示第i個孔隙,其水平截距為εi,垂直截距為νi,單位是像素,對于本分析過程,1μm=20像素。微結構參數提取后,每一個孔隙體對應一個9維向量。其中x1為水平截距,表示所有孔隙水平投影的長度之和,即x1=Σεi;x2為垂直截距,表示所有孔隙垂直投影的長度之和,即x2=Σνi;x3為所有孔隙的周長之和;x4為孔隙總數;x5為總孔隙面積百分比;x6為各向異性系數;x7為填充比;x8為平均弦;x9為圖像處理系統自動計算得到的256灰度自適應閾值。這些參數,從整體上反映了域內的孔隙體大小、形狀、級配、各向異性等微結構參數,基本刻畫了孔隙體微結構的所有信息。
2.2 微結構參數間的相關性研究
(1)簡單統計量
9維微結構參數可以表示為向量形式,即

得到的微結構參數的簡單統計量見表2。

表2 各參數的簡單統計量
(2)Pearson相關系數矩陣
由于9維微結構參數之間可能存在某種相關關系(包括正相關和負相關),為了研究這種相關性是否顯著,有必要考察參數間的相關系數矩陣。9維微結構參數之間的協方差矩陣可以表示為

將21組9維微結構參數代入式(4)和式(5),經過計算最終得到的協方差矩陣可以表示為

任意兩參數xj、xk之間的相關系數可以表示為

式(8)稱為Pearson相關系數矩陣,計算結果為

為判斷各參數之間是否相關,還要進行假設檢驗

給定顯著性水平α=0.0001,假設x為來自9維正態總體的一個樣本,根據統計學原理,如果H0為真,則

當p<α時,拒絕H0,否則接受H0。檢驗結果表明p16=0.1595,p26=0.0541,p36=0.0778,p46=0.1697,p56=0.1621 和p67=0.2218,p68=0.2205,p69=0.2432,均滿足p> α,說明二者之間的相關性不顯著。而對于其它各參數之間的相關系數,均滿足p<α,說明它們之間的相關性高度顯著。
(3)Spearman相關系數矩陣
微結構參數xi(i=1、2、…、9)是容量為21的一維樣本,即xi1、xi2、…、xin、…、xi21。其順序統計量為xi(1)、xi(2)、…、xi(m)、…、xi(21),若xin=xi(m),則稱m是xin在樣本觀測值中的秩,記作Rin,并稱Rin是第n個秩統計量。如果有多個大小相等的觀測值,其秩則為應排序位置的平均值。
根據上述方法,可以得到xi(i=1、2、…、9)的21個秩統計量。根據這些秩統計量,9維微結構參數可以改寫為以秩統計量表述的9×21矩陣。Spearman相關系數為秩統計量之間的相關系數,可以根據式(4)、式(5)和式(7)計算得到,但需要以Rin代替原始微結構數據。類似于Pearson相關系數矩陣,可以定義Spearman相關系數矩陣。即

與Pearson相關系數矩陣相比,Spearman相關系數矩陣似乎損失了某些信息,但它適用于研究具有一般分布的多維總體,且對有異常值的觀測數據,具有耐抗性。也就是說,個別數據的異常不會影響整體判斷結果。將原始參數代入以上各式,計算得到原始微結構參數的Spearman相關系數矩陣由式(14)表示。
同樣,給定顯著性水平α=0.0001,則當p<α時,拒絕H0,否則接受H0。檢驗結果表明p16=0.1228,p26=0.0238,p36=0.0432,p46=0.1244,p56=0.0896 和p67=0.0951,p68=0.1258,p69=0.1655,均滿足p>α,說明二者之間的相關性不顯著。而對于其它各參數之間的相關系數,均滿足p<α,說明它們之間的相關性高度顯著。這與前文Pearson相關系數的計算和檢驗結果是完全一致的。

由統計學得知,樣本數據的均值向量、協方差矩陣S及Pearson相關系數矩陣R,分別是總體的均值向量ˉx、協方差矩陣和相關系數矩陣的相合估計。而Spearman相關系數矩陣Q,則是總體相關系數矩陣的一個穩健估計。
3 結論
兩種相關分析的結果均表明,在所有孔隙體微結構參數之間,只有孔隙總面積和灰度自適應閾值之間的相關性不顯著,而其他參數之間的相關性均比較顯著。因此得出結論,在反映黃土微結構特性方面,提取到的參數有較多“重復”的信息。因此,在將土微結構參數引入土的本構模型中時,可以采用主成分分析,以消除這些“重復”,以降低參數的維數。
[1]謝定義.黃土力學特性與應用研究的過去、現在與未來[J].地下空間,1999,(4):273-284.
[2]胡瑞林,李向全,官國琳,等.土體微結構力學-觀念·觀點·核心[J].地球學報-中國地質科學院院報,1999,20(2):150-156.
[3]劉祖典,張伯平.關于黃土和黃土狀土濕陷性評價問題[J].西北農學院學報,1979,(03):37-48.
[4]高國瑞.黃土顯微結構分類與濕陷性[J].中國科學,1980,(12):1204-1208.
[5]高國瑞.中國黃土的微結構[J].科學通報,1980,(20):945-948.
[6]邵生俊,周飛飛,龍吉勇.原狀黃土結構性及其定量化參數研究[J].巖土工程學報,2004,26(4):531-536.
[7]尹亞雄,王生新,韓文峰等.加氣硅化黃土的微結構研究[J].巖土力學,2008,29(6):1629-1633.
[8]HU R L,YEUNG M R,LEE C F,et al.Mechanical behavior and microstructural variation of loess under dynamic compaction [J].Engineering Geology,2001,59(3-4):203-217.
[9]倪萬魁,師興強.凍融循環作用對黃土微結構和強度的影響[J].冰川凍土,2014,36(4):922-927.
[10]王慧妮,倪萬魁.基于計算機X射線斷層術與掃描電鏡圖像的黃土微結構定量分析[J].巖土力學,2012,33(1):243-254.
[11]周陽,王鳳,馬逢清,等.基于改進邊緣檢測算法的圖像處理技術應用[J].工業控制計算機,2013,26(3):73-77.

