單通道控制的旋轉彈錐形運動穩定性研究①
石忠佼,謝浩怡,林 蔚,趙良玉,3
(1. 北京理工大學 宇航學院,北京 100081;2. 中國北方工業公司,北京 100053;3.飛行器動力學與控制教育部重點實驗室,北京 100081)
?
單通道控制的旋轉彈錐形運動穩定性研究①
石忠佼1,謝浩怡1,林 蔚2,趙良玉1,3
(1. 北京理工大學 宇航學院,北京 100081;2. 中國北方工業公司,北京 100053;3.飛行器動力學與控制教育部重點實驗室,北京 100081)
錐形運動是旋轉彈角運動的基本形式,其穩定性問題一直是旋轉彈領域的研究熱點。以一對鴨舵作用下的單通道控制旋轉彈為研究對象,給出了彈體坐標系下的線性化角運動模型,通過數值仿真,揭示了一對鴨舵帶來的氣動不對稱對其角運動特性的影響規律。利用勞斯判據,給出了解析形式的錐形運動穩定條件,該條件可等效為錐形運動穩定條件下的轉速范圍,不同轉速下的仿真結果證明了該穩定條件的正確性。在相同的轉速條件下,正弦式鴨舵的控制頻率在慢模態衰減頻率附近時,可誘發強烈的共振不穩定。研究結果可為一對鴨舵作用下的旋轉彈總體設計及制導控制系統設計提供參考。
旋轉彈;氣動不對稱;穩定性;錐形運動;鴨舵
0 引言
旋轉彈是指在飛行過程中繞自身縱軸連續滾轉的一類彈箭飛行器,具有簡化控制系統結構和組成、避免不對稱燒蝕、放寬加工制造誤差容限、提高突防能力等一系列優勢,廣泛用于各類常規兵器、制導兵器、戰術導彈和再入飛行器等,代表著國內外裝備發展過程中的一個重要方向。常見的以空氣舵為控制力產生裝置的旋轉彈主要有2種:一種是以一對鴨舵為控制面的單通道控制方式,如美國的RAM防空導彈等;另一種是以2對鴨舵為控制面的雙通道控制方式,如國內的BRE3型制導火箭彈等。與非旋轉彈相比,旋轉彈俯仰和偏航通道間的氣動交聯、慣性交聯和控制交聯使其具有一些特殊的動力學特性,典型地表現在除了彈體繞自身縱軸的旋轉外,彈體縱軸還會繞其速度矢量做周期式劃圓運動,也就是常說的錐形運動。旋轉彈在飛行過程中的不穩定現象多數以不收斂的錐形運動形式出現,即彈體縱軸和速度矢量之間的夾角與其設計值的偏差不斷增大或維持一個較大的值不變。不收斂錐形運動引起的誘導阻力,將會大幅度削弱旋轉彈的設計性能,降低其完成預定任務的能力,嚴重時甚至會引起掉彈。這類現象在諸多無控和有控的旋轉彈上均有體現,如西班牙的140 mm火箭彈,在28次飛行試驗中出現了9次不收斂的錐形運動,使飛行速度在1.5 s內降低了60%[1]。國內在無控火箭彈[2]、有控火箭彈[3]的研制過程中也曾受到過不收斂錐形運動的困擾。因此,錐形運動穩定性的研究一直是旋轉彈領域的研究熱點。
目前,圍繞無控旋轉彈和雙通道控制旋轉彈的錐形運動穩定性問題已取得了豐富的研究成果,如Murphy[4]以一類無控對稱旋轉彈為例,創造性地在非旋轉彈體坐標系內建立了其動力學模型,并基于線性系統理論,獲得了錐形運動的穩定條件。楊樹興等[5]針對一類雙通道控制的旋轉體制火箭彈,在詳細揭示控制交聯產生機理的基礎上,分別建立了旋轉彈在多種類型自動駕駛儀作用下的彈體角運動方程,給出了錐形運動穩定的解析式條件,并指出執行機構的延遲,將嚴重影響控制回路設計參數的穩定邊界。但在單通道控制旋轉彈的錐形運動穩定性研究方面,研究成果尚顯不足。任天榮等[6]在RAM構型的單通道控制旋轉彈飛行實驗中,觀測到了足以影響性能指標的不收斂錐形運動。Cooper等[7]指出一對鴨式舵面存在的氣動不對稱,將導致旋轉彈出現不收斂的錐形運動,并采用數值方法,給出了其不穩定區域。
本文以Cooper等[7]的研究成果為基礎,利用勞斯判據,直接給出了一對鴨舵作用下的單通道控制旋轉彈錐形運動穩定條件,并采用數值仿真進行驗證,為單通道控制旋轉彈的錐形運動穩定性研究提供了另一種思路。同時,本文還修正了參考文獻[7]中的部分疏漏,研究成果對于單通道控制旋轉彈的轉速設計具有重要參考價值。
1 單通道控制旋轉彈的動力學特性
1.1 坐標系的定義
對于單通道控制的旋轉彈來說,由于其一對鴨舵的相位角之差為180°(大于2π/3),將不能忽略彈體旋轉引起的氣動不對稱性[8]。為了描述這種不對稱性對其角運動的影響,需要在隨彈體旋轉的彈體坐標系(簡稱為彈體坐標系,下同)內建立角運動方程。彈體坐標系的定義可描述為原點O位于彈體瞬時質心,Ox軸沿彈體對稱軸,且指向彈體頭部為正,Oy軸垂直于彈體對稱面,Oz軸由右手定則確定,且指向下為正,如圖1所示。
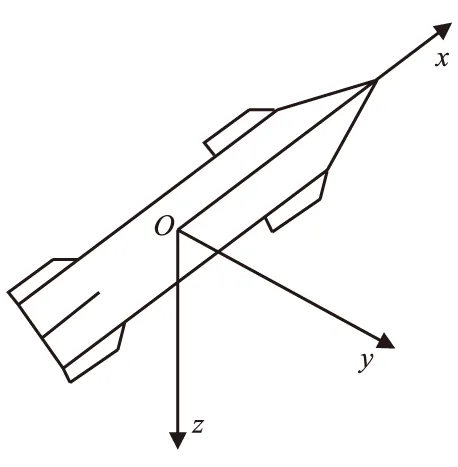
圖1 彈體坐標系示意圖Fig.1 Sketch of body coordinates
1.2 動力學模型
采用Cooper等[7]建立一對鴨舵控制旋轉彈的動力學建模方法,假設:
(1)彈體速度、轉速、質量以及空氣動力系數在小段時間內均保持不變;
(2)小角度假設,即有sinα=α,cosα=1,u≈V;
(3)攻角和側滑角可近似用式(1)計算:
(1)
由此得單通道控制旋轉彈的線性化角運動方程:
(2)
其中,系統矩陣T可表示為
A=πρD3CNA/(8m),B=πρpD5CYPALMAG/(16ITV)
C=πρD4CNALCO/(8IT),E=πρD5CMQ/(16IT)
F=pDIX/ITV,V2=-πρD3CNAC/(4m)
V3=πρD2ΔxcCNAC/(4m),M2=πρD4ΔxcCNAC/(4IT)
M3=-πρD3Δxc2CNAC/(4IT)
詳細的推導過程可參考文獻[7]。
式(2)中,V2、V3、M2和M3是非對稱氣動力的數學表現,如果將此4項設為0,就是對稱氣動布局旋轉彈的六自由度運動方程;δ為正弦式鴨舵偏轉函數,可表示為
δ=Δsin(kt),Δ=10°
(3)
分別對對稱旋轉彈(同時忽略非對稱氣動力和式(2)右邊第二項表示的非對稱控制力)、固定鴨舵旋轉彈(僅僅忽略非對稱氣動力)和具有活動鴨舵旋轉彈(完整式(2))的角運動特性進行數值仿真。選取轉速p=30 rad/s,控制頻率k=p。
圖2為上述3種情況下的角運動特性曲線,為便于觀察,將攻角和側滑角在非旋轉彈體坐標系上表示。非旋轉彈體坐標系上的攻角αN和側滑角βN可通過彈體坐標系上的攻角α和側滑角β變換得到,變換公式為
(4)
式中αN和βN為非旋轉彈體坐標系內的攻角和側滑角;φ為彈體滾轉角。
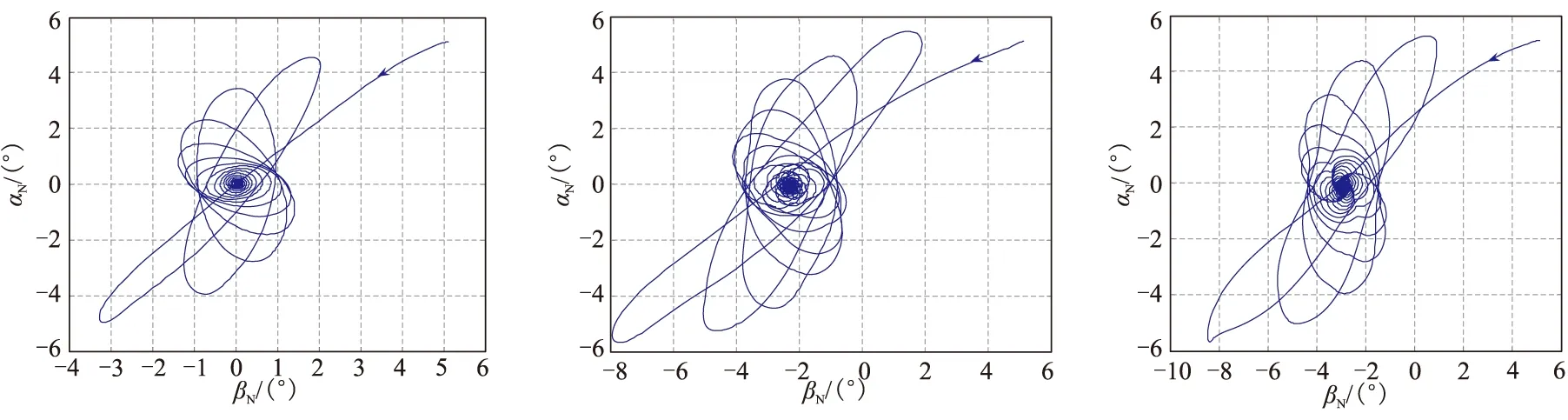
(a) 對稱旋轉彈 (b) 一對固定鴨舵旋轉彈 (c) 一對活動鴨舵旋轉彈
圖2 旋轉彈的角運動特性
Fig.2 Angular motion of spinning missiles
由圖2可見,在同樣的初始條件下,完全忽略氣動非對稱性時的穩態攻角為0°,僅僅考慮固定鴨舵產生的非對稱氣動力時的穩態攻角約為2°,正弦式鴨舵造成的穩態攻角約為3°。即對于這類一對鴨舵控制下的單通道旋轉彈來說,氣動非對稱性對其角運動特性具有重要影響,在研究其角運動特性時,必須考慮其氣動非對稱性。基于線性系統穩定性理論,可將式(2)右端第二項看作受迫擾動,通過系統矩陣T來考察其穩定性。
2 錐形運動穩定性分析
2.1 穩定條件
由式(2),系統矩陣可表示為如下格式:
(5)
特征方程可寫作:
Δ(λ)=b4λ4+b3λ3+b2λ2+b1λ+b0
(6)
式(6)中,各項系數如下:
(7)
根據勞斯判據,可得系統穩定的解析式充要條件為
(8)
由式(2)、式(5)、式(6)及式(7)可看出,對于指定的單通道控制旋轉彈來說,b4、b3、b2、b1和b0都是轉速p的函數,可將式(8)所示的錐形運動穩定條件等價為錐形運動穩定情況下的轉速取值范圍。
將表1所示的某型單通道控制旋轉彈的特征參數代入式(8),經轉換可得,錐形運動穩定條件下的轉速范圍為
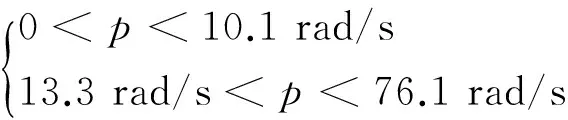
(9)
為驗證上述求解方法的正確性,選取不同的轉速進行數值仿真,相應的角運動特性如圖3所示。可看出,在p=12 rad/s時,旋轉彈的角運動在短時間內快速發散,系統不穩定;在p=30 rad/s時,旋轉彈的角運動在一段時間內收斂,系統穩定;在p=80 rad/s時,旋轉彈的角運動逐漸發散,系統不穩定。對比p=12 rad/s和p=80 rad/s時的發散速度,可推測系統這兩種轉速情況下具有不同的特征根實部,且p=12 rad/s時的特征根實部明顯更大。
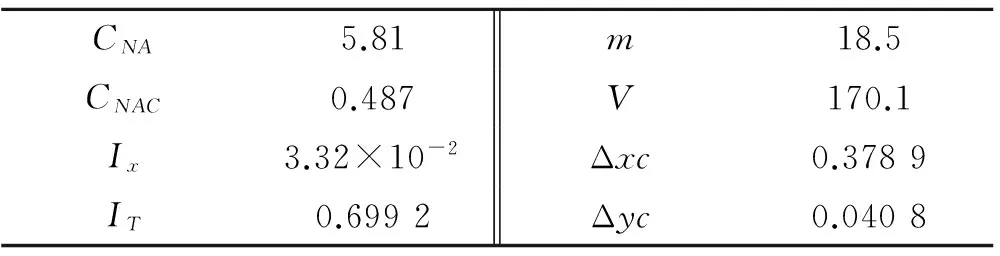
表1 彈體參數Table1 Parameters of a spining missile
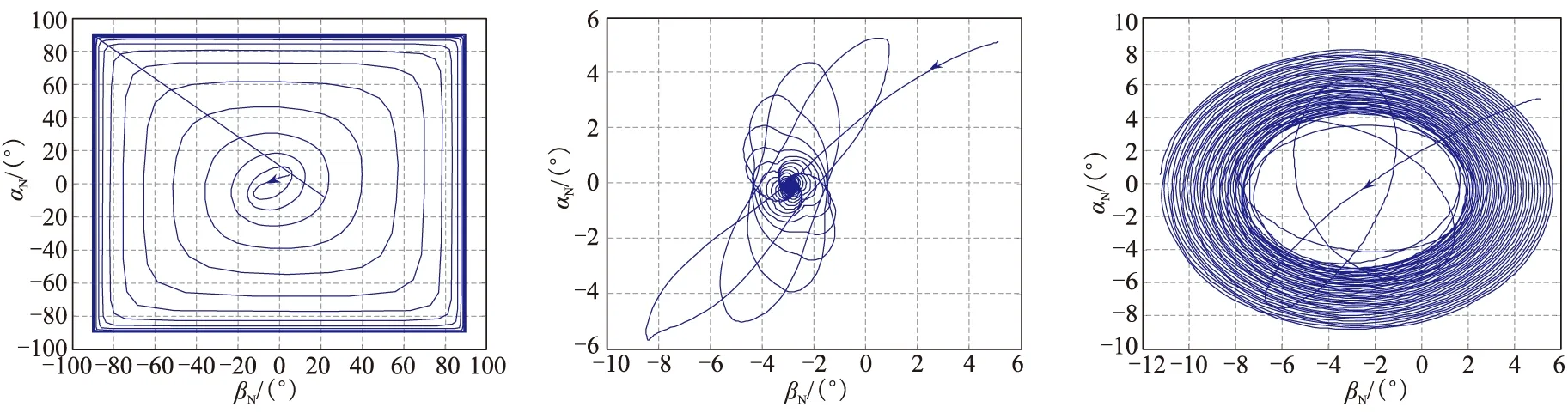
(a)p=12 rad/s (b)p=30 rad/s (c)p=80 rad/s
轉速p與特征根實部的關系如圖4所示。其中,慢模態曲線的尖點對應虛部為零的情況。需要指出的是本文快、慢模態的變化趨勢與文獻[7]不同。經分析可知,快模態的衰減幅度較大。所以,其實部絕對值應該大于慢模態實部絕對值,而不是文獻[7]中的慢模態實部絕對值大于快模態實部絕對值。
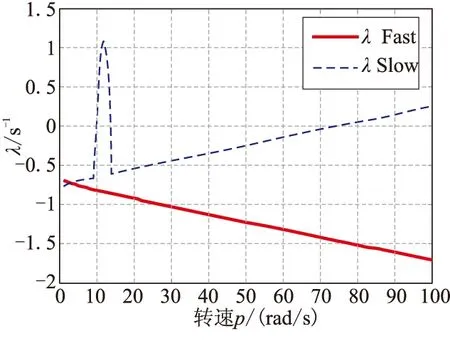
圖4 快模態和慢模態特征值實部vs轉速pFig.4 Real parts of fast and slow modes vs spin rate p
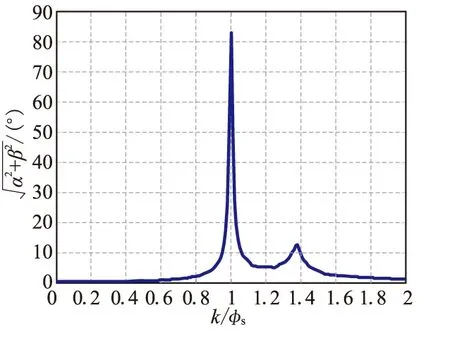
根據線性系統穩定的充要條件是系統特征根的實部為負數可知,在轉速滿足0 2.2 控制頻率對穩定性的影響 圖5 控制頻率k與全攻角曲線圖Fig.5 Change of full angle of attack with control frequency k 同樣,與文獻[7]不同,本文所得結論是當控制頻率k在慢模態衰減頻率附近時,將引起系統強烈的共振不穩定。從過渡過程角度分析,慢模態運動將主導過渡過程,故本文結果更符合物理事實。因此,在選擇旋轉彈的控制頻率時,要避開慢模態運動的衰減頻率,以避免系統出現共振不穩定。 (1)本文通過數值仿真,揭示了單通道控制旋轉彈的氣動非對稱性對彈體角運動特性的影響規律,一對正弦式鴨舵造成的穩態攻角約為3°。 (2)通過勞斯判據,給出了解析形式的錐形運動穩定條件,該穩定條件可方便的等價為錐形運動穩定情況下的旋轉彈轉速范圍,為單通道控制旋轉彈的錐形運動穩定性研究提供了另外一種思路,不同轉速下的數值仿真結果證明了該方法的正確性。 (3)單通道控制旋轉彈的錐形運動不穩定主要表現為慢模態運動的失穩,當控制頻率k在慢模態衰減頻率附近時,將引起系統強烈的共振不穩定。 [1] Morote J,Liao G.Stability analysis and flight trials of a clipped wrap around fin configuration[C]//AIAA Atmospheric Flight Mechanics Conference and Exhibit.Providence,Rhode Island,August 2004. [2] 趙良玉,楊樹興,焦清介.提高卷弧翼火箭彈圓錐運動漸近穩定性的幾個方法[J].固體火箭技術,2010,33(4):369-372. [3] Yan Xiao-yong,Yang Shu-xing,Zhang Cheng.Coning motion of spinning missiles induced by the rate loop[J].Journal of Guidance,Control,and Dynamics,2010,33(5):1490-1499. [4] Murphy C H.Free flight motion of symmetric missiles[R].U.S.Army Ballistic Research Laboratories,Rept.1216,1963. [5] Yan Xiao-yong,Yang Shu-xing,Xiong Fen-fen.Stability limits of spinning missiles with attitude autopilot[J].Journal of Guidance,Control,and Dynamics,2011,34(1):278-283. [6] 任天榮,馬建敏.基于陀螺力學的旋轉導彈錐形運動分析[J].宇航學報,2010,31(9):2082-2087. [7] Cooper G,Fresconi F,Costello M.Flight stability of an asymmetric projectile with activating canards[J].Journal of Spacecraft and Rockets,2012,49(1):130-135. [8] Murphy C H. Angular motion of spinning almost-symmetric missiles[J].Journal of Guidance,Control,and Dynamics,1979,2(6):504-510. (編輯:呂耀輝) Research on coning motion stability of a spinning missile with one pair of canards SHI Zhong-jiao1, XIE Hao-yi1, LIN Wei2, ZHAO Liang-yu1,3 (1.School of Aerospace Engineering, Beijing Institute of Technology, Beijing 100081, China;2.China North Industries Corp., Beijing 100053, China;3.Key Laboratory of Dynamics and Control of Flight Vehicle, Ministry of Education, Beijing 100081, China) The coning motion is a basic angular behavior of spinning missiles,and the research on the stability of coning motion has been the heated topic in the field of spinning missle.The linearized 6-DOF equations of angular motion for a spinning missile with one pair of canards were established in the rolling body frame. The influence of aerodynamic asymmetry due to the canards on the angular motion was revealed via numerical simulations.The analytical stability condition of coning motion was given by Routh criterion, which can be transformed to be an equivalent of rotation rate with stable coning motion. Simulations under different spinning rate demonstrate that the stability condition was reliable.In the case of a given spinning rate,the sinusoidal canard with activating frequency in the neighborhood of the slow mode can induce strong resonance instability.The research results can provide references to the system design, guidance and control design of spinning missiles with one single pair of canards. spinning missiles;aerodynamic asymmetry;stability;coning motion;canards 2014-04-12; :2014-05-21。 國家自然科學基金項目(11202023)。 石忠佼(1991—),男,碩士研究生,研究方向為飛行器動力學與控制。E-mail:371088433@bit.edu.cn 趙良玉(1981—),男,博士/副教授,研究方向為飛行器總體設計。E-mail:zhaoly@bit.edu.cn V411 A 1006-2793(2015)02-0156-04 10.7673/j.issn.1006-2793.2015.02.002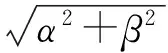
3 結論

