基于相關性理論確定影響高速公路路基工程量的技術指標

■林 果

（福建省交通工程造價管理站，福州 350001）

0 引言

高速公路工程建設項目相對于一般土建項目而言，是一個周期長、投資大、技術標準高、受地質和天氣影響大、較為復雜的生產消費過程，期間需要消耗大量的人工、材料、機械及生活資料。據相關統計，福建省高速公路每公里需消耗水泥14000t、 鋼材2500t、 瀝青550t、 礦石料6 萬m3、 油料600t、 用地需求量每公里100 畝。而在公路工程項目建設的整個投資過程中，設計成本控制尤為重要。路基工程量是高速公路工程量的重要組成部分，路基工程主要工程量包括有土石方、防護工程、排水工程。在設計階段，相似地形下路基工程量受到各種技術指標的影響， 不同的設計技術指標將直接影響工程量的大小。

以福建省已修建的高速公路為統計數據，統計區段內的路基典型工程數量及技術指標；技術指標統計為：路線增長系數、最大直線長度、最大縱坡長度、最大縱坡、綜合平曲線半徑、綜合豎曲線半徑、平曲線比例、豎曲線比例。在福建省已修建完成的高速公路中微丘地形下四車道設計時速為80km/h 的高速公路樣本數最多，采用該樣本作為數據進行分析。

1 相關性分析

1.1 分析理論

相關性分析[1]（Correlation analysis）是指對兩個或多個具備相關性的變量元素進行分析， 從而衡量兩個變量因素的相關密切程度。 相關性的元素之間需要存在一定的聯系或者概率才可以進行相關性分析。 相關關系反映出變量之間雖然相互影響，具有依存關系，但彼此之間是不能一一對應的。

相關性分析其實就是觀察一下各個指標的相關程度。 一般來說相關性越是高， 做主成分分析就越是成功。評價相關性的方法就是相關系數，由于是多變量的判定，則引出相關系數矩陣。相關分析所用的指標是相關系數及對應的顯著性水平。相關系數r 是反映兩變量之間相關關系密切程度的統計量、變量之間的線性相關程度，其取值在-1～1 之間；顯著水平是相關系數的可靠程度，其取值在0～1 之間。具體說明如下：

（1） 當0＜|r|＜1 時， 表明變量之間存在一定的線性相關關系。若r＞0，表明變量之間為正相關；若r＜0，表明變量之間為負相關。

（2）當r=0 時，表明變量之間無線性相關關系，但兩者間依然可能可以存在非線性的相關關系。

（3）對于相關性檢驗結果一般遵循的原則如下：

①相關系數滿足：0＜|r|＜1；

②Sig.（雙側顯著性水平值）＜α（預定的顯著性水平）；

SPSS 軟件[2]共提供了3 種相關性檢驗的方法，分別是Pearson（皮爾遜） 法、 Kendall（Kendall's tau-b）（肯德爾） 法及Spearman（Spearman's rho） （斯皮爾曼）法，3 種方法的使用條件有所不同[3]，具體如下：

Pearson 相關系數法一般要求變量是正態分布， 沒有奇異值影響。由于統計數據中設計技術指標大多數并不服從正態分布，因此，在本文中并未采用Pearson 相關系數進行相關性檢驗。

Kendall 法要求每個評價者都能對N 件事物 （或作品）好壞、優劣、喜好、大小、高低等排出一個等級順序，即大致能夠對每一個x 對每一個y 的影響排序，這一點是較為困難的， 因此， 在本文中并未采用Kendall（Kendall's tau-b）相關系數進行相關性檢驗。

由于Spearman 對原始變量的分布不作要求， 屬于非參數統計方法，適用范圍較廣。因此，在本文最終采用Spearman（Spearman's rho）相關系數進行相關性檢驗。

1.2 Spearman（Spearman's rho）相關系數法

又稱秩相關系數、 等級相關系數， 或順序相關系數[3]，對不服從正態分布的、一側開口、總體分布類型未知等不符合使用積矩相關系數來描述關聯性 （即不采用Pearson 相關系數法）的數據較為適用。Spearman 法采用秩相關（也稱等級相關） （rank correlation），來描述兩個變量之間的關聯程度與方向， 其計算方法與Pearson法公式形式很相似，但有所不同，如公式(1)所示。

式中，Ri（或Si）——第i 個x（或y）值的秩；

1.3 工程量與技術指標樣本合理區間

由于高速公路工程項目具有線長、量大、單一性特殊性明顯等特點， 為了統計樣本更具代表性， 需進行“典型工程量”合理區間的確定，剔除統計過程中不合理的樣本。高速公路微丘地區140 個樣本，將樣本中每個 “典型工程量”進行排序，作出其散點圖，由點構成的曲線越接近水平的直線就說明這一區域集中程度越高，反之越低；點與點之間越緊密說明這一區間連續性越好，技術指標集中程度越高，反之越小。故計算出點與點間的相差度a 就能知道點與點的連續性，相差度a由以下公式進行計算。

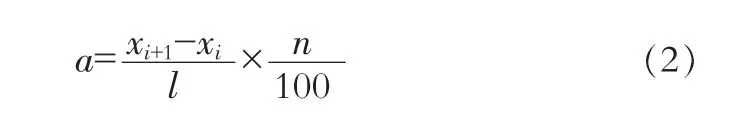
式中，xi+1、xi——表示某一技術指標相鄰兩點的指標；

l——表示該技術指標的樣本區間長度；

n——表示樣本的總數。

由于統計分析可得，當樣本數為100 時，相差度小于0.01 時， 表明相差度在合理范圍內， 當相差度小于0.005 時，表明相差度比較小，樣本集中程度比較明顯，當相差度大于0.01 時，表明相差度不在合理范圍內，集中程度較弱；當相差度大于0.05 時，表明相差度極度偏離合理范圍內，相應的點應當予以剔除。結合上述理論可確定 “典型工程量”合理區間，計算出合理區間的范圍（上限-下限）、合理區間的范圍的比例以及合理區間內樣本個數。高速公路微丘設計時速80km 工程量合理區間如下表1。區間范圍結果如圖1～圖3 所示。

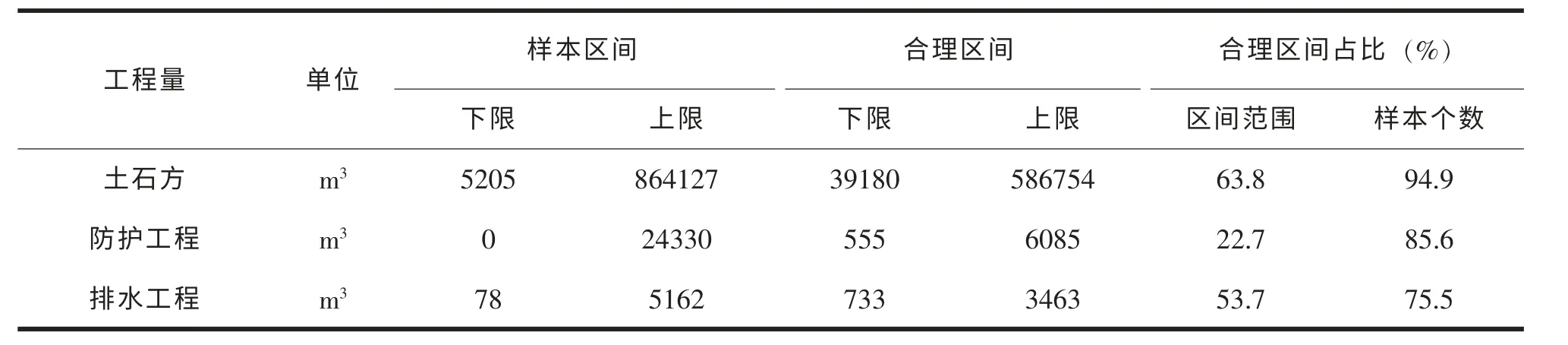
表1 微丘工程量合理區間表

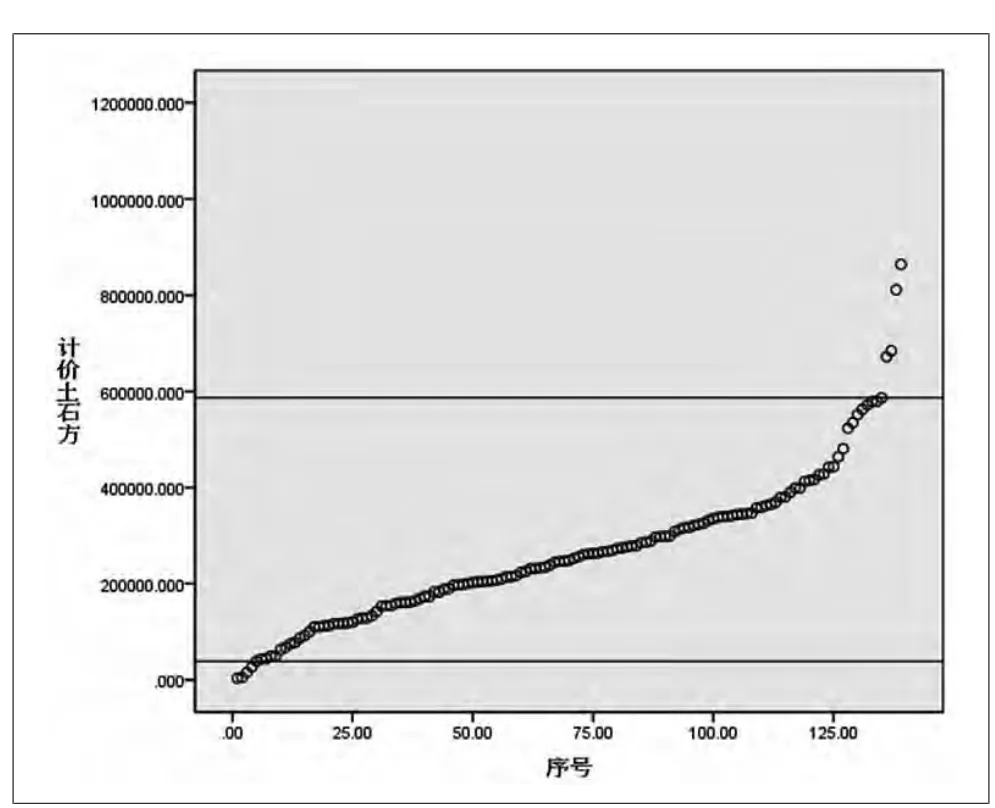
圖1 計價土石方排序散點圖

圖2 防護工程排序散點圖

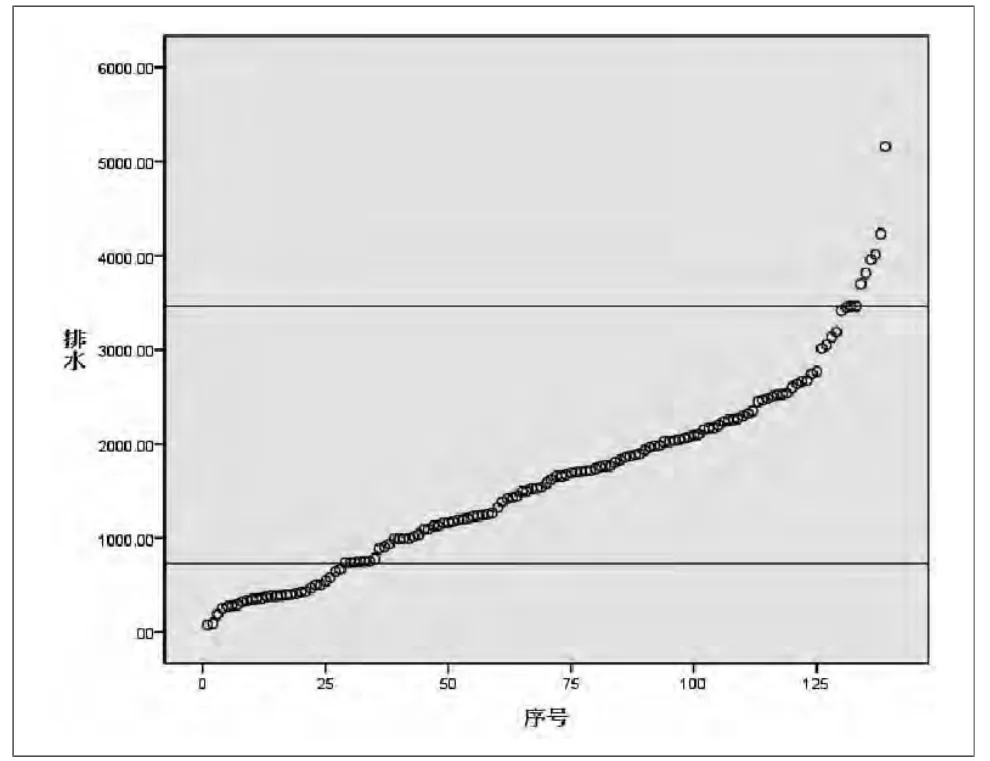
圖3 排水工程排序散點圖

對上述結果進行研究分析發現，在較小的區間內，包含了絕大多數的樣本，這說明樣本集中在一個較小的區域內，該區間能很好的反應樣本集中的這一特性，能基本滿足應用要求。即可確定為工程量的合理區間。

1.4 工程量與技術指標相關性分析

一般在進行相關性分析時， 通過兩組數據之間的“相關系數”及 “顯著性水平 （雙側）”2 項數值共同判斷兩者之間的相關關系。判定法則如下：

（1）通過相關系數的取值，比較相關系數值是否與1 較為接近，大致判定兩組數據之間是否可能存在近似線性相關的關系。

（2）通過顯著性水平 （Sig.）取值，判定 （1）中所得出的兩組數據之間的相關關系是否值得信賴。在數學分析中，一般取0.05（雙側）為相關性分析的判定分界值，即當兩組數據顯著性值≤0.05 時，認為該兩組數據具有顯著的相關關系 （相關關系值得信賴）。

由于高速公路工程項目線長、點多、受地形、地質等各種因素交互影響，工程數量會因為實際情況的不同而產生一定偏差，因此在研究分析中，可以考慮一定程度上降低判別標準，本文將相關分析的顯著性水平最大放寬值0.15（雙側）， 分析過程中共采用了0.01（雙側）、0.05（雙側）、0.10（雙側）、0.15（雙側），共4 檔不同的顯著性水平。將合理區間內 （見表1）樣本 “路基典型工程量數據”三個指標與相應的 “設計技術指標數據”八個指標分別錄入SPSS 軟件，進行技術指標與工程量建立相關性分析。設計技術指標與標準路基典型工程量的相關分析情況如表2 所示。

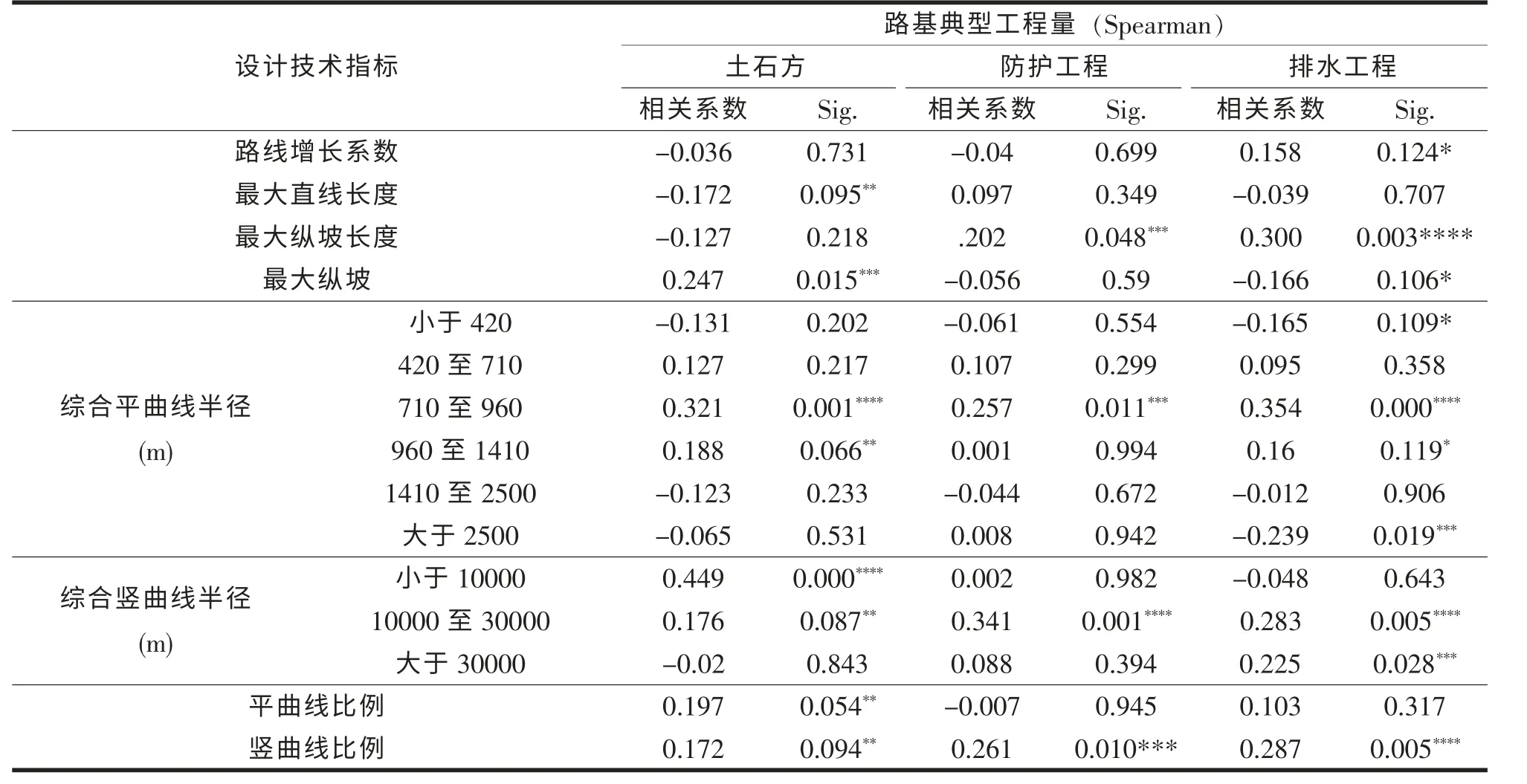
表2 設計技術指標與路基典型工程量的相關分析結果

由表2 可知：①與各項工程量具有顯著相關關系的技術指標不止一個，即各項工程數量的多少取決于多個主要指標的共同制約；②各個與工程數量顯著相關的技術指標的相關系數均較小 （<0.50），這些技術指標與相應工程數量之間的關系均為非線性關系。

2 相關性分析結果及應用

2.1 相關性分析結果

對表2 數據進行整理，將Spearman（Spearman's rho）相關系數進行相關性檢驗結果中，在0.01（雙側）、0.05（雙側）、0.10（雙側）、0.15（雙側）4 檔不同的顯著性水平條件下，具有顯著相關關系的“設計技術指標”與“路基典型工程量”進行匯總，具體情況如表3 所示。

如果考慮到以上設計技術指標中歸類，一定區間內平（豎）曲線半徑個數統計值受制約影響因素較多可以合并， 因此， 將剩余指標列為各項路基典型工程量的“主要指標”，如表4 所示。

表3 設計技術指標與路基典型工程量的相關分析結果

表4 各路基工程量的主要指標匯總

在確定與 “路基典型工程量”具有顯著相關關系的“設計技術指標”后，按照顯著性水平由高到低 （Sig.值由小到大），對影響各項 “路基典型工程量”的 “設計技術指標”進行排序，排序靠前的 “設計技術指標”即為影響 “路基典型工程量”的 “主要指標”， “主要指標”的確定為后期建立 “路基典型工程量”與 “設計技術指標”中的“主要指標”間的關系奠定了基礎。

2.2 應用實況

（1）構建預測模型

根據相關性分析表4 結果， 以0.05（雙側） 為例，各工程量對應相關性較顯著的技術指標，其模型建立過程中以Yi-j表示第i 個工程表與第j 技術指標間的函數關系，具體情況如表5 所示，Y1、Y2、Y3分別表示工程量計價土石方、防護、排水。

表5 擬合模型因變量表

運用MATLAB 軟件，錄入微丘地形、設計速度為80km/h 條件下，各個樣本的技術指標及工程數量統計值， 依據相關性分析結果： 對于土石方， 選取最大縱坡、綜合平曲線半徑及豎曲線半徑為主要技術指標，對于防護工程和排水工程，選取最大縱坡長度、豎曲線長度、綜合平曲線半徑及豎曲線半徑為主要技術指標，即自變量，通過MATLAB 擬合工具箱，分別確定擬合程度最高的一元函數模型。將Yij錄入到spss 中進行二次擬合，得到綜合模型。重復以上過程，進行多次嘗試，找到擬合程度最好的模型。分別得出土石方工程、防護工程、排水工程與相關技術指標的關系函數。交通工程造價管理人員可以在優化技術指標時快速估算出路基工程量。也為造價管理部門的造價審查提供方便和科學依據。

（2）優化設計指標配置

從近年來設計情況看，總體上設計指標還存在配置不盡合理，仍有優化空間。因此，可以通過給出了不同置信區間內影響高速公路典型工程量的主要技術指標，加強對公路線形設計指標配置的剖析，達到減少工程數量，節省工程造價的目的。

3 小結

通過高速公路優化設計的應用表明，優化方案值得應用和推廣，經過我省11 條高速公路應用的分析與統計，測設里程449.8km，初編概算438 億元，節省費用29.14 億元，取得明顯的經濟效果。

[1]王愛蓮.統計學.第七章 相關與回歸分析.第一節 相關分析.西安石油大學,經濟管理學院.

[2]鄧維斌，唐興燕.SPSS 統計分析軟件19（中文版）[M].電子工業出版社，2012.3.

[3]徐維超.相關系數研究綜述[J].廣東工業大學學報,2012(03).