匿名性可撤銷的高效環(huán)簽名構(gòu)建

程小剛，郭 韌，陳永紅

（1.華僑大學(xué) 計(jì)算機(jī)科學(xué)與技術(shù)學(xué)院，福建 泉州362021；2.華僑大學(xué) 工商管理學(xué)院，福建 泉州362021）

0 引 言

環(huán)簽名［1］是指一群中任一用戶可在群成員中任選一個(gè)包含自己的子集，做出簽名，之后任何人可驗(yàn)證此簽名的確由此子集中的某個(gè)人所簽署 （不可偽造性），但不能分辨出到底是誰簽的 （匿名性）。

環(huán)簽名最早的應(yīng)用是匿名消息發(fā)布，如一不愿透露身份的某組織高層可利用此機(jī)制向新聞界發(fā)布一個(gè)消息，記者們可驗(yàn)證此消息的確是由某高層權(quán)威發(fā)布，但不能分辨出到底是哪一位，還可簡(jiǎn)單實(shí)現(xiàn)指定驗(yàn)證者簽名 （designated verifier signature，DVS），即簽名只能由發(fā)布方指定的驗(yàn)證者才能驗(yàn)證其合法性，其他人都不行，利用環(huán)簽名機(jī)制很容易實(shí)現(xiàn)DVS簽名，只要發(fā)布方發(fā)布一個(gè)包含自己和驗(yàn)證方的環(huán)簽名即可，驗(yàn)證方知道自己未簽署此消息，所以只可能是發(fā)布方簽署的，但外界對(duì)此簽名則分不清到底是兩人中誰簽的。

早期的環(huán)簽名方案效率較低，尤其是簽名大小通常是O（k），k是子集成員數(shù)目，即簽名大小線性依賴于子集的大小，這對(duì)大規(guī)模環(huán)簽名的應(yīng)用是個(gè)大問題；也有作者構(gòu)造了一個(gè)簽名大小為常數(shù)的環(huán)簽名方案，但其安全性基于ROM模型，而ROM模型近來又收到一些學(xué)者的批判；Chandran等構(gòu)建了在標(biāo)準(zhǔn)模型下安全的環(huán)簽名方案［2］，但其簽名大小為O（k1／2），效率較低；近來一些學(xué)者將基于身份的密碼技術(shù)用于環(huán)簽名構(gòu)建［3－7］，但這些基于身份的環(huán)簽名方案存在 “密鑰托管”的問題，即密鑰分發(fā)中心掌握所有人的密鑰，因而其可以冒充任一用戶進(jìn)行環(huán)簽名，且一旦密鑰分發(fā)中心被黑客攻破，整個(gè)系統(tǒng)崩潰；也有學(xué)者提出了在標(biāo)準(zhǔn)模型下基于格的環(huán)簽名方案［8，9］，但簽名大小也依賴于環(huán)的大小，效率較低。

本文基于群結(jié)構(gòu)保持簽名 （structure preserving signa－ture，SPS）［10］與 Groth－Sahai證明系統(tǒng)［11］構(gòu)建了一個(gè)標(biāo)準(zhǔn)模型下安全、簽名大小為常數(shù)的環(huán)簽名方案，同以前的環(huán)簽名方案相比，增加了一個(gè)環(huán)管理員 （ring manager，RM）角色和一個(gè)用戶加入過程，解決了基于身份的環(huán)簽名中的“密鑰托管”問題；方案中簽名／驗(yàn)證的效率較高，達(dá)到了“近似常量級(jí)”的計(jì)算效率，對(duì)于大的環(huán)來說效率遠(yuǎn)優(yōu)于現(xiàn)有標(biāo)準(zhǔn)模型下的方案 （因大都線性依賴于環(huán)的大小）；由于RM角色的存在，環(huán)簽名的匿名性在出現(xiàn)爭(zhēng)議的情形下，可由RM來撤銷掉，找出真正的簽名者；構(gòu)建中采用了模塊化的密碼系統(tǒng)構(gòu)建思想，使得方案的安全性分析與驗(yàn)證較為直接。黃大威等也構(gòu)建一個(gè)匿名性可撤銷的環(huán)簽名方案［12］，但其構(gòu)建是基于ROM模型的，而所提構(gòu)建是基于標(biāo)準(zhǔn)模型的。

1 定義與數(shù)學(xué)假設(shè)

下面我們給出匿名性可撤銷環(huán)簽名的定義與所用到的數(shù)學(xué)假設(shè)：

定義1 我們的環(huán)簽名方案由下列5個(gè)多項(xiàng)式時(shí)間算法構(gòu)成：

（1）Setup：RM根據(jù)給定的安全參數(shù)，生成環(huán)的主密鑰和公開參數(shù)PP；

（2）Join：RM和用戶之間執(zhí)行一交互協(xié)議，之后成員獲得證書和私鑰成為環(huán)成員 （可生成環(huán)簽名），RM更新相關(guān)數(shù)據(jù)結(jié)構(gòu)并公布成員的公鑰，以接納此用戶成為環(huán)成員；

（3）Sign：環(huán)成員可任選環(huán)成員的一個(gè)子集R（包含其自身），利用R中成員的公鑰、環(huán)公開參數(shù)PP和其自身的證書與私鑰生成環(huán)簽名；

（4）Verify：任何人由PP及R的描述與R中成員的公鑰，可驗(yàn)證某一環(huán)簽名是否合法 （即簽名由R中某成員生成，雖然不能判斷到底是誰）；

（5）Open：在出現(xiàn)爭(zhēng)議的情況下，RM可打開某合法的環(huán)簽名，找出真正的簽名者。

注意同一般的環(huán)簽名定義相比，我們的方案中有一管理員負(fù)責(zé)環(huán)成員的加入；但我們的方案維持了環(huán)簽名的核心概念：自主選擇的匿名性。

定義2 DLIN （decision linear）假設(shè)：在階為大素?cái)?shù)p的群中，給定一個(gè)隨機(jī)的生成元g、（ga，gb，gac，gbd），其中a，b，c，d∈Z＊p是隨機(jī)的，分辨隨機(jī)元素T或T＝gc＋d是困難的。

定義3 SDH （strong Diffie－Hellman）假設(shè)，在階為大 素 數(shù) p 的 群 中， 給 定 （g，ga，ga2，…，gan）， 生 成（g1／（a＋c），c）是困難的。

定義4 SDP （simultaneous double pairing）假設(shè)：在對(duì)稱雙線性群 （G，GT）中，給定 （gz，gr，hz，hu）∈G，找到非 平 凡 的 （z，r，u）∈ G，滿 足e（gz，z）e（gr，r）＝ 1 且e（hz，z）e（hu，u）＝1是困難的。

注意DLIN假設(shè)是蘊(yùn)含SDP假設(shè)的［13］。

2 工 具

（1）群結(jié)構(gòu)保持簽名

群結(jié)構(gòu)保持簽名 （SPS）指的是此種簽名方案中，簽名、公鑰、消息都是雙線性群中的元素，而對(duì)簽名的驗(yàn)證只是驗(yàn)證一些雙線性對(duì)乘積方程 （pairing product equation，PPE）是否成立。定義SPS簽名的目的在于其可與Groth－Sahai證明系統(tǒng)［11］很好的融合，來零知識(shí)證明我有一個(gè)簽名 （如某個(gè)CA頒發(fā)的證書），因而可用于許多需要匿名或隱私保護(hù)的場(chǎng)合。

近來Abe等提出一個(gè)十分高效 （簽名大小為O（1））的SPS方案［10］，安全性基于標(biāo)準(zhǔn)的DLIN假設(shè)。此SPS方案基于 TOT （tagged one－time）簽名和rSIG （RMA－secure）簽名方案：

Setup：生成TOT公私鑰對(duì) （pkt，skt）和rSIG公私鑰對(duì) （pkr，skr）；

Sign：對(duì)待簽消息msg，先選隨機(jī)的tag用TOT對(duì)msg簽名δt＝TOT.Sign （skt，msg，tag），在用rSIG對(duì)tag簽名δr＝rSIG.Sign （skr，tag），最后的簽名為δ＝ （tag，δt，δr）；

Verify：只要驗(yàn)證簽名中的兩種簽名都是合法的即可。

TOT就是對(duì)某個(gè)消息簽名之前先生成一個(gè)隨機(jī)的標(biāo)簽（tag），再用此標(biāo)簽來對(duì)消息簽名，只要此標(biāo)簽只使用一次，那么此簽名方案是安全的；rSIG就是只要所簽的多是隨機(jī)消息，那么方案是安全的；上述SPS構(gòu)造就是先用TOT和一隨機(jī)標(biāo)簽對(duì)消息簽名，再用rSIG對(duì)標(biāo)簽進(jìn)行簽名；基于DLIN假設(shè)Abe等構(gòu)造了常數(shù)大小的TOT和rSIG方案［10］，綜合起來就得到常數(shù)大小的SPS簽名。

（2）Groth－Sahai證明系統(tǒng)

Groth－Sahai證明系統(tǒng)是第一個(gè)標(biāo)準(zhǔn)模型下、高效的NIWI／NIZK證明系統(tǒng)，可用于證明一大類在雙線性群中的二次方程。其安全性可基于各種不同的數(shù)學(xué)假設(shè)如DLIN、SXDH和子群分辨等，這里我們介紹基于DLIN假設(shè)的實(shí)現(xiàn)。

首先要生成大素?cái)?shù)階的雙線性群e：G×G→GT，并設(shè)置CRS（common reference string）為其中要對(duì)X∈G進(jìn)行承諾的話，計(jì)算其中⊙表示向量中對(duì)應(yīng)元素相乘，能設(shè)置成兩種不同而又計(jì)算上 “不可分辨”的形式，而分別給出 “完全正確”和“證據(jù)不可分”的結(jié)果：在 “完全正確”的情況中，設(shè)置因而C是X的DLIN加密，可通過β1＝loggf1，β2＝loggf2進(jìn)行解密得到唯一的那個(gè)X；而在 “證據(jù)不可分”情景下，設(shè)置成是線性獨(dú)立的，因而C是一個(gè)完全隱藏的承諾 （即X被完全隱藏）；而基于DLIN假設(shè)，這兩種情況 （兩個(gè)不同的）是計(jì)算不可分的。

要對(duì)Zp中的元素x進(jìn)行承諾的話，計(jì)算C＝用同上面類似，ψ可被設(shè)置成兩種不同而又計(jì)算不可分的值以分別實(shí)現(xiàn) “完全正確”和 “證據(jù)不可分”。要實(shí)現(xiàn) “正確性”，是線性獨(dú)立的；要 “證據(jù)不可分”，設(shè)得到一個(gè)完全隱藏的承諾，因?yàn)榇藭r(shí)不管x是多少，C都是1的DLIN加密。

要證明一些 “承諾”中的變量滿足一組二次方程，證明者要對(duì)每個(gè)方程生成一個(gè)NIWI／NIZK證明 （此證明可能包含多個(gè)群元素）。

對(duì)雙線性群中的PPE方程和 MEE （multi－exponential equation）方程，存在這樣的NIWI／NIZK證明，PPE就是

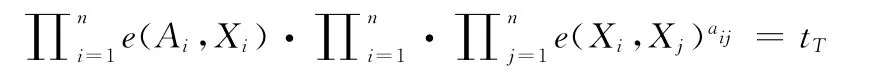
其中X1，…Xn∈G是變量，tT∈G，A1，…An∈G，aij∈Zp是常量。

而MEE方程是指

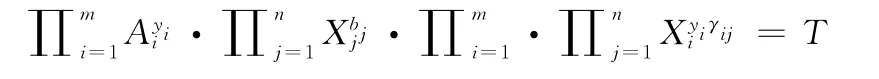
其中X1，…Xn∈G，y1，…ym∈Zp是變量，T，A1，…Am∈G和γij，b1，…bn∈Zp是常量

3 構(gòu) 建

下面是我們的環(huán)簽名的構(gòu)建：

（1）Setup：RM生成階為素?cái)?shù)p的雙線性群e：G×G→GT，選隨機(jī)的x1，…，xn∈Zp，y1，…，yn∈Zp設(shè)置環(huán)公鑰rpk＝ ｛G1，…，Gn；H1，…，Hn｝＝ ｛gx1，…，gxn；hy1，…，hyn｝，RM 私鑰為rsk＝ ｛x1，…，xn；y1，…，yn｝；初始化成員列表User＿List＝；生成上述SPS簽名的公私鑰對(duì)，并發(fā)布對(duì)G1，…，Gn；H1，…，Hn的簽名；

（2）Join：RM與用戶i之間執(zhí)行一交互協(xié)議，具體可參見Groth［14］，之后用戶成為環(huán)中一員，RM得到其公鑰Vi，而成員得到私鑰si，滿足關(guān)系Vi＝gsi；GM添加 （Vi，Vxii）和（Vi，Vyii）到User＿List中去；

為提高簽名和驗(yàn)證效率，RM同同時(shí)公布e（Gi，Vi）和e（Hi，Vi）值，這樣在簽名和驗(yàn)證時(shí)就省去了此配對(duì)計(jì)算的工作量，而只需要2（k－1）次普通點(diǎn)乘即可（k是簽名時(shí)所選環(huán)的大小）。

（3）Sign：設(shè)待簽名消息為m，成員i先計(jì)算δi（m）＝g1／（H（m）＋si），H 是一哈希函 數(shù)，再 從環(huán)中隨 機(jī) 選 一子集 R（包含其自身），計(jì)算：令然后用Groth－Sahai證明系統(tǒng)證明：

PK｛（Wg，Wh，Gi，Hi，Vi，δ）：e（g，Wg）e（Gi，Vi）＝Cg∧e（h，Wh）e（Hi，Vi）＝ Ch∧ Gi是 G1…Gn之 一 ∧ Hi是H1…Hn之一 ∧e（δ，gH（M）Vi）＝e（g，g）｝

其中實(shí)現(xiàn)Gi是G1，…，Gn之一的技巧是證明其知道Gi的SPS簽名 （類似證明Hi），上面的方程以及SPS簽名的驗(yàn)證方程都是PPE方程，因而存在Groth－Sahai證明；

（5）Open：握有Groth－Sahai證明系統(tǒng) “證據(jù)”提取密鑰的RM可從一合法的環(huán)簽名中提取出承諾值中的成員公鑰Vi，從而找出真正的簽名者。

4 安全性

環(huán)簽名安全性一般包括兩個(gè)方面：匿名性與不可偽造性，下面來證明我們的方案滿足這兩種安全特性：

定理1 基于DLIN假設(shè)，上述環(huán)簽名方案滿足匿名性。

證明：上述環(huán)簽名主要是一NIZK證明，公開的是R，Cg，Ch不包含特定簽名者的信息，而包含簽名者的信息如Vi，Gi，Wg，Whδ等都以 “承諾值”的形式給出，因而是匿名的，相關(guān)的證明元素由Groth－Sahai證明系統(tǒng)的安全性（基于DLIN）也不會(huì)透露簽名者的信息，所以我們的方案是匿名的。

定理2 基于DLIN、SDH假設(shè)，上述環(huán)簽名方案滿足不可偽造性。

證明：由上述環(huán)簽名的構(gòu)造可見，在Groth－Sahai證明系統(tǒng)安全的前提下，要偽造簽名可分為兩種情況：一是用真正的證據(jù)Wi，而偽造簽名δ；二是偽造V，Wh，Wg使得但有e（Hi，V）e（h，Wh）＝Ch和e（Gi，V）e（g，Wg）＝Cg，下面來證明這兩種情況都是不可行的：

Case1：Wi用真的，此時(shí)要根據(jù)公鑰Vi來偽造Boneh－Boyen簽名δ，而根據(jù)BB簽名的安全性 （基于SDH假設(shè)），這是計(jì)算上不可行的；

Case2：偽造Vfake使得Vfake不是R中的一個(gè)公鑰，但有 e（G1，Vfake）e（g，）＝ Cg＝ e（G1，V1）e（g，）和e（H1，Vfake）e（h，）＝ Ch＝e（H1，V1）e（h，），其 中V1是R中第一個(gè)成員的公鑰，下面我們來證明基于DLIN假設(shè)，這是不可行的；假設(shè)存在A能找到這樣的V與Wh，Wg，我們顯示如何用A來解決SDP難題，而解決SDP難題就意味著解決DLIN（因SDP是有DLIN所蘊(yùn)含的）難題。

給定SDP問題 （gz，gr，hz，hu）∈G，要找到 （z，r，u）∈G 滿足e（gz，z）·e（gr，r）＝1且e（hz，z）·e（hu，u）＝1；在上述環(huán)簽名方案中令G1＝gz，H1＝hz，g＝gr，h＝hu，利用A可找到滿足和顯 然 令是原SDP問題的解。

5 性能比較

在表1中我們比較了本文方案與現(xiàn)有的標(biāo)準(zhǔn)模型下的環(huán)簽名方案的效率。

表1中k表示的是簽名時(shí)環(huán)的大小，n表示所支持環(huán)成員的最大數(shù)目。因?yàn)樵诜治龊灻?yàn)證復(fù)雜度時(shí)，通常只考慮比較耗時(shí)的配對(duì)運(yùn)算與指數(shù)運(yùn)算［4］，而群中的點(diǎn)乘運(yùn)算由于耗時(shí)較少經(jīng)常被忽略，而本文方案簽名／驗(yàn)證計(jì)算中與環(huán)大小k相關(guān)的運(yùn)算是和 Wg＝等，都是點(diǎn)乘運(yùn)算，其它的運(yùn)算如配對(duì)、指數(shù)運(yùn)算都是常數(shù)級(jí)別O（1）的，因而我們稱其復(fù)雜度為 “Almost O（1）”。

表1中的前3個(gè)方案是基于身份的環(huán)簽名方案，第4個(gè)不是基于身份的。顯然從表1可見本文方案的效率要優(yōu)于現(xiàn)有的標(biāo)準(zhǔn)模型下安全的環(huán)簽名方案 （包括基于或不基于身份的方案），尤其是當(dāng)環(huán)的大小k很大時(shí)，優(yōu)勢(shì)更加明顯，也即本文方案更適合環(huán)成員數(shù)目很多的場(chǎng)合。

表1 本文方案與現(xiàn)有標(biāo)準(zhǔn)模型下的環(huán)簽名方案的效率比較

6 結(jié)束語

本文基于SPS與Groth－Sahai證明系統(tǒng)，提出了一種新的匿名性可撤銷環(huán)簽名構(gòu)建方法，同以往的環(huán)簽名方案相比，一個(gè)不同是增加了一個(gè)環(huán)簽名員，且用戶成為環(huán)成員之前有一個(gè)加入過程，解決了基于身份的環(huán)簽名中的 “密鑰托管”問題，此外其效率較高，簽名大小為常數(shù)，且其安全性不依賴與ROM，而是基于標(biāo)準(zhǔn)模型的；且匿名性在必要是可由RM來撤銷。未來可能的一個(gè)研究方向是如何提高效率，尤其是雖然我們方案的簽名大小為常數(shù)，但具體數(shù)值較大 （由于采用的SPS簽名的大小較大），可進(jìn)一步研究如何減小此具體數(shù)值。

［1］WANG Huaqun，JIANG Guoxing，ZHAO Shuping.Efficient ring signature scheme from bilinear pairings ［J］.Computer Engineering and Design，2008，29 （6）：1459－1461 （in Chinese）.［王化群，姜國興，趙樹平.高效的基于雙線性對(duì)的環(huán)簽 名 方 案 ［J］. 計(jì) 算 機(jī) 工 程 與 設(shè) 計(jì)，2008，29 （6）：1459－1461.］

［2］Nishanth Chandran，Jens Groth，Amit Sahai.Ring signatures of sub－linear size without random oracles ［G］.LNCS 4596：Automata，Languages and Programming，2007：423－434.

［3］YU Ting，ZHAO Zemao，REN Xifeng.Efficient identitybased ring signature in standard model ［J］.Journal of Compu－ter Applications，2012，32 （7）：2015－2017 （in Chinese）.［余婷，趙澤茂，任錫灃.標(biāo)準(zhǔn)模型下基于身份的高效環(huán)簽名［J］.計(jì)算機(jī)應(yīng)用，2012，32 （7）：2015－2017.］

［4］GE Aijun，MA Chuangui，ZHANG Zhenfeng，et al.Identitybased ring signature scheme with constant size signatures in the standard model［J］.Chinese Journal of Computers，2012，35（9）：1874－1880 （in Chinese）. ［葛愛軍，馬傳貴，張振峰，等.標(biāo)準(zhǔn)模型下固定長度的基于身份環(huán)簽名方案 ［J］.計(jì)算機(jī)學(xué)報(bào)，2012，35 （9）：1874－1880.］

［5］LIU Zhenhua，HU Yupu，MU Ningbo，et al.New identitybased ring signature in the standard model ［J］.Journal of Electronics ＆Information Technology，2009，31 （7）：1727－1731（in Chinese）.［劉振華，胡予濮，牟寧波，等.新的標(biāo)準(zhǔn)模型下基于身份環(huán)簽名方案 ［J］.電子與信息學(xué)報(bào)，2009，31 （7）：1727－1731.］

［6］ZHANG Mingwu，YANG Bo，YAO Jintao，et al.Cryptanalysis and design of signature schemes with identity ambiguity in the standard model ［J］.Journal of Communications，2011，32 （5）：40－46 （in Chinese）. ［張明武，楊波，姚金濤，等.標(biāo)準(zhǔn)模型下身份匿名簽名方案分析與設(shè)計(jì) ［J］.通信學(xué)報(bào)，2011，32 （5）：40－46.］

［7］WANG Huaqun，QIN Bo.Cryptanalysis and improvements of some ring signature and its extended signature schemes ［J］.Chinese Journal of Computers，2012，35 （5）：1052－1058 （in Chinese）.［王化群，秦波.一些環(huán)簽名及其擴(kuò)展簽名方案的安全 性 分 析 及 改 進(jìn) ［J］.計(jì) 算 機(jī) 學(xué) 報(bào)，2012，35 （5）：1052－1058.］

［8］ WANG Fenghe，HU Yupu，WANG Chunxiao.A latticebased ring signature scheme from bonsai trees ［J］.Journal of Electronics ＆Information Technology，2010，32 （10）：2400－2403（in Chinese）.［王鳳和，胡予濮，王春曉.格上基于盆景樹模型的環(huán)簽名 ［J］.電子與信息學(xué)報(bào)，2010，32 （10）：2400－2403.］

［9］TIAN Miaomaio，HUANG Liusheng，YANG Wei.Efficient lattice－based ring signature scheme ［J］.Chinese Journal of Computers，2012，35 （4）：712－718 （in Chinese）. ［田苗苗，黃劉生，楊威.高效的基于格的環(huán)簽名方案 ［J］.計(jì)算機(jī)學(xué)報(bào)，2012，35 （4）：712－718.］

［10］Masayuki Abe，Melissa Chase，Bernardo David，et al.Constant－size structure－preserving signatures：Generic constructions and simple assumptions ［G］.LNCS 7658：Advances in Cryptology，2012：4－24.

［11］Jens Groth，Amit Sahai.Efficient non－interactive proof systems for bilinear groups ［G］.LNCS 4965：Advances in Cryptology：2008：415－432.

［12］HUANG Dawei，YANG Xiaoyuan，CHEN Haibin.Ring signature scheme with revocable anonymity ［J］.Computer Engineering and Applications，2010，46 （24）：88－89 （in Chinese）. ［黃大威，楊曉元，陳海濱.一種可撤銷匿名性的環(huán)簽名方案 ［J］.計(jì)算機(jī)工程與應(yīng)用，2010，46 （24）：88－89.］

［13］Julien Cathalo，Benoit Libert，Moti Yung.Group encryption：Non－interactive realization in the standard model ［G］.LNCS 5912：Advances in Cryptology，2009：179－196.

［14］Jens Groth.Fully anonymous group signatures without ran－dom oracles ［G］.LNCS 4833：Advances in Cryptology，2007：164－180.