基于混沌果蠅算法的WSN優化布局
徐躍州,張 欣
(貴州大學 大數據與信息工程學院,貴州 貴陽550025)
0 引 言
無線傳感器網絡[1]節點的優化部署研究可以有效提高傳感器網絡覆蓋率和降低能耗,增長網絡壽命。目前,常用的優化算法有虛擬力算法 (VFA)、螢火蟲群優化(GSO)、粒子群算法 (PSO)、蛙跳算法 (SFLA)等,文獻 [2-5]分別采用VFA、GSO、PSO、SFLA這4種算法對傳感器網絡節點進行優化部署,提升監測區域的覆蓋率。然而,上述算法卻存在著高復雜度、低收斂速度和精度等問題。針對這些問題,本文提出一種簡單、高效的混沌果蠅算法 (chaotic fruit fly algorithm,CFOA),并通過仿真驗證分析其性能的優越性。
1 果蠅算法
果蠅 算 法[6](fruit fly optimization algorithm,FOA)是2011年臺灣學者潘文超從果蠅覓食行為中得到啟發,提出的一種尋求全局優化的新方法,是一種新型仿生行為學智能算法,廣泛運用于求解函數極值、Z-SCORE模型的系數調整、向量機參數優化以及各類廣義回歸神經網絡系數優化等[7]。由于算法提出較晚,FOA的研究仍處于起步階段,理論尚不成熟,如對多維極值復雜優化的問題等。
FOA與VFA、GSO、PSO、SFLA相比,不但算法簡單、收斂速度快 (如SFLA和PSO的優化方程為二階微分方程,而FOA的優化方程為一階微分方程)、代碼運行時間短,且FOA僅需調整3個參數,算法復雜度低;而其它仿生算法至少需調整6、7個參數,各個參數間的關系和相互影響十分復雜,導致分析算法的復雜度變得異常困難[8]。與此同時,果蠅算法和上述算法一樣,極易陷入局部最優解,以至于后期收斂精度降低、收斂速度變慢,特別是對于高維多極值復雜優化問題。
2 混沌優化
混沌優化 (chaos optimization,CP)是利用混沌運動的隨機性、遍歷性、規律性和初值敏感性來提高隨機優化算法的效率[9],混沌運動介于確定性與隨機性之間,具有豐富的時空動態,并且混沌搜索能在一定范圍內按其身的“規律性”不重復的遍歷所有狀態。Logistic映射系統是混沌系統中最著名的系統模型之一,其模型如下
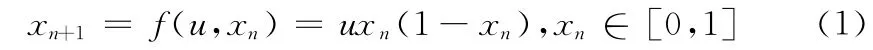
當u=4時,系統處于混沌狀態。若xi∈[mi,ni],可由式 (2)、式 (3)對混沌變量xi進行往返映射,具體的混沌搜索迭代方法可見文獻 [10]
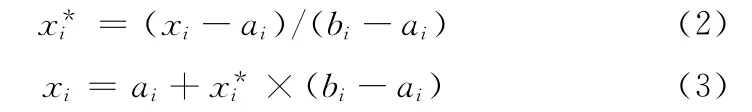
由于果蠅算法類似于其它智能算法,均為通過對初值的迭代和進化尋求最優解,初值的選取不當極易使算法陷入局部最優,而對于傳感器網絡節點部署,模型及其復雜,很難找出一個對初值的評價標準。為了避免算法陷入局部最優,采用混沌優化,隨機生成一個混沌擾動因子,在每次果蠅群進化前進行混沌擾動,使果蠅群迅速跳出局部尋優,進行全局搜索。
3 WSN節點部署模型
假設在一個二維監測區域,區域被離散化為m*n個像素點,每個像素點表示為(m,n)。在該區域內投入N個傳感器節點,其感知半徑為r。傳感器的節點集表示為式(4),節點和像素點距離為式 (5)
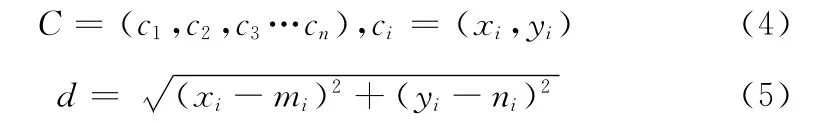
則像素點(mi,ni)被節點ci監測到的概率為
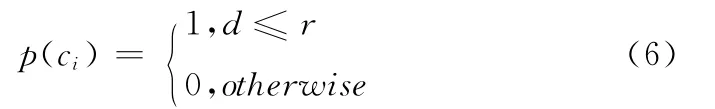
所以,該像素點被節點集C聯合監測到的概率為
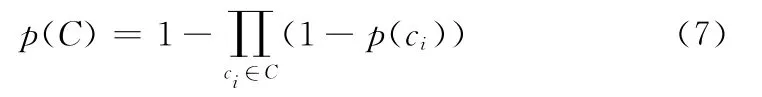
綜上,傳感器網絡的節點覆蓋率[11]為
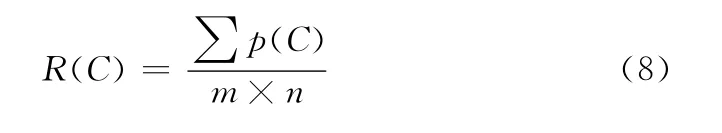
4 混沌果蠅算法的應用和性能分析
本文在借鑒文獻 [12]的基礎上,提出混沌果蠅算法,具體算法如下:
步驟1 隨機初始化N個果蠅位置,Smellbest=0,步長h;果蠅位置為: (Init X(i),Init Y(i)),其中i∈(1,N);
步驟2 根據式 (8)、式 (9),求出覆蓋率最大的果蠅及其位置
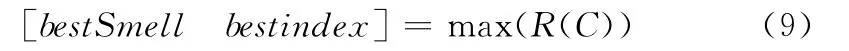
步驟3 記錄果蠅位置和覆蓋率,所有果蠅飛向該位置,如式 (10)所示

步驟4 根據果蠅步長h,每個果蠅隨機向4周搜尋食物,如式 (11),其中K為節點個數
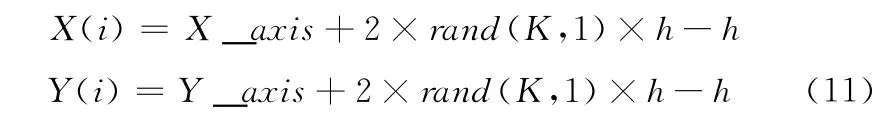
步驟5 重復步驟2;
步驟6 對當前覆蓋率最大的果蠅進行混沌搜索,隨機生成兩個n維變量
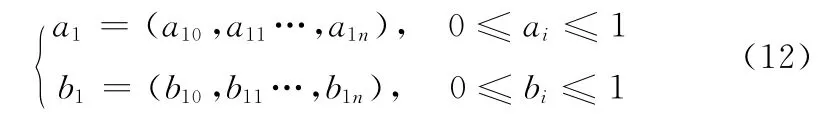
根據混沌模型可得式 (13),將得到的 (a2,b2)各個分量載波到混沌擾動范圍[-d,d],則擾動量為式 (14),此時新位置坐標為式 (15)
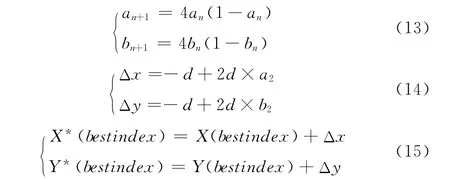
計算新老位置的覆蓋率f*、f,若f*>f,則
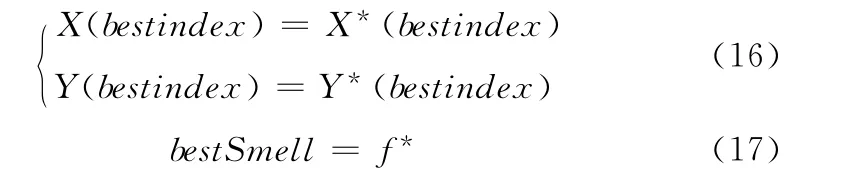
若f*<f,則果蠅位置與bestSmell不變,混沌搜索迭代M次。
步驟7 重復步驟3。
步驟8 迭代步驟4~步驟7,直至迭代結束,得到最優分簇 (X_axis,Y_axis)和最優解Smellbest。
從上述算法流程可以看出,CFOA每次迭代時,所有果蠅均聚集到當前最優位置進行尋優,相對于其它智能算法各個因子從當前位置移動向最優位置尋優,具有更好的收斂速度;對于智能算法 “早熟”問題,CFOA每次迭代時,對當前的最優位置進行混沌擾動,及時跳出 “早熟收斂”,進行全局尋優。顯然,混沌果蠅算法具有更高的收斂速度和收斂精度。
5 仿真結果及分析
假定在邊長為50 m的正方形監測區域中放置25個同一性能的傳感器網絡節點,節點額監測半徑r=5 m。當粒子數為待測區域面積的0.25%至4%時,偏差約為0.1%至0.5%,綜合分析,本文均勻選取2500個粒子,使實驗結果具有較小的偏差性。為了分析CFOA中果蠅算法的參數選擇,本文從不同果蠅種群,不同初始覆蓋率以及不同迭代步長3個方面進行仿真研究,挑選出合適的參數應用于混沌果蠅算法,如圖1~圖3所示。所有算法均在MATLAB2012上進行仿真模擬。

圖1 種群數目不同的網絡覆蓋率

圖2 初始覆蓋率不同的網絡覆蓋率
如圖1所示,選取固定的果蠅群 (初始覆蓋率為58.3%),步長h=1,迭代200次。從圖1中可以看出數量大的果蠅群 ((N=100))在算法前期體現出良好的收斂性和收斂精度,但隨著算法迭代,數量小的果蠅群 (N=50)和數量大的果蠅群在收斂精度上漸漸趨于一致。
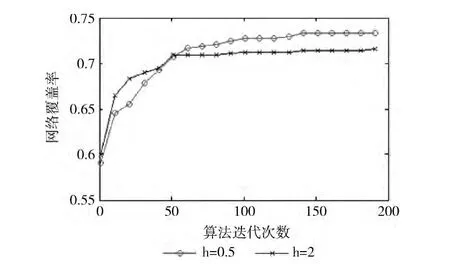
圖3 步長不同的網絡覆蓋率
如圖2所示,選取不同的果蠅群 (初始覆蓋率為59%、63%),步長h=1,迭代200次,果蠅種群數量N=50。從圖2中可看出初始覆蓋率為63%的果蠅算法全局收斂性和收斂精度均遠高于初始覆蓋率為59%的果蠅算法。這表明果蠅算法的初始布局直接影響傳感器網絡最終布局的優劣。
如圖3所示,選取固定的果蠅群,相同的迭代次數,不同的步長h。從圖3中可以看出,步長為兩個單位的果蠅群在前期收斂速度很快,但后期步長小的果蠅群收斂速度和精度卻漸漸超過步長大的果蠅群。這說明選擇合適果蠅步長將直接提升算法的性能。
如圖4~圖7所示,選取近些年深入研究的蛙跳和虛擬力算法與混沌果蠅算法作比較,蛙跳算法參數為:種群分組數m=8,模因組青蛙數n=8,組內最大迭代數Ne=8;虛擬力算法參數為:距離閾值dth=10 m,Max_Step=2.5 m;混沌果蠅算法參數為:N=100,h=1,M=50。圖4~圖7是4種算法的節點覆蓋圖,在邊長為50m的正方形監測區域,25個傳感器節點理論最優覆蓋率為78.5%。圖4為蛙跳算法200輪后節點覆蓋圖,占62.5%,達到最優覆蓋率的79.6%;圖5為虛擬力算法200輪后節點覆蓋圖,占67.3%,達到最優覆蓋率的85.7%;圖6為果蠅算法200輪后覆蓋圖,占72.7%,達到最優覆蓋率的92.6%;圖7為混沌果蠅算法200輪后覆蓋圖,占76.4%,達到最優覆蓋率的97.3%。仿真結果表明,果蠅算法和改進果蠅算法要明顯優于蛙跳和虛擬力算法,改進果蠅算法更易于擺脫局部極值解,尋求全局最優解。
如圖8所示,混沌果蠅算法和果蠅算法在收斂速度和收斂精度上遠優于虛擬力算法和蛙跳算法,更適用于WSN節點布局優化。果蠅算法在前期性能較好,但在后期隨著網絡布局的穩定漸漸收斂,陷于局部極值解;而混沌果蠅算法能夠在果蠅進化時進行混沌擾動,跳出局部搜索,進行全局尋優,具有更好的網絡布局優化性能。
6 結束語
本文針對WSN傳統算法覆蓋率低、算法復雜高的問題,提出一種簡單、高效的混沌果蠅算法,并應用于無線傳感器網絡的節點布局。該算法通過在果蠅算法每次進化時對當前最優解進行混沌擾動,保證果蠅群在下輪迭代時具有一個更好的初始值。
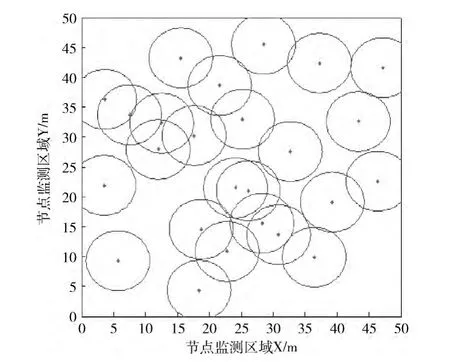
圖4 蛙跳算法節點覆蓋
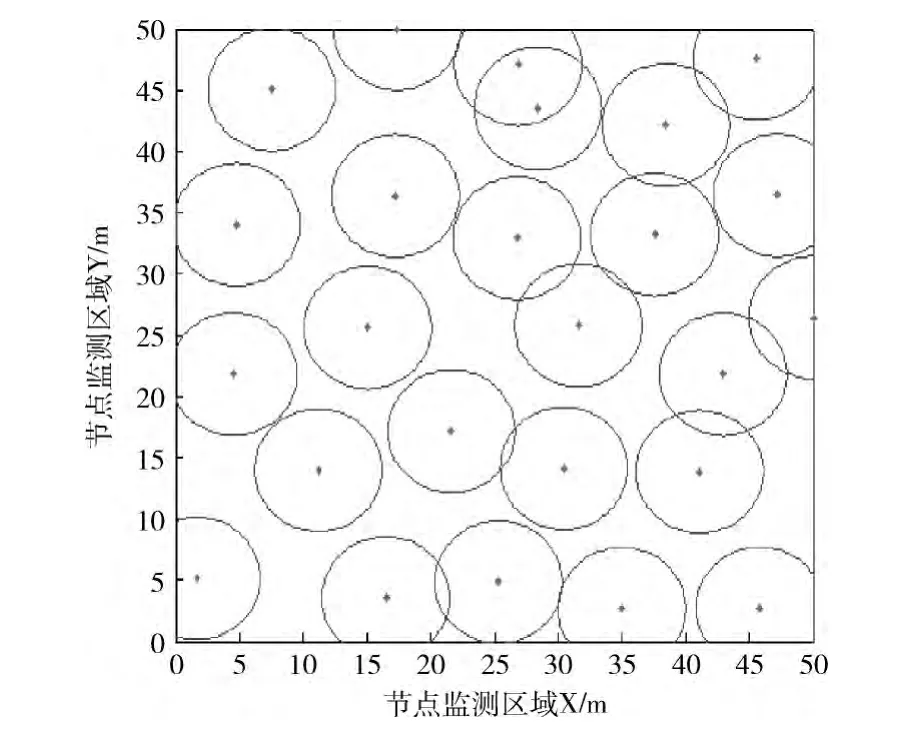
圖5 虛擬力算法節點覆蓋
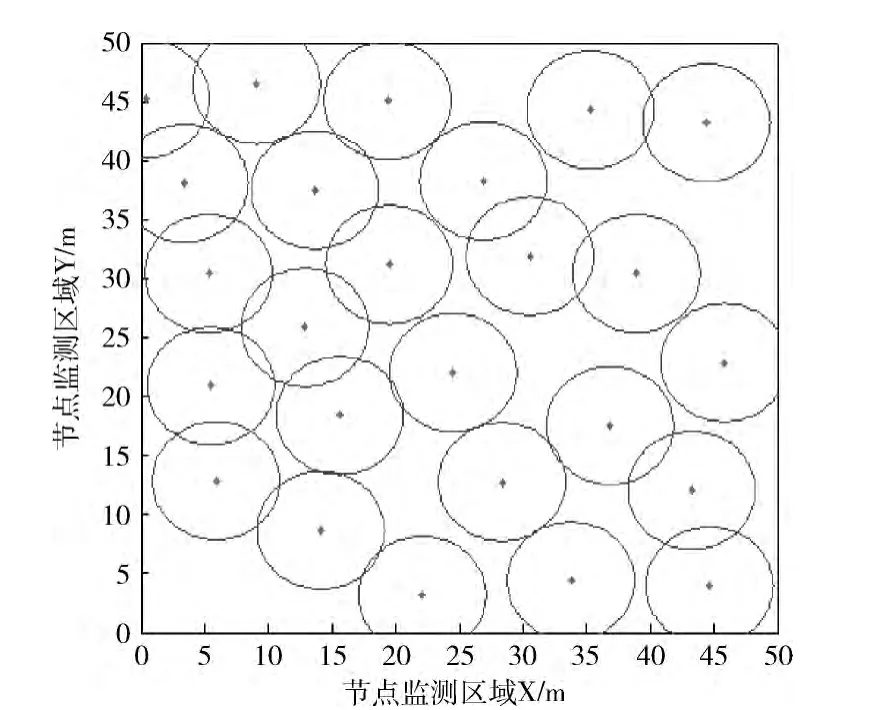
圖6 果蠅算法節點覆蓋
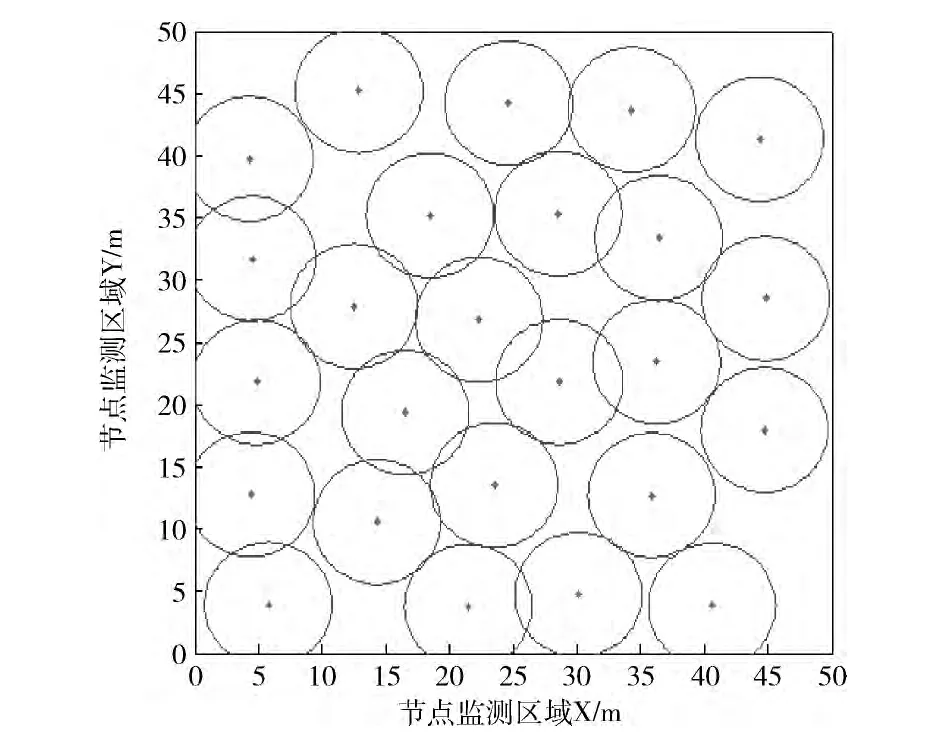
圖7 混沌果蠅算法節點覆蓋
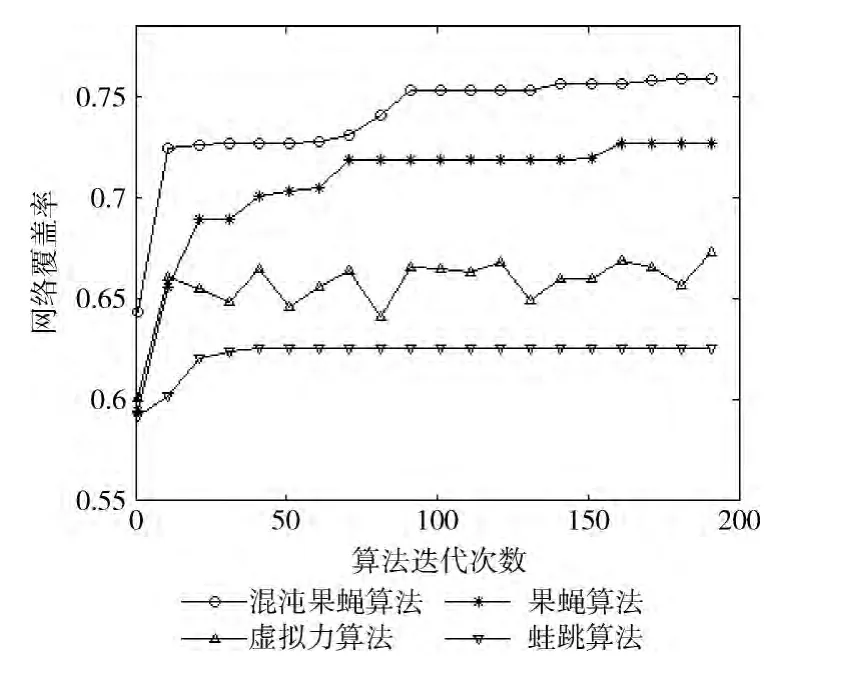
圖8 4種算法性能比較
通過MATLAB仿真結果表明,混沌果蠅算法能夠迅速跳出局部極值解,進行全局搜索。相對于其它智能算法,混沌果蠅算法具有更高的網絡覆蓋率、更快的收斂速度以及更低的算法復雜度,更適應于當前的傳感器網絡布局優化。隨著WSN發展迅速,應用廣泛,下一步將重點研究傳感器節點基于混沌果蠅算法的動態半徑規劃。
[1]WANG Chengliang,WANG Qiang.Activity-aware &energy balance based routing protocol for wireless sensor networks[J].Journal of Beijing University of Aeronautics and Astronautics,2014,40 (1):10-17 (in Chinese).[汪成亮,王強.基于活動預測和能耗均衡的WSN路由算法 [J].北京航空航天大學學報.2014,40 (1):10-17.]
[2]LI Qiangyi,MA Dongqian,ZHANG Juwei.Nodes deployment algorithm based on perceived probability of wireless sensor network [J].Computer Measurement & Control,2014,22(2):643-645 (in Chinese). [李強懿,馬冬前,張聚偉.基于感知概率的無線傳感器網絡節點部署算法 [J].計算機測量與控制,2014,22 (2):643-645.]
[3]LIU Cuiping,ZHANG Haitao,BAI Ge.Node deployment of wireless sensor network based on glowworm swarm optimization algorithm [J].Journal of Computer Applications,2013,33(4):905-907 (in Chinese). [劉翠蘋,張海濤,白舸.基于螢火蟲群優化算法的無線傳感器節點部署 [J].計算機應用,2013,33 (4):905-907.]
[4]SONG Mingzhi,YANG Le.Improving coverage of wireless sensor network using enhanced adaptive PSO algorithm [J].Application Research of Computers,2013,30 (11):3472-3475(in Chinese).[宋明智,楊樂.基于改進自適應PSO算法的WSN覆蓋優化方法 [J].計算機應用研究,2013,30(11):3472-3475.]
[5]LONG Teng,SUN Hui,ZHAO Jia.Research of mobile node deployment in WSN based on improved frog leaping algorithm[J].Computer Engineering,2012,38 (5):96-98 (in Chinese).[龍騰,孫輝,趙嘉.基于改進蛙跳算法的 WSN移動節點部署研究 [J].計算機工程,2012,38 (5):96-98.]
[6]PAN Wenchao.Using fruit fly optimization algorithm optimized general regression neural network to construct the operating performance of enterprises model [J].Journal of Taiyuan University of Technology,2011,29 (4):1-5 (in Chinese). [潘文超.應用果蠅優化算法優化廣義回歸神經網絡進行企業經營績效評估 [J].太原理工大學學報,2011,29 (4):1-5.]
[7]CHENG Hui,LIU Chengzhong.Mixed fruit fly optimization algorithm based on chaotic mapping [J].Computer Enginee-ring,2013,39 (5):218-221 (in Chinese). [程慧,劉成忠.基于混沌映射的混合果蠅優化算法 [J].計算機工程,2013,39 (5):218-221.]
[8]HAN Junying,LIU Chengzhong.Fruit fly optimization algorithm with adaptive mutation [J].Application Research of Computers,2013,30 (9):2641-2644 (in Chinese). [韓俊英,劉成忠.自適應變異的果蠅優化算法 [J].計算機應用研究,2013,30 (9):2641-2644.]
[9]LIU Changping,YE Chunming.Firefly algorithm with chaotic search strategy [J].Journal of Systems & Management,2013,22 (4):538-543 (in Chinese). [劉長平,葉春明.具有混沌搜索策略的螢火蟲優化算法 [J].系統管理學報,2013,22 (4):538-543.]
[10]ZHAN Mengmeng.Reactive power optimization of distribution network based on modified chaos genetic algorithm [D].Hangzhou:Hangzhou Dianzi University,2013:19-21 (in Chinese).[詹萌萌.基于改進混沌遺傳算法的配電網無功優化 [D].杭州:杭州電子科技大學,2013:19-21.]
[11]LI Li.Strategy of WSN coverage optimization by improved artificial fish swarm algorithm [J].Microelectronics & Computer,2013,30 (2):83-86 (in Chinese). [李麗.基于改進魚群算法的WSN覆蓋優化策略 [J].微電子學與計算機,2013,30 (2):83-86.]
[12]PAN Wenchao.A new fruit fly optimization algorithm:Taking the financial distress model as an example [J].Knowledge-Based Systems,2012,26:69-74.

