基于稀疏正則化結合NLS的超分辨率圖像重建

王華君，孟德建，姚 湘

(無錫太湖學院 工學院，江蘇 無錫 214064)

基于稀疏正則化結合NLS的超分辨率圖像重建

王華君，孟德建，姚 湘

(無錫太湖學院 工學院，江蘇 無錫 214064)

為了保持高光譜(HS)超分辨率重建過程中的頻譜一致性和邊緣銳度，提出一種基于空間譜結合非局部相似性的超分辨率重建算法。首先，使用HS圖像生成模型，采用稀疏正則化解決全色(PAN)圖像和HS圖像重建的病態問題求逆；然后分析了從高空間分辨率到低空間分辨率數據生成的豐度系數映射；最后利用非局部相似性，設計空間譜聯合正則化項。使用機載可見光/紅外成像光譜儀(AVIRIS)和Hyperion圖像測試該算法，實驗結果表明，提出的算法重建圖像在PSNR，SSIM和FSIM方面明顯高于其他優秀算法，在SAM和ERGAS方面明顯低于其他優秀算法，在光譜失真方面丟失最少，僅有2%～3%，低于其他算法30%左右，且重建效果更加清晰自然。

高光譜；超分辨率重建；非局部相似性；稀疏正則化；全色圖像

最近幾十年，高光譜(hyperspectral， HS)[1-2]成像的理論和技術發展非常迅速，應用極其廣泛，如地形分類、礦物檢測和勘探、遙感制圖、環境監測，以及軍事監視等[3]。由于儀器限制和不完美成像光學器件，HS傳感器譜相元分辨率很高，但對應的物分辨率卻很有限，HS圖像難以獲取高分辨率數據，大大降低了民用和軍事領域所需的檢測和識別性能[4]。因此，如何提高HS數據空間分辨率成為一項重要課題。

文獻[5]以最大后驗概率(Maximum Posterior Probability， MAP)為理論基礎，利用感興趣類別端元將原始高維數據映射到低維空間，以MAP為理論基礎，給出HS圖像重建的MAP模型。文獻[6]結合局部和非局部相似性約束，同場景的高分辨率場景彩色圖像的自適應權重濾波，在頻譜一致性方面表現并不好。高分辨率圖像像素空間位置可以從HR PAN圖像獲得或從相應的HR HS圖像了解到。文獻[7]提出一種基于混合信息和總變差(Total Variation， TV)最小化來產生HR HS圖像的算法，但TV正則化會導致圖像邊緣紋理細節的模糊和丟失。文獻[8-9]提出了其他基于軟分類輸出的超分辨率映射算法，進一步改善了重合圖像的質量，然而，其重構結果依賴于分類的準確性。

為了獲得更好的重建效果，本文提出了一種基于非局部相似結合稀疏正則化的HS圖像超分辨率算法，在超分辨率過程中合并了分離結果和PAN信息，通過從PAN圖像中提取類似的小塊來預測HS圖像中的小塊，即所預期的表示誤差很小，這與稀疏表達的超分辨率思想[10-11]很像。將稀疏正則化和非局部相似性(Non-Local Similarity， NLS)有效結合，有助于保留邊緣清晰度和頻譜一致性，且可以很好地抑制噪聲。

1 非局部相似性和稀疏融合

HS超分辨率問題是一種典型的病態問題求逆，由于LR圖像數量不足，在超分辨率重建算法中，解決方案不唯一，正則化算法是進一步穩定病態問題求逆[12]的有效算法。

1.1 空間譜聯合非局部結構相似

HS圖像采集過程可以參照文獻[12]建模

Y=WHX+v

(1)

式中:Y表示LR HS數據；X表示HR HS數據；W表示空間譜下采樣算子；H表示模糊濾波器引起的空間譜，例如大氣湍流；v是加性噪聲。

X可以通過式(2)來估算

(2)

這是極為病態的，因為對于給定的輸入Y，無限多的圖像X可能滿足上述重建約束。由于在觀察的場景中有許多非局部重復物質，它們具有相似的光譜和空間結構，利用非局部重復可以提高圖像重建的質量。受到非局部均值濾波成功用于圖像去噪和檢索的啟發，引入了非局部自相似超分辨率過程，以充分利用重復，利用從HR和LR HS數據生成的豐度映射系數中的非局部相似引入空間譜聯合結構相似。

HR HS數據光譜混合模型[12]可表示為

(3)

假定端元在空間分辨率增強后不變化，當式(1)中HR數據X和LR數據Y表示相同場景時，相應的端元應該相同。基于式(1)中的HS數據模型，LR數據Y可由下采樣和空間模糊濾波器獲得，該LR HS光譜混合模型可表示為

(4)

對于每一個局部小塊Yi，基于端元比例相似在整個圖像Y尋找相似小塊，小塊Yji可以選擇作為Yi的一個相似小塊，如果

(5)

(6)

(7)

(8)

I是單位矩陣，B設置如下

通過基于式(2)結合非局部結構相似性光譜和空間域到超分辨率恢復過程，得到下列基于空間譜聯合非局部結構相似性的HS超分辨率問題

(9)

1.2 HS和PAN圖像稀疏融合

HS和PAN圖像融合的目的是通過整合具有不同空間和光譜分辨率數據所傳遞信息，各種圖像融合技術利用互補空間/頻譜分辨率特性來產生HR HS觀察[7]。使用Y表示LR HS數據，使用P表示HR PAN圖像，融合過程可表示為

Z=f(T1(Y),T2(P))

(10)

式中，f是融合規則，T1和T2代表相應的變換，傳統上，T1和T2可以是小波變換、曲波變換或一些其他多尺度技術，通過預定義的融合規則， PAN的空間結構注入到HS數據。但是這些算法都無法避免光譜失真。作為一種強大的統計圖像建模技術，稀疏編碼可以利用訓練過的字典原子項表示結構信息。

根據文獻[2]提出的HS稀疏融合模型和稀疏表示模型，HR圖像X可估計為

(11)

作為一種稀疏融合技術，文獻[13]設計了線性退化模型，涉及HR圖像到LR MS圖像和PAN HR圖像，降解過程可視為壓縮傳感，l1-范式用作融合MS和PAN圖像的正則項，頻譜一致性由PAN圖像通過MS圖像的線性組合近似的假設來保證。僅有彩色圖像的情況下，獲得HS和PAN數據的組合權重很困難，此時很難獲得滿意的恢復結果。

1.3 超分辨率重建

空間譜聯合非局部HS超分辨處理僅基于低空間HS圖像，雖然這種算法能保持光譜的一致性，但是在超分辨率過程中無額外信息引入。稀疏正則化過程將保留邊緣銳度，式(11)表示HS和PAN圖像融合過程，通過引入PAN信息，邊緣銳度保留，除去空間域中噪聲。式(9)表示基于空間譜聯合非局部結構相似性的超分辨率，這種重建算法提供了良好的光譜一致性。通過組合式(9)和式(11)，PAN圖像信息集成到非局部HS超分辨率處理中，得到最終的超分辨率重建問題

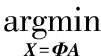
(12)

為了求解式(12)，引入一個臨時變量V，假設V≈X，則可以得到

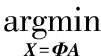
(13)

超分辨率算法如算法1所示。

算法1：基于空間譜聯合非局部相似的HS超分辨率算法

輸入：LR HR圖像Y，由與Y不相關的HR PAN訓練過的字典Φ

使用非局部權重初始化B，使用Y的下采樣初始化X

初始化μ,λ,η,γ

Loops begin：

相對于A的優化

相對于V的優化

相對于X的優化

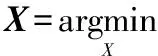
Loops end

停止準則可設計為固定迭代次數、運行時間、第T次迭代和第T-1次迭代之間的誤差。

2 實驗

將本文算法與4種優秀算法進行比較，包括：基于光譜調節的算法[2](SRSR)、基于改進的MAP HS圖像超分辨率算法[5](MMAP)、端元TV-正則化算法[7](ETV)和基于稀疏塊分類表示的算法[11](SRCIP)。第一個實驗，PAN圖像光譜范圍覆蓋HS數據的跨度，第二個實驗中，PAN圖像的光譜范圍不覆蓋HS數據的整個跨度。使用5種量化指標，即峰值信噪比(PSNR)、結構相似性(SSIM)指標、功能相似性(FSIM)指標[2]、光譜角映射(SAM)和相對全局合成維度誤差(ERGAS)。

2.1 評估指標

評估空間分辨率增強性能的最常用指標是PSNR，每個頻帶信號峰值可以顯著改變，這使得該指標偏向具有更高能量的頻帶，第b個頻帶的PSNR定義為

(14)

式中:Speak,b第b個頻帶信號峰值;MSEb為地面實況與估計的第b個頻帶之間均方差。

(15)

式中：M和N表示超分辨圖像中行和列的數目；ISR,b為所估計的分辨率增強圖像；Io,b為原始HR圖像。

PSNR可以用來評估重建質量，結構信息用于表示具有較強相互依賴的像素在空間上接近，這些依賴關系攜帶關于場景中對象結構的重要信息。2幅普通大小為N×NHS圖像x和y之間的量度為

(16)

式中：μx是x的平均值；μy是y的平均值；vx是x的方差；vy是y的方差；vxy是vx和vy的協方差；C1=(k1L)2和C2=(k2L)2是2個變量，用于穩定具有弱分母的除法；L為像素值的動態范圍，默認k1=0.01，k1=0.03。

文獻[14]提出了一種新的FSIM指標，用于完整參考圖像的質量評估，在評估過程中同時使用相位一致性(PC)和梯度幅度(GM)，HS圖像x和y之間的FSIM指標可定義為

(17)

式中:Ω意味著整個圖像空間域，PCm(z)=max{PCx(z),PCy(z)}，其中PCx(z)是對于圖像x給定位置z的相位一致性，SL(z)為對于給定位置z的GM。

SAM通過從源圖像y和增強圖像x每個像素構建的2個向量之間的絕對角度來影響光譜失真。令μx和μy分別表示x和y像素的頻譜向量，HS圖像x和y之間的SAM由下式計算

(18)

ERGAS指標可用來量化不同超分辨率結果的光譜和空間質量，該指標定義為

(19)

式中:α為放大倍數;P為光譜帶的數量;MHSi為每個頻帶的平均。對于完全增強的圖像，ERGAS也應該是零。

2.2 AVIRIS數據集

AVIRIS數據集中的HS圖像由AVIRIS傳感器收集，在370～2 510 nm范圍內有224個光譜帶、400×400像素和 3.5 μm 空間分辨率。圖像使用ENVI的FLASH模塊常壓校正，產生反射率圖像，除去噪聲頻帶后，共有189條頻帶保留。在這個場景中，有人造對象(道路、屋頂、和飛機)、草地、樹木，人造對象有鋒利的邊緣，而草地和樹木有豐富的質感。在實驗中，首先對原始圖像在1.6標準偏差下運用截短的7×7高斯內核，然后由因子為3的均值濾波器進行下采樣，產生退化的LR PAN和HS圖像。式(13)中，λ和η是自由參數，λ用于調整l1-范式的貢獻，η用于平衡非局部正則化貢獻，參照文獻[7]和文獻[11]，λ和η在所有實驗中均設為：λ=0.077 5，η=0.141 4。

為了生成字典，使用具有0.7 m空間分辨率的QuickBird全色圖像，從http：//glcf.umiacs.umd.edu/data/quickbird/網站上下載20幅PAN圖像，它們不相關，并且不與測試圖像重疊。這些圖像是由因子為3的均值濾波器下采樣，以便擁有與增強HS數據相似的空間分辨率。隨后，隨機取樣 10 000 個原始8×8小塊，利用這些小塊，由K-SVD算法訓練字典， OMP算法用于稀疏編碼。圖1所示為用于生成字典的PAN圖像。

圖1 用于重建字典的PAN圖像

圖2所示為基于SRSR算法、基于MMAP算法、基于ETV算法、基于SRCIP算法和本文算法(SRNS)的空間超分辨率重建結果。僅顯示出了中心在675和2 018 nm的2個光譜帶的結果。圖3所示為圖2的細節。PSNR，SSIM和FSIM的量化評估如圖4所示。表1顯示了不同算法的SAM和ERGAS值。本文算法SRNS的各個評估指標(PSNR,SSIM,FSIM,SAM和ERGAS)均優于其他超分辨率算法。此外，從圖2～圖3可以看出，利用本文算法重建后的飛機、道路、屋頂、草地比其他重建算法更清晰，邊緣也更加尖銳。

圖2 San Diego數據庫的空間分辨率重建結果

圖3 圖2中的細節

對比項MMAPSRCIPETVSRSRSRNSSAM51335602405143493231ERGAS49315731420143192969

圖4 San Diego數據集由不同空間分辨率增強算法得到的結果

本文算法的一個主要優點是，它為每個塊從訓練的字典中選擇原子項，稀疏調整確保這些小塊可以通過字典中最相關的原子項來表示給定的HS數據，在整個觀察到的場景中有許多非局部重復物質，它們具有相似的光譜和空間結構，此類非局部重復信息對改善重建質量有效。本文算法聯合利用了光譜和空間信息，基于從原始低空間分辨率HS圖像提取的端元，因此，最新重建的HR HS數據也良好保留了源圖像的空間和光譜信息。

2.3 Hyperion數據集

Hyperion圖像為307行×307列，共有220條頻帶，空間分辨率為30 μm。AL1 PAN圖像用來訓練字典，AL1 PAN圖像的空間分辨率為10 m，Hyperion和AL1數據可從網站上http：//earthexplorer.usgs.gov/下載。Hyperion和AL1數據也由因子為3的均值濾波器下采樣得到，為了訓練辭典，從10幅 AL1 PAN圖像隨機抽取10 000個原始小塊，其與Hyperion圖像無關。

圖5所示為本文算法與其他方法在第41頻帶(中心波長為762.6 nm)空間分辨率增強的比較結果。圖6顯示了與圖5對應的細節。視覺比較表明，本文算法比其他方法產生更尖銳的邊緣，且增強了圖像的紋理。圖7和表2中相應的量化指標表明本文算法最優。

圖5 Hyperion數據庫的空間分辨率增強結果

圖6 圖5結果的細節

圖7 Hyperion數據集上由不同空間分辨率增強算法得到的結果

對比項MMAPSRCIPETVSRSRSRNSSAM43494721363337403011ERGAS52095140343332702649

3 結語

本文提出了基于稀疏表示和空間譜聯合結構相似的HS和PAN圖像融合算法，主要貢獻是在融合過程中利用非局部端元豐度映射，采用稀疏正則化來解決PAN和HS圖像融合的病態問題求逆過程和設計空間譜聯合正則項，使融合結果更自然。2類不同的HS數據集上的實驗結果表明，本文算法明顯優于傳統分辨率重建算法。

由于本文算法計算復雜度較高，未來將利用優化代碼，使其能在多核處理器上迭代以減少計算時間。

[1] 史云靜， 虞濤， 朱秀昌. 基于訓練集分層的圖像超分辨率重建[J]. 電視技術，2012，36(19)： 18-22.

[2] ZHAO Y， YANG J， ZHANG Q， et al. Hyperspectral imagery super-resolution by sparse representation and spectral regularization[J]. EURASIP Journal on Advances in Signal Processing，2011，17(1)：1-10.

[3] ZHANG H， YANG Z， ZHANG L， et al. Super-resolution reconstruction for multi-angle remote sensing images considering resolution differences[J]. Remote Sensing，2014，6(1)：637-657.

[4] ZHANG H， ZHANG L， SHEN H. A super-resolution reconstruction algorithm for hyperspectral images[J]. Signal Processing，2012，92(9)： 2082-2096.

[5] 趙妍. 基于MAP的高光譜圖像超分辨率方法研究[D]. 哈爾濱：哈爾濱工程大學， 2010.

[6] 楊宇翔， 曾毓， 何志偉，等. 基于自適應權值濾波的深度圖像超分辨率重建[J]. 中國圖象圖形學報，2014，19(8) ： 112-118.

[7] EASON D T， ANDREWS M. Total variation regularization via continuation to recover compressed hyperspectral images[J]. IEEE Trans. Image Processing： a Publication of the IEEE Signal Processing Society，2015，24(1)： 284-293.

[8] SU Y F， FOODY G M， MUAD A M， et al. Combining Hopfield neural network and contouring methods to enhance super-resolution mapping[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing，2012， 5(5)：1403-1417.

[9] MUAD A M， FOODY G M. Impact of land cover patch size on the accuracy of patch area representation in HNN-based super resolution mapping[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing，2012，5(5)： 1418-1427.

[10] ZHANG H， LI J， HUANG Y， et al. A nonlocal weighted joint sparse representation classification method for hyperspectral imagery[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing，2014，7(6)：2056-2065.

[11] 練秋生， 張偉. 基于圖像塊分類稀疏表示的超分辨率重構算法[J]. 電子學報，2012，40(5)：1121-1127.

[12] ZHAO Y， YANG J， ZHANG Q， et al. Hyperspectral imagery super-resolution by sparse representation and spectral regularization[J]. EURASIP Journal on Advances in Signal Processing，2011，2011(1)：1-10.

[13] LI S， YANG B. A new pan-sharpening method using a compressed sensing technique[J]. IEEE Trans. Geoscience and Remote Sensing，2011，49(2)：738-746.

[14] WANG Y H， QIAO J， LI J B， et al. Sparse representation-based MRI super-resolution reconstruction[J]. Measurement， 2014，47(6)：946-953.

王華君(1979— )，講師，碩士，主研圖像處理與模式識別等；

孟德建(1979— )，講師，博士，主研視頻和圖像處理、移動互聯感知等；

姚 湘(1984— )，女，講師，碩士，主研圖像分析、圖像處理等。

責任編輯：閆雯雯

Super-Resolution Image Reconstruction Based on Fusion of Sparse Regularization and NLS

WANG Huajun, MENG Dejian, YAO Xiang

(SchoolofEngineering,TaihuUniversityofWuxi,JiangsuWuxi214064,China)

To maintain spectral consistency and edge sharpness during the processing of super-resolution reconstruction of hyperspectral (HS) images, a joint super-resolution algorithm based on fusion of space spectrum and non-local similarity (NLS) is proposed. Firstly, HS images are used to generate model, and sparse regularization is used to solve the inversion of the ill problem of the reconstruction of panchromatic (PAN) images and HS images. Then, the generated map of abundance coefficients between spatial high resolution and low resolution is analyzed. Finally, space spectrum joint regularization term is designed by non-local similarity. The proposed method is tested with Airborne Visible/Infrared Imaging Spectrometer (AVIRIS) and Hyperion images. Experimental results show that the reconstructed image by this paper is obviously higher than other good algorithms on PSNR, SSIM and FSIM, and lower than other outstanding algorithms significantly on SAM and ERGAS. Proposed algorithm misses the least spectral with only 2% to 3%, which is 30% lower than other algorithms, and the reconstruction results are more natural and clear.

hyperspectral; super-resolution reconstruction; nonlocal similarity; sparse regularization; panchromatic image

江蘇省高校自然科學研究項目(14KJD520009)

TP391.4

A

10.16280/j.videoe.2015.17.007

2015-03-10

【本文獻信息】王華君，孟德建，姚湘.基于稀疏正則化結合NLS的超分辨率圖像重建[J].電視技術,2015，39(17).