快速收斂的EG-LDPC譯碼算法設計實現

張佳巖，張士偉，吳 瑋，張 弛，王 碩

(哈爾濱工業大學 通信技術研究所，黑龍江 哈爾濱 150001)

快速收斂的EG-LDPC譯碼算法設計實現

張佳巖，張士偉，吳 瑋，張 弛，王 碩

(哈爾濱工業大學 通信技術研究所，黑龍江 哈爾濱 150001)

歐氏幾何構造的LDPC碼屬于不可分層的LDPC碼，無法采用TDMP算法譯碼結構，針對該問題設計實現了一種新型分層譯碼器。在Xilinx V5FPGA上實現了碼長為1 023、碼率為0.781 EG-LDPC碼的譯碼器設計。仿真驗證表明：理論上該方法與優化的規范化最小和譯碼算法相比，迭代次數減少一倍，存儲資源消耗得到降低，而誤碼性能幾乎相同。FPGA實現上，譯碼輸出與MATLAB定點仿真給出的結果相同，誤碼性能由于量化和限幅處理與理論值相比約有0.3 dB的損失。在時鐘頻率為50 MHz串行處理各分層時，吞吐量為49.7 Mbit/s。

EG-LDPC；分層最小和譯碼；FPGA

低密度奇偶校驗碼(LDPC)是由Gallager在19世紀60年代提出的逼近香農限的信道編碼[1]，但其并沒有給出高性能LDPC碼校驗矩陣系統的構造方法。Shu Lin和Forssorier基于有限域歐氏幾何理論首次提出了一種系統的構造高碼率LDPC碼的方法[2]，這類碼具有不可分層、準循環形式的校驗矩陣，編碼簡單且適用不同的傳統譯碼算法。LDPC碼在無線通信中應用廣泛，在LTE中使用可保證系統性能[3]。

LDPC碼譯碼算法的研究主要集中在提升誤碼性能，減少譯碼復雜度及加快收斂速度3個方面。文獻[4]提出了一種低復雜度的BP譯碼算法，在迭代過程中只更新可靠度低的節點消息，省去高可靠度的節點消息的計算，從而來提高譯碼算法的收斂速度，但仍避免不了概率域BP算法中乘法運算及對數域BP中的雙曲正切、反正切計算，收斂雖然較快但資源消耗大，不適合硬件實現。文獻[5]提出了整數量化最小和譯碼算法，易于硬件實現，通過新增額外校驗因子使誤碼性能提高，但在高信噪比下與連續譯碼存在差距。文獻[6]首次提出把Turbo譯碼消息傳遞機制應用到LDPC譯碼中的TDMP算法，誤碼性能良好，收斂速度快，但不適用不可分層LDPC碼。針對該問題，結合TDMP的消息傳遞機制與NMSA算法[7]提出了一種分層NMSA算法并對其進行FPGA實現。該算法誤碼性能較好，最大迭代5次即可，較文獻[8]中迭代30次相比，能夠有效減少譯碼延遲和資源消耗。

1 EG-LDPC校驗矩陣的構造

本設計基于m=2，s=5的歐氏幾何構造的校驗矩陣。構造EG-LDPC碼校驗矩陣具體步驟如下：

步驟1：根據碼長和碼率等參數確定歐氏幾何的參數m和s，計算GF(2ms)的本原元α及其子域GF(2s)本原元β。

步驟2：創建一個向量v，向量的元素為子域GF(2s)中的所有元素，v向量記錄了EG(m,2s)中一條過原點的直線上的點。

步驟3：構造出EG(m,2s)歐氏空間中所有過原點的直線所對應的向量。

α·v,α2·v,…,αn·v(n=2ms/2s)

(1)

步驟4：取出任意一條過原點直線對應的向量αi·v，進行以下計算

x+αi·vx∈GF(2ms)

(2)

即可得到與直線αi·v平行的所有直線對應的向量。取不同的值計算結果可能出現重復，如果重復則去掉，不重復則保留。遍歷步驟3中的所有向量，即可求出EG(m,2s)歐氏幾何上所有直線對應的保存著直線上點的向量。

步驟5：計算EG(m,2s)歐氏幾何上所有直線的關聯向量L。創建一個向量，向量的大小與歐氏幾何中點的數目相同，L的每個元素與GF(2ms)域上的元素一一對應，取出步驟4中的一個向量Γ，把L中與Γ中元素相對應的位置置1，其他位置置0，遍歷步驟4中的所有向量，就構造出了EG(m,2s)歐氏幾何中所有直線的關聯向量。

步驟6：去掉所有過原點的直線的關聯向量并去掉原點，就得到了EG-LDPC碼的奇偶校驗矩陣H。

對于m=2，校驗矩陣H只有一個循體。當m大于2時，校驗矩陣存在(2(m-1)s-1)/(2s-1)個循環體。取出校驗矩陣H的一個行向量γ，對其進行2ms-2次循環移位，對所得向量縱向排列就得到了一個循環體。從校驗矩陣H中去掉該循環體中的所有向量，在校驗矩陣H余下的向量中再取出一個向量，進行同樣的處理，直到處理完矩陣H的所有向量。然后對每個循環體進行橫向排列就得到了基于有限域歐氏幾何的QC-LDPC碼的校驗矩陣Hqc。通過以上步驟得到了EG-1 023 LDPC碼的校驗矩陣H。

2 改進的分層最小和譯碼算法

記R,q,r分別為變量節點后驗概率對數似然比，校驗節點到變量節點消息，變量節點到校驗節點消息。yi,σ2分別為信道輸入的采樣值，信道中高斯白噪聲的方差。采用BPSK的調制方式。l為迭代次數，k為第幾層。校驗矩陣的一行即為一個分層。對于高行重的EG-LDPC碼，規范化系數一般取值較小[9-10]，大約為0.25。為了節省硬件資源減少開銷，本設計中規范化系數α取0.5。

1)初始化

(3)

2)迭代過程

(4)

(5)

(6)

3)判決譯碼

在每次迭代結束時，根據對接收碼字做出硬判決

(7)

如果HCT=0成立，終止迭代，否則進行下一次迭代，直到達到最大迭代次數。該算法以規范化最小和譯碼算法為基礎，采用Turbo譯碼消息傳遞機制，使上層更新的信息及時得到利用，從而加快收斂速度。只需通過實時的加法運算即可更新變量節點，節省了存儲資源，更利于硬件實現。

3 譯碼器結構設計、仿真及分析

3.1 校驗節點處單元

圖1 校驗節點處理單元結構圖

3.2 最小值計算模塊

該模塊輸出32個CTV絕對值中的最小值、次小值和最小值編號[11]。該結構由比較器和連接單元構成，詳見參考文獻[11]。仿真結果如圖2所示，輸入data0～data31，data1為0是最小值，可以看到index為1，求出最小值min_1st為0，次小值min_2st也是0。計算結果存儲到RAM中，絕對值量化為4 bit，共有1 023層，最小值和次小值消耗8 kbit的存儲資源，Index用5 bit來表示，供需消耗5 kbit的存儲資源。還需存儲的符號，每層32個，需要消耗32 kbit。需要的存儲單元共為45 kbit，存儲資源的消耗相當小，而碼長更長如(4 599， 4 227)的EG-LDPC碼存儲資源的消耗與本文中的(1 023， 781)的EG-LDPC碼存儲資源消耗是相同的。

圖2 最小值計算模塊結果(截圖)

3.3 譯碼器工作過程

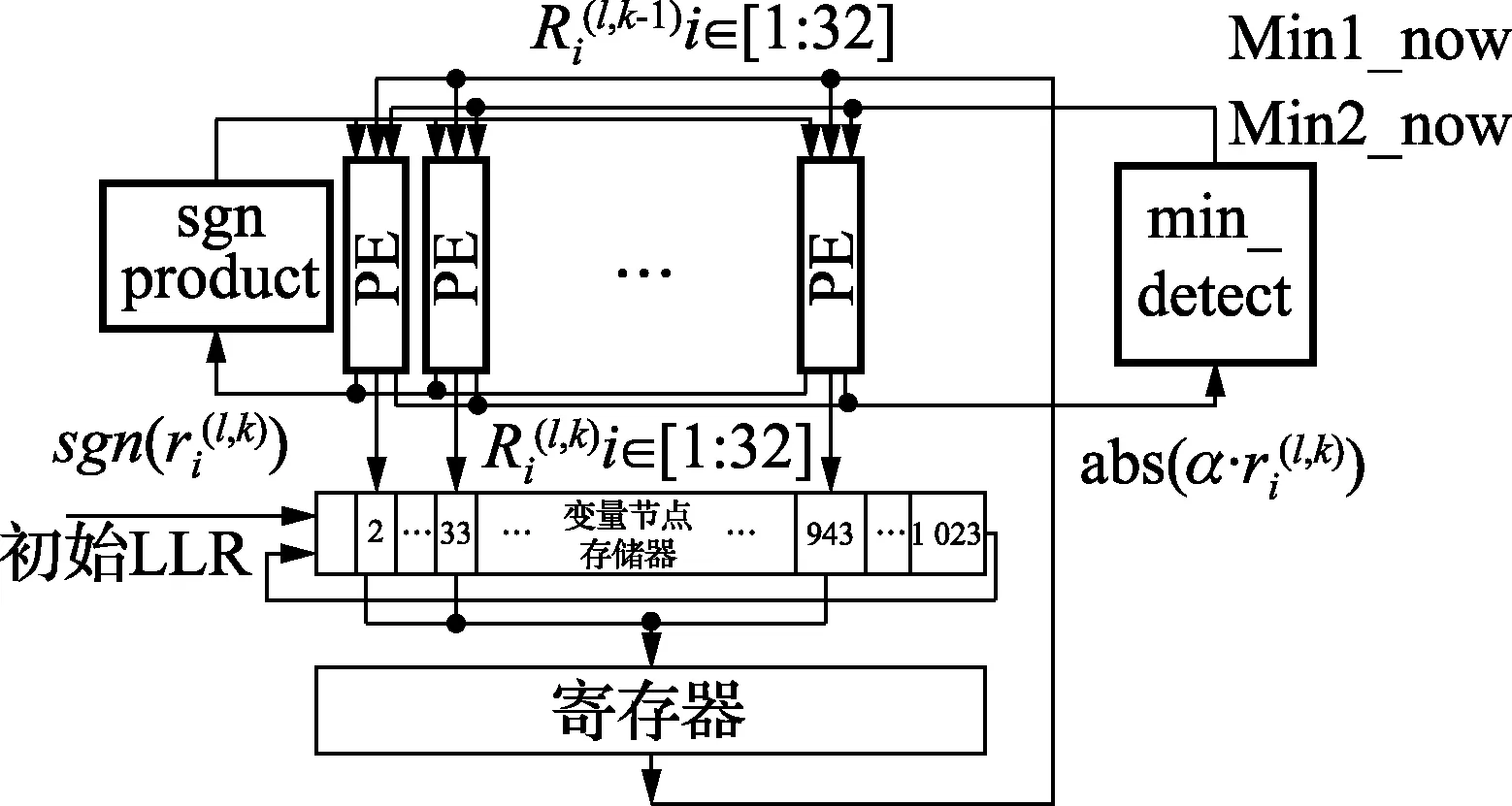
圖3 譯碼器結構圖

圖4 譯碼輸出結果(截圖)

理論誤碼性能(α=0.5)與硬件實現的誤碼性能對比如圖5所示。由于初始化信息與變量、校驗節點信息量化的影響，硬件實現與理論大概有0.3 dB的誤碼性能損失。

圖5 理論與硬件誤碼性能

對于(1 023，781)的EG-LDPC碼，規范化系數取0.25時，此算法誤碼性能最優，在迭代5次時比概率域BP譯碼算法迭代50次時有0.2 dB的編碼增益，比對數域BP算法約有0.3 dB的增益，比最小和譯碼算法(min-sum)約有2 dB的編碼增益，如圖6所示。所以該算法誤碼性能良好且具有較快的收斂速度，從而減小了硬件實現時的譯碼延遲。

圖6 與其他譯碼算法誤碼性能對比圖

4 小結

該譯碼器在平均迭代2～3次即可收斂，硬件實現時誤碼性能由于量化和計算過程中的限幅處理，與理論相比僅有0.3 dB的損失，資源消耗僅為45 kbit，譯碼延遲小，在串行情況50 MHz時鐘下吞吐量達到49.7 Mbit/s，進行一定的并行處理吞吐量將更高。如果初始化信息和中間計算結果量化位數增多，可以選擇修正因子為0.25，誤碼性能會得到進一步提高。

[1] 晏堅，何元智，潘亞漢，等.差錯控制編碼[M].北京：機械工業出版社，2007.

[2] KOU Yu， LIN Shu，FOSSORIER M P C. Low-density parity-check codes based on finite geometries： a rediscovery and new results[J]. IEEE Trans. Information Theory， 2001，47(7)：2711-2736.

[3] LAO L， LI L， ZHU M， et al. The improved Turbo-decoding Message-passing algorithm and corresponding decoder for LDPC based on LTE[C]//Proc. IEEE International Conference on Signal Processing， Communications and Computing (ICSPCC). [S.l.]：IEEE Press，2014： 890-894.

[4] 郭銳，劉濟林.LDPC碼的一種低復雜度BP譯碼算法[J].浙江大學學報：工學版，2008，42(3)：450-455.

[5] 馬匯淼，馬林華，張嵩，等.基于整數運算的LDPC碼改進最小和譯碼算法[J].電視技術，2013，37(17)：197-199.

[6] MANSOUR M M，SHANBHANG N R. High throughput LDPC decoders[J]. IEEE Trans. Very Large Scale Integration Systems， 2003(11)：976-978.

[7] 楊知行，林之初，王軍，等.準循環LDPC碼的半并行譯碼器設計[J].電視技術，2006，30(2)：24-26.

[8] YAN Ying，DAN Bo，HUANG Shuangqu. A cost efficient LDPC decoder for DVB-S2[C]//Proc. IEEE 8th International Conference on ASIC. [S.l.]：IEEE Press，2009：1007-1010.

[9] CHEN Jinhu，MARC P C. Fossorier near optimum universal belief propagation based decoding of low-density parity check codes[J]. IEEE Trans. Communications， 2002，50(3)：406-414.

[10] 馬匯淼，馬林華，田雨. 基于改進的分層譯碼算法的QC-LDPC譯碼器設計[J].電子技術應用，2012，38(7)：51-53.

[11] WEY C-L， SHIEH Ming-Der，LIN Shin-Yo. Algorithms of finding the first two minimum values and their hardware implementation[J]. IEEE Trans. Circuits and Systems I： Regular Papers，2008，55(11)：3430 -3437.

張佳巖(1974— )，副教授，碩士生導師，主要研究方向為信道編解碼、擴頻、深空通信技術；

張士偉(1990— )，碩士生，主研信道編碼技術；

吳 瑋(1981— )，博士，講師，主研無線自組網、LTE/LTE-A移動通信系統；

張 弛(1990— )，碩士生，主研擴頻信號快速捕獲、跟蹤技術。

王 碩(1992— )，女，碩士生，主研跳頻系統FPGA實現技術。

責任編輯：閆雯雯

Implementation of Efficient Convergence EG-LDPC Decoding Algorithm

ZHANG Jiayan, ZHANG Shiwei,WU Wei,ZHANG Chi,WANG Shuo

(CommunicationResearchCenter,HarbinInstituteofTechnology,Harbin150001,China)

For TDMP decoding structure is not applicable to LDPC code which is constructed based on finite field Euclidean geometry, a new layered decoder structure is proposed. The design can be able to decode the EG-1023 LDPC which code rate is 0.781 on Xilinx V5 FPGA. The simulation results show that on theory the speed of convergence is twice as quick as the optimal normalized min-sum algorithm and memory resources cost decreases, but the error performance does not change. When implemented on the FPGA, the error performance has a loss about 0.3 dB because of quantization and amplitude limiting. The throughput is 49.7 Mbit/s working on the 50 MHz clock.

EG-LPDC; layered min-sum algorithm; FPGA

國家自然科學基金項目(61201147)；國家科技重大專項項目(2012ZX03003011-004)

TN911

A

10.16280/j.videoe.2015.17.023

2015-04-06

【本文獻信息】張佳巖，張士偉，吳瑋，等.快速收斂的EG-LDPC譯碼算法設計實現[J].電視技術,2015，39(17).