考慮收斂變形的通縫拼裝盾構隧道縱向等效抗彎剛度計算分析

李成強，郭 冰，李明宇，王志良

(1.中鐵工程設計咨詢集團有限公司交通分院，河南 鄭州 450000;2.河南東龍控股有限公司，河南 鄭州450046;3.鄭州大學土木工程學院，河南鄭州 450001;4.昆明理工大學土木工程學院，云南昆明 650500)

0 引言

對于通縫拼裝盾構隧道，環間接縫大大降低了襯砌結構的剛度，當隧道發生不均勻縱向變形時，在環縫處往往會產生管片張開和錯臺，進而導致接縫滲漏水，嚴重時會造成管片開裂、軌道不平順等情況，危及隧道的運營安全。因此，為了確保運營期盾構隧道結構的安全使用，分析研究通縫拼裝盾構隧道長期沉降規律和縱向變形分布特征具有非常重要的實用價值，但至今對此的研究甚少。在運營地鐵隧道長期沉降過程中，隧道內橫縱向管片或接縫的變形和受力往往伴生存在。隨著隧道縱向不均勻沉降的增加，隧道收斂變形也逐步變化。為此，在通縫拼裝盾構隧道縱向變形和受力進行研究的同時，應考慮隧道收斂變形對襯砌結構縱向變形和受力的影響。志波由紀夫先后于1988年和1989年提出詮釋通縫拼裝盾構隧道縱向變形和受力的等效連續化力學計算模型，模型中考慮將通縫隧道結構等效為均質圓筒，通過計算得出均質圓筒的等效剛度，其中包括等效軸向抗拉剛度和等效抗彎剛度;文獻［1］對志波由紀夫提出的模型進行了修正，進一步給出了連接螺栓塑性狀態下等效抗彎剛度計算方法，并進行了參數分析;文獻［2］引入工程實例對文獻［1］提出的模型進行了驗證;文獻［3］采用規范方法對環縫處受力和變形進行了分析;文獻［4］在文獻［1－2］基礎上進一步考慮接縫處螺栓受拉時對螺栓孔處混凝土受力的影響，引入了環縫影響系數，并進了參數分析。上述文獻雖然均對等效抗彎剛度計算模型進行了研究，但所提出的方法中均未考慮隧道變形的影響，即隧道發生橫向變形時，通縫拼裝盾構隧道縱向變形和受力特征。為此，本文根據對已運營的上海地鐵8號線西藏北路站—中興路站隧道進行為期1年的變形監測，并將隧道收斂變形和接縫張開量監測數據引入到文獻［1］提出的模型中，重新進行分析計算，提出考慮隧道收斂變形的縱向等效抗彎剛度模型，該模型能更準確地詮釋通縫拼裝盾構隧道結構縱向的變形和受力，為運營地鐵盾構隧道結構的安全評判提供價值更高的理論參考依據。

1 現場實測試驗

1.1 工程概述

上海軌道交通8號線西藏北路站—中興路站隧道，采用通縫拼裝方式。環片由小封頂、3塊標準塊、2塊鄰接塊構成，環寬1.2 m、內徑5.5 m、外徑6.2 m、壁厚0.35 m。管片強度等級為C55，抗滲等級為1.0 MPa，接縫處均采用M30彎螺栓連接，其中環縫17根，縱縫12根。接縫防水均采用EPDM(三元乙丙)為主，輔以遇水膨脹橡膠的復合密封墊。

監測試驗段分為旁通道、標準段、洞口。現場試驗監測段地質剖面如圖1所示。分別對道床和管片沉降、隧道收斂、以及環縫張開量進行了為期1年的實測，監測布點示意如圖2所示。道床沉降監測頻率為1次/6個月，其他3項監測頻率為1次/3個月。隧道收斂采用人工全站儀方法［5］，通過掃描襯砌環上50個點位，得到相應的初始坐標，隨后借鑒文獻［6－9］的方法進行擬合，得出隧道收斂變形;道床和管片的沉降采用二等水準測量方法;管片之間的接縫張開量采用裂縫計進行量測。監測項目測點編號見表1。

圖1 現場試驗監測段地質剖面圖Fig.1 Profile showing geological conditions of monitoring section of tunnel

圖2 監測布點示意圖Fig.2 Layout of monitoring points

表1 現場監測試驗段監測項目編號表Table 1 Monitoring items

1.2 數據分析

圖3給出了監測試驗段左側標準塊年沉降變化量及相鄰管片沉降差。隨著時間的推移，管片沉降量在逐漸增加。沿隧道縱向，由于周圍地質條件和外部環境相比單一環斷面的情況更加復雜，多數情況下會使整體結構在長期沉降過程中產生縱向不均勻沉降變形。

圖4分別給出了2008年6月和12月及2009年2月和5月各試驗監測段盾構隧道內徑和橢圓度的監測結果。隨著時間的推移，隧道發生豎向壓縮變形，又稱“橫鴨蛋”。旁通道處隧道收斂變形量最大，洞口最小。盾構施工和凍結法施工2次施工擾動疊加作用，導致旁通道隧道收斂增大，此后列車振動進一步加大和延長了擾動土的固結壓縮變形和固結時間。

洞口處，端頭井對隧道的約束，加上進出洞的加固，限制了附近隧道的收斂變形。

2 修正縱向抗彎剛度計算模型

基于現場試驗中隧道收斂變形的數據特征，綜合考慮運營地鐵盾構隧道長期沉降過程中，橫、縱向變形的相互影響與作用。將隧道收斂變形引入等效連續化縱向抗彎剛度模型的計算分析中。

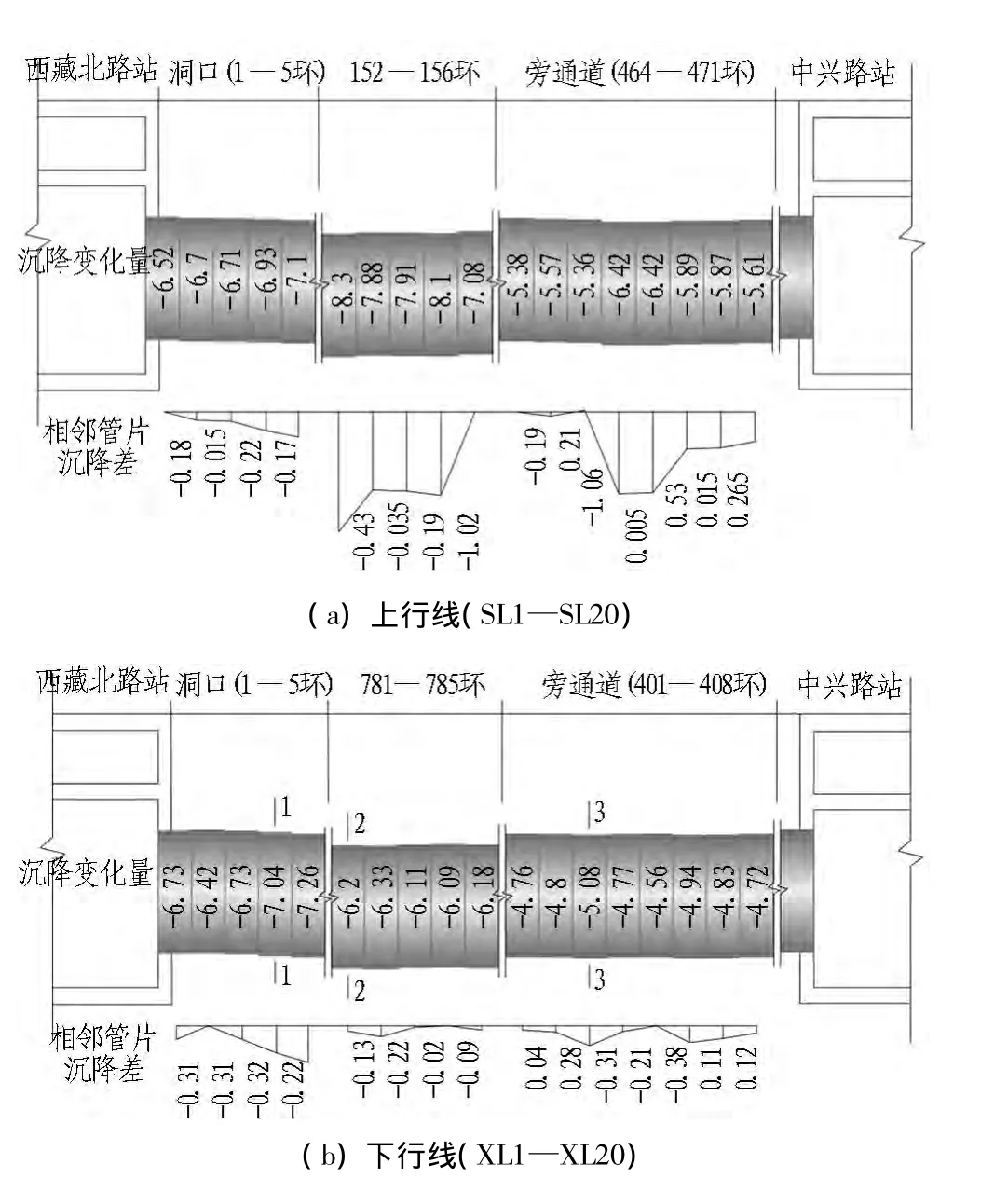
圖3 左側標準塊沉降變化量和相鄰管片沉降差(單位:mm/年)Fig.3 Settlement variation of the left standard segment and settlement difference between neighboring segments(mm/年)

圖4 隧道收斂分布曲線Fig.4 Distribution curves of tunnel convergence

2.1 模型計算假定

借鑒文獻［1］，當單元受到彎矩M作用時，接頭兩側相鄰襯砌環的2個平面發生相對轉角θ，θ/ls即為梁彎曲的理論曲率。模型單元彎曲示意如圖5所示。

圖5 模型單元彎曲示意圖［1］Fig.5 Bending diagram of model elements［1］

為求出彎矩和曲率之間的關系，作以下假定:1)平截面假定，即襯砌環為均質圓環，橫截面上每一點的變形與中性軸距離成正比，截面上各點的應力分布沿隧道縱向不發生變化，不考慮環間錯臺(踏步)對縱向螺栓和凹凸榫的剪切作用。2)彎矩作用下在環縫部位，受拉區拉力由螺栓全部承擔，受壓區壓力由管片全部承擔。

為方便計算，螺栓以沿襯砌圓環連續均勻分布的彈簧來模擬，即:

式中:Kr為接頭螺栓的平均線剛度，kN/m;As為接頭螺栓橫截面的面積，m2;Es為接頭螺栓彈性模量，MPa;ll為連接螺栓長度，m。

當截面處于完全彈性狀態且所有螺栓承受的拉力均小于Py時［1］，單元應力和應變如圖6所示。根據變形協調條件和力平衡方程得到單元彎矩和曲率的關系。

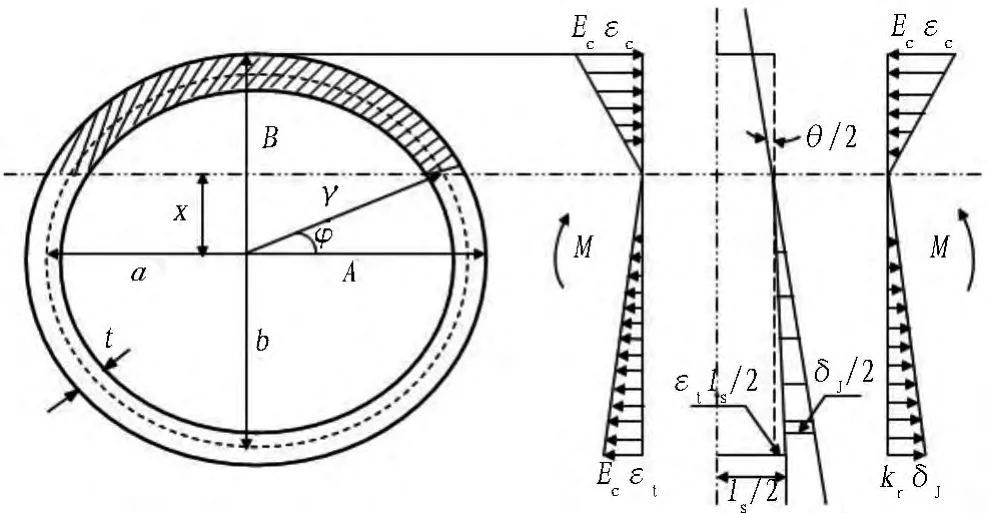
圖6 彈性狀態時的應力應變圖Fig.6 Elastic stress and strain

2.2 考慮收斂變形的縱向等效抗彎剛度計算過程

變形協調條件:

式中:a，b為襯砌橢圓環平均半徑的長半軸和短半軸，a=(t+d+ ΔDl)/2，b=(t+d+ ΔDv)/2，m;ΔDl，ΔDv為隧道收斂變形，ΔDl＞ 0，ΔDv＞ 0，mm;d，D為襯砌圓環內外徑，m;t，ls為管片厚度和環寬，m;A，B為襯砌橢圓環外徑的長半軸和短半軸，A=a+t/2，B=b+t/2，m;ε為橢圓圓心率;r為襯砌環任意位置處平均半徑，r=為中性軸的位置，其中 φ =sin－1(x/r);εt，εc為管片的拉應變和壓應變;θ為截面相對轉角，°;δJ為連接縱向螺栓的最大變形量，mm;Ec為襯砌環彈性模量，MPa。

聯立式(2)—(5)解得:

式中θeq為等效連續梁相對轉角，°。

對比式(6)和式(7)得到隧道的等效彈性彎曲剛度為:

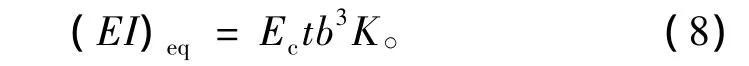
彈性極限彎矩My可比較式(9)給出:

式(11)—(15)中:σt，σc為受拉和受壓區管片最大拉、壓應力，MPa;My為彈性極限彎矩，kN·m;σs為受拉區連接螺栓最大拉應力，kN;δT為受拉區環縫最大張開量，mm;ρ為曲率半徑，m;δ0為因襯砌拼裝導致的環縫張開量，mm;dl，ll為縱向螺栓直徑和長度，m;Es為縱向螺栓彈性模量，MPa;Ζ為考慮環縫處螺栓孔應力集中和剪切荷載對螺栓受力的影響，對螺栓彈性模量進行適當折減(0＜ζ＜1)。

2.3 實例分析

多項式分段擬合圖3管片沉降數據，得到監測試驗段隧道縱向變形最小曲率半徑ρmin=3.33×105m。環縫張開量監測與計算對比結果如表2所示。

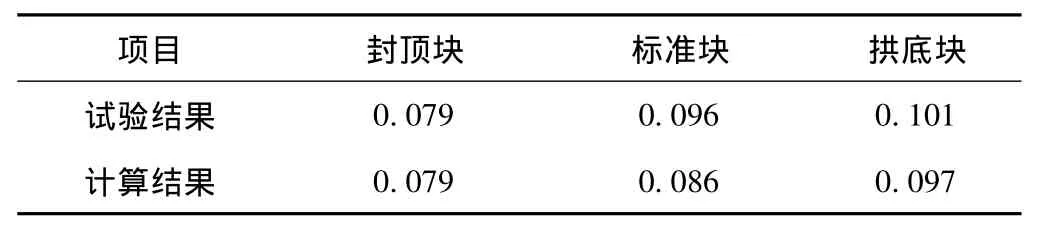
表2 張開量監測與計算結果對比Table 2 Comparison and contrast between measured opening of ring joints and calculated opening of ring joints mm

3 參數靈敏度分析

參數靈敏度分析仍依托本次現場監測試驗對象，計算參數如表3所示。

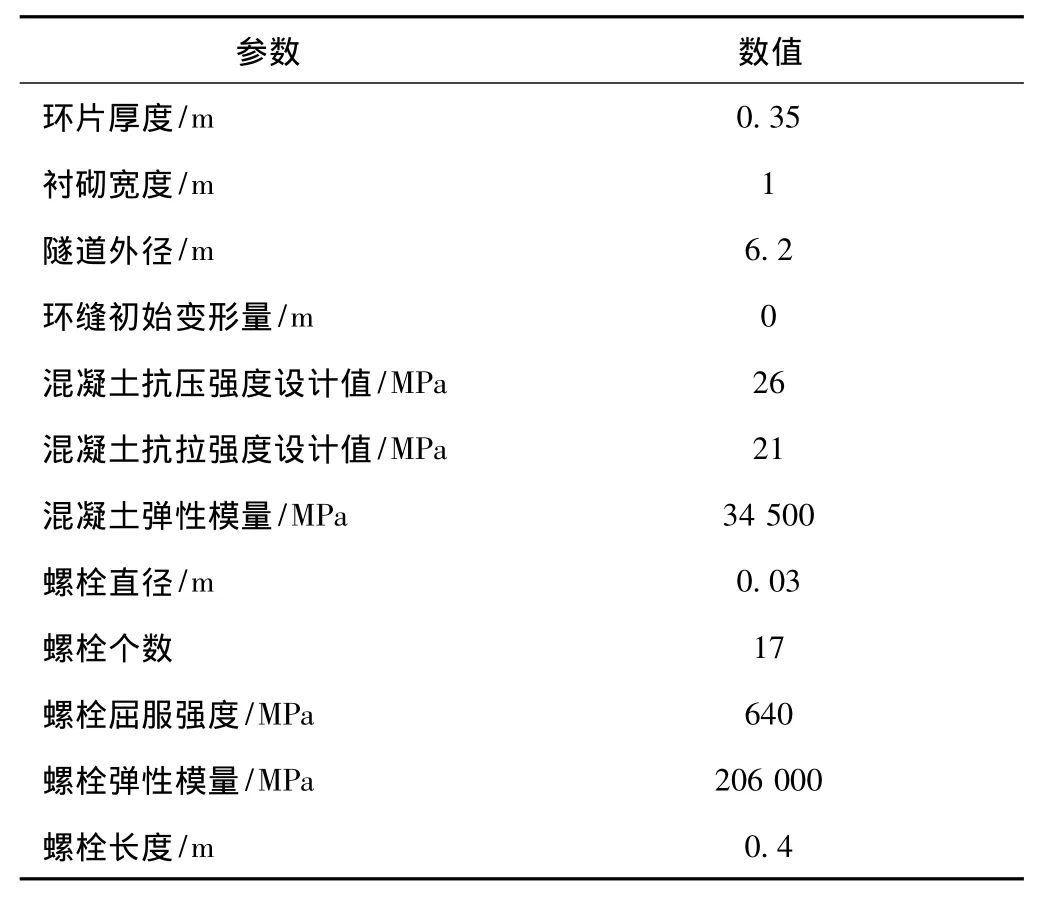
表3 計算參數Table 3 Calculation parameters

圖7—10給出了不同隧道收斂變形下曲率半徑與隧道結構受力和變形的關系曲線。在環縫處不考慮剪切作用，在彎曲狀態下，隨著收斂變形的增加，環縫最大張開量和內力均有所減小。結構縱向變形曲率半徑越小，隧道收斂變形對其影響越顯著。在大曲率半徑隧道結構縱向變形狀態下，隧道收斂變形對結構縱向變形的影響可以忽略。

圖7 隧道收斂與環縫張開量關系曲線Fig.7 Relationship between segment ring joint opening and tunnel convergence

4 對比分析

表4和表5取GB 50446—2008《上海地鐵保護條列》和《盾構掘進隧道工程施工及驗收規范》規定的ρmin=15 000 m和fT=6.4×105kPa分別進行計算對比分析。計算中ΔDl=31 mm，ΔDv=31 mm;δ0=0;ζ=1。相同縱向曲率或曲率半徑下，環縫張開量δT:文獻［4］＜本文計算方法＜文獻［2］＜文獻［3］;連接螺栓應力fT:本文計算方法＜文獻［2］＜文獻［3］＜文獻［4］。

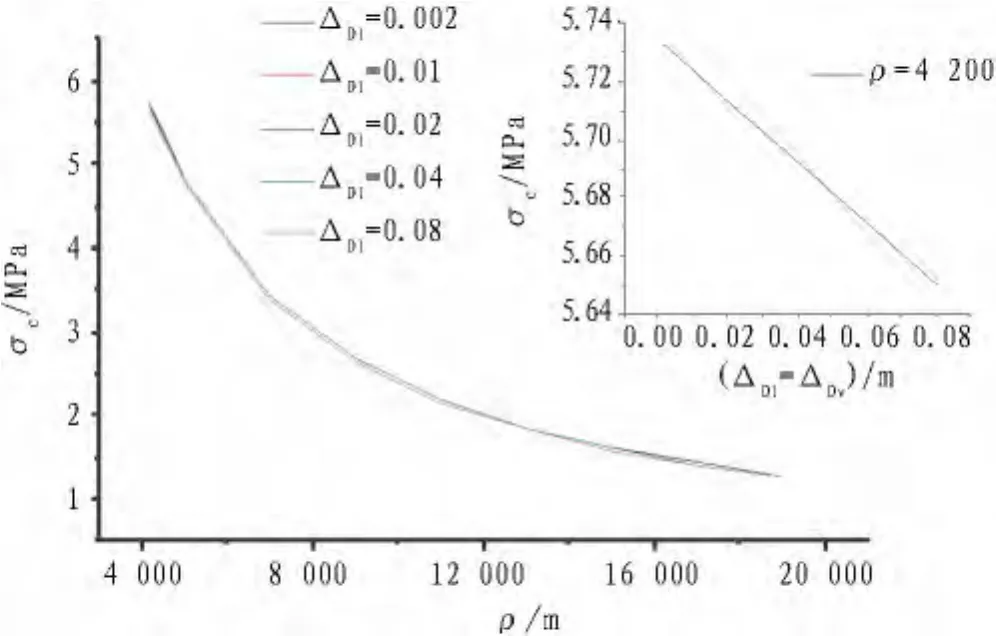
圖8 隧道收斂與管片壓應力關系曲線Fig.8 Relationship between segment compression stress and tunnel convergence

圖9 隧道收斂與管片拉應力關系曲線Fig.9 Relationship between segment tensile stress and tunnel convergence

圖10 隧道收斂與螺栓拉應力關系曲線Fig.10 Relationship between longitudinal tensile stress of bolts and tunnel convergence

環縫縱向連接螺栓最大拉應力相等時，環縫張開量δT:文獻［4］＜文獻［2］＜本文計算方法 ＜文獻［3］;縱向曲率半徑ρ:文獻［3］＜本文計算方法＜文獻［2］＜文獻［4］。

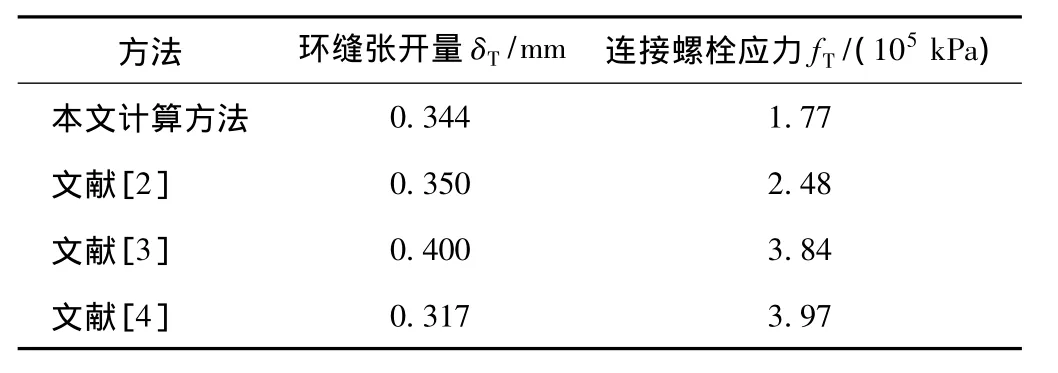
表4 對比分析表(ρmin=15 000 m)Table 4 Comparison table(ρmin=15 000 m)

表5 對比分析表(fT=6.4×105kPa)Table 5 Comparison table(fT=6.4×105kPa)

5 結論與展望

依托上海運營軌道交通8號線西藏北路—中興路隧道現場監測試驗結果，考慮隧道收斂變形對通縫拼裝地鐵盾構隧道內襯砌環縫處變形和受力的影響，對縱向等效剛度模型進行了修正計算與分析，并將其結果與現有相關計算方法進行了對比，得出如下結論。

1)現場試驗監測數據特征表明，在盾構隧道長期沉降過程中，其結構發生橫向變形的同時，伴隨著縱向變形的產生。襯砌結構橫縱向變形和受力相輔相成，且隧道收斂變形最大值和最小值分別出現在旁通道和工作井附近。

2)修正等效抗彎剛度計算表明:環縫位置不考慮剪切作用時，彎曲狀態下，隨著隧道收斂變形的增加，環縫最大張開量、螺栓應力、管片拉壓應力均略有減小;結構縱向變形曲率半徑越小，隧道收斂變形對結構受力和變形影響越顯著;在隧道結構縱向變形曲率半徑較大時，隧道收斂變形對結構的影響可以忽略。

本文提出的修正計算模型，與以往研究結果不同，充分考慮了襯砌結構橫縱向變形和受力影響問題，通過現場試驗數據和已有文獻的對比驗證，證實了該模型能相對更準確地詮釋純彎曲狀態下通縫拼裝盾構隧道縱向變形和受力特征。但所提出模型中未考慮螺栓屈服時結構縱向的變形和受力問題，此外，本次僅是對純彎狀態下通縫拼裝盾構隧道結構受力問題進行了研究，未考慮當接縫受剪時的此類隧道等效抗剪剛度的計算方法，對于其不足仍需要在今后的研究中進一步改進。

［1］ 林永國.地鐵隧道縱向變形結構性能研究［D］.上海:同濟大學地下建筑與工程學院，2001.(LIN Yongguo.Performance research on structural longitudinal deformation of Metro tunnel［D］.Shanghai:School of Civil Engineering，Tongji University，2001.(in Chinese))

［2］ 鄭永來，韓文星，童琪華，等.軟土地鐵隧道縱向不均勻沉降導致的管片接頭環縫開裂研究［J］.巖石力學與工程學報，2005，24(24):4552 －4558.(ZHENG Yonglai，HAN Wenxing，TONG Qihua，et al.Study on longitudinal crack of shield tunnel segment joint due to asymmetric settlement in softsoil［J］.Chinese JournalofRock Mechanics and Engineering，2005，24(24):4552－4558.(in Chinese))

［3］ 葉耀東.軟土地區運營地鐵盾構隧道結構變形及健康診斷方法研究［D］.上海:同濟大學結構工程學院，2007.(YE Yaodong.Research on deformation and method of health diagnose of operational subway structures in soft soil［D］. Shanghai:SchoolofCivilEngineering，Tongji University，2007.(in Chinese))

［4］ 魯志鵬.基于靜態量測數據的盾構法地鐵隧道建設和運營安全評價研究［D］.上海:同濟大學巖土工程學院，2008.(LU Zhipeng.The safety evaluation research of metro shield tunnel during construction and operation based on static measured data［D］.Shanghai:School of Geote-chnical Engineering，Tongji University，2008.(in Chinese))

［5］ 晏成.全站儀在隧道變形監測中的應用研究［D］.上海:同濟大學結構工程學院，2005.(YAN Cheng.The application of total station in tunnel deformation monitoring［D］. Shanghai:SchoolofCivilEngineering，Tongji University，2005.(in Chinese))

［6］ 丘維聲.解析幾何［M］.北京:北京大學出版社，1999.(QIU Weisheng.Analytic geometry［M］.Beijing:Peking University Press，1999.(in Chinese))

［7］ P L Rosin.A note on the least squares fitting of ellipses［J］.Pattern Recognition Letters，1993(14):799 －808.

［8］ W Gander，G H Golub，R Strebel.Least-square fitting of circles and ellipses［J］.BIT，1994(43):558 －578.

［9］ G Taubin.Estimation of planar curves，surfaces and nonplanar space curves defined by implicit equations with applications to edge and range image segmentation［J］.IEEE Trans Pattern Analysis and Machine Intelligence，1991，13(11):1115 －1138.