鼓形齒聯接關鍵問題的探討
劉學明
(SEW-工業減速機(天津)有限公司,天津 300457)
0 引言
與直齒式聯軸器相比,鼓形齒式聯軸器有以下特點:1)承載能力強。在相同的內齒套外徑和聯軸器最大外徑下,鼓形齒式聯軸器的承載能力平均比直齒式聯軸器提高15%~20%;2)角位移補償量大。在相同的模數、齒數、齒寬下,鼓形齒比直齒允許的角位移大;3)鼓形齒面使內、外齒的接觸條件得到改善,避免了在角位移條件下直齒齒端棱邊擠壓,造成應力集中的弊端,同時改善了齒面摩擦、磨損狀況,降低了噪聲,減少了維修周期;4)外齒套齒端呈喇叭形狀,使內、外齒裝拆十分方便;5)傳動效率高達99.7%。基于以上特點,國內外已普遍以鼓形齒聯軸器替代直齒式聯軸器。依靠其傳動力矩大、傳遞效率高、偏轉角大、壽命長、傳動平穩等特點被廣泛應用于冶金、礦山等重工業。
對于較長距離的驅動和被驅動部件需要用較長的鼓形齒式聯軸器來進行連接,而鼓形聯軸器本身除了齒部的幾何設計外,我們還要關心齒套與長軸連接對齒部參數的影響。
以圖1為例,討論齒套裝入軸上涉及到的一些具體問題。為了達到實際應用(傳遞力矩)的目的,我們必須對其尺寸進行設計。
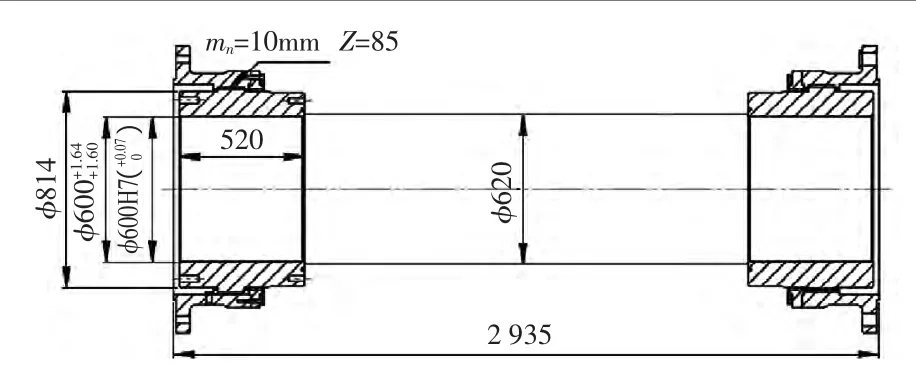
圖1 聯軸器剖分圖
1 滿足使用要求
1.1 強度計算
1)計算轉矩。聯軸器強度計算應該考慮各因素影響,采用計算轉矩Tc進行修正:
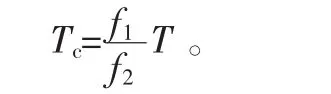
式中:f1為動載系數,受載荷狀況及工作時間影響,f1=1~2;f2為偏載系數,受聯軸器規格、角位移及轉速影響,fz=0.2~1;本案例要求T=3780000N·m。
2)接觸強度校核。如圖2所示,在軸線無角位移時,鼓形齒只有齒的中間凸起部分接觸,內外齒在中間截面上可認為沿齒高均勻接觸,接觸區壓應力呈橢圓分布:由赫茲公式得接觸強度的校核公式式中,σHP為材料的許用接觸強度,MPa;φe為曲率系數,R為曲率半徑(見圖3)。
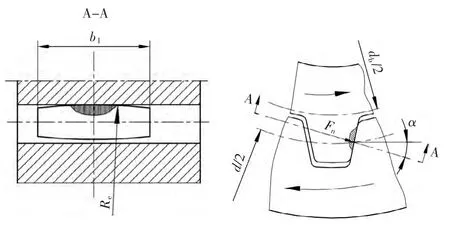
圖2 接觸應力示意圖
3)剪切強度校核。齒輪聯軸器的彎曲強度一般不做校核,僅校核剪切強度,公式為
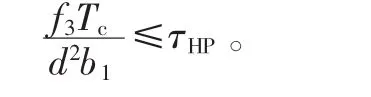
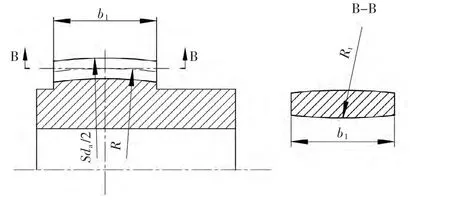
圖3 鼓形齒的位移圓半徑
式中,τHP為材料的許用切應力。
4)熱處理工藝。對于承受大扭矩的齒部聯接必須考慮良好的耐磨性和良好的表面硬度,同時還要求能抵抗瞬時的沖擊,因此齒部必須進行硬化處理。對于通常使用的中碳鋼材料,齒部要進行表面淬火或者表面氮化處理。
1.2 滿足偏轉角的要求
1)聯軸器內外齒的定心方式一般采用內齒齒根圓與外齒齒頂圓定心,中、低速時配合取H9/e8;為了得到所需要的側隙以滿足偏轉角的要求,我們用第一種標準型刀具加工方法:外齒不變位x=0、齒頂高ha=mn、齒根高hf=1.25,內齒齒根高 hf=mn、齒頂高 ha=(0.8~1)mn;基于齒形聯軸器的通常要求初步設定整體的偏轉角△α=1.6°;結合強度要求我們可以得到鼓形聯軸器的基本參數mn=10mm,z=85,α=20°;
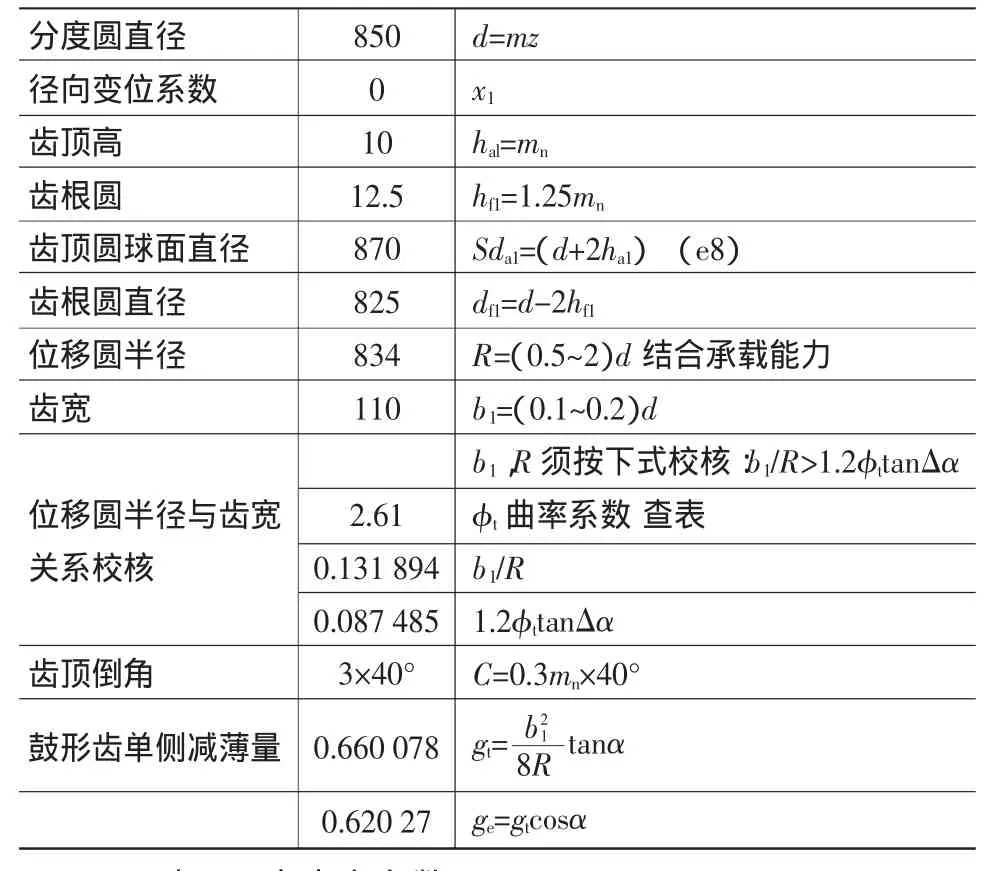
表1 外齒套參數

表2 內齒套參數
2)內外齒套的計算。
依據表1、表2具體的參數計算得出內外齒套的齒部基本參數。
3)內外齒套的側隙計算。
當軸線有角位移時 △α=1.6°,鼓形齒與內齒產生相對移動,鼓形齒上各點將相對于 △α=0°時產生位移,此位移在內齒法線上的投影稱為鼓形齒的法向位移量。
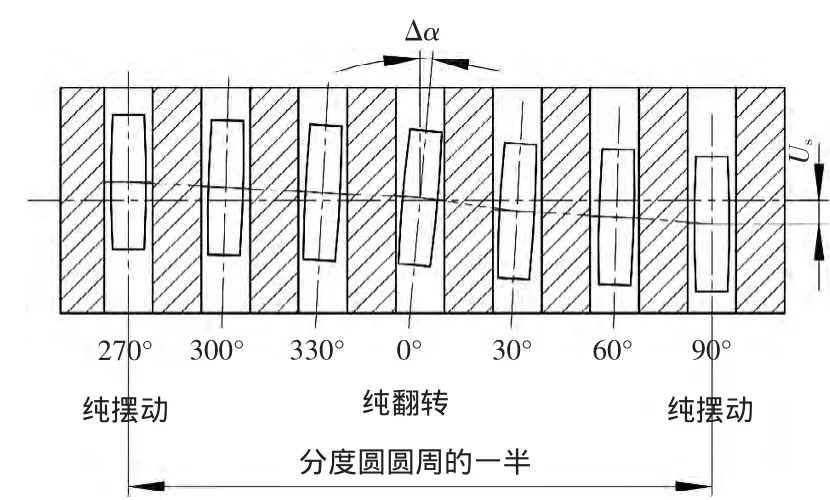
圖4 齒的相對位置
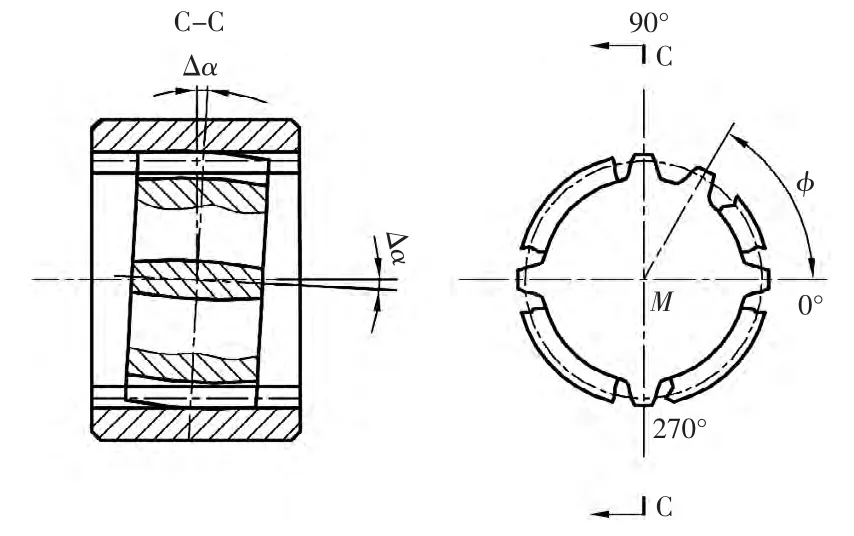
圖5
從圖4、圖5可知,在φ為0°和180°時,鼓形齒為翻轉運動,齒上各點繞齒中心回轉;在90°和270°時,鼓形齒上各點沿齒寬方向偏擺,其余各位置為兩種的合成運動。任意內外齒的左右齒面間的最小法向側隙應同時滿足鼓形齒左右齒面的最大法向位移
而對于內外齒的法向側隙為上述兩者之和:Jnmin=JLmin+JRmin。
在實際設計中我們必須考慮制造誤差對于實際連接的影響。
第一點:見表 3,制造誤差補償量 δn1=[(Fp1+Fp2)cosα+(ff1+ff2)+(Fg+Fβ2)]。式中:Fp1、Fp2為內外齒齒距累積公差;ff1、ff2為內外齒齒形公差;Fg為內齒齒向公差;Fβ2為鼓形齒齒面鼓度的對稱度公差;
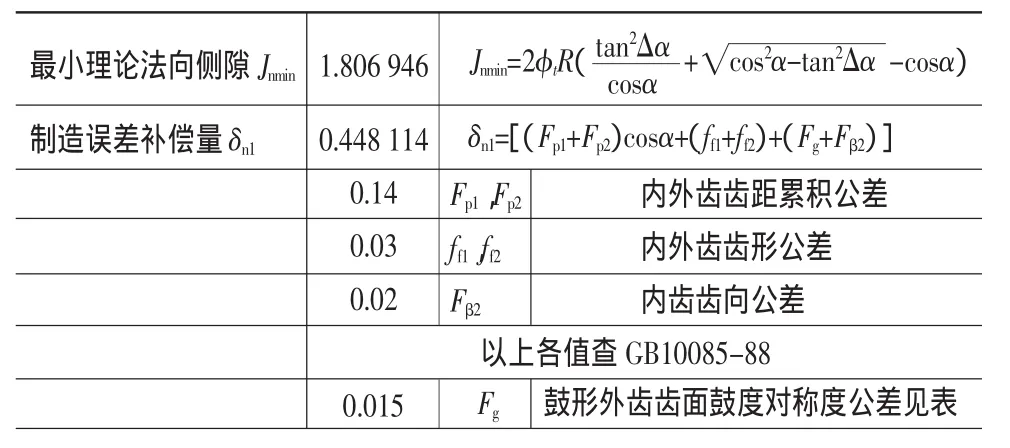
表3
第二點:外齒套與軸過盈連接時齒套膨脹的補償量δn2=△dsinα。式中,△d為外齒套直徑膨脹量,按照過盈連接計算(僅非鍵連接的大過盈配合時考慮)。聯軸器的最小設計法向側隙Jn=Jnmin+δn2+δn1。此項具體數值將在下文中闡述。
2 過盈量的計算
必須對軸和齒套的尺寸公差進行計算,以滿足裝配后達到使用要求。
2.1 彈性變形滿足扭矩要求
材料本身的彈性模量、摩擦因數、兩接觸表面的粗糙度以及具體尺寸。
1)此聯軸器應用中碳合金鋼42CrMo4制造,彈性模量E=206 000 MPa,摩擦因數μ=0.14,軸的表面粗糙度Ra0.8,齒套內孔表面粗糙度Ra1.6,傳遞力矩T=3 780 000 N·m,配合長度lf=520,配合內孔直徑df=600,依據公式Pfmin=2T/(πd2flfμ)可得需要的最小正壓力Pfmin=92 MPa。
2)依據正壓力得出最小直徑變化量emin=PfmindfC/E,得出最小過盈量要求δmin=1.171mm。
3)依據材料和尺寸選擇相應的屈服點σs,抗拉強度σb,通過公式 pfamax=(1=174 MPa和Pfimax==195 MPa獲得包容件和被包容件材料允許的最大結合力。
4)通過材料允許的最大結合力,及公式emax=PfmaxdfC/E得出內外零件最大的膨脹量δemax=eamax+eimax=2.17 mm。
5)初選基本過盈量。依據公式δb=(δmin+δmax)/2=(1.171+2.17)÷2=1.67 mm。
2.2 公差帶的選擇
依據加工工藝和習慣選擇常用公差帶;按照基孔制進行設定H7,因此軸的公差范圍設為+1.64~+1.60 mm,進而得出實際配合公差+1.64~+1.53 mm。
2.3 包容件的膨脹
依據軸和齒套的實際公差范圍為+1.64~+1.53 mm,通過公式P=δE[/(Ci+C)ad]f求得兩個零件接觸表面的正壓力(128.5~120)MPa。依據此壓力按照公式可得齒套外側的徑向膨脹量為1.378~1.285mm。
3 內外齒套齒部參數的設定
通過上面的計算可知外齒套直徑膨脹量為1.378~1.285 mm,依據公式δn2=Δdsinα,得出齒部法向膨脹量為0.471~0.439 mm;因此通過公式 Jn=Jnmin+δn2+δn1,可以得到內外齒套的最小設計法向側隙Jn為2.56~2.53 mm,對于齒形聯軸器一般遵循以下幾點:
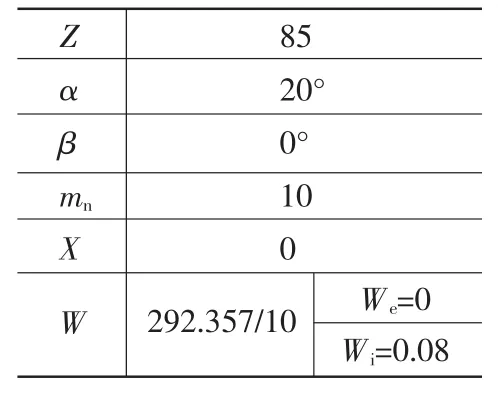
表4
1)外齒套無變位的設計思路進行設計。公法線的偏差依據分度圓尺寸查表得7級精度ΔW=0.08,從而得出具體的參數(見表4);
2)對于內齒套要考慮滿足最小2.56的法向齒側間隙的要求。依據齒輪變位概念,可得內齒圈的變位Xmin=2.56/(2sin20°mn)=0.374,對于公差要求達到8級精度即公法線偏差ΔW=0.115(對于公法線與跨棒距之間的轉換略掉),從而得出具體參數(見表 5);
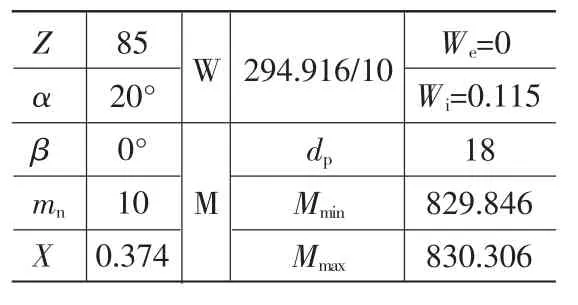
表5 內齒參數
由于軸和外齒套的過盈聯接,將會影響外齒套的外徑變大為:870e8(-0.170-0.310)+(1.285~1.378)即得到的實際最終外齒套的最大齒頂應該在870e8(-0.170-0.310)+1.378。基于聯軸器外徑定心的準則,外齒齒頂執行e8,內齒齒根執行H9的公差配合;故對于內齒的齒根要求為df=871.378H9(-0.2300)。

圖6
4 軸和齒套的安裝問題
保證通過冷、熱處理滿足裝配工藝。碳鋼材料的線性膨脹系數α:加熱時為 11×10-6/℃,冷卻時為-8.5×10-6/℃。依據公式δt=[αa(ta-tg)-αi(titg)]df,按照加熱、冷卻齒套和軸的方式進行處理;加熱320℃,冷卻-40℃;可得齒套與軸產生δt=1.908 mm的間隙,其數值大于零件間的過盈量1.64 mm。如圖6為在實際生產裝配中的圖法,此方案已經生產多臺,在西部高原某水泥廠應用7年以上。
5 結語
對于大扭矩的鼓形齒聯軸器因為實際工藝問題而采用外齒套與軸過盈連接方式,而此種連接方式的外齒套相對較薄,其在裝配到軸上后會有較大的彈性膨脹量以滿足大扭矩的傳輸,而其對于外側齒部參數的影響較大,對于這一點,在內外齒配合時是不可回避的考慮因素。對于過盈連接方式不僅僅應用于鼓形齒聯軸器中,在很多的封閉齒輪箱傳遞中都要應用,因此在薄壁齒輪安裝到軸上進行過盈連接時,其過盈連接對齒部參數的影響也是一個要考慮的點。
[1] 成大先.機械設計手冊:1-2卷[M].北京:化學工業出版社,2008.
[2] 郁明山.齒輪手冊:上冊[M].北京:機械工業出版社,2002.
[3] 趙光發,等.JB/T8854.2001鼓形齒式聯軸器GII CL型、GII CLZ型中華人民共和國機械行業標準[s].北京:中國標準出版社.2001.
[4] 《DRUM COUPLINGS》MALMEDIE TYPE TIX,2002.
[5] 關慧貞,馮辛安.機械制造裝備設計[M].北京:機械工業出版社,2010.

