錨泊系統起錨破土阻力分析

唐文獻，吳文樂，張 建，王筱蓉，孫 澤，李金泰

(1.江蘇科技大學 機械工程學院，江蘇 鎮江 212003；2.江蘇揚遠船舶設備鑄造有限公司，江蘇 泰州 225500)

錨泊系統起錨破土阻力分析

唐文獻1，吳文樂1，張 建1，王筱蓉1，孫 澤2，李金泰1

(1.江蘇科技大學 機械工程學院，江蘇 鎮江 212003；2.江蘇揚遠船舶設備鑄造有限公司，江蘇 泰州 225500)

為提高船舶在起錨過程中的效率與安全性，在經典理論公式基礎上，通過ABAQUS軟件模擬錨泊系統起錨破土過程，建立阻力數值分析方法，得出數值分析結果與土體流動機制。將阻力數值解與理論解進行對比分析。結果表明，數值分析方法比理論公式的結果更加符合預期效果，并且能夠模擬土壤流動情況。

錨泊系統；起錨；ABAQUS；數值分析

錨泊系統是水上漂浮結構物必不可少的部分，能夠在惡劣水域下抵御狂風、巨浪、暴潮，降低危險事故發生的概率。

正常起錨分5個階段：①回收余鏈階段；②收緊錨鏈階段；③錨破土階段；④收起懸錨階段；⑤錨鏈入孔階段。船錨破土是指將部分或全部侵入海床的錨取出的過程，而錨破土過程中的安全性對整個過程具有重要意義。在實際海上作業中，將錨從底質中拔出來的力越小越好，有利于減少船體和錨鏈的載荷，降低船只作業風險。若錨不能及時拔出，將會造成電機堵轉，電流陡增，損壞電機。2014年7月，中國船級社CCS發布了《鋼質海船入級規范修改通報》，對錨操作進行了補充規定，要求提高錨操作時的穩定性[1]。近年來，我國逐步加強對深海油氣資源的開采，為保證海上鉆井平臺工作的穩定性，對錨泊設備提出更高要求，如何提高船舶在錨地起錨過程中的安全性已受到研究人員和相關機構的高度重視。

船舶用錨根據海底土壤不同具有較多種類[2]，本文在理論研究的基礎上，以通用的霍爾錨為對象，采用CEL耦合方法，對船舶在起錨過程中土體的彈塑性變形進行研究，建立起錨破土阻力數值分析方法，所得結果對船舶順利起錨具有重要意義，為船舶在起錨困難時提供破土阻力的計算依據，避免危險事故的發生。

1 起錨破土阻力理論分析

國內外學者對錨破土過程的阻力進行了深入研究，其中具有代表性的有浙江大學于曉杰提出的動摩擦模型理論、Terzaghi理論和ChaoMing Chi理論等，但前兩種理論存在一定的局限性。動摩擦模型理論涉及到土-錨微觀表面剛毛的接觸特性，其參數如錨與土表面剛毛剛度系數等不易得到；Terzaghi理論未考慮錨爪的具體參數，如錨爪長度等[3-5]。因此這兩種理論過于保守，難以指導實際工作。

由于入土錨桿的側摩阻力相對錨爪所受阻力較小，那么在錨卸扣處所受的力就等于在錨爪參考點所受力，ChaoMing Chi綜合考慮了錨和非均質土的影響因素，在Terzaghi等人的基礎上，以恒定速度起錨，從內部耗能的角度研究了錨在參考點所受力的大小[6]。其內部速度能量場與受力情況見圖1。

由圖1可見，錨爪被簡化成AB桿，錨爪抓土后與水平面夾角為θf；α為能量場的剛性楔角。A點附近的內部耗能發生在可變形區域(3)和滑移表面(1)、(2)和(4)。同樣，B點附近的內部耗能發生在可變形區域(7)和滑移表面(5)、(6)和(8)。C點為錨爪重心，也是參考點。

根據彈塑性變形全量理論與Tresca屈服極限推出單位體積內部能耗為

D=Suv0L

(1)

式中：D——內部能耗；Su——不排水抗剪強度；L——滑移表面長度。

那么垂向載荷Fn所產生的能耗就等于總內部能耗：

Fnv0=D1+D2+D3+D4+D5+D6+D7+D8

(2)

因此，垂向載荷為

(3)

由于土體在泥水分界處的不排水抗剪強度不為零，且隨著深度變化逐漸變大，滿足公式[6]：

(4)

式中：k——土壤的強度梯度；z——錨爪的埋深；Su0——泥水分界處的不排水抗剪強度。

起錨拉力主要由錨鏈提供，為豎向載荷。所以，根據式(3)和(4)得破土阻力公式：

(5)

該公式充分考慮了土-錨系統的綜合特性，能夠為錨泊系統起錨破土阻力的預測提供理論基礎。但是實際海況復雜多變，使得計算出的阻力值難以與實際情況完全一致。因此，為了更好地計算出破土阻力，本文在沿用理論公式的基礎上，采用數值分析方法，模擬起錨破土過程，并將理論解與數值解進行對比分析。

2 土-錨系統的有限元數值模型

ABAQUS軟件能夠針對土體的變形與滲流進行耦合分析，滲透定律則采用Forchheimer非線性定律或Darcy定律。為了能夠有效模擬土-錨系統阻力變化，在考慮流固耦合情況下，進行數值模擬計算[7-9]。

2.1 土-錨系統模型

本文研究對象為典型的霍爾錨，最大高度為7.1 m，錨爪高度H為3 m，錨身厚度B為2.2 m，錨爪展開角度α為45°，錨的最大寬度D為5 m。為避免邊界效應，取土體模型寬度L=10D，取深度h=5D，見圖2。

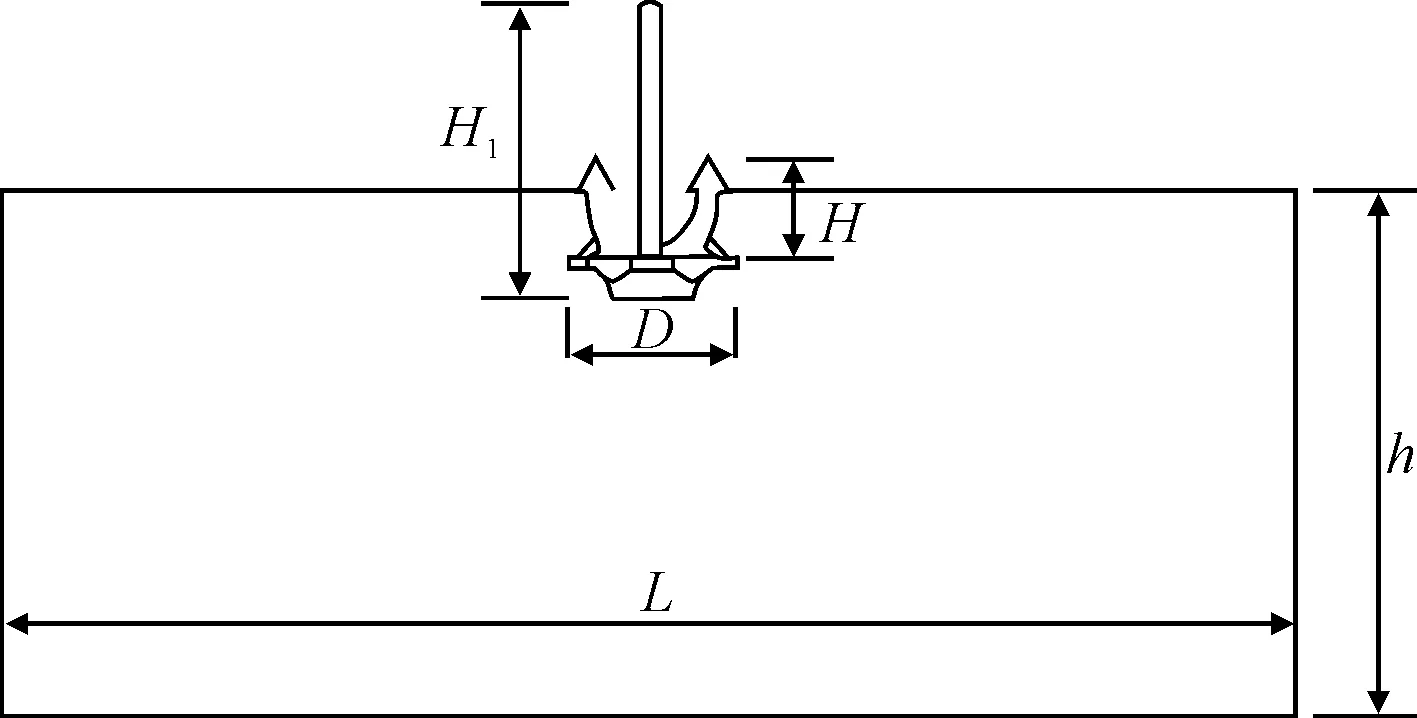
圖2 土-錨系統參數圖

利用ANSA軟件對實體進行網格劃分，霍爾錨網格以六面體縮減積分單元C3D8R為主，局部采用四面體網格離散。由于錨的破土過程為大變形問題，土體的變形程度遠遠比錨的變形程度大得多。因此，在有限元軟件模擬起錨過程中，可以將錨的整體結構設置為剛體，采用恒定速度起錨，加載方式為在船錨卸扣處施加速度邊界條件。

海洋里土層基本是多層土壤構成的交叉狀態，本文將多層土地基簡化成單土地基進行計算。土體網格綜合拉格朗日與歐拉網格的優點，借鑒CEL方法進行分析,選用Mohr-Coulomb模型，將土體單元類型設置為歐拉六面體縮減積分單元EC3D8R[10]。高度主要分為3層：第一層模擬水域，設置為空穴，即無任何材料屬性，空穴深度對計算結果幾乎沒有影響，網格設置最為密集，用來模擬土體在起錨過程中的土體流動及隆起情況；第二層為軟土，破土過程主要發生在該層，為土體的大變形區，對破土阻力影響較大，網格較為密集；第三層與第二層同為軟土，由于對起錨阻力影響較小，為了減小計算時間，網格設置較為稀疏。考慮到土體的自重問題，需要對模型平衡地應力，并設置土體的邊界條件。ABAQUS有限元模型見圖3。

圖3 土-錨系統的有限元模型(隱藏空穴后)

2.2 土-錨系統材料參數

錨材采用鐵質、彈塑性材料，密度ρ=7 900 kg/m3，彈性模量E=200 GPa，泊松比υ=0.3。

土體材料：土體為軟土，彈塑性材料，密度為ρ=1 800 kg/m3，彈性模量E=5.5 MPa，泊松比為v=0.49，內摩擦角φ為10°，初始孔隙比為1，有效容重γ′=7.4 kN/m3，泥水分界處的抗剪強度Su=1.5 kPa，土壤的強度梯度k=1 kPa/m。

2.3 錨的初始埋深

在研究起錨過程時，錨的初始埋深對計算結果存在影響，同時為避免對海底管線和電纜的損壞，需要對船錨的初始埋深進行計算[11]。根據《廣東省沿海航道通航標準》，船舶在應急情況下拋錨的入土深度為2～4 m。一般霍爾錨的入土深度滿足經驗公式：

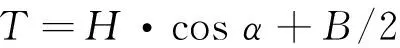
(6)

式中：T——錨的入土深度；H——錨爪的高度；α——錨爪展開角度；B——錨身厚度。

結合本文中使用的霍爾錨模型，錨爪高度H為3 m，錨爪展開角度α為42°，錨爪厚度B為2.2 m，則錨的入土深度為3.3 m，且在《廣東省沿海航道通航標準》范圍之內。

3 起錨破土結果分析與討論

3.1 理論結果分析

由于式(5)中不排水抗剪強度和錨爪抓地夾角為不定值，為了簡化計算，有限元計算中將錨爪抓地夾角設為定值。因此，在理論計算過程中，同樣將夾角設為定值。而對于不排水抗剪強度的影響，主要與埋深有關，在有限元模擬中是以恒定速度起錨，因此埋深隨時間呈線性變化，最終阻力為

(7)

式中：h——錨爪初始深度；v——起錨速度；t——時間變量。

結合數值分析中的數據，經計算得出，破土阻力呈線性變化。

F=142-13.7t

(8)

3.2 數值結果分析

將模型提交計算后，得到一條上下波動但呈下降趨勢的阻力曲線。為方便描述，通過ORIGIN軟件擬合出一條符合實際解的光滑阻力趨勢曲線，見圖4。由圖4可見，以恒定速度起錨時，初始階段船錨位于最深處，起錨阻力最大，下降趨勢較為緩慢；當起錨作業時間到1.5 s左右，船錨上拔至1.5 m處時，阻力下降幅度明顯增大，由于在模型的計算過程中考慮了船錨的自重，因此破土后阻力不會消失。而在實際情況中，當錨完全脫離土壤以后，錨的回收還需克服錨鏈重量以及海流的阻力，這在模型中未予體現。

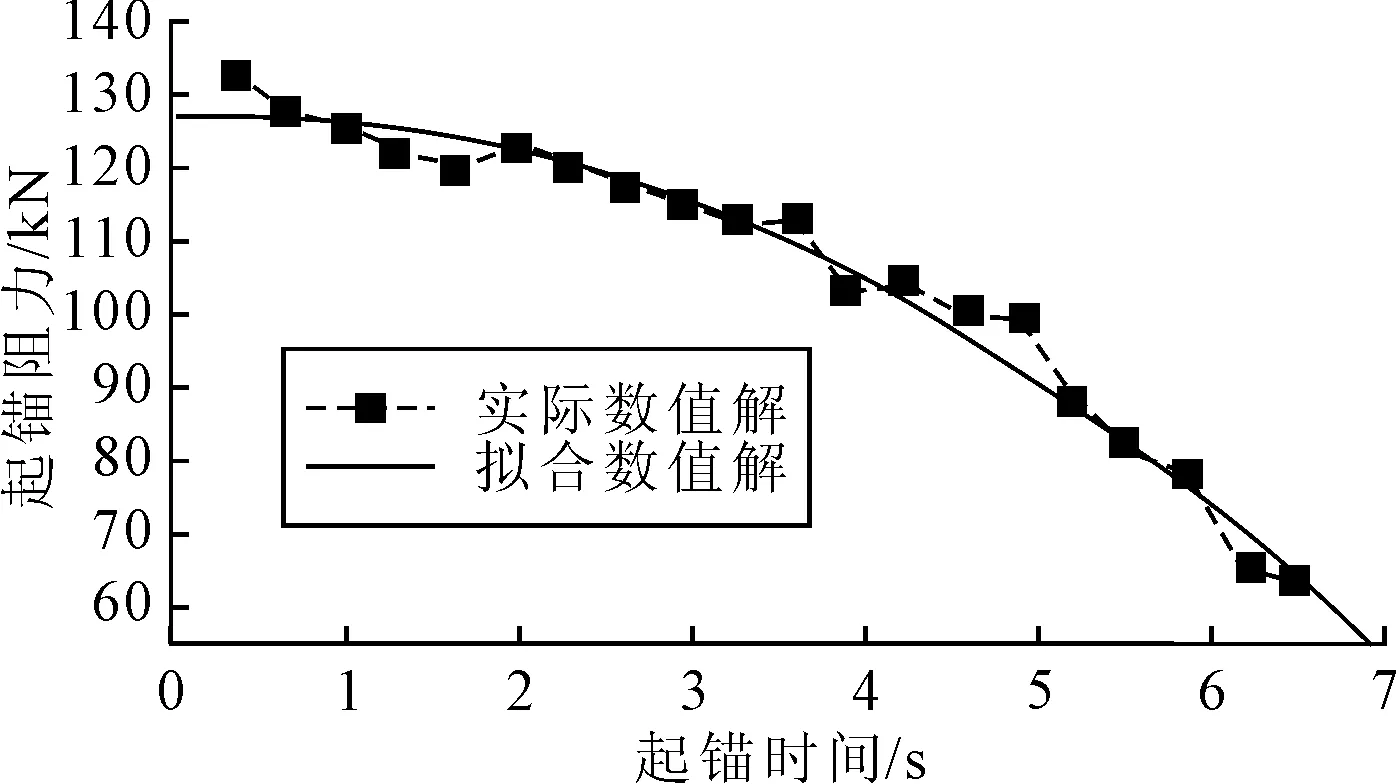
圖4 起錨破土阻力隨深度變化

3.3 理論與數值解對比分析

為了確保結果的準確性，將數值解(擬合出的平滑曲線)與經典理論解進行對比，見圖5。經典理論公式呈線性變化，且在初始階段理論解明顯較大，達到142 kN。這是由于在實際海洋底質中，土體的不排水抗剪強度的變化并非是線性關系，以及在泥水分界處不排水抗剪強度的標準不一。如果想要得到真實的抗剪強度，需進行原位測試或室內試驗，如十字板剪切試驗和三軸剪切試驗等。而對于剛性楔角α，也是基于經驗所得，對結果同樣存在缺陷，因此線性理論解過于保守。而數值解是模擬真實起錨過程，雖然計算原理不同，但是兩者的計算結果也非常接近，因此數值解更加符合實際情況，為錨鏈的強度校核與錨機的動力選擇提供依據，保證船舶海上作業的安全性和穩定性。

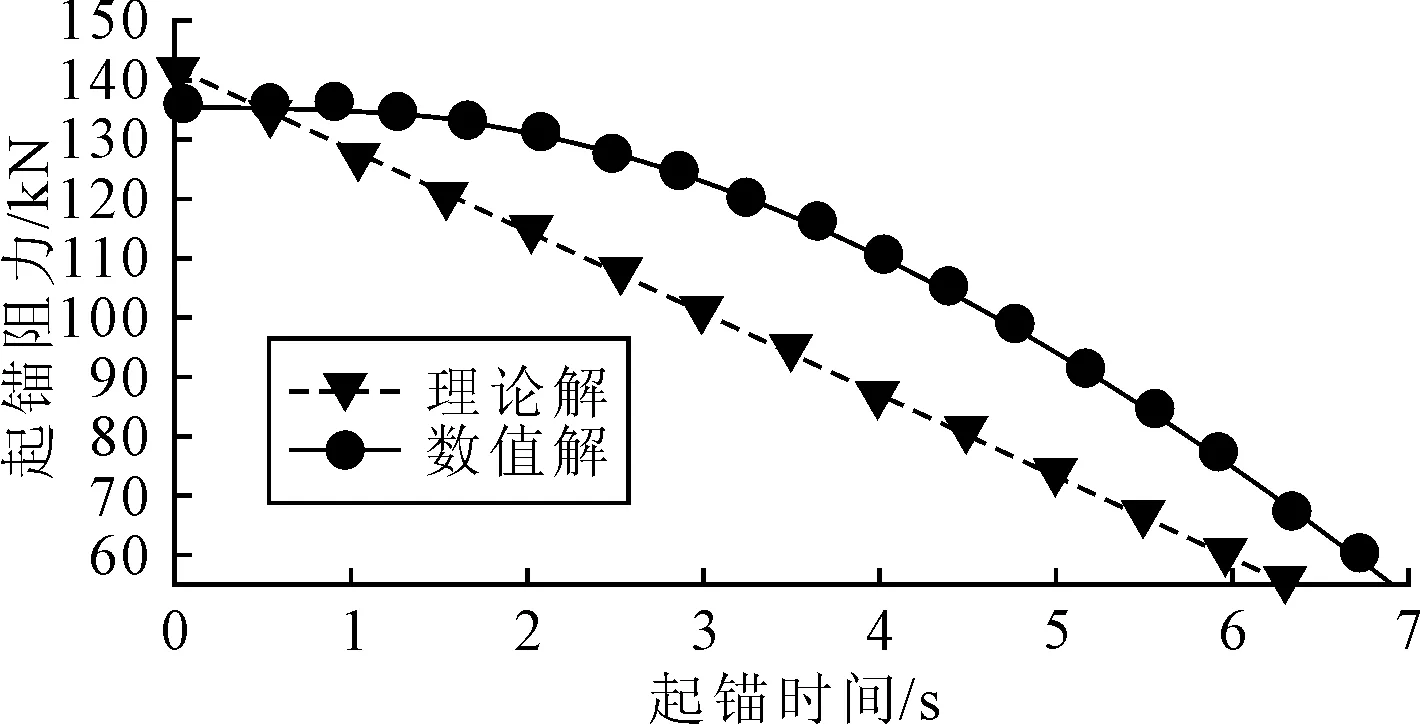
圖5 理論與數值解對比

3.4 起錨土體流動分析

圖6為船舶起錨破土過程中土體的流動情況。上方為水域，無任何材料，用來模擬土壤的隆起情況；下方區域為土體。

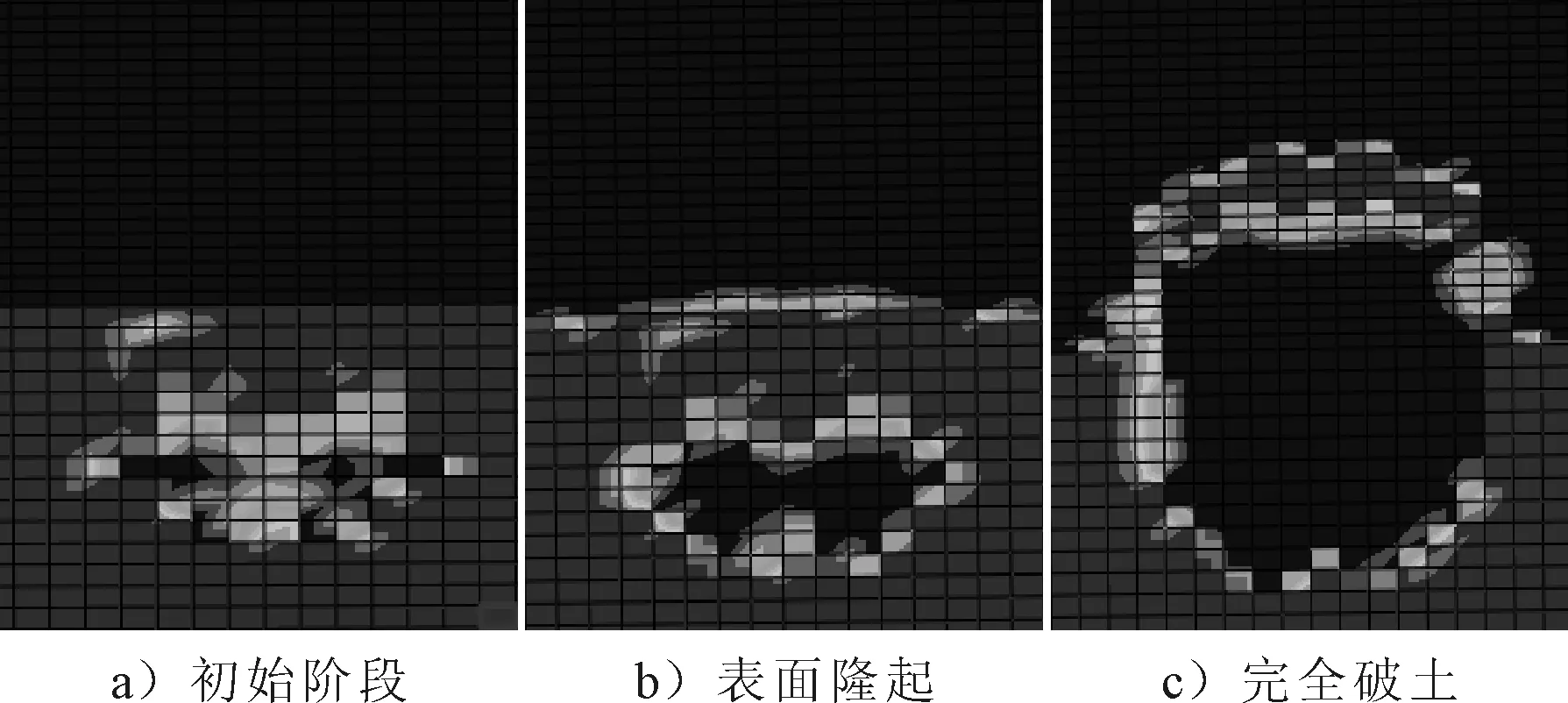
圖6 土體流動示意

由圖6可見，在破土的初始階段，由于土體邊界較廣，此時船錨的埋深最大，起錨只會影響周邊土體，造成剪切破壞，土體開始流動，如圖6a)。而土體隨船錨上拔至一定深度，土體剪切破壞擴展到泥水分界面處，海底表面將會形成隆起，如圖6b)。由于船錨上部存在覆土，因此在上拔的過程中，部分淤泥將會向下流動到船錨底部，造成土體回流，形成一個空腔，同時船錨上部分覆土也會隨著上升一起離開海底層，如圖6c)。因此，數值分析可以充分體現土壤的流動特性，彌補理論公式的缺陷，為進一步研究破土阻力變化提供基礎。

4 結論

1)國內外學者對錨破土的理論研究存在缺陷，ChaoMing Chi理論公式從速度能量場的角度，綜合考慮錨與土的條件參數，推出理論公式，其結果與真實解較為接近。但是完全呈線性變化的不排水抗剪強度與實際不相符，同時破土阻力還受到船錨下方土體水和土體表面水的影響，容易產生誤差，不利于準確預測阻力變化。

2)數值解是以實際情況模擬起錨破土過程，所得結果呈非線性的下降趨勢，能夠較為精確地判斷阻力變化。綜合對比兩種解，其阻力變化趨勢相同，但變化幅度不一。數值解在初始階段變化較為緩慢，而起錨到一定深度時，阻力值急劇下降。與理論值相比，數值解能夠更好地反應船錨在破土過程中的阻力隨深度變化情況，且能夠真實反應土體的流動情況，從而可以保證錨鏈與錨機的正常運作，對船舶海上作業具有重要意義。

[1] 中國船級社.中國鋼質海船入級規范修改通報[S].北京:人民交通出版社,2014.

[2] 葉邦全.海洋工程用錨類型及其發展綜述[J].上海造船，2012(3):1-7.

[3] 于曉杰.淺海工程船移錨作業系統建模分析與仿真技術研究[D].浙江大學,2013.

[4] Canudas De Wit,OLSSON H,ASTROM K J,et all A new model for control of systems with friction[J].Transaction on Automatic Control, 1995,40(3):419-425.

[5] Canudas De Wit,LISCHINSKY P.Adaptive friction compensation with partially known dynamic friction model[J].International Journal of Adaptive Control and Singnal Processing,1997,11:65-80.

[6] CHI ChaoMing,Plastic limit analysis of offshore foundation and anchor[D].Texas A&M University,2010,8.

[7] 丁紅巖,樂叢歡,張浦陽.海上自升式鉆井平臺拔樁階段樁靴上拔阻力的機理研究[J].天津大學學報,2011,44(4):325-330.

[8] SLOAN MERIFIELD R S,S W.The ultimate pullout capacity of anchors in frictional soils[J].Can Geotech J,2006,43(8):852-868.

[9] ZHOU X X,CHOW Y K,LEUNG C F.Numerical modeling of breakout process of objects lying on the seabed surface[J].Computers and Geotechnics,2007,35(5)：686-702.

[10] 王 懿,賈 旭,黃 俊,等.基于CEL的船舶拋錨入泥深度分析[J].石油機械,2014,42(12):44-47.

[11] 譚 箭,李恒志,田 博.關于事故性拋錨對海底管線損害的探討[J].船海工程,2008,37(1):142-144.

Resistance Analysis of Lifting Anchor Ground-breaking Process for Mooring System

TANG Wen-xian1, WU Wen-le1, ZHANG Jian1, WANG Xiao-rong1, SUN Ze2, LI Jin-tai1

(1. School of Mechanical Engineering, Jiangsu University of Science and Technology, Zhenjiang 212003, China;2. Jiangsu Yangyuan Boat and Ship Equipment Casts Co. Ltd., Taizhou Jiangsu 225500, China)

On the basis of classical theoretical formula, the lifting-anchor ground-breaking process of mooring system is simulated by ABAQUS to establish the resistance numerical analysis method. The numerical results and the soil flow mechanisms are obtained. The numerical results of resistance are compared with that of theoretical formulae, showing that the numerical method is more accurate and reasonable.

mooring system; anchor; ABAQUS; numerical analysis

10.3963/j.issn.1671-7953.2015.06.008

2015-09-30

江蘇省自然科學基金項目(BK20150469)

唐文獻(1962-)，男，博士，教授

U664.4

A

1671-7953(2015)06-0031-05

修回日期：2015-10-10

研究方向:海洋工程裝備設計與制造技術

E-mail:tangwenxian@163.com