分組有界變差與幾乎單調遞減的關系

陳曉丹

(浙江理工大學理學院, 杭州 310018)

分組有界變差與幾乎單調遞減的關系

陳曉丹

(浙江理工大學理學院, 杭州 310018)

在Fourier分析中,對一些經典定理單調性的推廣很有意義。探討了分組有界變差與幾乎單調遞減之間的關系;利用數列本身特性,采用構造的方法,給出平凡的數列,并結合三角級數的一致收斂性等相關定理,構造更具有實用價值的數列證明了兩者的互不包含關系。

分組有界變差; 幾乎單調遞減; 互不包含關系

0 引 言

在一致收斂和平均收斂的問題上,三角級數(Fourier)系數的單調遞減條件及其推廣研究是相關研究者關注的焦點。這類研究開始于英國學者Chaundy和Jollife(1916)的工作及Young(1913)的工作,產生了大量優秀的成果[1]。在系數數列集合間的關系中,目前已有很多好的成果,比如擬單調(QM)、剩余有界變差(RBV)等重要概念的引入。Le和Zhou在文獻[2]提出了兼容兩個發展方向(擬單調和有界變差)的分組有界變差(GBV)概念。歷史上還出現過其他一些推廣性的條件,幾乎單調遞減(AMS)就是其中之一。對于擬單調和有界變差這兩個方向的研究已有比較豐富的結果,但關于AMS與各集合之間的關系方面的研究相對較少。

對三角級數的一致收斂方面的研究,目前已經推廣到均值有界變差(MVBV)概念,但出乎意料的是AMS條件卻無法代替經典定理中的單調遞減條件(參見文獻[3])。在Fourier最佳逼近中,AMS與擬幾何遞減條件有一定的關系。因此對AMS的探究可以增強對數列單調性的進一步認識,有助于對各種經典定理進行探索性推廣,為后繼研究者提供方便。本文中我們主要研究AMS與GBVS之間的關系。

1 分組有界變差數列與幾乎單調遞減數列的定義

文獻[3]中已經指出AMS與GBVS之間互不包含,但目前并未給出確切證明。本文主要用構造數列的方法來證明兩者的互不包含關系。

2 定理及其證明

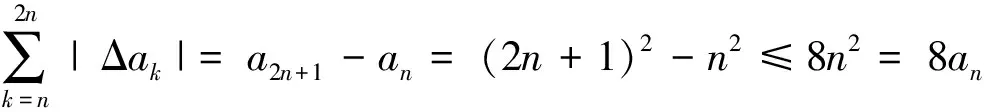
即數列{an}∈GBVS。

假定m≥n,分情況討論:

1)m、n同為偶數時,由于數列am單調遞減,則am≤an。

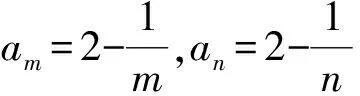
3)m、n為一奇一偶時,

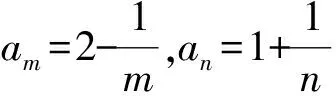
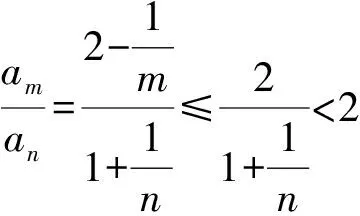
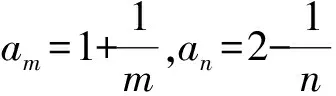
綜上可知,對任意m≥n,都有am≤2an,即數列{an}∈AMS。

但當n為偶數時,有

(n-2)an,

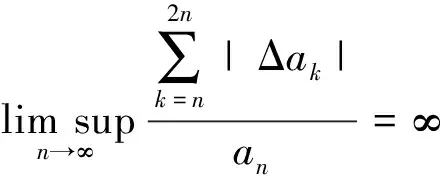
記vm=22m,定義非負數列{bn}:

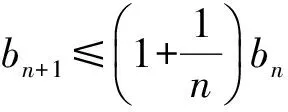
這說明存在數列{bn},滿足{bn}∈GBVS,但{bn}?AMS,即GBVSAMS。

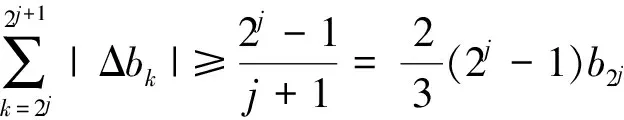
因此,存在數列{bn},使其滿足{bn}∈AMS,但{bn}?GBVS,即AMSGBVS。

由以上兩個例子,定理得以證明。

3 結 語

本文主要通過構造例子說明滿足AMS和GBVS條件之一但不滿足另一條件的數列,從平凡數列及不平凡數列兩方面給出了AMS與GBVS之間互不包含的關系。

[1] Young W H. On the Fourier series of bounded functions[J]. Proc London Math Soc, 1913, 12: 41-70.

[2] Le R J, Zhou S P. A new condition for the uniform convergence of certain trigonometric series[J]. Acta Math. Hungar, 2005, 108: 161-169.

[3] 周頌平. 三角級數研究中的單調性條件: 發展和利用[M]. 北京: 科學出版社, 2012:9-20.

(責任編輯： 康 鋒)

Relationship between Grouped Bound Variation and Almost Monotonic Decreasing

CHENXiao-dan

(School of Sciences, Zhejiang Sci-Tech University, Hangzhou 310018, China)

In Fourier analysis, it is of great significance for the popularization of monotonicity of some classic theorems. This paper discusses the relationship between group bounded variation and almost monotonic decreasing. It makes use of characteristic of series, and adopts construction method to give ordinary series. In addition, it combines with uniform convergence and other relevant theorems of trigonometric series to construct the series with more practical value so as to prove mutual exclusive relationship between them.

group bounded variation; almost monotonic decreasing; mutual exclusive relationship

1673- 3851 (2015) 01- 0146- 03

2014-06-25

陳曉丹(1989-),女,江蘇泰州人,碩士研究生,主要從事逼近論的構造性分析方面的研究。

O174.21

A