流場中沿軸向運動圓柱的附加質量計算

馮雙雙等

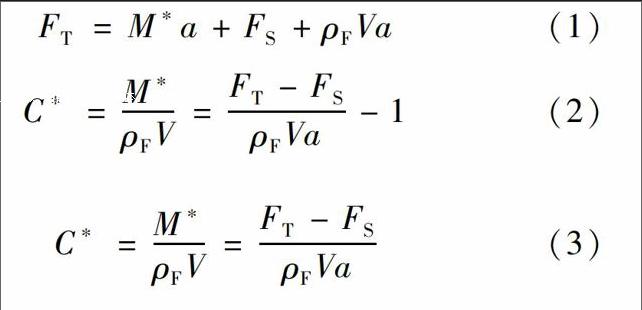
摘要：分別計算理想流體和黏性流體中沿軸向運動圓柱的附加質量.基于相對運動原理得出在無限流體域中不同長細比圓柱的附加質量，驗證附加質量與流體黏性無關的這一結論，并發現長細比越大，附加質量因數越小.利用動網格技術的數值模擬結果表明：圓管中沿軸向運動圓柱的附加質量隨管徑比減小而增大，且流體的流動形態會對物體的附加質量產生一定的影響.以長細比和管徑比為參數給出無限和有限流體域中圓柱附加質量與相應參變量的擬合函數.

關鍵詞：圓柱； 附加質量； 相對運動； 流體黏性； 長細比； 管徑比； 動網格

中圖分類號： O351.2

文獻標志碼：A

Abstract：The added mass of a cylinder moving along its axis in ideal fluid and viscous fluid is calculated. The added mass of the cylinders with different slenderness ratios in infinite fluid domain is calculated on the basis of the principle of relative motion. It is concluded that， the added mass has nothing to do with fluid viscosity， and the larger slender ratio， the smaller added mass factor. The numerical simulation results obtained by moving mesh technique show that， the added mass of the cylinder moving along its axis in tube increases with the decrease of tube diameter ratio， and the flow pattern of fluid has some effect on the added mass. Taking the slenderness ratio and diameter ratio as the parameters， the fitting function of the cylinder in infinite and finite fluid domain with the corresponding variables is given.

Key words：cylinder； added mass； relative motion； fluid viscosity； slenderness ratio； tube diameter ratio； moving mesh

0引言

物體在流體中進行加速運動時，會受到與物體加速度成正比的阻力.這是因為物體會使周圍的流體產生加速度，從而受到流體的反作用力.該阻力與物體的加速度之比即為附加質量，其對于研究流體中物體的運動特性非常關鍵.

早期文獻[1]介紹基于勢流理論在無界域中和固壁附近運動回轉體的附加質量計算方法.20世紀末，隨著計算機技術和硬件設施的快速發展，CFD得到空前開發，并取得一定成就.林超友等[2]采用Hess-Smith方法編制程序計算近海底水下航行體的附加質量；馬燁等[3]利用FLUENT的動網格技術，計算飛艇在6個自由度方向上的附加質量；朱仁傳等[4]和羅敏莉等[5]對船體二維橫剖面繞流進行數值模擬，計算船體的附加質量和阻尼；黃旋等[6]和弓三偉等[7]研究帶空泡彈性物體的附加質量的數值分析方法；傅慧萍等[8]采用動網格技術計算在全黏流體中運動物體的附加質量；周景軍等[9]基于相對運動的思路，在動量方程中添加源項計算水下航行體附加質量.

本文采用CFD軟件CFX，研究流體中沿軸向運動圓柱的附加質量.理論上，流體的黏性對物體的附加質量沒有影響，但在實際中會存在差異，本文分別采用理想流體和黏性流體計算物體的附加質量.首先，基于相對運動原理使來流加速流過靜止的圓柱體，得出在無限流體域中不同長細比圓柱的附加質量，由此探究流體黏性和圓柱的長細比對附加質量因數的影響；然后，利用動網格技術研究在管流中沿圓管軸向運動的圓柱的附加質量，數值模擬結果表明圓柱的附加質量隨管徑比的減小而增大，并進一步揭示理想流體和黏性流體中流場運動形態的差異；最后，根據計算結果給出理想流體域中圓柱附加質量與長細比和管徑比的擬合函數.

1流體中物體附加質量的數值計算

理論分析表明，因物體在流體中加速運動引起的附加質量僅與物體的形狀和周圍流體的密度有關[10]，與物體自身的加速度和流體的黏性無關.根據附加質量與阻力的關系，只要確定物體在加速運動時所受的流體總阻力與定常阻力之差，即可計算出物體的附加質量.

當考察物體在無限流體域中進行定加速運動時，采用相對運動的原理求解其附加質量較為簡單，即認為流體以恒加速度繞流過靜止的物體，相當于整個流體域在作與物體運動反向的加速運動.根據相對性原理，相當于流場受到等效“重力”的作用，其“重力加速度”即為物體運動的加速度.按此方法計算出流體總阻力

根據式（1），分別采用密度為1 kg/m3的理想流體和黏性流體進行計算.設置無限流體域的邊界條件：入口處的均勻來流以Vx=0.1t m/s規律線性變化，即物體的加速度為0.1 m/s2；流域的出口設定為開放邊界.當流體為理想流體時，流體沿壁面可以相對滑動[10]，故側面邊界和圓柱壁面均為自由滑移邊界；采用黏性動力系數為10-6

Pa·s的流體時，考慮無限流體域不計邊界尺寸的影響，設置側面邊界為自由滑移邊界，圓柱壁面為無滑移壁面.采用層流

模型進行分析.時間離散均采用2階向后歐拉差分格式，總時間為0.060 s，計算時間步長為0.002 s.

以β=1的模型為例，圓柱總阻力時程曲線見圖3.理想流體在對應的每個時間步計算相應的定常阻力值為0，與理論計算一致.[10]由式（2）計算理想流體中t=0.060 s時圓柱的附加質量因數為0.501 1.當流體為黏性流體時，計算t=0.060 s時圓柱所受的定常阻力為

3.708 03×10-6 N，修正后的附加質量因數為0.501 3.數值計算得到不同長細比圓柱的附加質量因數，見表1.

β=1時圓柱變為圓球，其在無限流體域中的附加質量因數理論解為0.5，由表1可知，計算誤差在1%以內，表明此方法具有較高的精度.由圖3可知，圓柱在理想流體和黏性流體中總阻力的收斂情況差異不大，在最初幾個時間步有較大的波動，隨后都收斂為一個穩定的值，由此得到的圓柱附加質量差異較小，驗證物體的附加質量與流體的黏性無關這一結論.表1中圓柱的附加質量因數隨β的增大而相應減小，可認為當β足夠大時，附加質量因數的值很小，相應的慣性阻力作用的影響也很小.

為探究β與附加質量的關系，且根據附加質量與流體黏性無關的結論，由表1的數據擬合理想流體中圓柱附加質量因數C*與β的變化關系，即

3有限流體域中圓柱的附加質量

物體在有限流體域（管流）中進行變速運動時，由于圓管邊界到圓柱壁面的距離較近，在無限流體域中均勻來流繞過靜止圓柱的情況不再適用，故采用動網格技術模擬物體運動，使周圍的靜止流體跟隨物體一起運動.圓柱沿軸向進行定加速運動時，計算域前后兩端尺寸的影響較大，因此將圖1中的尺寸擴大為L1=L2=150d，圓柱的兩端仍分別放置2個d=1 m的半球體，L=6 m.

為研究在有限域中固壁邊界距離對物體附加質量的影響，以圓管直徑與圓柱直徑比即管徑比α=Dt/dm分別為5.0，2.0，1.5，1.4，1.3，1.2和1.1等7種情況建立模型，計算圓柱的附加質量，其中Dt為圓管直徑，dm為圓柱直徑.

仍采用單位密度的理想流體和黏性流體，采用動網格技術模擬圓柱在靜止管流中的運動，加速度為0.01 m/s2.圓管出入口邊界均設置為網格靜止的開放邊界.對于理想流體，圓管壁面設定為網格靜止的自由滑移壁面，圓柱壁面為指定網格位移Dx=0.5at2的自由滑移壁面；對于黏性流體，圓管壁面設定為網格靜止的固壁面，圓柱壁面為無滑移壁面，并指定網格位移Dx=0.5at2，湍流模型采用SST模型.計算均采用2階向后歐拉差分格式進行時域積分，總時間為1 s，時間步長為0.05 s.

以α=1.1的計算模型為例，對其數值結果進行分析.圓柱總阻力時程曲線見圖5.理想流體中的黏性阻力為0，由式（3）計算得到t=1 s時圓柱的附

加質量因數C=4.140 2.流體為黏性流體時，計算t=1.00 s時刻圓柱所受的定常阻力，包括黏性阻力和壓差阻力.對流場進行穩態分析，繪制其對稱面上圓柱尾部流場的流線（見圖6a），觀察到圓柱尾部的流場有漩渦產生，流體發生嚴重分離，此時定常阻力值較大，為0.001 642 66 N，扣除定常阻力值，由式（3）計算得到圓柱的附加質量因數C=4.124 3.α取其他不同值時黏性流體中圓柱尾部的流場形態見圖6，附加質量因數C的計算值見表2.

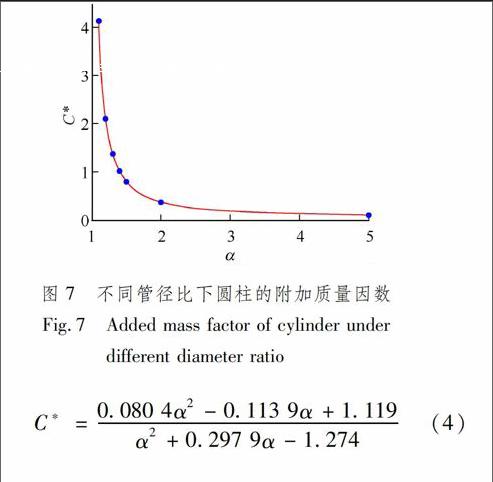
由表2可知，圓柱的附加質量隨α的減小快速增大，這是由于固壁邊界限制圓柱前部的流體向側向運動，使得圓柱需要推動前方更多的流體進行加速運動，從而引起附加質量的增大.表中的數據顯示，α=1.1時黏性流體中圓柱的附加質量因數偏小，推斷是由于黏性流體中圓柱尾部流場發生嚴重分離，圓柱運動時帶動的流體質量減少.由圖6可知，在有界域中理想流體和黏性流體流場的流動形態差異較大，黏性流體中圓柱尾部易產生漩渦，發生嚴重的流體分離現象，故黏性流中圓柱所受的定常阻力值較大，但隨著α的增大，圓柱末端有漩渦的尾流運動逐漸減弱.由表2擬合理想流體中附加質量因數C與α的變化函數，繪制相應的擬合曲線，見圖7.

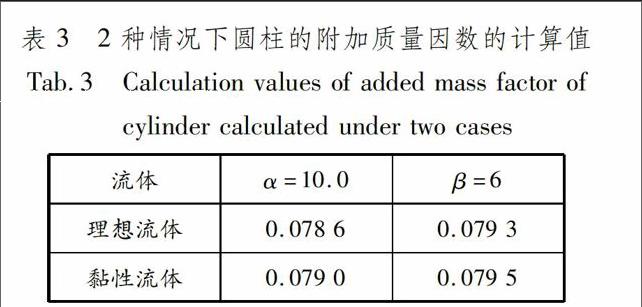
比較表3中的數據可知，利用動網格技術計算得到的附加質量因數與基于相對運動原理計算得到的附加質量因數差異較小，驗證動網格技術計算結果的可靠性.

4結論

通過建立一系列計算模型，得出在不同邊界條件下不同尺寸圓柱的附加質量，結論如下.

1）基于相對運動的原理，在無限流體域中可采用均勻來流繞流靜止圓柱的方法精確地計算不同長細比圓柱的附加質量，且長細比越大圓柱的附加質量因數越小，驗證在無限流體域中圓柱的附加質量因數與流體黏性無關這一結論.

2）采用動網格技術模擬圓柱在不同直徑的圓管中進行定加速運動的情況，得知隨著圓管直徑的減小，圓柱的附加質量快速地增大，意味著圓柱要推動更多的流體作加速運動.

3）在有限黏性流體域中，圓柱尾部的流體發生嚴重分離，形成有漩渦運動的尾流，使圓柱受到較大的壓差阻力.

4）理論認為物體的附加質量與流體的黏性無關，但在有限流體域中，理想流體與黏性流體的流場形態有較大的差異，對物體的附加質量有一定影響.

5）給出圓柱的附加質量因數與長細比及管徑比的函數關系，具有很大的應用價值.

參考文獻：

[1]許維德， 林建國. 細長回轉體附加質量的數值計算[J]. 水動力學研究與進展， 1986， 1（2）：70-81.

XU Weide， LIN Jianguo. Numerical calculation of added masses of slender bodies of revolution[J]. Adv Hydrodynamics， 1986， 1（2）： 70-81.

[2]林超友， 朱軍. 潛艇近海底航行附加質量數值計算[J]. 船舶工程， 2003， 25（1）： 26-29.

LIN Chaoyou， ZHU Jun. Numerical computation of added mass of submarine maneuvering with small clearance to sea-bottom[J]. Ship Eng， 2003， 25（1）： 26-29.

[3]馬燁， 單雪雄. 數值計算復雜外形物體附加質量的新方法[J]. 計算機仿真， 2007， 24（5）： 75-78.

MA Ye， SHAN Xuexiong. A new numerical computation method for added masses of complicated object[J]. Comput Simulation， 2007， 24（5）： 75-78

[4]朱仁傳， 郭海強， 繆國平， 等. 一種基于CFD理論船舶附加質量與阻尼的計算方法[J]. 上海交通大學學報， 2009， 43（2）： 198-203.

ZHU Renchuan， GUO Haiqiang， MIAO Guoping， et al. A computational method for evaluation of added mass and damping of ship based on CFD theory[J]. J Shanhai Jiaotong Univ， 2009， 43（2）： 198-203.

[5]羅敏莉， 毛筱菲， 王曉俠. 強迫運動柱體附加質量與阻尼系數的CFD計算[J]. 水動力學研究與進展： A輯， 2011， 26（4）： 509-514.

LUO Minli， MAO Xiaofei， WANG Xiaoxia. CFD-based added mass and damping coefficients calculation to forced motion cylinder[J]. Chin J Hydrodynamics： A， 2011， 26（4）： 509-514.

[6]黃旋， 魯傳敬， 李杰. 帶空泡運動航行體的附加質量研究[J]. 水動力學研究與進展： A輯， 2009， 24（6）： 800-806.

HUANG Xun， LU Chuanjing， LI Jie. Research on added mass of a cavity running vehicle[J]. Chin J Hydrodynamics： A， 2009， 24（6）： 800-806.

[7]弓三偉， 陸宏志， 鄒正平， 等. 彈性體和帶空泡體的附加質量動態數值計算[J]. 計算機仿真， 2010， 27（4）： 349-353.

GONG Sanwei， LU Hongzhi， ZOU Zhengping， et al. Hydrodynamic numerical computation of the added mass of elastic body & cavitation bubble[J]. Comput Simulation， 2010， 27（4）： 349-353.

[8]傅慧萍， 李杰. 附加質量CFD計算方法研究[J]. 哈爾濱工程大學報， 2011， 32（2）： 148-152.

FU Huiping， LI Jie. Numerical studies of added mass based on CFD method[J]. J Harbin Eng Univ， 2011， 32（2）： 148-152.

[9]周景軍， 李育英， 項慶睿. 一種水下航行體附加質量數值計算方法[J]. 魚雷技術， 2013， 21（4）： 246-249.

ZHOU Jingjun， LI Yuying， XIANG Qingrui. A numerical computation method of additional mass for underwater vehicle[J]. Torpedo Technol， 2013， 21（4）： 246-249.

[10]茅春浦. 流體力學[M]. 上海： 上海交通大學出版社， 1995： 340-353.

（編輯武曉英）