上覆分數階粘彈性飽和場地土位移地震放大系數
劉林超,閆啟方,劉 滕
(信陽師范學院 土木工程學院,河南 信陽 464000)
上覆分數階粘彈性飽和場地土位移地震放大系數
劉林超,閆啟方,劉 滕
(信陽師范學院 土木工程學院,河南 信陽 464000)
考慮土體液相和固相的耦合作用,將基巖上覆場地土視為兩相飽和多孔介質。為了考慮飽和場地土的粘彈性特性,其固相土骨架的應力應變關系利用分數階Kelvin粘彈性模型來描述,建立了上覆分數階粘彈性飽和場地土在簡諧地震波作用下的運動控制方程。運用分數導數的性質并考慮上覆場地土的邊界條件和透水性條件求解了上覆分數階粘彈性場地土在簡諧地震波作用下的振動問題,得到了飽和場地土的位移地震放大系數。采用數值算例分析討論了分數導數的階數、液固耦合系數、土體模型參數、基巖土體剪切模量比等參數對位移地震放大系數的影響。研究結果表明,分數導數的階數、液固耦合系數、土體模型參數、基巖土體剪切模量比對飽和場地土的地震響應有較大的影響,通過壓實場地土,可以達到增大液固耦合系數減小地震響應的作用,通過增大飽和場地土的粘性和剪切模量也可以減小地震反應。
飽和土;分數導數;地震波;地震放大系數;液固耦合系數
地震往往會造成建筑物和人員的傷亡,在進行建筑抗震設計時要選擇有利的建筑場地,這是因為不同的場地條件和場地土的動力學特性對地震的放大效應不同,且十分敏感。因此,研究不同場地條件下場地土的振動特性和地震反應成為地震和巖土工程領域研究的一個重點和難點,且受到了該領域專家的足夠重視。從20世紀60年代開始,不少學者就采用各種模型、方法對地震激勵作用下場地土的動力學特性進行了研究,Idriss等[1]在一維剪切梁模型的基礎上研究了剪切模量為常數和沿深度按冪函數變化的場地土的動力特性和地震反應;Wolf[2]將土層簡化為豎桿,研究了剪切模量按指數函數隨深度增大的勻質自由場地土層的豎向振動;Zhao[3-4]對剪切模量沿深度按冪函數分布的場地土進行了地面振動分析和橫向振動研究;高玉峰[5]在時間域內給出了基巖任意輸入地震作用下一維土層地震反應的解析解;欒茂田等[6]基于一維剪切梁模型,運用分離變量方法研究了各層土的剪切模量沿深度按冪函數規律變化的水平成層非均質地基的自振特性和地震動力反應。尚守平等[7]基于一維波動模型,假設土層剪切模量沿深度按指數規律增長,研究了基巖上作用豎直向上傳播的穩態剪切地震波激振的場地土的橫向自由振動。Chen等[8]在凍融情況下研究了土層的地震反應。Nimtaj等[9]利用時域-頻域混合方法研究了土層的非線性地震反應。這些研究對研究場地土的動態特性起到了重要作用。然而,由于實際工程中土體是由固液氣組成的三相多孔介質,且具有粘彈性性質,將其視為單相彈性介質勢必與工程實際不符。考慮土體的粘彈性特性,李剛等[10]采用工程波動理論,考慮簡諧SH波誘發的水平振動和場地土的材料阻尼,假定場地土體系處于反平面應變狀態,研究半空間上SH波激勵下上覆粘彈性場地土的自由場動力反應;劉林超等[11]借助于一維波動模型和分數導數粘彈性本構關系,分析了在豎直向上傳播的剪切地震波激勵作用下,基巖上分數導數粘彈性場地土的橫向振動問題;段瑋瑋等[12]基于Biot飽和土理論和分數階導數理論研究了飽和分數導數型粘彈性土層的豎向振動放大效應。為了考慮液相的影響,筆者基于飽和土的多孔介質理論,將基巖上覆土體視為兩相飽和多孔介質,利用分數導數粘彈性模型描述固相土骨架的應力應變關系,研究簡諧地震波作用下上覆分數階粘彈性飽和場地土的地震反應與振動特性。
1 模型與控制方程

(1)
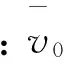
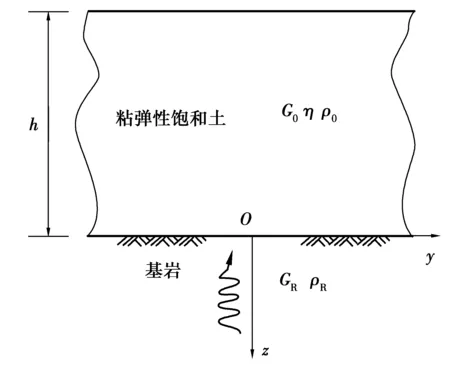
圖1 基巖上覆分數導數粘彈性飽和場地土Fig.1 Fractional derivative viscoelastic saturated site soil on a bedrock
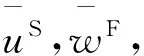
(2)
(3)
(4)
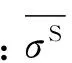
為了更加合理的考慮上覆飽和場地土的粘彈性特性,采用分數階Kelvin粘彈性本構模型來描述固相土骨架的應力-位移關系,即[14]
(5)
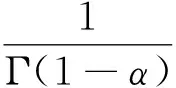
將式(5)代入式(1),可得簡諧地震波作用下上覆分數階粘彈性飽和場地土的運動控制方程為
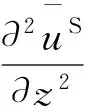
(6)
(7)
(8)
2 簡諧地震波作用下上覆分數階粘彈性飽和場地土振動求解
(9)
(10)
(11)
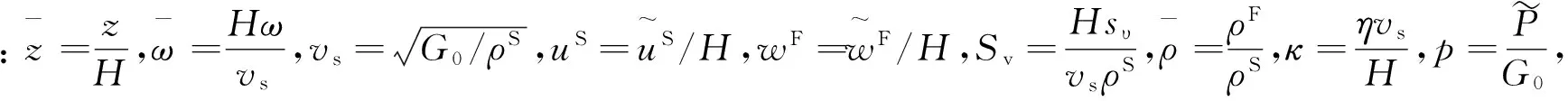
(12)
(13)
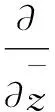
(14)
將式(13)代入式(12)整理得
(15)
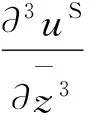
(16)
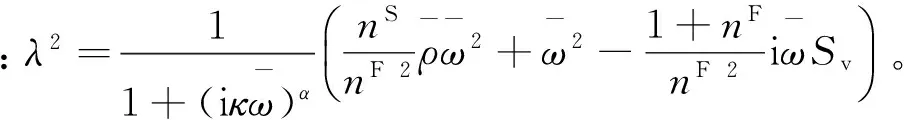
求解式(16)有
(17)
由式(13)、(16)、(17)可得
(18)
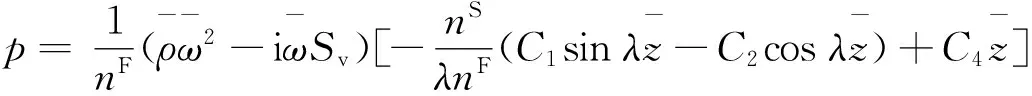
(19)
式(17)、(18)、(19)中,C1、C2、C3、C4、C5為待定系數,可以從邊界條件得到。
3 上覆分數階粘彈性飽和場地土的位移地震放大系數
將基巖看作彈性體,由基巖的入射地震波位移表達式(1)和基巖剪力與位移的關系可知地震波產生的基巖剪應力幅值為
(20)
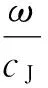
(21)

C1+C3=v0
(22)
(23)
(24)
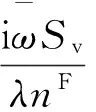
(25)
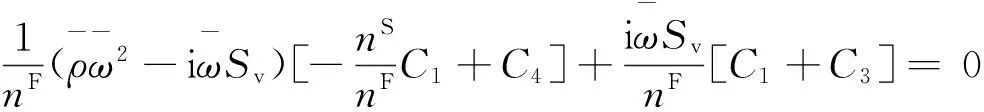
(26)
求解式(22)~(26)可得
C1=a1v0,C2=a2v0,C3=a3v0,
C4=a4v0,C5=a5v0
(27)
式中:
(28)
由式(17)可得固相土骨架的位移為
(29)
引入分數導數粘彈性飽和場地土的地震位移放大系數[9]
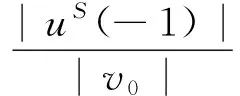
(30)
4 位移地震放大系數分析與討論
針對由式(30)得到的上覆分數階粘彈性飽和場地土地震位移放大系數,采用數值算例的形式來分析討論分數導數的階數α、液固耦合系數Sv、土體模型參數κ、基巖土體剪切模量比GJ/G0對地震位移放大系數的影響。在未作說明的情況下,有關參數的取值為α=0.5、nS=0.67、nF=0.33、Sv=0.5、κ=0.8、GJ/G0=1 000、ρJ/ρ0=2。圖2~6為上覆分數階粘彈性飽和場地土地震位移放大系數隨無量綱頻率的變化曲線。很明顯,曲線存在著波峰和波谷,也就是說,在簡諧地震波作用下,系統將產生共振現象。分數導數的階數α對地震位移放大系數的影響見圖2和圖3,隨著分數導數的階數α的增大,上覆分數階粘彈性飽和場地土地震位移放大系數將減小,且逐漸退化到經典粘彈性飽和土的情形。由圖1、圖2和圖3可以看出,飽和土液固耦合系數Sv對上覆分數階粘彈性飽和場地土地震位移放大系數的影響相當明顯(圖4)。當液固耦合系數Sv較小時,地震位移放大系數隨頻率變化曲線的峰值越大且越尖,隨著液固耦合系數Sv的增大,地震位移放大系數隨頻率變化曲線的峰值將明顯減小。可見,在實際工程中,對飽和的軟土需要進行輾壓,這樣將使其液固耦合系數增大,從而減小其地震反應。隨著飽和場地土土體模型參數κ(即粘性)的增長,場地土的耗散地震能量的能力將增大,此時,地震位移放大系數將減小(圖5)。基巖土體剪切模量比GJ/G0對地震位移放大系數的影響見圖6,隨著基巖土體剪切模量比GJ/G0的減小,也即土體剪切模量G0的增大,地震位移放大系數減小,這是因為土體剪切模量越大,相應的剪應力將增大,可見在實際工程中提高基巖上覆土的剪切模量對提高地基的抗震性能有利。
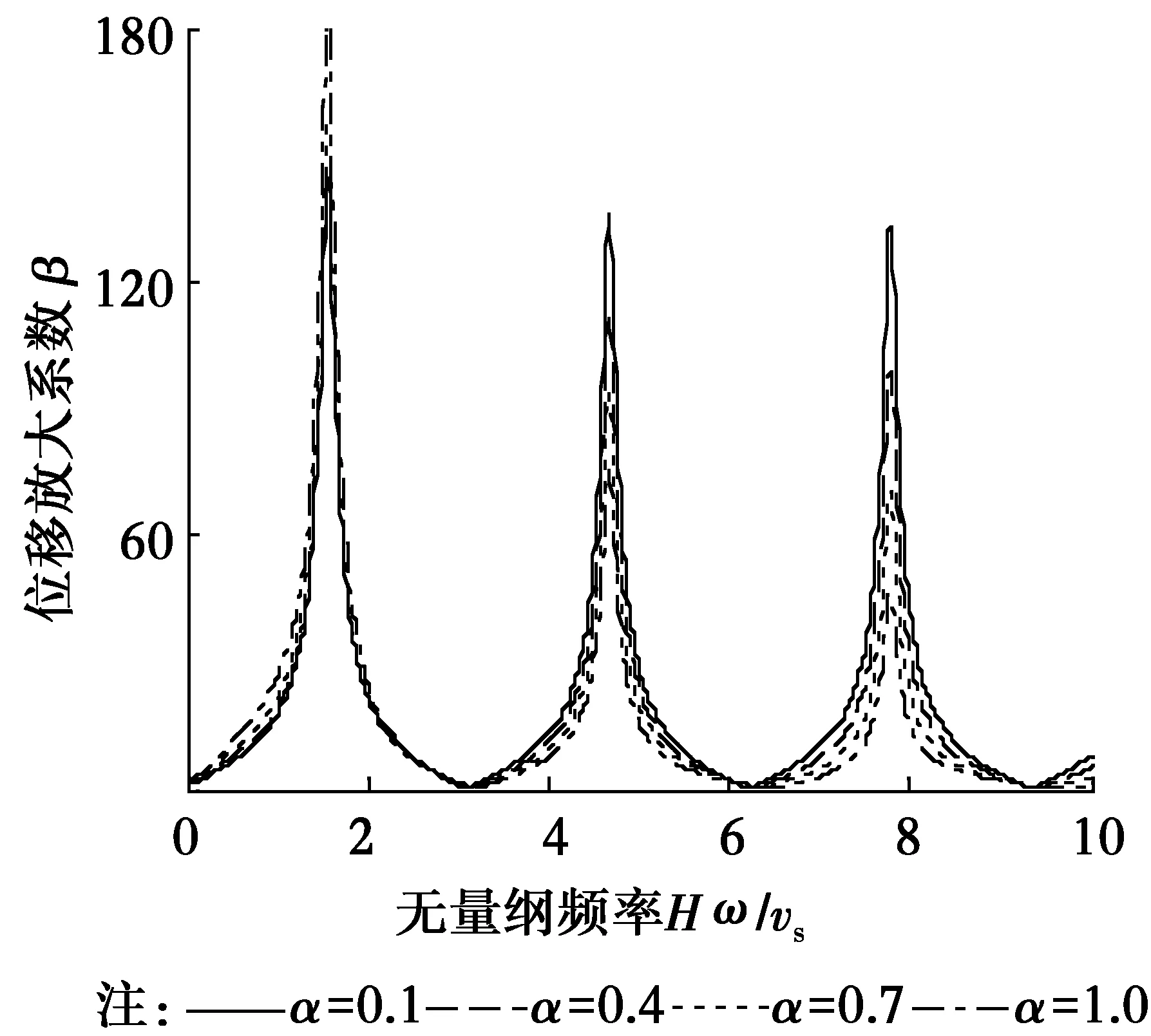
圖2 分數導數的階數α對位移地震放大系數的影響(Sv=0.05)Fig.2 The influence of the order of fractional derivative on displacement seismic amplification coefficient

圖3 分數導數的階數α對位移地震放大系數的影響(Sv=0.5)Fig.3 The influence of the order of fractional derivative on displacement seismic amplification coefficient
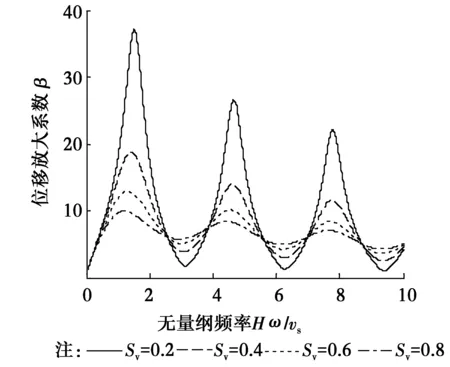
圖4 液固耦合系數Sv對位移地震放大系數的影響Fig.4 The influence of fluid and solid coupling coefficient on displacement seismic amplification coefficient

圖5 土體模型參數κ對位移地震放大系數的影響Fig.5 The influence of soil model parameter on displacement seismic amplification coefficient
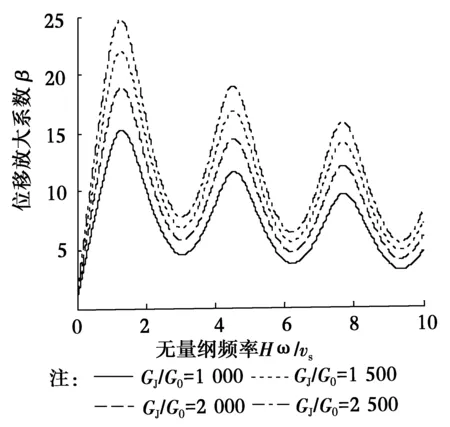
圖6 基巖土體剪切模量比GJ/G0對位移地震放大系數的影響Fig.6 The influence of shear modulus ratio of rock and soil on displacement seismic amplification coefficient
5 結 論
為了使對基巖上覆場地土動力特性的研究更加符合工程實際,必須要考慮液相影響和土體的粘彈性特性。筆者在飽和土理論、粘彈性理論、分數導數理論等理論的基礎上,研究了上覆分數階粘彈性飽和場地土的地震位移響應。與將上覆土視為單相彈性介質一樣,上覆分數階粘彈性飽和場地土在簡諧地震激勵的作用下同樣存在有共振現象。通過分析發現,飽和土的液固耦合系數和土體模型參數對場地土的地震位移放大系數有較大的影響,可見,忽略液相和固相的影響以及土體的粘性來研究場地土的地震響應問題將與工程實際存在差異。為了降低地震造成的地震響應放大效應的影響,需要對場地土進行壓實,達到增大液固耦合系數和土體剪切模量進而減小地震響應的目的。
[1] Idriss I M,Seed H B. Seismic response of horizontal soillayers [J]. Journal of the Soil Mechanics and Foundations Division,ASCE,1968,94(SM4): 1003-1031.
[2] Wolf J P.土-結構動力相互作用[M].吳世明. 譯.北京:地震出版社,1989. Wolf J P. Dynamic soil-structure interaction [M]. Wu S M. Beijing: Seismic Press,1989. (in Chinese)
[3] Zhao J X. Estimating modal parameters for a simple soft-soil site having a linear distribution of shear wave velocity with depth [J].Earthquake Engineering and Structure Dynamics,1996,25(2): 163-178.
[4] Zhao J X. Modal analysis of soft-soil sites including radiationdamping [J].Earthquake Engineering and Structure Dynamics,1997,26(l):93-113.
[5] 高玉峰.成層地基一維土層地震反應解析解[J].巖土工程學報,1999,21(4):498-500. Gao Y F. General solution to the soil seismic response stratified foundations [J]. Chinese Journal of Geotechnical Engineering,1999,21(4): 498-500. (in Chinese)
[6] 欒茂田,劉占閣. 成層場地振動特性及地震反應簡化解析解的完整形式[J].巖土工程學報,2003,25(6):747-749. Luan M T,Liu Z G. A complete form of simplified analytical solution of natural vibration characteristics and seismic response of horizontally-layered soil sites [J]. Chinese Journal of Geotechnical Engineering,2003,25(6):747-749. (in Chinese)
[7] 尚守平,李剛,任慧.剪切模量沿深度按指數規律增大的場地土的地震放大效應[J].工程力學,2005,22(5): 155- 157. Shang S P,Li G,Ren H. Seimic amplification of sites with exponentially increasing shear modulus with depth [J]. Engineering Mechanics,2005,22(5): 155-157. (in Chinese)
[8] Chen Z S,Meng S J,Li Y R,et al. A study on the analysis method of soil layer seismic response in seasonal frozen site [J]. Applied Mechanics and Materials,2012,238: 872-875.
[9] Nimtaj A,Bagheripour M H. Non-linear seismic response analysis of the layered soil deposit using hybrid frequency-time domain (HFTD) approach [J]. European Journal of Environmental and Engineering,2013,17(10): 1039-1056.
[10] 李剛,段林,熊益農,等.SH波激勵下上覆粘彈性場地土的振動分析[J].中南公路工程,2007,32(2): 91-94. Li G,Duan L,Xiong Y N,et al. Vibration analysis of overlying viscoelastic soil layer under SH wave excitation [J]. Central South Highway Engineering,2007,32(2): 91-94. (in Chinese)
[11] 劉林超,高洪波,閆啟方.上覆分數導數粘彈性場地土地震放大效應[J].應用力學學報,2010,27(4):646-649. Liu L C,Gao H B,Yan Q F. Seismic response analysis of amplification of ground soil by fractional derivative viscoelastic model [J]. Chinese Journal of Applied Mechanics,2010,27(4): 646-649. (in Chinese)
[12] 段瑋瑋,聞敏杰,李強.飽和分數導數型粘彈性土層豎向振動放大效應[J].工程力學,2013,30(4):235-240. Duan W W,Wen M J,Li Q. Vertical vibration amplication of a saturated fractional derivative type viscoelastic soil layer [J]. Engineering Mechanics,2013,30(4): 235-240. (in Chinese)
[13] 劉林超,閆啟方.飽和土中管樁的水平動阻抗研究[J].巖土力學,2014,35(5):1348-1356. Liu L C,Yan Q F. Study of lateral dynamic impedance of pipe pile in saturated soil [J]. Rock and Soil Mechanics,2014,35(5): 1348-1356. (in Chinese)
[14] 劉林超,閆啟方.一維分數導數粘彈性飽和多孔介質層的穩態響應[J].工程力學,2012,29(3):41-44. Liu L C,Yan Q F. Stedy state response of one- dimension liquid-saturated porous medium using fractional derivative viscoelastic model [J]. Engineering Mechanics,2012,29(3): 41-44. (in Chinese)
[15] Podlubny I. Fractional differential equation: An introduction to fractional derivatives,fractional differential equations,some methods of their solution and some of their applications [M]. Academic Press,San Diego,1999.
(編輯 胡英奎)
Displacement seismic amplification coefficient of overlying fractional derivative viscoelastic saturated site soil
LiuLinchao,YanQifang,LiuTeng
(School of Civil Engineering,Xinyang Normal University,Xinyang 464000,Henan,P. R. China)
Considering the coupling effect between fluid phase and solid phase,the site soil on bedrock is considered as two-phase saturated porous media. In order to consider the viscoelastic characteristics of the saturated site soil,the stress-strain relationship of soil skeleton is described by fractional derivative Kelvin viscoelastic model,and the motion control equations of overlying fractional derivative viscoelastic saturated site soil under the action of harmonic earthquake wave are established. Using the properties of fractional derivative and considering the boundary conditions and permeable conditions,the vibration problem of overlying fractional derivative viscoelastic saturated site soil under the action of harmonic earthquake wave is solved,and the seismic displacement amplification coefficient of the saturated site soil is also obtained. The influences of the order of fractional derivative,liquid and solid coupling coefficient,model parameters of soil,and bedrock and soil shear modulus ratio on the seismic displacement amplification coefficient are analyzed and discussed by numerical examples. The results show that the order of fractional derivative,liquid and coupling coefficient,model parameters of soil,bedrock and soil shear modulus ratio have great effects on the seismic response of the site soil. The fluid and solid coupling coefficient could the increa of be increased and the seismic response can be decreased by compacting the saturated soil. Meanwhile,the viscosity and shear modulus of the saturated site soil can also reduce the seismic response.
saturated soil; fractional derivative; seismic wave; seismic amplification coefficient; fluid and soil coupling coefficient
10.11835/j.issn.1674-4764.2015.05.007
2015-07-16 基金項目:國家自然科學基金(U1504505);河南省科技發展計劃項目(142102210063);河南省高等學校重點科研項目(15A560036);河南省高等學校青年骨干教師資助計劃項目(2013GGJS-121);信陽師范學院重大課題預研項目(2013ZDYY19);信陽師范學院青年科研基金項目(2014-QN-063);信陽師范學院青年骨干教師資助計劃(2012007)。
劉林超(1979-),副教授,博士,主要從事多孔介質理論、粘彈性理論、樁基動力學研究,(E-mail)llc109@126.com。
Foundation item:National Natural Science Foundation of China(No.U1504505); Development of Science and Technology Plan Project of Henan Province(No.142102210063); Key Scientific Research Project of Henan Province(15A560036); Youth Backbone Teacher Plan Project of Colleges and Universities in Henan Province(2013GGJS-121); Major Beforehand Research Project of Xinyang Normal University(2013ZDYY19); Scientific Research Fund for Young of Xinyang Normal University(2014-QN-063); Youth Backbone Teacher Plan Project of Xinyang Normal University(2012007).
TU573.12
A
1674-4764(2015)05-0048-06
Received:2015-07-16
Author brief:Liu Linchao(1979-),associate professor,PHD,main research interests: theory of porous medium,viscoelastic theory,pile dynamics,(E-mail) llc109@126.com.

